异侧竖缝式鱼道在某工程的数值模拟与分析

李 洋，韩 雷，李树航，田振华，狄高健，苏国青

(1.黑龙江省水利科学研究院，黑龙江 哈尔滨 150080；2.黑龙江大学 水利电力学院，黑龙江 哈尔滨 150080 )

在水利工程建设过程中，由于人为截断水流，迫使具有洄游习性的鱼类无法繁衍，导致鱼类的减少甚至是某种鱼类的灭绝，因而建立一些过鱼工程设施帮助鱼类洄游繁衍非常有必要。目前应用最广的水利工程设施就是鱼道，鱼道按结构形式可分为水池式、隔板式，隔板式又可分为溢流堰式、淹没孔口式、竖缝式和组合式[1-2]，其中竖缝式鱼道又包括同侧竖缝式鱼道和异侧竖缝式鱼道。竖缝式鱼道可适应较大的水位变幅[2-3]，有利于鱼类的洄游，其在恢复水生物的多样性方面发挥着重要的作用。与同侧式竖缝鱼道相比，异侧竖缝式鱼道其隔板相互交错，具有更好的消能效果，使得池室内最大流速较小。此外，异侧竖缝式鱼道具有较好的主流区水流流态，更有利于鱼类在上溯过程中的休息，便于洄游[3]。

目前国内外对同侧式竖缝鱼道研究较多，对异侧式鱼道研究较少。刘志雄等[1]以3种池室长度和3种竖缝宽度分析池室结构变化对异侧竖缝式鱼道的影响，结果表明池室内水流为二维水流，并确定了主流流速与竖逢平均流速的比值范围。董志勇等[4]以异侧竖缝式鱼道为研究对象，通过研究2种流量3种水深下的水力特性，提出主流轨迹的经验公式、主流速度沿程变化的关系式和横向流速分布特征的半理论半经验公式。曹庆磊等[3]利用三维超声波流速仪量测了异侧竖缝式鱼道中的流速，并对不同流量不同水深的流速场、稳动能以及应力进行了分析，结果表明鱼道池室中流速沿着垂向的分量很小，几乎为零。张羽等[5]利用数值模拟方法分析了不同竖缝宽度下池室水流结构、流速分布和回流区分布的变化情况。对于池室底坡坡比对池室水力特性的影响仅有少数国内外学者进行了研究，加拿大学者Wu等[6]首次通过以池室长宽比、水池底坡坡度为变量对竖缝式鱼道的水力特性进行了比较系统的试验研究，给出了鱼道过流流量的经验公式。Mao等[7]研究底孔和水池底坡坡度对鱼道内流速和流型等水力特性的影响。

国内外学者对于底坡坡比和池室长宽比对池室水力特性进行了系统的研究，但没有针对特定工程的具体鱼类进行分析，刘志雄只选取了三种池室长度探究池室结构变化对鱼道水力特性的影响，参数变化范围较小，借鉴前人的研究成果研究池室内水流为二维流，池室中垂向流速进分量较小，本文选取5种底坡坡比，7种不同池室长宽比探究池室结构变化对池室水力特性的影响，研究内容包括池室主流区平面水流形态、池室主流区最大流速沿程分布、回流区面积以及回流区流速分布，从而得到不同底坡坡比、不同池室长宽比组合情况下的普遍规律，并提出适合研究区域鱼类的底坡坡比和池室长宽比，并为其它类似异侧竖缝式鱼道工程的设计提供参考依据。

1 研究区概况及鱼道池室结构设计

枢纽工程由混凝土溢流坝、冲沙闸、城市供水闸、隔板式鱼道组成。鱼道布置在枢纽右岸，鱼道紧贴溢流坝，边墙兼做溢流坝导墙，鱼道采用U型槽结构设计。枢纽工程鱼道过鱼保护对象主要是哲罗鲑及四大家鱼。国内部分单位进行了四大家鱼的克流能力测试试验，积累了一些相关结论和资料，根据过鱼种类及其克流能力，研究区域内鱼类的感应流速取0.2 m/s，极限流速为1.2 m/s，极限流速是鱼类克服困难上溯成功的最大流速，鱼道内的最大流速不能超过鱼类的极限流速[8]，鱼道设计流速建议为1.2 m/s。

鱼道总长42 m，池室宽度B=3 m，长隔板长2 m，横向导板P=1 m，竖缝宽度b=0.46 m。由文献可知，当竖缝位置距离池室边壁在25%～35%之间(横向导板长度P与池室宽度B之比)[9]、竖缝宽度与池室宽度之比(b/B)在0.10～0.25之间[6]、鱼道各级水池的池室长宽比(L/B)在1.2～1.5之间[8,10-13]时，鱼道池室内可获得较为理想的水流流态，本次设计P/B=0.33、b/B=0.153，通过更改池室长度调节变量池室长宽比。池室长度L分别选取2.0 m、2.5 m、3.0 m、3.5 m、4.0 m、4.5 m、5.0 m，对应池室长宽比(L/B)分别为0.67、0.83、1.00、1.17、1.33、1.50、1.67，其中池室长宽比为1.17、1.33、1.50、1.67时满足设计要求，但有时实际工程受地形条件、建设费用、施工难度的影响，池室长宽比偏小，主流区最大流速轨迹线曲率半径较小，不利于鱼类洄游[14]，因而选取池室长宽比为0.67、0.83、1.00进行水力特性的研究，为受地形等因素影响较大，采用池室小长宽比的工程应用提供参考。大底坡坡比鱼道池室内最大流速一般较大，需要不断优化池室内部尺寸来降低流速，使其低至鱼类的极限流速。国内外大部分鱼道的应用的底坡坡比设计均为小底坡坡比，本文选取的坡比(i)分别为1∶50、1∶60、1∶70、1∶80、1∶90。鱼道池室结构设计见图1。

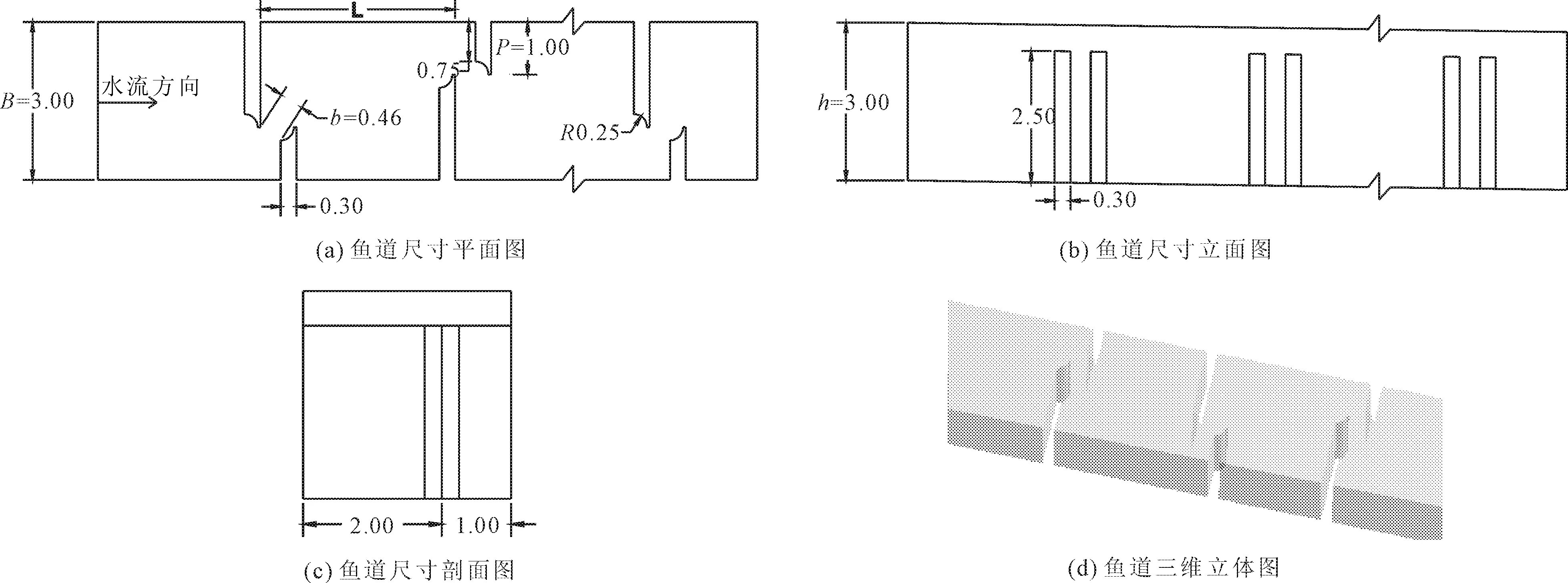
图1 鱼道尺寸布置(单位：m)

2 基本控制方程

鱼道采用专业软件Fluent中标准K-ε模型并耦合VOF模块对水流自由表面进行捕捉[13,15-16]；其中三维水流模型的控制方程如下：

连续方程：

(1)

动量方程：

(2a)

(2b)

(2c)

标准k-ε紊流模型方程：

(3)

(4)

其中紊动能：

(5)

紊动黏性系数：

(6)

式中：ρ为密度；u、v和w是速度矢量在x、y和z方向的分量；t为时间；μ为动力黏度；p为流体微元体上的压力；Su、Sv和Sw是动量守恒方程的广义源项；k为紊动能；ui为时均速度；μt为紊动黏度；模型常数Cμ= 0.0845，C1ε=1.44，C2ε=1.92，σk=1.0，σε=1.3；Gk为平均速度梯度引起的紊动能产生项；ε为紊动能耗散率。迭代计算的各项残差值均为10-5，时间步长设置0.01 s[5]，在模型验证时，在时间步数15 000内，计算结果就已经收敛，因而在后面各工况计算时，时间步数设置较长为20 000。

3 模型建立以及模型验证

3.1 网格剖分以及边界条件

数值模拟选取鱼道长度与物理模型试验原长一致，为42 m。网格最大边长尺寸为0.05 m，最小边长尺寸为0.1 m，均为规则六面体，其中节点2 711 885个，网格2 580 822个，见图2(a)。

图2 鱼道网格剖分

为便于看清具体网格分布情况，对局部网格进行放大处理，见图2(b)。

将鱼道数学模型上游边界设置为流量进口，流量为0.94 m3/s；将鱼道数学模型下游边界设置为水深和压力出口，水深为2 m，压强为1个大气压；顶部设置为气体压力进口，压强为1个大气压，边墙以及底部设置为无滑移固壁边界。

追踪自由液体表面采用VOF方法，通过计算水和气的体积分数来表征物体的形态，其控制方程如下：

aw+aa=1

(7)

(8)

其中:aa表示气体的体积分数，aw表示水的体积分数。

3.2 模型验证

为了验证数学模型参数设定的合理性以及网格剖分的正确性，对鱼道进行物理模型验证试验[14]。验证内容为4-5池室主流区沿程最大流速曲线及2号隔板到9号隔板竖缝附近最大流速(水流进口的1号隔板处和10号隔板竖缝附近最大流速受到干扰严重，不对两处最大流速进行测量，流速通过无线旋浆流速仪测定)。试验采用有机玻璃以1∶5的比尺制作鱼道模型，坡比为1∶70，池室长度为0.74 m(对应原型的池室长度为3.7 m)，该模型全长42 m，内设10组隔板，具体见图3。有机玻璃糙率为0.009，对应原型的糙率为0.012，与实际工程中鱼道混凝土糙率略有差别。考虑到鱼道中除了竖缝断面处水流流速较大外，各级水池边界处的水流流速通常都较小，边壁的沿程摩阻不大，水头损失主要集中在竖缝断面附近的局部区域，因而原型与模型糙率不相似所导致的的比尺效应对试验结果的影响可以忽略。模型测点布置见图4，以左下角为测定原点，沿着水流方向为X轴，垂直水流方向为Y轴，沿着水流方向每6 cm(对应原型为0.3 m)布置一个测量断面，断面共计13个，每个断面布置13个测点，测点间距为5 cm(对应原型距离为0.25 m)，流速测量点共计169个，测量模型水深为4 cm，对应原型水深为0.2 m，选取每个断面最大流速与数值模拟进行对比拟合，拟合结果见图5(a)，2号～9号隔板竖缝附近最大流速实测和数值模拟拟合情况见图5(b)。

图3 物理模型装置

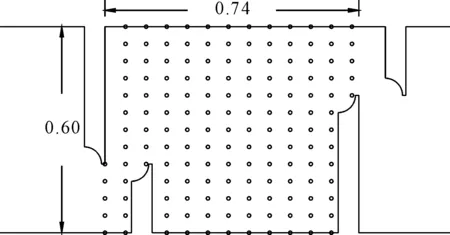
图4 测点分布(单位：m/s)

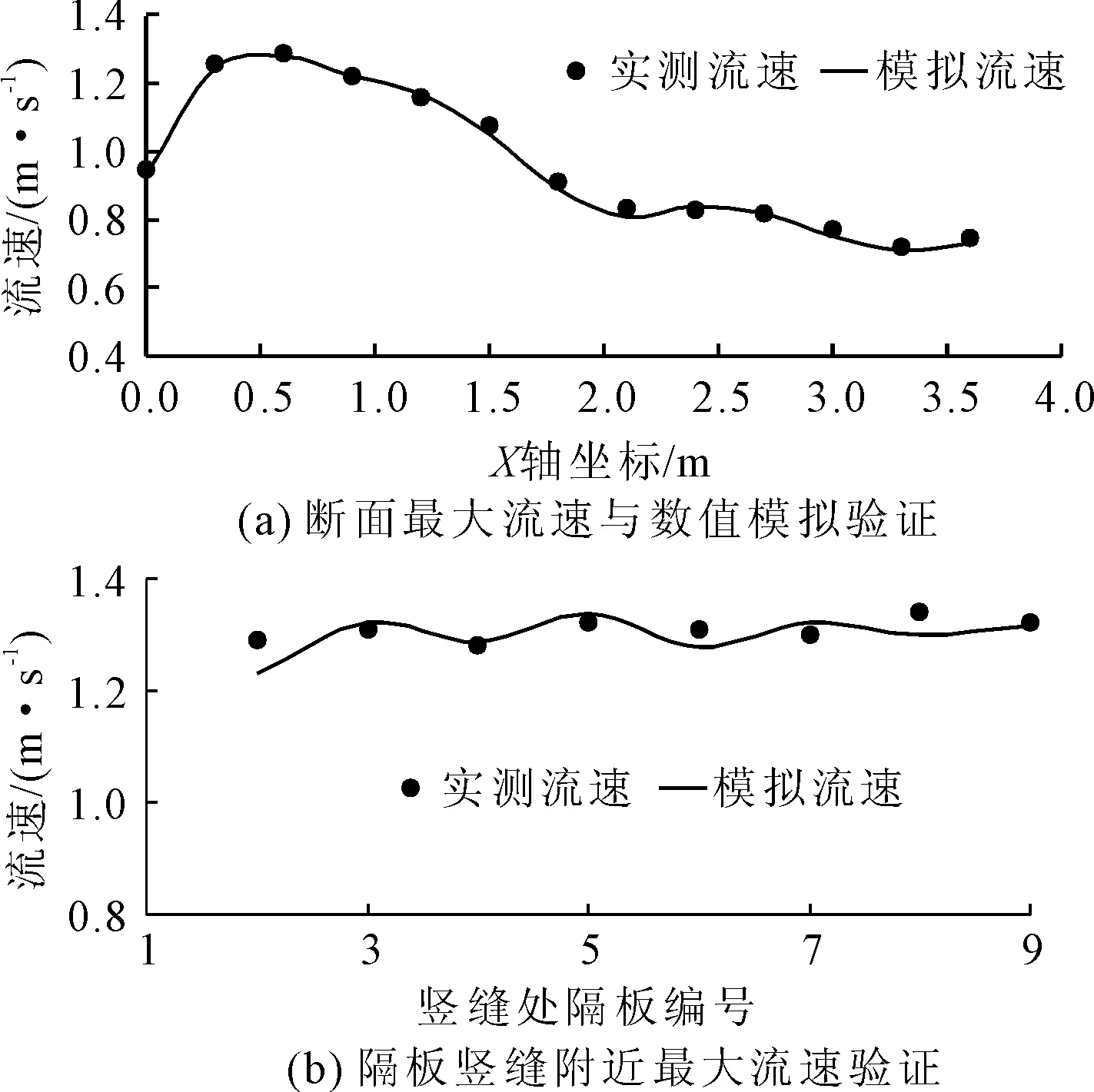
图5 数据拟合模型验证

从图5(a)中可以看出，物理模型测量的最大流速位置距离原点0.4 m，最大流速为1.29 m/s；数值模拟最大流速距离原点0.4 m，与物理模型测量的结果一致，最大流速为1.294 m/s，略大于实测值。数值模拟主流区沿程最大流速曲线分布规律与物理模型实测流速分布规律基本吻合，拟合误差仅在0.1%～3.0%范围内；从图5(b)中可以发现，隔板竖缝附近最大流速实测值与数值模拟值误差范围在0.3%～5.0%范围内，说明数值模拟参数设置正确，网格剖分合理。此时数值模拟所设的糙率为0.0136，在后面的数值模拟过程中糙率保持不变。

4 池室水力特性分析

4.1 主流区平面形态分析

主流区的弯曲程度影响着水流形态，进而影响着鱼类的洄游效果，主流区平面形态呈现S型是竖缝式鱼道的特点，因而探讨主流区平面形态是很有必要的。对验证后的数学模型进行数值模拟，选取35种不同组合型式的池室进行模拟计算，模拟结果较多，因而只列出2种底坡坡比和3种池室长宽比的模拟结果，详见图6。

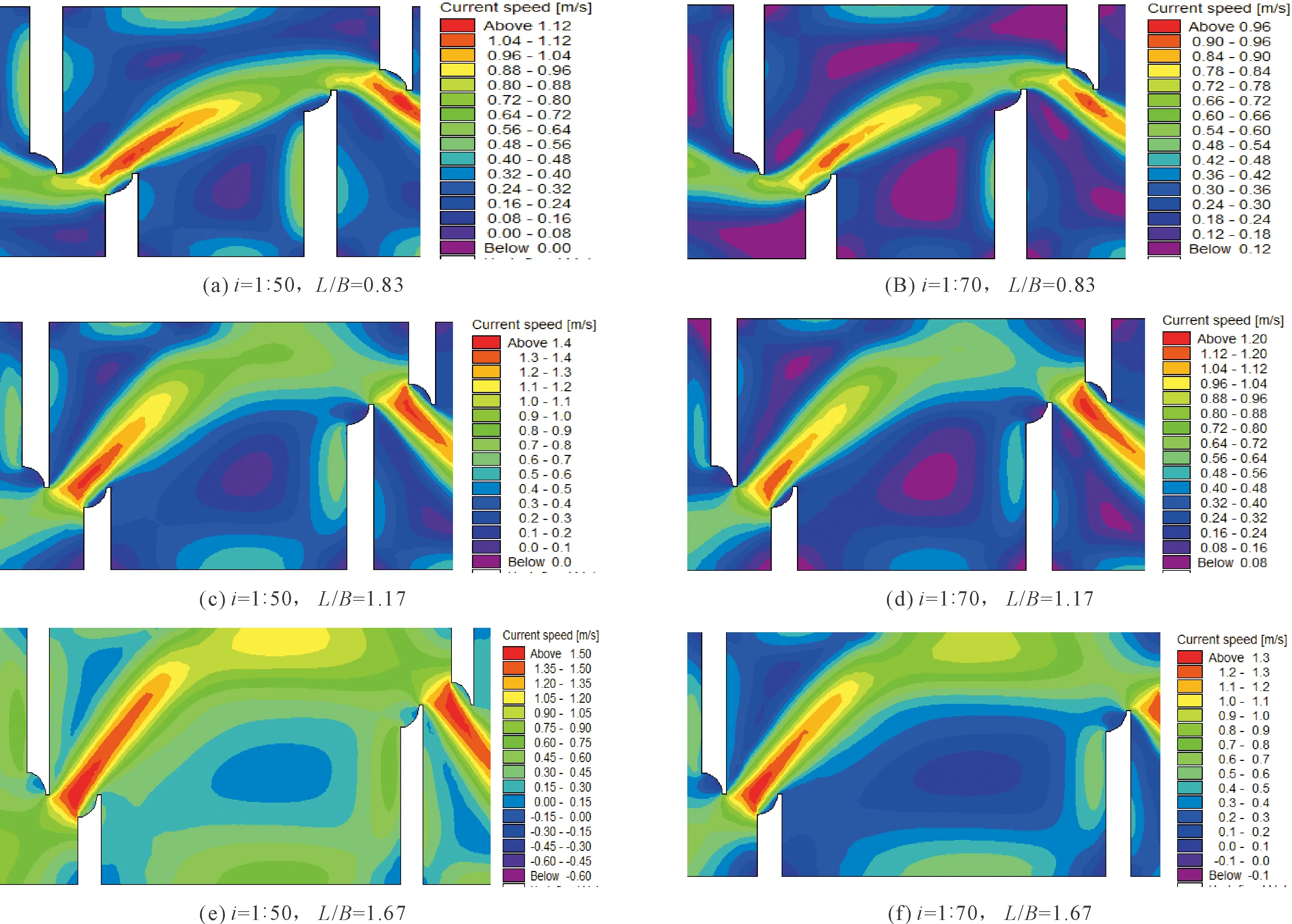
图6 不同底坡坡比不同池室长宽比流速分布

由数值模拟结果可知，各底坡坡比各池室长宽比相邻池室主流区平面形态均呈现出S型，池室长宽比越大S型越明显，而同侧竖缝式鱼道单独池室主流区平面形态便呈现S型[2,17]。但是在各底坡坡比、池室长宽比为0.66、0.83时，相邻两级池室隔板间主流区平面形态弯曲较大，曲率半径较小，主要是因为小长宽比下，相邻两隔板距离较近，经过上一个竖缝的水体来不及与池室水体充分混合，便迅速进入下一竖缝。同时可以看出主流区平面形态分布规律与底坡坡比无关，即池室长宽比确定后，主流区平面形态不随着底坡坡比的变化而发生改变。

当池室长宽比L/B>0.83，相邻主流区平面形态衔接较平顺，更有利于研究区域鱼类发现洄游通道并上溯。

4.2 主流区最大流速沿程曲线

主流区最大流速沿程曲线为池室内每一断面流速最大值点所在的曲线[17-18]，根据数值模拟得到各底坡坡比各池室长宽比的各横断面沿程最大流速曲线，详见图7。

图7 不同底坡坡比不同池室长宽比(池室长度)最大流速分布

从沿程最大流速曲线可以得到如下结论：

(1) 各种组合下沿程最大流速曲线呈S型。在池室长宽比确定后，底坡坡比的变化不改变沿程最大流速的分布，只影响各断面的最大流速，主要是因为竖缝位置相同，竖缝射流效果相同，因而沿程最大流速曲线相同，但坡比越大，相同位置流速越大。

(2) 在各池室长宽比确定下，沿程最大流速曲线分布规律相似，池室小长宽比下，如图7(a)，沿着水流方向出现两次波峰和两次波谷，主要是因为小长宽比下，主流区水体进入竖缝时，还没有充分消能，导致流速降低到第一次波谷，后经过竖缝束窄，流速开始增加，在距离竖缝0.6 m时沿程流速达到波峰，后主流区水体与池室水体充分混合扩散，流速降低到第二次波谷，快到下一竖缝时，流速又增加到第二次波峰；而在较大池室长宽比下，如图7(d)，出现一次波峰和两次波谷，主要是因为主流区水体进入竖缝时主流区水体已经充分消能，进入竖缝束窄时流速一直在增加，在距离竖缝0.4 m流速达到波峰，后又充分消能，在距离竖缝2 m时，出现第一次波谷，经过扩散出现第二次波谷，后经过下一竖缝流速开始增加。

(3) 同底坡坡比时，各横断面最大流速与池室最大流速(各横断面出现的最大流速的最大值)比值在0.55～1.00之间，各横断面最大流速均超过池室最大流速的1/2，因而测量出池室最大流速就可了解主流区流速沿程变化规律；池室长宽比越大，池室最大流速越靠近竖缝处(图7(a)、图7(b)红色线)，主要是池室长宽比越大，在进入竖缝前主流区水体已经充分消能，束窄后流速快速增加到最大值。

对5种底坡坡比各池室长宽比池室最大流速进行整理，见表1。

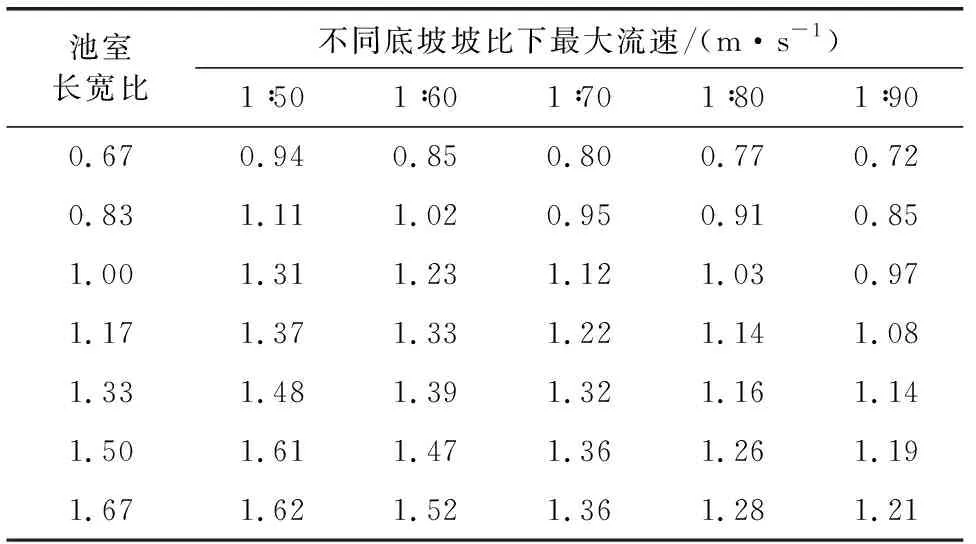
表1 各底坡坡比不同池室长宽比池室最大流速表

由表1可知，池室长宽比与底坡坡比越大，池室最大流速越大，主要是因为坡比越大，重力势能转换为动力势能越大，同时沿程水头损失越小。本次鱼道设计流速为1.2 m/s，在i=1∶50，L/B=0.67、0.83时；i=1∶60，L/B=0.67、0.83；i=1∶70，L/B=0.67、0.83、1.00时；i=1∶80，L/B=0.67、0.83、1.00、1.17、1.33时;i=1∶90，L/B=0.67、0.83、1.00、1.17、1.33、1.50时，池室最大流速符合设计要求。

不同底坡坡比不同池室长宽比的沿程最大流速曲线衰减进行分析见表2，其中umin为各横断面上的最大流速的波谷值，umax为各横断面上的流速最大值的波峰值[12,19-20]。

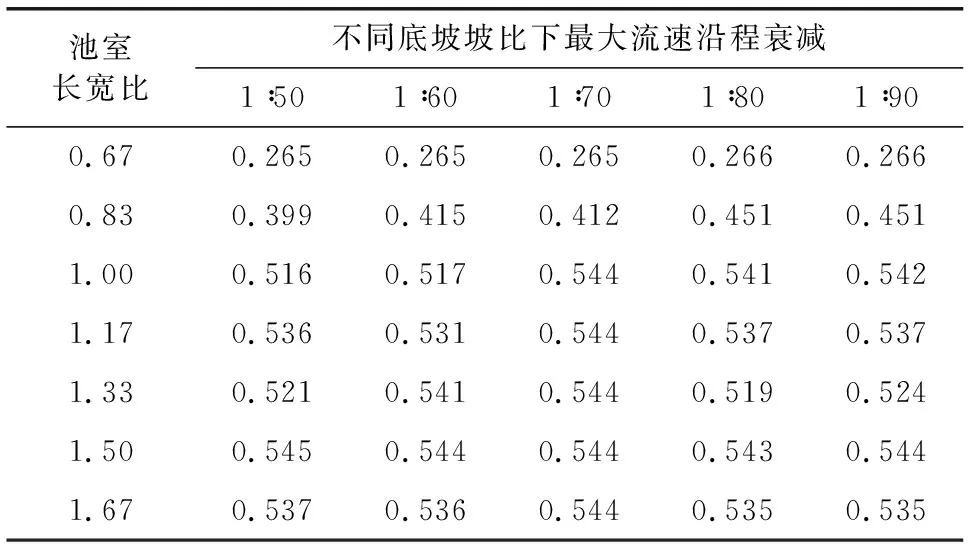
表2 主流区最大流速沿程衰减

一般认为最大流速曲线上流速沿程变化越大，衰减越明显，反映出水池内沿程水头损失越大，消能效果越好，越有利于鱼类上溯[21-22]。由表3可知，同一底坡坡比下，随着池室长宽比的增加，沿程最大流速曲线衰减逐渐增大，当池室长宽比L/B大于1后，衰减率趋于饱和，主要因为此时主流区水体与池室边壁发生碰撞，消能效果好，流速增加缓慢；同一池室长宽比下，底坡坡比对最大流速沿程衰减程度几乎无影响。单从衰减率来看，不用底坡坡比下，池室长宽比L/B=1.0、1.17、1.33、1.50、1.67时衰减率达到最大且处于饱和状态。

从工程过鱼对象考虑，池室内最大流速不应超过设计流速1.2 m/s，同时主流区沿程衰减越明显，消能效果越好，鱼道推荐组合为：i=1∶70时，L/B=1.00；i=1∶80时，L/B=1.00、1.17、1.33；i=1∶90时，L/B=1.00、1.17、1.33、1.50。

4.3 主流区最大流速沿程位置分布

主流区最大流速沿程轨迹线是鱼类上溯的主要路径，本节要对不同底坡坡比和不同池室长宽比最大流速沿程轨迹进行分析，具体最大流速沿程位置分布见图8。

从图6和图8可知：

(1) 同一池室长宽比，主流区最大流速沿程位置不随着底坡坡比的变化而发生改变。同一底坡坡比下，随着池室长宽比增加，主流区最大流速分布位置随之延长，主流区最大流速沿程位置也越向池室边壁靠拢，平行水流部分与池室边壁最小距离为呈现减小趋势。各底坡坡比条件下，随着池室长宽比的增加，最小距离从池室长宽比为0.67(L=2 m)时的0.825 m减小到池室长宽比为1.67(L=5 m)时的0.225 m；平行水流部分的长度随着池室长宽比的增加而增加，当池室长宽比从0.67增至1.67(L=2 m～5.0 m)时，平行水流长度相应地从0 m增至2.3 m，因为当池室长宽比较小时，相邻竖缝距离较小，通过上一竖缝的水体还没得及和池室水体充分混合，便迅速进入下一竖缝处；当池室长宽比越大，相邻竖缝距离越大，竖缝射流作用相互影响越小，距离竖缝远处的主流区水体可以与池室水体相互充分混合。

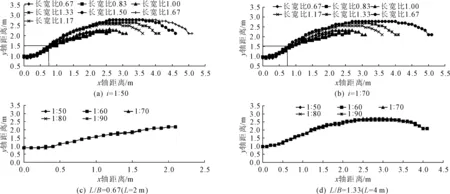
图8 不同底坡坡比不同池室长宽比(池室长度)最大流速沿程位置分布

(2) 各底坡坡比各池室长宽比，在X轴方向距离坐标原点0.8 m，在Y轴方向距离坐标原点1.5 m范围内(图8(a)、图8(b)红线范围内)，不同断面最大流速值沿着水流方向均呈现增加趋势，但最大流速的位置未有明显变化，主要是因为距离竖缝较近处，射流效果相同，当远离竖缝时，池室长宽比越大，射流效果越弱。

4.4 回流区水力特性分析

回流区的面积大小和流速分布影响着鱼类的上溯过程中的休息，本节主要回流区的水力特性进行分析。回流区流速等值线图和流速矢量图见图9(a)和图9(b)，不同底坡坡比、不同池室长宽比的回流区最大流速分布见图9(c)和图9(d)。

对回流区水力特性进行分析可知：

(1) 池室内部存在两个回流区，即靠近上游隔板回流区和靠近下游隔板回流区。随着池室长宽比的增加，靠近上游隔板回流区面积逐渐变小，靠近下游隔板回流区面积逐渐增大。当L/B=0.67、0.83时，靠近上游隔板回流区的面积大于靠近下游隔板回流的区面积；当池室长宽比为1时，两侧回流区面积大致相等；当L/B=1.17、1.33、1.50、1.67时靠近上游隔板回流区的面积小于靠近下游隔板回流区的面积。

(2) 靠近上游隔板回流区和靠近下游隔板回流区均包括两个较大流速区，靠近上游隔板回流区最大流速区出现在左侧边壁处(图9(a)红圈处)，较小流速区在水流进口隔板处(图9(a)黄圈处)；靠近下游隔板回流区最大流速区出现在隔板边壁处(图9(a)粉圈处)，较小流速区在右侧边壁处(图9(a)绿圈处)。两个回流区的中心流速都比较小。

(3) 上游隔板回流区附近最大流速区的最大流速一直小于靠近下游隔板回流区最大流速区流速。由于篇幅原因，只列出i=1∶70两个回流区的最大流速分布如图9(c)所示。对不同底坡坡比不同池室长宽比的回流区最大流速进行处理如图9(d)。可以发现，相同底坡坡比条件下，回流区最大流速先是随着池室长宽比的增加而增加，当池室长宽比增加到1.17时出现贴壁流现象，回流区最大流速基本不再发生变化。以i=1∶70为例，L/B=0.67，回流区最大流速0.37 m/s；L/B=0.83，回流区最大流速0.5 m/s；L/B=1.00，最大流速0.56 m/s；L/B=1.17、1.33、1.50、1.67时回流区最大流速均在0.59 m/s左右。相同池室长宽比时，底坡坡比越大，回流区流速越大。相同坡比下，各长宽比池室的回流区最大流速与池室最大流速比值均在0.40～0.53之间。

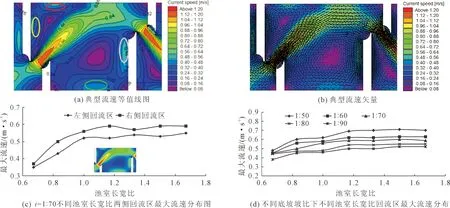
图9 回流区水力特性分布

(4) 当L/B=0.67、0.83、1.00时，靠近上游隔板回流区面积大于靠近下游隔板回流区面积，但二者面积相差较小，在任意回流区内鱼类都可以很好的休息；当L/B≥1.17时主流区出现贴壁流现象，会使上溯的鱼类造成伤害，因而池室长宽比宜在0.67～1.00之间，此工程池室长宽比L/B可选为1.00。

5 结 论

本文采用数值模拟方法对不同底坡坡比、不同池室长宽比下的鱼道的水力特性进行了分析，结论如下：

(1) 当池室长宽比确定后，不同底坡坡比只影响沿程最大流速大小，不影响主流区最大流速沿程分布；当底坡坡比确定后，池室长宽比变化对主流区最大流速沿程分布、位置分布、最大流速沿程衰减都有影响。

(2) 池室长宽比不断增加，池室最大流速位置越靠近竖缝处。由于竖缝射流的影响，即使是在不同底坡坡比不同池室长宽比下，距离竖缝位置一定范围内，沿程最大流速位置并未改变。

(3) 对于研究区内的鱼道参数设计，从主流区平面形态分析，不同池室坡比下，当L/B=1.00、1.17、1.33、1.50、1.67时，相邻两级池室隔板间主流区平面形态弯曲较小，研究区域内鱼类在上溯过程中更容易识别通道；当L/B=0.67、0.83、1.00时，回流区两侧面积相差较小且池室主流区未出现贴壁流现象，研究区域内鱼类在上溯过程中不会受到伤害；当L/B=1.00、1.17、1.33、1.50、1.67时，池室最大流速沿程衰减率基本一致，且都达到最大值，消能效果较好。

(4) 由于鱼道设计流速为1.2 m/s，故池室内最大流速不能超过1.2 m/s，考虑到相邻两级池室隔板间主流区平面形态以及主流区贴壁流现象，池室长宽比L/B宜选为1.00(池室长度L宜为3.0 m)，坡比i宜选为1∶70、1∶80、1∶90。