基于BAS-BA优化BP神经网络的轴承故障诊断方法*

晏生莲 巩永旺 潘琳鑫

（盐城工学院信息工程学院 盐城 224051）

1 引言

滚动轴承是机械设备中最常用的机械零件，也是最易磨损的零件之一，关乎到机械生产过程中的安全。因此如何实现轴承故障的快速准确诊断长期受到人们的关注。常规轴承的故障诊断方法一般有振动信号法、温度分析法、声辐射法、光纤检测法等［1］。在这些方法中，振动信号法是最常用的。但由于滚动轴承的失效影响因素比较复杂，这些常规的故障诊断方法容易出现误诊，严重地影响了故障诊断的精度。

随着人工智能技术的发展，人们利用多种智能算法对轴承故障的诊断问题进行了分析研究［2～3］。作为最成功的神经网络之一，BP神经网络具有很强的非线性映射和适应性，常用于解决各领域复杂的非线性问题［4～6］。BP神经网络的学习规则是通过最速下降法来确定误差函数的最优值，这种方法使得BP网络存在学习算法收敛缓慢，难以判断隐层结点数目，网络泛化能力差［7］等问题。近年来，随着智能算法的发展，将BP神经网络与智能算法结合起来，以优化权值和阈值得到了越来越多的研究者的认可，并提出了众多的改进算法［8～9］。例如，蝙蝠算法［10］（Bat Algorithm，BA）作为一种基于仿生优化算法的全局最优搜索方法，模拟蝙蝠种群，在解空间中进行最佳搜索，获得全局最优值，算法简单、收敛速度快，极大地改善了BP神经网络的缺点，然而，在迭代的后期，蝙蝠算法往往会陷入局部最优，这对种群的多样性产生一定的影响。天牛须算法（Beetle Antennae Search，BAS）［11］是一种新型智能优化算法，参数少、计算量小，凭借其在个体查找局部最优方面具有优势，常被运用于其他智能算法的优化问题中［12～13］。文献［14］将BAS和BA进行混合（Beetle Antennae Search Bat Algorithm，BAS-BA算法），弥补了BAS算法在全局寻优上以及BA算法在局部寻优上存在的不足，提高了算法收敛速度和稳定性。

基于文献［14］的研究，本文将BAS-BA算法用于优化BP神经网络的初始权值和阈值，提出一种基于BAS-BA算法优化BP神经网络并应用于轴承故障诊断。基于凯斯西储大学轴承数据集进行仿真实验，结果表明，BAS-BA算法优化的BP神经网络在收敛能力和轴承故障诊断准确率方面均优于单个算法（BAS或BA）优化的BP神经网络。

2 BP神经网络

BP神经网络模型［15］是一种较为成熟且应用广泛的神经网络模型，相对其他传统模型而言，BP神经网络的输入层、隐藏层和输出层的三层模型结构（见图1）具有较好的持久性、适时预报性和分类能力。核心算法过程分成两个部分：正向和逆向传递。在正向传递过程中，信号由输入层向隐含层传递，经过隐含层的处理后，再向输出层传递，各层中的神经元状态只对下一层的神经元状态产生影响。如果输出层接收到的信号误差超出了误差门限，则转入反向传播，并沿着原来的神经元连接路径返回误差信号。在返回的过程中，网络对各连接层神经元的权重和阈值进行修正。重复迭代以上过程，使得信号误差能够达到允许的误差范围，网络模型趋于最优化。

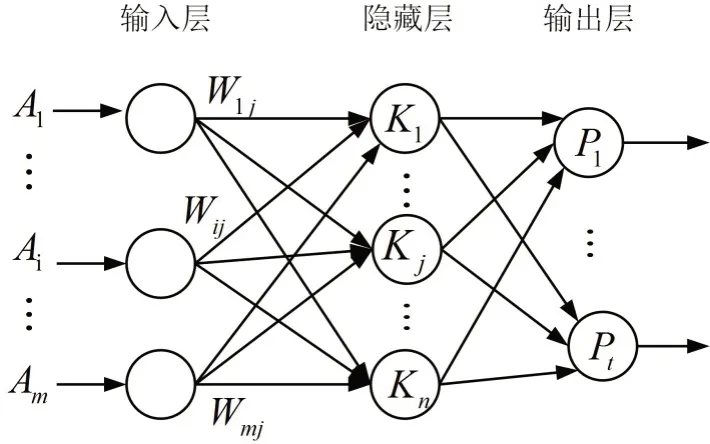
图1 典型的三层BP神经网络结构

其中A1,A2,…,Ai,…,Am为输入层神经元的输入，W1j,W2j,…,Wij,…,Wmj为输入层第i个节点与隐藏层第j个节点之间的网络权重，K1,K2,…,Kj,…,Kn为隐藏层输入，P1,P2,…,Pt为输出层输出。

3 天牛须和蝙蝠混合算法

3.1 蝙蝠算法BA

蝙蝠算法［16］是根据蝙蝠的觅食过程进行位置优化的，蝙蝠在早期阶段发出大响度的脉冲，以便在捕猎时寻找猎物，当它快要接近猎物的时候，它会降低脉冲的声音来捕捉猎物，其步骤如下。

第一步：初始化蝙蝠的种群规模size，响度Ai，脉冲发射率ri，以及最大迭代次数T，最大和最小的脉冲频率fmax和fmin，计算初始种群中蝙蝠适应度值，选择最优个体x*。

第二步：全局搜索，根据位置、速度更新公式对参数进行更新。

其中，α为随机数，在［0，1］上均匀分布，和分别表示第i只蝙蝠在第t+1代时的速度和位置。

第三步：局部搜索，生成随机数R1、R2，若R1＜ri，接受新解，否则随机飞行产生新解），若R2＜Ai且新解更优，则选择接受新解，调整ri、Ai大小，否则转向局部搜索，更新种群最优速度和位置，Ai、ri调整算法如式（3）和式（4）所示：

其中xnew表示新解服从均匀分布，ε,γ为常数，At是t时刻所有蝙蝠的平均响度。

第四步：比较当前所有蝙蝠的适应度值，得到当前最优解x*。

第五步：判断是否满足终止条件，若满足则输出最优解，否则继续迭代，直至满足终止条件。

3.2 天牛须算法BAS

作为解决优化问题的算法，BAS算法［17］受自然启发，模仿天牛的自然觅食行为。天牛在觅食过程中，天牛的移动方向是由两只触角嗅到目标气味的浓度决定，哪边目标气味更浓，就向哪一边移动，否则就会转向另一边搜索猎物，逐步接近搜索目标，多次迭代，最终确定目标的位置。

在N维空间中，天牛第t时刻的位置为矢量Xt，其中t={1,2,3,…M}，M为迭代次数，则天牛左右两只触角的位置为

其中，和分别表示第t时刻天牛须的左右须位置，l表示天牛质心与触须之间的距离，表示随机单位向量。根据两须嗅到的目标气味的浓度的不同，来判断天牛下一步前进位置：

其中，f(x)为适应度函数，δt表示第t次迭代时的搜索步长，sign(x)为符号函数，η代表步长因子，一般取0.95。

3.3 BAS-BA混合算法

基于天牛须算法思想的改进蝙蝠算法能够帮助群体中的每一个蝙蝠增加搜寻过程中的搜索次数或搜索方向，显著提高全局搜索功能，从而使整体优化算法的精确度得到了极大的提高，有更多机会求解全局最优解，且不易陷入局部最优。算法步骤如下［14］。

第一步：初始化种群大小、搜索范围，响度、脉冲频率和初始步长，种群的位置与速度。

第二步：记录初始最优位置，对最优位置的蝙蝠进行局部搜索，根据天牛须更新公式更新蝙蝠种群的全局最优位置，改进后的种群位置更新公式如下：

第三步：根据BA算法中的局部搜索步骤，对全局最优位置处的个体进行局部最优搜索，比较个体位置优劣和响度大小以更新位置和新解，将该结果和算法第二步中的新位置与最优值进行比较，并使用BAS算法进行全局最优搜索，使天牛个体向最佳位置移动。

第四步：判断是否满足终止条件，若满足则输出最优个体和最优解，否则继续迭代直至满足终止条件。

4 BAS-BA算法优化的BP神经网络模型

将BAS-BA算法用于优化BP神经网络的初始权值和阈值，然后使用优化好的参数对BP神经网络进行训练，提出一个新的故障诊断的BP神经网络模型（记为BAS-BA-BP模型），其原理与步骤如下：

第一步：构建BP网络结构，确定输入层、隐含层和输出层的节点数目，划分训练集样本和测试集样本；

第二步：初始化BAS-BA参数，蝙蝠数目、初始响度，迭代次数和误差精度等；

第三步：计算每个个体的适应度值，寻找当前最优位置；

第四步：根据BAS-BA算法中的第四步和第五步，判断是否更新当前最优解；

第五步：重复迭代，直到达到最大迭代次数或者BP神经网络设定的误差，输出最终的权值和阈值，对BP神经网络进行训练；

In conclusion, the compliance of the Attikon University General Hospital personnel with a FIT-based CRC screening program was suboptimal, especially among physicians, despite the well-organized, guided and supervised provision of the service.

第六步：将测试集样本输入训练好的BP神经网络，得出输出数据，计算均方误差MSE作为三种算法的评价指标，分析结果。

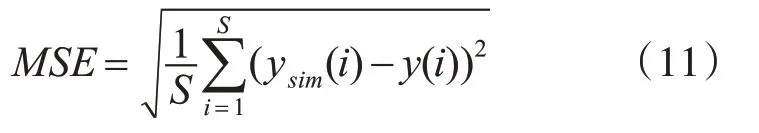
其中S表示输出样本的维度，ysim(i)代表给定样本的第i维的仿真输出结果，y(i)代表给定样本的第i维的期望输出结果。

BAS-BA-BP神经网络流程如图2所示。其中右边虚线框内是BAS-BA混合算法流程，输出的最优解作为BP神经网络的初始权值和阈值，左边是BP神经网络的训练过程，对模型进行训练，不断迭代，直到找到最优权值和阈值。

图2 BAS-BA-BP模型流程

5 实验与结果分析

5.1 数据集与模型参数设计

为验证BAS-BA算法优化的BP神经网络性能，基于凯斯西储大学的轴承振动数据集进行实验与分析。该数据集包含正常状态、内圈故障、滚动体故障和外圈故障等四种状态数据。

针对轴承的振动特点，采用了基于功率谱特征、小波特征和时频域特征提取的方法，对信号进行处理，提取出正常状态、内圈、滚动体、外圈等故障信号，并对所提取的特征向量进行归一化，将其作为BP神经网络的训练集和测试集。BAS-BA的参数设计如下：算法的最大迭代次数为1000，64个训练集样本，16个测试集样本，蝙蝠种群规模为10，脉冲音强0.25，脉冲频度0.5，最大频率为2，最小频率为0；设置天牛须长为5，初始步长30，每种优化算法独立运行10次作平均。该实验通过Matlab 2020b软件构建3层结构的BP神经网络，具体每层节点数见表1。神经网络参数设置为训练次数100次，学习率0.1，目标误差0.00001，其余参数为默认值。

表1 不同特征下BP神经网络各层节点数目

5.2 结果比较与分析

三种特征下，针对BAS-BA-BP模型与单个BAS算法和BA算法优化的神经网络（分别记为BAS-BP模型和BA-BP模型）的实验结果如表2所示，MSE值越小表示轴承故障诊断准确率越高。

表2 三种算法优化BP神经网络

由表2可知，在功率谱特征下，BAS-BA-BP模型故障诊断准确率均高于BAS-BP模型和BA-BP模型。在小波特征和时域特征下，可得出相似的结论。另一方面，对比同一种算法在三种不同特征下训练的BP神经网络，其故障诊断准确率不尽相同，但BAS-BA算法的优化能力均是最强的。因此，BAS-BA混合算法优化的BP神经网络提高了轴承故障诊断准确率。

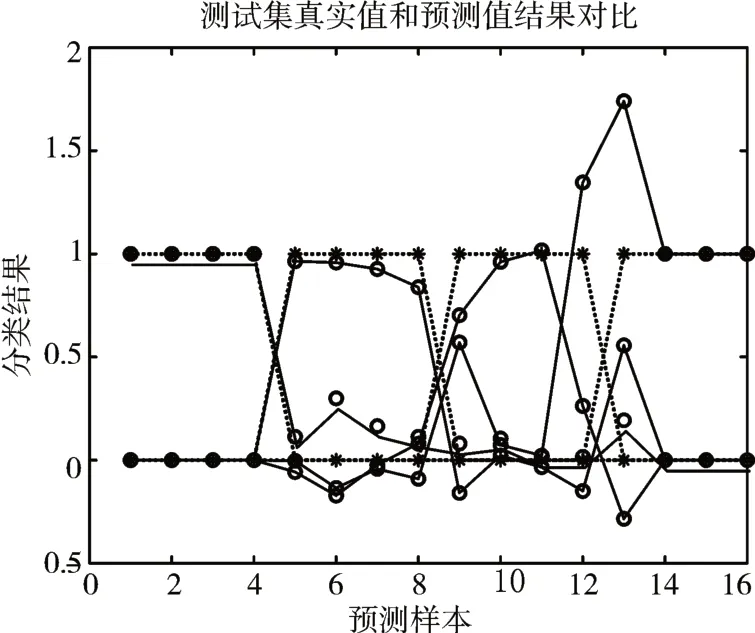
图5 BA-BP真实值和预测值结果对比

由图3可知，BAS-BA算法在迭代到17次的时候已经趋于收敛，而BAS算法和BA算法分别在迭代到44次和57次时才找到全局最优值，说明BAS-BA混合算法的收敛速度更快。为进一步展示三种算法优化BP神经网络下的预测值和真实值之间的逼近程度，在时域频域特征上，分别实验对比了三种模型故障诊断的预测值和真实值如图4～图6所示。其中*表示测试集的真实值，〇表示预测值。重合点表示在此处预测值和真实值一致，重合点数越多，说明该算法下BP神经网络的预测结果准确率越高。显然BAS-BA-BP模型的预测值与真实值逼近效果最好，表示使用BAS-BA优化的BP神经网络轴承故障诊断准确率最高。

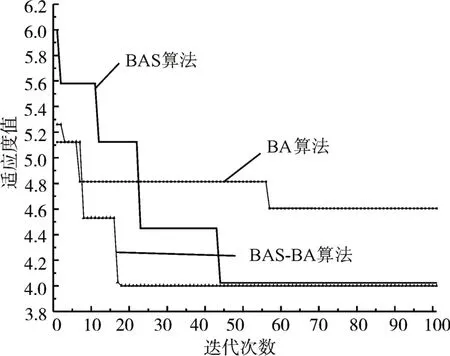
图3 迭代次数和适应度值关系图

图4 BAS-BP真实值和预测值结果对比

图6 BAS-BA-BP真实值和预测值结果对比

表3为轴承故障的四种输出状态与对应坐标。三种算法优化BP神经网络的故障诊断结果如图7所示，其横坐标为测试集样本，纵坐标表示轴承的故障类型。■为真实值，●、▲和▲分别表示BA-BP、BAS-BP和BAS-BA-BP三种模型下的轴承故障的预测值，可更加直观地看出BAS-BA-BP模型的预测值总体上更接近真实值，说明BAS-BA算法优化BP神经网络模型对轴承故障诊断的效果最佳。

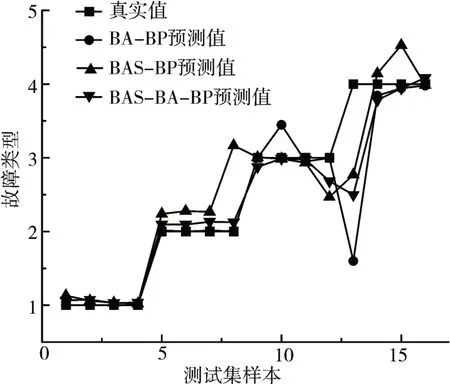
图7 三种模型故障诊断结果

表3 轴承故障输出状态表

6 结语

本文提出一种基于天牛须-蝙蝠算法优化BP神经网络的轴承故障诊断方法，用天牛须-蝙蝠混合算法优化BP神经网络的初始权值和阈值，避免由于系统随机初始化的权值和阈值造成的神经网络效率低下问题，优化初始权值及阈值可以减小训练误差，提高网络的训练速度和精度，最终达到提升轴承故障诊断准确率的目的。将轴承四种状态下的信号分别进行了功率谱分析、小波分析和时频域分析，并将其分别作为BP神经网络的输入，先对BP神经网络进行了参数优化，后将BP神经网络应用到滚动轴承故障诊断中。实验证明，BAS-BA算法优化的BP神经网络方法与其他算法相比，其预测结果与真实结果的误差更小，准确率更高，本方法在实际故障诊断，对轴承等机械设备的可靠性保障、企业的安全生产研究具有一定现实意义。