基于PSO优化ESO的光电稳定平台自抗扰控制*

郑伟伦 夏骏达 王子涵 李 军

（南京理工大学 南京 210094）

1 引言

无人机载光电平台具有多领域、多通道的优势，可对目标实现图像跟踪、红外成像、激光探测等多项监测与集中显示［1～2］，其应用范围越来越广。而无人机在动态情况下所引起的载体姿态变化，会造成光电传感器瞄准线轴指向不稳、图像成像模糊、乃至丢失跟踪目标。为保持平台具有高质量的稳定跟踪能力，采用串联型两轴稳定平台，隔离载体对光电系统的角运动干扰，精确保持光学传感器视轴指向的能力，实现对目标的高精度稳定跟踪［3～4］。

目前主流的稳定平台控制系统仍是以PID控制等经典控制技术为主，但针对于光电稳定平台提出的高精度、高动态的要求，经典PID显得力有未逮［5］。为了保留其不依赖模型和较好稳定性的优点，韩京清院士在提取经典PID的精髓“利用误差来消除误差”，并融入现代控制理论思想，提出了自抗 扰 控 制（Active Disturbance Rejection Control，ADRC）理论［6］。其核心思想为将所有作用于被控对象的不确定因素以及外部扰动都归类为总体扰动，通过扰动观测器对其做出估计并进行总体补偿。因此，自抗扰控制对模型的依赖性进一步下降，其控制精度与动态性能也大大提升［7～8］。但是ADRC引入较多参数且缺乏实用的参数整定方法，因此设计效率较低，控制效果也无法充分体现。而对多目标进行参数优化的算法中，粒子群算法由于其收敛速度、计算效率高、通用性强等优点，被广泛应用于控制器参数寻优之中［9］。

本文针对光电稳定平台对扰动隔离的高精度要求，设计了一种ADRC控制器，针对陀螺反馈信号的时滞问题采用时滞环节的微分预估法，并采用粒子群算法（PSO），动态调整扩张状态观测器（ESO）误差估计系数，实现对参数的自动寻优。

2 光电稳定平台数学模型

本文研究对象为无人机载两轴光电稳定平台，采用直流力矩电机直接驱动，根据陀螺仪检测平台相对空间坐标系的角速度与位置，控制平台稳定，并通过图像得到目标点与实际视轴之间的误差信息，驱动电机稳定跟踪目标。考虑到两轴之间呈正交状态、其耦合扰动较小，可以忽略不计。因此，本文以方位轴控制器设计为例进行说明，俯仰轴控制策略与方位轴类似。

该平台要求在2度1Hz的扰动下，误差精度为1mrad，为保证系统的抗扰性能，本文利用MEMS陀螺，设计了速度与位置的双环控制系统。内环采用积分分离的PI控制器；外环利用四元素解算获得的载体位置信息设计位置稳定环，设计了PSO-ADRC控制器。

由直流力矩电机模型，采用系统辨识的方法获取其电机参数，可得系统模型为

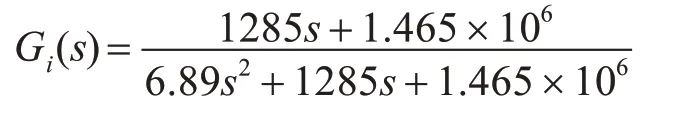
3 自抗扰控制器

本文采用二阶自抗扰控制器，并改变了微分预估器位置，其结构如图1所示。

图1 二阶自抗扰控制器结构图

3.1 时滞环节的微分预估法

在系统控制中，陀螺采样速率达到了1KHz，但在陀螺的硬件之中内置了40Hz的低通滤波器，此外软件的窗口滤波处理、陀螺姿态的四元素法解算，均引入了时滞环节，其总体的时滞相对于本系统1ms的控制周期而言，是不可忽略的，其形式可以记为G(s)e-τs。根据Smith预估原理，可以将被控对象的输出设为θ，预估器输出为θ2，经过预估补偿后的输出为θ0，则有［10］：

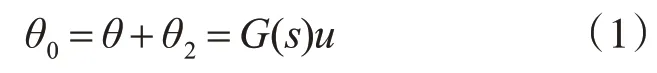
利用一阶泰勒级数将时滞环节展开，然后进行Laplace反变换，可得：

而ADRC算法中，包含了微分跟踪器环节，可由θ求取θ0，并将θ0和u作为观测器ESO的输入信号。考虑到微分跟踪器求解具备滤波功能，可采用微分预估器取代Smith预估，则θ0的算法如下：

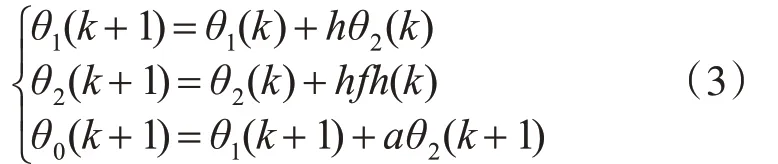
其中θ1≠θ。

3.2 扩张状态观测器ESO的设计

由微分预估得到的系统输出值θ0与控制量u可对系统总扰动进行预估，其表达式为

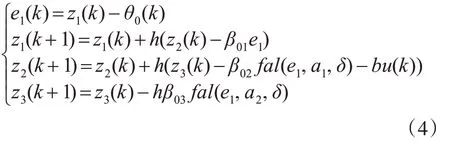
其中：zi(i=1,2,3)为ESO的输出，分别为状态θ1,θ2及 总 扰 动 的 观 测 估 计 值；ESO的 增 益β0i(i=1,2,3)为可调参数；ESO的观测误差为e1(k)，fal(e,ai,δ)为构造的非线性函数。

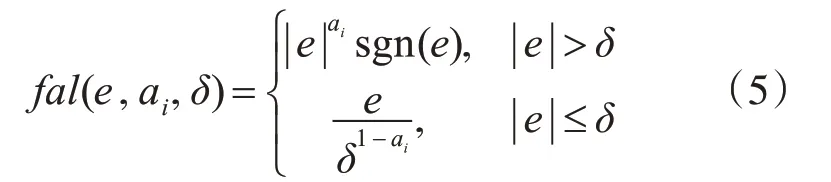
3.3 线性状态误差反馈控制器

经由图像输出作为给定输入，与经过预估分析的反馈信号观测而来的状态量z1,z2形成误差量，将其作为控制器的输入信号。作为串联型系统的一环，这里采用线性控制率达到稳定效果。其控制率为

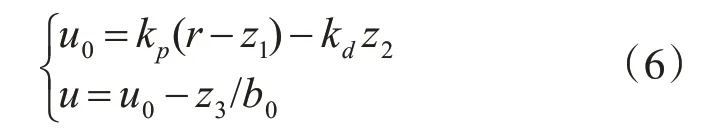
如上所述的ADRC控制器中，微分预估器主要用于克服MEMS陀螺的数据时滞，基本为固定值；而控制器采用了PD控制，可以通过PID调参的方式进行快速整定；扩张状态观测器作为ADRC的核心，包含非线性环节，其参数直接影响扰动观测精度，对系统的抗扰性能影响极大，因此结合改进的粒子群算法，对其扰动估计系数β0i进行在线优化，使“观测”输出信号与“总扰动”信号之间的均方差为最小。

4 改进PSO算法优化的ESO

粒子群算法是一种基于种群的优化算法，其基本思想源于种群中个体之间相互协作与信息共享寻求最优解，具有精度高、收敛快等特性。而且由于其不存在交叉和变异的过程，其运算量大大减小，非常适合在线参数寻优。

图2是采用PSO动态优化的ADRC控制器。PSO优化扩张状态观测器的三个参数β0i，需要利用控制量，并传入预估补偿之后的角位置信息。为了保证优化算法的实时性，对PSO优化条件设定误差阈值。当误差小于阈值时，由ADRC自身的抗扰能力进行稳定控制，不需要PSO优化。当稳定平台扰动较强，误差信号大于设定的阈值，才进入粒子群算法进行实时整定观测器参数［11～12］。

图2 粒子群优化的二阶自抗扰控制器结构图

4.1 适应度函数

采用粒子群算法进行参数寻优，其关键在于适应度函数的选择，直接影响算法的寻优品质。与基于导数信息进行优化的方法相比，PSO算法对适应度函数的要求较低，对其连续性和可微性均无限制，因此设计更为灵活。为了提高观测器的观测精度，综合考虑快速性与稳定性，在均方差指标的基础上，选择常用的适应度函数（ITAE），如式（7）：

其中，e(τ)表示系统反馈值与估计值的误差值，τ时间系数可以保证过渡过程的稳态误差能消除。

4.2 自适应权重

同样PSO算法也存在固有缺陷，其更容易陷入局部最小值，无法收敛至全局最优。其迭代公式如下：

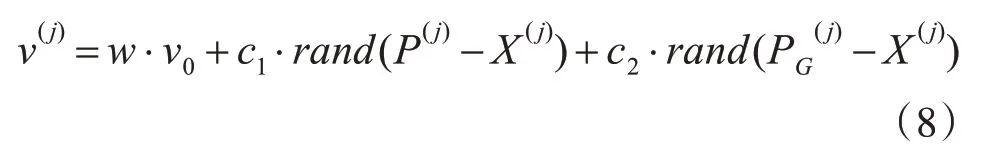
由式（8）可知，粒子更新速度主要受惯性权值w的影响。当w取值较大时，粒子的运动速度变化快，在全局寻优性能较强，但不利于后期寻找最优值；当w取值较小时，粒子运动速度变化小，无法在大范围内搜索，容易陷入局部最优值。常见调整惯性权值的办法是线性调整法，根据其迭代次数的变化而改变其值，但会存在陷入局部最优的情况。

为了平衡PSO算法的全局搜索能力及局部优化能力，本文引入非线性的动态惯性权重系数：

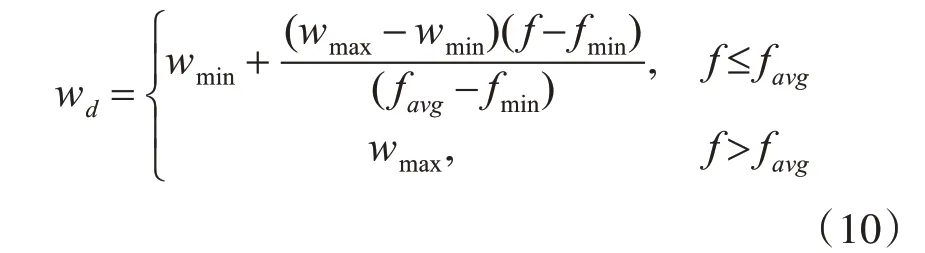
式中wmax与wmin分别代表权重的最大最小值，f为粒子适应度，favg，fmin分别为当前粒子的平均适应度和最小适应度。

式（10）中wd会随f进行调整，对于f较优的粒子，减小其w值，在其附近寻求最优值；而f趋于一致或趋于局部最优时，w增加，增加其搜索广度，使得粒子寻找全局最优解。

综合上述两种方式，得出新的惯性权重公式为

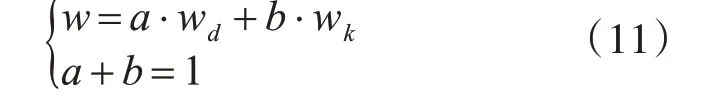
4.3 PSO算法流程

确定其适应度函数后，整个优化流程如图3所示。

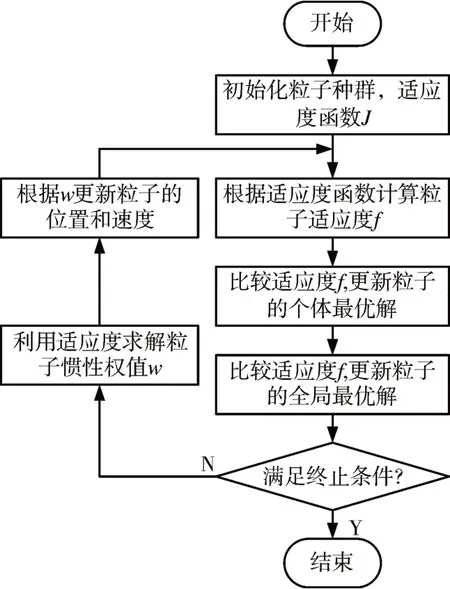
图3 PSO参数优化流程图

初始化完成之后求解粒子适应度，判定个体最优值与全局最优值，若不满足控制要求，再计算惯性权值，并更新粒子的位置与速度，反复迭代，直至寻到最优解。

5 系统仿真

根据第二节给定的稳定平台数学模型，在Matlab/Simulink中搭建方位轴的仿真模型，并设计稳定环节的ADRC控制器，实现PSO对观测器的参数优化，仿真模型如图4。

图4 光电稳定平台仿真模型

为了验证系统的稳定性能，对比PSO-ADRC与ADRC两种控制器在在给定阶跃信号下时不同的扰动及负载情况下的稳定精度，并且对比其在正弦信号下的跟踪精度。

为了保证控制系统运行稳定，将其速度值限制在1.5rad/s，其控制器参数分为ADRC与PSO两部分，确定参数部分如表1所示。

表1 ADRC与PSO部分参数

将普通ADRC控制器的三个观测系数β01、β02、β03分 别 设 置 为100，1500，5000，设 定PSO-ADRC控制器初始种群数为30，最大迭代次数为30，PSO误差阈值设置为2%，通过迭代寻求观测系数的最优值。给定1rad阶跃信号，其参数寻优历程图和优化参数控制曲线分别如图5和图7所示。由图5，可知PSO参数优化后控制器超调量为2.1%，调节时间为1.1s，优于常用的ADRC。2s时突加负载的情况下，PSO优化的ADRC抗扰动能力更强，位置波动峰值小于7mrad，并在0.3s内恢复稳态，完全可以满足稳定平台性能要求。

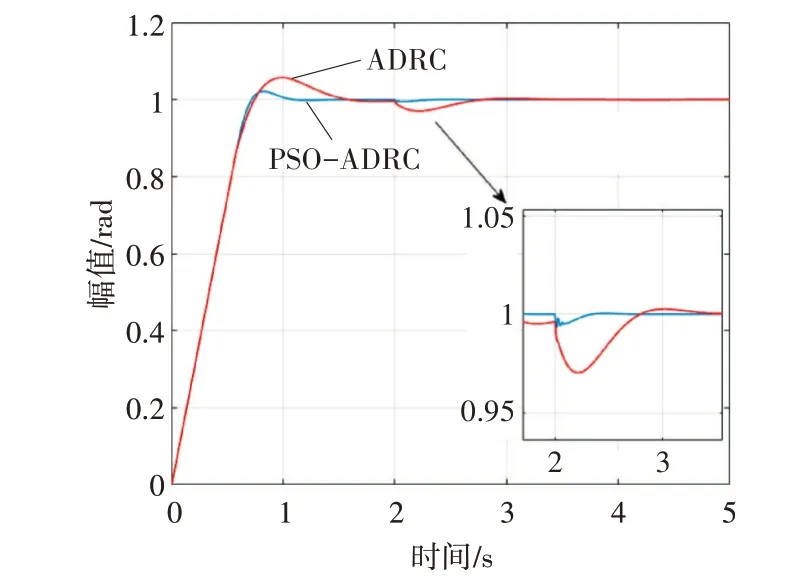
图5 角度跟踪响应曲线图

图7 最优个体适应度曲线

针对系统的抗扰能力，考虑施加系统要求的2度1Hz的正弦位置信号，等效于速度环上施加0.219sin（2*pi*t）的扰动信号，由图6可知，其引起的扰动信号可以降低至0.05mrad，也优于经典ADRC控制器。

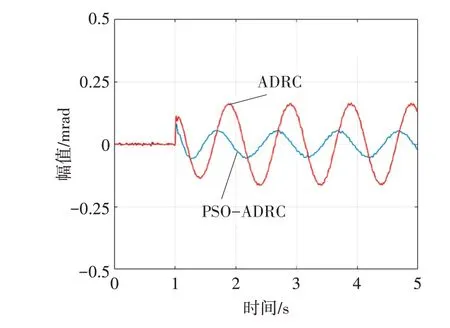
图6 正弦扰动信号响应曲线图

6 结语

本文针对无人机载的光电稳定平台，设计了速度与位置双环的稳定控制，其位置环采用PSO参数优化的ADRC控制器，通过变权重的粒子群算法优化扩张状态观测器的三个观测权值。通过对方位轴伺服控制及扰动补偿的Simulink仿真，证明了该控制器能稳定、精准地补偿载体的姿态扰动，稳定精度达到1mard以上，对光电稳定平台的算法实现具有重要的指导作用。