基于运动方程的弹道导弹建模仿真方法

赵 蒙，王明宇，王 健，乔 睿

(1.空军工程大学 防空反导学院， 西安 710051； 2. 93792部队， 河北 廊坊 065000)

1 引言

弹道导弹具有射程远、速度快、威力大、突防能力强、打击精度高等特点，已经成为现代高科技战争中的杀手锏武器。由于弹道导弹弹头RCS非常小而且还携带有强电磁干扰，一般预警雷达系统难以稳定的跟踪目标，为此，如何获取相对准确的弹道数据是众多研究者关注的热点之一[1-5]。目前主要有2种途径，一种是通过卫星、雷达等设备的实测数据来拟合、外推弹道目标的弹道轨迹；另一种是通过数据仿真的方法来生成目标弹道轨迹[6-7]。事实上，在战前几乎无法通过第一种手段获敌方弹道导弹弹道轨迹数据，为此弹道仿真技术成为分析对手弹道数据的首选方法。近些年来，国内外学者在弹道仿真方面开展了大量研究工作，但是不同程度的存在一些不足之处，文献[8-9]根据弹道目标运动规律，分别建立了弹道目标动力学方程和运动学方程用于弹道飞行轨迹的预测，但是所建模型中没有包含弹道导弹主动段模型。文献[10]根据弹道导弹性能建立了包含不同飞行阶段的弹道模型，但是该方法没有考虑弹道导弹在主动段的飞行特性。文献[11]在分析导弹各阶段受力情况的基础上，建立了参数时变的多级弹道模型，但是该模型只是在导弹速度矢量和位置矢量所决定的平面内建立二维的运动模型。文献[12]在分析常用弹道仿真模型的基础上，提出了一种基于运动学模型与历史实测数据的弹道仿真方法，但该模型无法实现全弹道的仿真，并且仿真精度还受到测量数据的影响。文献[13]以流体力学原理为基础，提出一种适用于弹道实时仿真的低空风切变复合模型，但该模型适用范围有限，只能应用近地上空弹道仿真。文献[14]依据弹道导弹不同阶段的运动特性建立了6自由度仿真模型，并利用遗传算法研究了弹道参数优化问题，但是忽略了主动段飞行程序的部分约束条件。

本文在深入分析弹道导弹主动段飞行方案的基础上，分三步设计了弹道导弹主动段运动程序，根据弹道导弹在主动段、自由飞行阶段和再入段的受力情况，联合主动段飞行程序，构建了包含了摄动力、大气阻力等因素的弹道导弹全弹道动力学和运动学模型，并对弹道导弹在各阶段的运动特性进行了仿真研究，以期为反导拦截系统研究分析弹道导弹的运动特性、规律提供一定的参考和借鉴。

2 主动段模型

2.1 主动段飞行程序设计

弹道导弹主动段飞行程序是指导弹主动段俯仰角随时间变化的规律，主动段飞行程序的设计是弹道导弹总体设计工作中的重要组成部分，直接影响导弹战术、技术指标能力的有效发挥[15-16]。设飞行过程中导弹倾角为φ(t)、弹道倾仰角为φ(t)、导弹攻角为α(t)，三者关系如下：

φ(t)=φ(t)+α(t)

(1)

在主动段由于导弹要穿越稠密大气层、克服大气阻力，为了减小空气动力对弹道的影响，弹道在整个主动段飞行过程中攻角α(t)一般都趋近于零(不大于3°)，一般可忽略不计，因此可认为弹道导弹在主动段飞行过程中其推力方向始终与速度方向一致。主动段不仅要尽快使导弹穿越稠密大气层以减小阻力带来的速度损失，还要考虑导弹转弯时的法向过载使导弹具备较高的操纵效率。为了满足这些要求，弹道导弹主动段飞行程序通常又细分为3个阶段，分别为垂直上升段、转弯段、瞄准段，最终使导弹在主动段终点达到理想的弹道倾角φe(t)和速度矢量Ve。对于单级导弹，其主动段的飞行程序通常按以下方式设计。

垂直上升段(0～t1)：垂直起飞能够让导弹快速穿越稠密大气层减小空气阻力的影响，但是时间t1不宜过大也不能太小，过大不仅容易造成弹道转弯过载增大，而且还会增加重力带来的速度损失。t1取值过小，无法保证导弹推力发动机在t1时刻达到额定工作状态。在0～t1时间内，导弹倾角、弹道倾仰角、导弹攻角分别为：

(2)

t1通常是根据导弹的重推比确定，一般来说导弹的重推比越小，导弹的推力就越大，所以主动段的加速度就越大，导弹就可以在较短时间内达到相应的高度，因此垂直上升段时间t1就可适当取小一点。反之导弹的重推比越大，t1的取值应该大一些。

转弯段(t1～t2)：在t1～t2时间段由于导弹开始按照飞行程序角进入转弯状态，导弹的攻角α(t)不等于零，为了减小空气对导弹转弯的影响，必须控制攻角α(t)的大小。在转弯段飞行程序设计时，通常要依据导弹的飞行状态控制攻角的幅度，在这个阶段导弹倾角、攻角由式(3)确定。

(3)

瞄准段(t3～tend)：为了便于弹道导弹在主动段结束时刻tend处顺利实施头体分离、减小弹头的落点散布，该段时间中导弹的倾角φ(t)设计为一常值，因此也可称为常值飞行段。该阶段内导弹的倾角基本保持不变，即

φ(t)=φ(t3)

(4)

上述内容为弹道导弹主动段飞行程序设计的一般工程实践方法，对于担负具体作战任务的弹道来讲，需要根据具体的作战需求设计满足要求的飞行程序。

2.2 导弹受力情况

在导弹的实际飞行过程中，由于实际的物理现象和过程往往非常复杂，为了便于建立模型，需要对一些过程和变量进行近似等效。建模过程中将导弹的运动视为质点运动，导弹在主动段飞行过程中，主要受到推力、地心引力、空气阻力、升力、柯式惯性力、牵连惯性力、摄动力等，下面对弹道导弹的受力情况进行分析。

在主动段，为了保持导弹的稳定性弹道导弹的攻角非常小，基本是一个重力转弯过程，而发动机推力的方向始终沿着弹体轴线方向，所以推力加速度方向与导弹的速度方向一致。设导弹的发动机推力为P，则推力加速矢量为：

(5)

空气阻力的矢量方向始终与导弹速度矢量的方向相反，空气阻力加速度可以表达为：

(6)

式中：Cd是阻力系数；S为导弹的等效横截面积；ρ为大气密度；m(t)为导弹的瞬时质量。

大气密度ρ是高度的函数，可表达为

ρ=ρ0e-kh

(7)

其中：h为导弹距离地面的高度；ρ0=1.22 kg/m3；k=0.141 41×10-2m-1。

导弹的瞬时质量m(t)与导弹起飞质量、燃料消耗率、燃烧时间有关，可表示为

(8)

地心引力加速度伴随着导弹的整个飞行过程，由于导弹与地球的距离远远小于与其他星球的距离，因此其他星球对导弹的引力相对于地球对导弹的引力非常小，可忽略不计。设导弹的位置矢量为r，则其重力加速度矢量为：

(9)

在弹道导弹运动过程中，除受到重力、推力、空气阻力之外还受到柯式惯性力、牵连惯性力、摄动力的影响。由于柯式惯性力、牵连惯性力对导弹的运动轨迹影响很小，基本可忽略，因此只考虑地球摄动力影响，有

(10)

式中：J2=1.082 63×10-3；re为地球半径；rx、ry、rz分别为r在各轴的分量。

所以弹道导弹在主动段的加速度向量可表示为：

a=ap+ag+ad+ah=

(11)

2.3 主动段模型

在地心惯性坐标系下，设弹道发射时的方位角为θ，忽略导弹的横向运动，根据弹道导弹在助推段飞行过程中的受力情况，可得助推段弹道导弹质心的运动方程为

(12)

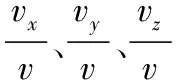
在主动段，弹道导弹的倾角主要是按照飞行程序的设计进行变化。

2.4 模型求解

(13)

其中n为迭代步长。因此给定弹道导弹目标参数及其初值，利用Runge-Kutta积分就可以得到任意时刻目标的运动状态信息。

3 自由飞行段模型

一般情况下，在弹道导弹的主动段发动机关机之后，弹道导弹进入自由飞行阶段，此时弹道导弹基本已经穿过大气层，近似在真空中飞行，大气对弹道导弹的阻力几乎为零，所以在自由飞行段弹道导弹只受到重力和摄动力的影响，因此自由飞行段弹道导弹质心的运动方程为

(14)

在自由飞行段，弹道导弹倾角主要是在重力的作用下缓慢变化，在导弹高度上升段逐渐减小，达到弹道最高点时弹道倾角为零。在导弹高度下降段导弹的倾角值为负并且不断减小。φ(t)由t时刻导弹的位置矢量r和速度矢量v决定，具体可通过式(15)计算。

(15)

4 再入段模型

在弹道导弹再次进入大气层后，弹道导弹主要受到大气阻力、地心引力和摄动力的影响，弹道导弹的弹头既有纵向的运动、又有横向的运动，当横向运动比较小并被忽略时，在弹头再入大气层运动过程中，始终认为弹头在再入大气层时的速度矢量和再入大气层时的位置所决定的平面内运动。因此再入段弹道导弹质心的运动方程为

(16)

该阶段的导弹倾角与自由飞行段的弹道倾角计算方法相同。

5 仿真验证

5.1 仿真参数

以射程3 000 km左右、两级火箭发动机的弹道导弹为例，在地心惯性坐标系下对模型的有效性进行仿真验证，设弹道导弹的发射点坐标为(-323 637，-5 144 076，3 744 779)，地理坐标为东经86.40°、北纬36.06°，弹道导弹的仿真参数见表1所示。

表1 仿真参数

5.2 主动段飞行程序

按照弹道导弹主动段飞行程序设计，主动段的飞行程序主要是导弹飞行倾角随时间的变化规律。多级火箭助推的弹道导弹其转弯段主要由一级火箭实现，主要原因是在该阶段内导弹的飞行速度相对较小，有利于实现快速转弯。根据弹道导弹的相关参数，设置主动段的垂直上升时间t1=15 s，转弯时间t2=40 s，瞄准段时间t3=10+2+50 s。其中2 s是一级火箭与二级火箭助推器级间分离时间，50 s是二级火箭燃烧时间，主动段飞行程序如图1所示。由图1可见，所设计的飞行程序在弹道导弹垂直起飞段结束后开始执行程序转弯，转弯开始时导弹的速度较小，此时弹道以较大的角速度进行转弯，实现导弹的快速转弯。到转弯后期随着导弹速度的不断增大，转弯的角速度逐渐减小，导弹进入缓慢转弯状态，达到了转弯过程中保持导弹运动稳定性的要求。

图1 主动段飞行程序曲线Fig.1 Flight program curve of the active phase

5.3 仿真结果

根据弹道导弹在各阶段的运动方程，使用四阶Runge-Kutta积分解算弹道方程，根据计算得到弹道导弹的落点坐标为(-867 878，-2 935 684，5 587 847)，地理坐标为东经73.53°、北纬61.41°，射程为2 954 km，总飞行时间为1 222 s，弹道最大高度为1 058 km，到达弹道最高点的时间为648 s。

图2为弹道导弹主体弹道各个飞行阶段导弹的飞行轨迹。根据图2可见，弹道导弹的主动段和再入段在整个弹道导弹飞行过程中占比很小，大部分时间弹道导弹都处于自由飞行段，在1 222 s的飞行过程中主动段飞行时间只有117 s，基本只占整个弹道的1/10。图3是导弹弹头和两级助推器在地心惯性坐标系下的运动轨迹，一级助推器相对于二级助推器飞行过程很短，这主要是因为一级助推器分离时速度和高度相对较小。图4是弹头和两级助推器飞行高度随时间的变化曲线，由图4可见，在主动段导弹的高度随时间变化比较缓慢，并且能够清楚的获得弹道最高点高度和到达弹道最高点的飞行时间。

图2 主体弹道飞行轨迹Fig.2 Main body trajectory

图3 弹头和助推器的飞行轨迹Fig.3 Trajectory of warheads and boosters

图4 弹头和助推器飞行高度曲线Fig.4 Variation curve of flight altitude with time

图5是速度曲线，主要反映了弹头、一级和二级助推器速度的变化情况，根据弹头速度的变化情况可明显看出主动段结束时刻以及弹道导弹进入大气层的再入时刻。在主动段结束时刻弹头的运动速度达到4 750 m/s，随后逐渐减小至弹道最高点，过了弹道最高点之后又逐渐增大，直至进入大气层的再入时刻，在进入大气层后，由于受到大气阻力的作用速度迅速减小直至落地。通过导弹运动速度变化规律，能够清楚地判断出弹头和助推器的运动阶段。

图5 弹头和助推器飞行速度曲线Fig.5 Variation curve of flight speed with time

图5中蓝色的曲线是二级助推器飞行轨迹，如果不考虑器弹道系数和大气阻力对其影响，二级助推器应该和弹头飞行速度相同，但实际上二级火箭与弹头分离之前两者之间有一定的相对速度差，另外由于助推器的横截面积大于弹头的等效横截面积，相对于弹头而言助推器受到的大气阻力更大，所以在两者分离之后且未到达弹道最高点时刻，二级助推器速度减速比弹头的要明显，这也就是图中两者产生较大差异的原因。

图6是两级助推器的推力加速度曲线，一级发动机点火后其推力加速度大约为2g，随着弹道燃料的消耗，一级助推器关机时刻推力加速度达到6g左右。二级发动机点火后其推力加速度大约为4g，到主动段结束时刻推力加速达到13.5g。

图6 助推器推力加速度曲线Fig.6 Thrust acceleration curve of booster with time

图7是弹道导弹飞行全程导弹倾角(与投影点处平面的夹角)曲线，导弹在主动段结束后的自由飞行段弹道倾角逐渐缓慢的减小，在达到弹道最高点的时刻导弹倾角为0°，而后继续减小，到达再入点后，由于受到大气阻力的影响增大，弹道倾角变化速度加剧，落地时刻弹道倾角达到72°左右，所以通过弹道倾角的变化规律也能够快速判断弹道的运动阶段。

图7 导弹倾角曲线Fig.7 Missile inclination curve with time

弹道导弹弹头的跟踪识别是弹道导弹防御体系的核心环节，提前研究弹道导弹的飞行轨迹和运动规律、特点，将更有利于开展弹道导弹弹头的跟踪和识别。通过仿真得到了弹道导弹的一些运动规律以及弹道的关键参数，这些仿真得到的弹道数据基本能够全面反映弹道导弹的运动特点和运动规律，相关的结论可供弹道导弹弹道设计、目标识别的技术人员参考和借鉴。

6 结论

导弹弹道仿真技术是开展弹道导弹防御系统模拟对抗的关键技术之一，在有效获取敌方弹道目标运动轨迹数据之前，迫切需要通过模拟仿真手段来检验弹道防御系统的反导拦截效能。本文针对部分文献的不足，在设计弹道导弹主动段飞行程序的基础上，根据弹道导弹在不同运动阶段的受力情况，充分考虑大气阻力、摄动力等因素，构建了弹道导弹运动模型，通过仿真计算得到了弹道导弹的弹道高点、射程、最大速度、飞行时间、落点位置等关键弹道参数，分析了整个飞行过程中弹道导弹飞行高度、速度、倾角、加速度等随时间的变化规律，仿真结果能够全面地反映弹道导弹助推器、弹头在几个不同运动阶段的运动特性。仿真结果和结论可以为弹道导弹防御系统研究分析弹道导弹的运动特性、规律提供参考和借鉴。