电磁轨道炮试验装置动态特性动力学分析

李四超,刘可可

(1.海军装备部驻郑州某军事代表室， 郑州 450015； 2.中国船舶集团有限公司第七一三研究所， 郑州 450015)

1 引言

近年来，由于高新技术的普遍应用，许多鲜为人知的新概念火炮随之诞生。其中，美国海军主导的舰载电磁轨道炮得到了全世界的瞩目，电磁轨道炮是采用电磁推力替代火药为弹丸提供发射动力，具有初速高、射程远等高性能的新概念武器。2010年12月美国海军在弗吉尼亚州成功试射电磁炮，射程为海军常规武器的10倍，破坏力惊人，但电磁身管的质量也是传动舰炮的数倍，据报，美军海上系统司令部正在为电磁炮开发一种新型“集成炮架”，炮架的总质量将超过130 t，其中电磁身管自身质量约为18 t[1-2]。电磁轨道炮大质量身管这一特性对全炮的频率和炮口振动周期影响极大，本研究针对电磁轨道炮试验装置的发射系统进行模态分析和动力学仿真分析，探索发射过程中含阻尼机械系统所引起的振幅与衰减周期等参量的变化规律，为降低炮口振动周期与改善结构动力学特性提供技术途径。

2 模态分析

2.1 模态分析理论基础

任何零部件都有自己的固有频率，为避免结构上可能引发的不良振动，在初始设计时使这些部件的固有频率避开外部激励的频率，从而有效地减小系统振动幅值。模态分析就是求模型的固有特性，包括频率与振型等。它是以振动理论为基础、以模态参数为目标函数的分析方法，其目的就是分析和了解结构系统的动态特性，优化改进结构的动态性能。

通常N维多自由度有阻尼系统在物理坐标系下的运动方程如式(1)所示:

(1)

通过坐标变化可转化为模态坐标系下的运动方程为：

(k-ω2M+jωC)X(ω)=F(ω)

(2)

任意l点的响应是各阶模态响应的线性组合：

(3)

(4)

解耦之后的运动方程为：

(Kdia-ω2Mdia+jωCdia)Q=Fφ

(5)

其中C=αM+βK,Fφ=φTF(ω),Q={q1(ω),q2(ω), …,qr(ω)}T。

通过上述坐标转化和解耦便能计算求得系统的各阶模态。

模态有效质量或有效因子是指在某一向量激励作用下，某一模态参与的系统质量。在某一向量激励下，所有振型平动方向的有效质量之和等于各个质点的质量之和，转动方向的有效质量之和等于各个质点的转动惯量之和。有效质量的作用大致有二：其一，可以找到有效质量的最大模态，从而认真对待；其二，有助于判断所分析的模态阶数是否已经足够[3-5]。

同时在所有的振动系统中都存在着阻尼，阻尼的主要作用是转移系统的能量。合理的阻尼参数对于获取精确的结果有着重要作用。真实系统阻尼的大小由系统固有属性决定，在动力学仿真分析中，通过加入等效阻尼，将复杂的阻尼机理根据阻尼力耗散的能力用等效阻尼来替代，提高系统阻尼能有效提高振幅衰减速度。

本文针对电磁轨道炮某试验装置的发射系统进行动力学分析，使用三维软件建立有限元模型，为便于仿真计算对部件做了简化处理。试验装置有试验台架、反后坐装置、颈筒、身管组件、炮尾馈电等组成，具体如图1所示。

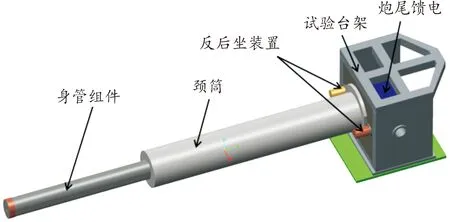
图1 电磁轨道炮某试验装置示意图Fig.1 Schematic diagram of an electromagnetic railgun test device

2.2 模态仿真分析

模态分析就是求模型的固有特性，包括频率和振型等。用商业有限元软件对试验装置进行网格划分，共产生351 945个节点，191 752个单元。为了与试验状态保持一致，在试验台架最底面施加了固定约束，经过多次迭代仿真计算，提取了对结构有较大影响的X、Y、Z、ROX、ROY、ROZ六个自由度方向的主振型与固有频率，具体主振型云图如图2—图5所示。

图2 一阶振型云图(6.791 8 Hz)Fig.2 The first order modal (6.798 1 Hz)

图3 二阶振型云图(7.136 1 Hz)Fig.3 The second order modal (7.136 1 Hz)

图4 五阶振型云图(46.155 Hz)Fig.4 The fifth order modal (46.155 Hz)

图5 七阶振型云图(61.719 Hz)Fig.5 The seventh order modal (61.719 Hz)

仿真结果如表1所示，该试验装置模态频率范围在6.7918～61.719 Hz，有效参与质量均大于85%，主要振型以弯曲为主。主要振型及其频率：X向及ROZ向旋转振型主要表现在第2阶，频率为7.1361 Hz；Y向振型主要表现在第5阶，频率为46.155 Hz；Z向及ROX向旋转振型主要表现在第1阶，频率为6.791 8 Hz；ROY向旋转振型主要表现在第7阶，频率为61.719 Hz。

下面基于多体动力学软件分析颈筒、身管和质心位置等的变化对整体振动时间、周期和幅值的影响情况。

表1 试验装置自身模态主振型

3 动力学分析

3.1 动力学理论基础

动力学主要是用于确定承受任意的随时间变化载荷结构的动力学响应的一种方法。可用来分析结构在稳态载荷、瞬态载荷和简谐载荷的随意组合作用下随时间改变的载荷所带来的动力学响应。与静态分析不同，它主要考虑随时间变化的载荷、阻尼及其惯性的影响。如果惯性力和阻尼作用不重要，就可以用静力学分析代替瞬态动力学分析。发射动力学运动方程式(1)中所示，其中F(t)代表变载荷向量。

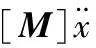
3.2 动力学仿真分析

动力学是以经典力学为基础，研究多体系统的运动与动力规律的学科，它的研究对象为体和体之间的连接，体包括刚性体和柔性体[7-10]。本文采用通用多体动力学软件对试验装置进行刚柔耦合仿真，其中颈筒和试验台架设置为柔性体，炮尾馈电等设置为刚性体，然后改变试验台架的板厚、试验台架和颈筒施加的阻尼、身管组件的质量、炮质心的位置和改变施加后坐力时间进行仿真，通过对比分析得到一些趋势性结论，为后期结构优化方向提供理论参考。其仿真结果如下：

1) 试验台架板厚变化(3 mm、5 mm、10 mm、20 mm)

从图6中得到，同种板料，随着厚度的增加，即增强台架的强度和刚度，总衰减时间减小，振动周期减小，振动幅值减小。

2) 试验台架阻尼系数变化(0、0.2、0.5、1)

从图7中看出，随着试验台架阻尼系数的增大，总衰减时间减小，振动周期基本不变，振动幅值基本不变。

3) 径筒阻尼系数变化(0、0.3、0.5、1)从图8中明显地看出，随着径筒阻尼系数的增大，总衰减时间减小，振动周期基本不变，振动幅值基本不变。

4) 身管组件的质量变化(12 t、16 t、24 t、28 t)

从图9中看到，随着身管组件质量的增加，会引起不平衡力矩增大，则造成总衰减时间增大，振动周期增大，振动幅值变化不大。

5) 炮质心相对于初始位置的距离(0 mm、1 500 mm、2 000 mm、2 500 mm、3 000 mm、3 500 mm)

从图10中看到，随着身管质心相对于初始位置逐步前移，即转动惯量越来越大，造成总衰减时间增大，振动周期增大，振动幅值增大。

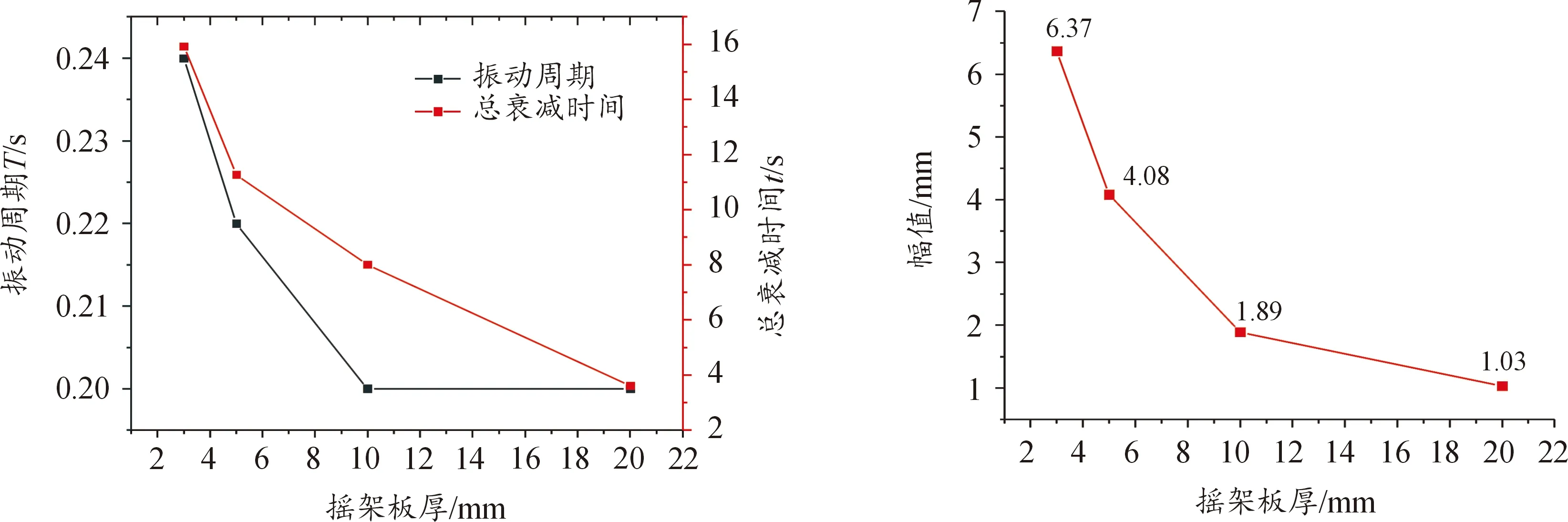
图6 台架厚度的变化对振动情况的影响曲线Fig.6 Influence of bench thickness variation on vibration conditions

图7 试验台架阻尼系数变化对振动情况的影响曲线Fig.7 Influence of damping coefficient variation on the vibration of the test bench

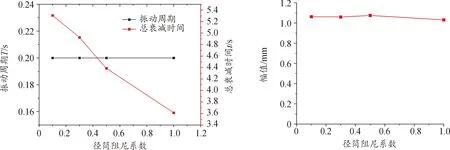
图8 颈筒阻尼系数变化对振动情况的影响曲线Fig.8 The influence of damping coefficient variation on vibration of the tube

图9 身管质量变化对振动情况的影响曲线Fig.9 Influence of weight change on vibration

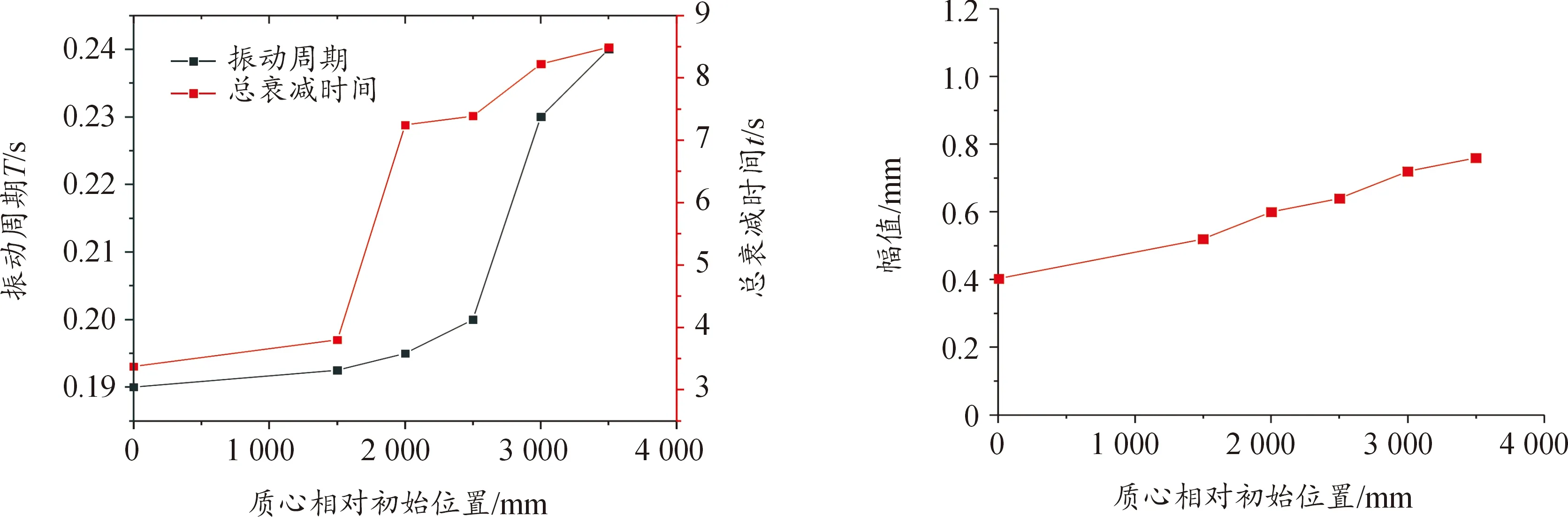
图10 炮质心位置变化对振动情况的影响曲线Fig.10 Influence of gun centroid position change on vibration

4 结论

模态分析和动力学仿真结果表明，大质量负载(比如长悬臂身管)降低了系统的频率，特别是低阶频率；身管组件质量越大，惯性力越大，频率越低，刚度越低，振动周期越长。因此，降低身管组件质量与炮管重心后移都能有效提高固有频率，降低系统的单个振动周期。研究结果显示试验台架阻尼系数和径筒阻尼系数对振动周期影响很小，可以为发射平台的机械结构优化、弹炮性能匹配和试验评估提供依据。