基于PD控制算法与Isight系数优化的无人机轨迹跟踪
2023-01-06柳文林潘子双崔凯凯
柳文林,潘子双,崔凯凯
(1.海军航空大学 航空基础学院, 山东 烟台 264001; 2. 92942部队, 北京 100161)
1 引言
近年来,随着计算机软硬件以及信息化技术的快速发展,无人机(unmanned aerial vehicle,UAV)在遍及情报侦察[1]、目标跟踪[2]、电力巡检[3]、应急救援[4]和货物配送[5]等诸多军事和民用领域发挥着愈来愈重要的作用。轨迹跟踪控制是无人机发挥任务执行能力的底层技术实现,在国内外研究人员中引起了广泛的关注[6]。
就无人机轨迹跟踪控制问题而言,其核心是控制律的设计,当前国内外提出的方法主要有比例-积分-微分(PID)控制、反步法(Backstepping)和H∞控制等。PID控制是一种发展较早的经典控制方法,在各类实际的工程控制系统中应用广泛[7-9],文献[10]中针对微小型无人机设计了带死区变增益PID控制律。反步法以Lyapunov稳定性原理为基础,将系统分解为多个子系统,采用由前至后进行递推的设计实现系统稳定[11],相较而言该控制方法求解过程较为复杂,需要调节的控制参数也较多。文献[12]中在李雅普诺夫方法的基础上进一步设计了抗干扰的反步控制算法。近年来,鲁棒控制理论逐渐兴起,最为典型的是H∞控制理论,其通过设计反馈控制器,使闭环系统稳定且闭环传递函数阵的H∞范数最小或小于某一给定值,从而使被控对象满足性能要求。文献[13]中为适应无人机平台低性能飞控计算机的计算能力,对鲁棒H∞控制器进行了降阶和离散化处理,并通过了半物理仿真实验的验证。除此以外,滑模变结构控制[14]和动态逆控制[15]也被广泛应用于无人机轨迹跟踪控制,但前者存在保守性大和控制量易饱和的问题,后者受飞行器建模精度的影响较大,在实际工程应用中需要考虑抗扰动的问题。
在控制参数优化方面,由于控制参数较多、求解空间较大且呈现非线性特征,所以往往采取智能优化算法进行寻优。常见算法有遗传算法[16]、粒子群算法[17]以及蜂群算法[18]等。
本文中针对无人机轨迹跟踪问题,选用较为常见的PD控制算法,控制模型简洁高效;基于Isight软件,将多岛遗传算法和序列二次规划算法结合加快寻优速度并提高解的质量,最终实现无人机对参考轨迹的良好跟踪效果。
2 无人机动力学模型建立
考虑到现实情况的复杂性,建立精确的无人机动力学模型十分困难,为便于研究,本文中做出如下假设:
1) 不考虑无人机的弹性形变及质量变化;
2) 忽略地球曲率及自转的影响;
3) 不考虑重力加速度随高度的变化。
参考文献[19],可推导出三维空间中固定翼无人机质心动力学方程组在航迹坐标系中的形式为:
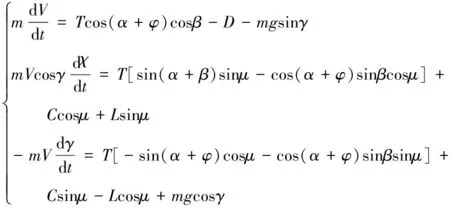
(1)
无人机的运动学方程为:
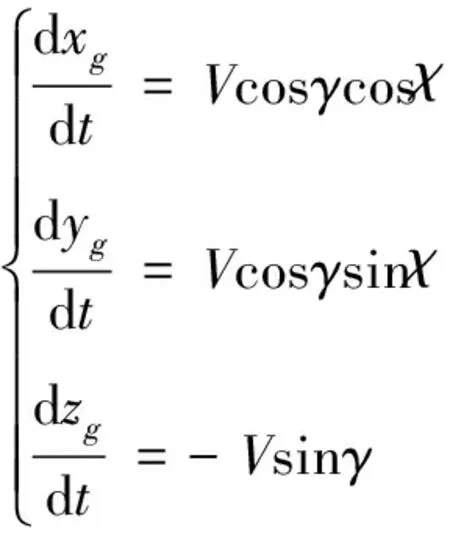
(2)
其中:m为无人机质量;(xg,yg,zg)为无人机在空间中的位置坐标;V为飞行速度;T为发动机推力;D为气动阻力;C为气动侧力;L为气动升力;χ,γ,μ分别为航向角、航迹倾角和速度滚转角;α,β分别为迎角和侧滑角;φ为发动机安装角。
为进一步简化模型,设无人机处于小迎角、无侧滑飞行状态,且发动机的推力沿着飞行速度方向。即假设φ=0,α≈0,β≈0,通常无人机所受侧力C主要由侧滑角导致,因此,C≈0。于是可将方程式(1)简化为以下形式:
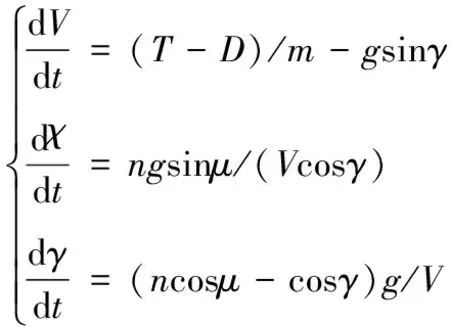
(3)
通过上述简化过程,可由式(2)和式(3)得到状态变量X=[xg,yg,zg,V,χ,γ]T和控制变量U=[T,μ,n]T之间的非线性关系式。这里为实现线性化控制,引入新的控制变量[20]:
(4)
设ξ=[xg,yg,zg]T,则有:
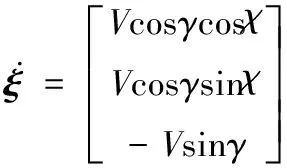
(5)
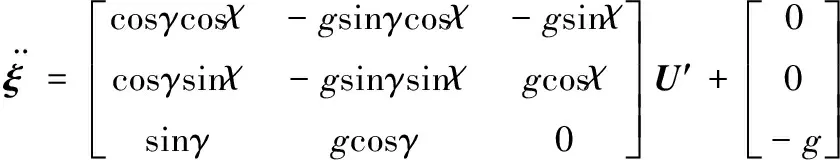
(6)
其中,
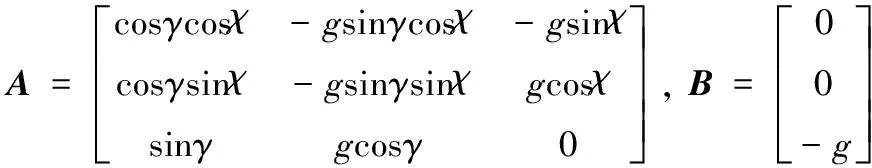
(7)
如此,即可实现非线性控制方程的线性化。又因为det(A)=-g≠0,所以可以进一步通过设计虚拟变量h的控制律,并按照式(8)求得真实的控制变量U′
U′=A-1(h-B)
(8)
又,无人机的气动阻力通常可以表示为:
D=qSCD0+CA(nmg)2/(qS)
(9)
所以,原始控制变量U的表达式可写为:
(10)
3 控制算法设计
本文中采用最为常见的PD控制算法对无人机进行轨迹进行跟踪控制,并基于Isight软件,采用多岛遗传算法(Multi-Island Genetic Algorithm)和序列二次规划法(NLPQL)相结合的方式进行控制系数的优化。
3.1 PD控制算法
采用PD控制算法的控制律为:
(11)
这里的Kp和Kd分别为比例系数和微分系数矩阵,为了方便处理,将2个矩阵均选为对称阵:
(12)
在PD控制算法中,系数的选取直接影响到控制的效果,下面采用Isight软件对控制系数进行优化。
3.2 控制系数优化
轨迹跟踪控制的目的是使无人机的实际飞行轨迹尽量贴合预期规划轨迹,因此选取总路径偏差作为优化目标。又出于延长无人机作战周期的目的,额外考虑整个控制过程中的推力总和用以表征能量消耗。综上,构建整体优化模型为:
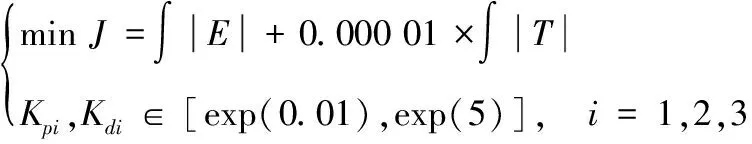
(13)
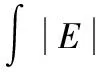
Isight软件由美国Engineous公司开发出品,有机融合了试验设计、近似建模、探索优化和质量设计四大数学算法并具备广泛的CAD/CAE以及自编程序集成接口,用户通过拖拽的方式就可以快速搭建并管理复杂的仿真流程,运用多种优化算法得到最终的优化方案,从而大大缩短产品研制周期,降低研发成本[21]。因此,Isight软件广泛应用于汽车[22]、航空[23]、航天、船舶、兵器[24]等多个领域。本文在优化算法的选取上,也利用Isight软件中的Task Plan组件集成全局优化算法和数值优化算法进行优化设计。首先应用全局优化算法快速定位目标极值在设计空间中所处的区域,再应用数值优化算法对该区域进行精确寻优,最终获得最佳设计结果。该策略的优点在于[21]:
1) 发挥了全局优化算法在整体设计空间遍历方面的优势,能够快速对设计敏感区域进行定位;
2) 仅应用全局优化算法对设计空间进行粗略定位,避免了全局算法在细节优化方面的效率问题;
3) 发挥了数值优化算法在局部优化方面的优势,能够精确的找到设计最优解;
4) 避免了数值优化算法在高度非线性或离散设计空间中直接寻优可能给用户带来的误导。
就具体优化算法的选择而言,首先,利用多岛遗传算法(Multi-Island Genetic Algorithm)在指数坐标下对控制参数进行优化,获得最优解。之后再利用序列二次规划法(NLPQL)对多岛遗传算法求解得到的最优值附近区域内进行搜索,进一步提高优化效果。具体的优化流程如图1所示。
其中,Optimization1选用的优化算法为多岛遗传算法,其作为一种分布式改进型遗传算法,具备较强的全局求解能力,可以提高整个优化过程的计算效率;Optimization2选用的优化算法为序列二次规划算法,其作为一种梯度优化算法,可以在局部范围内快速探索,进一步完善解的最优性。
4 优化过程仿真及结果分析
基于前文设计的PD控制算法以及搭建的Isight控制系数优化工作流,对无人机轨迹跟踪控制展开仿真分析。
4.1 仿真参数设置
在仿真过程中,无人机的参数设置采用文献[25]中“RQ- 4A全球鹰”无人机的有关数据以及文献[26]中的算例,其主要性能参数如表 1所示,单位均为国际标准单位。

表1 无人机性能参数
设置参考轨迹为空间正弦曲线:
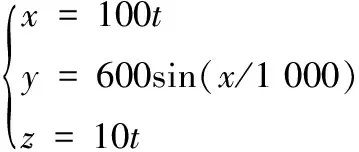
(14)
无人机初始位置为x(1)=10,y(1)=-50,z(1)=20,初始速度为Vx(1)=10,Vy(1)=80,Vz(1)=20。大气条件使用MATLAB软件中的国际标准大气模型。
Isight软件中优化器Optimization1和Optimization2的算法参数设置如表2所示。

表2 算法参数
4.2 结果分析
将整个优化流程框架重复运行20次,取最优结果。优化过程如图2所示,其中左图多岛遗传算法共运行1 001步,右图序列二次规划算法共运行459步,最终得到优化结果如表 3所示。
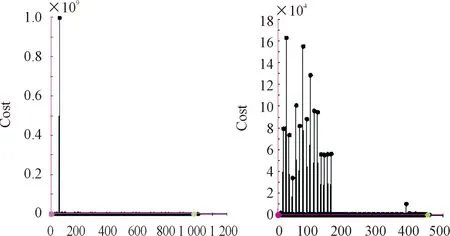
图2 优化过程示意图Fig.2 Optimization process
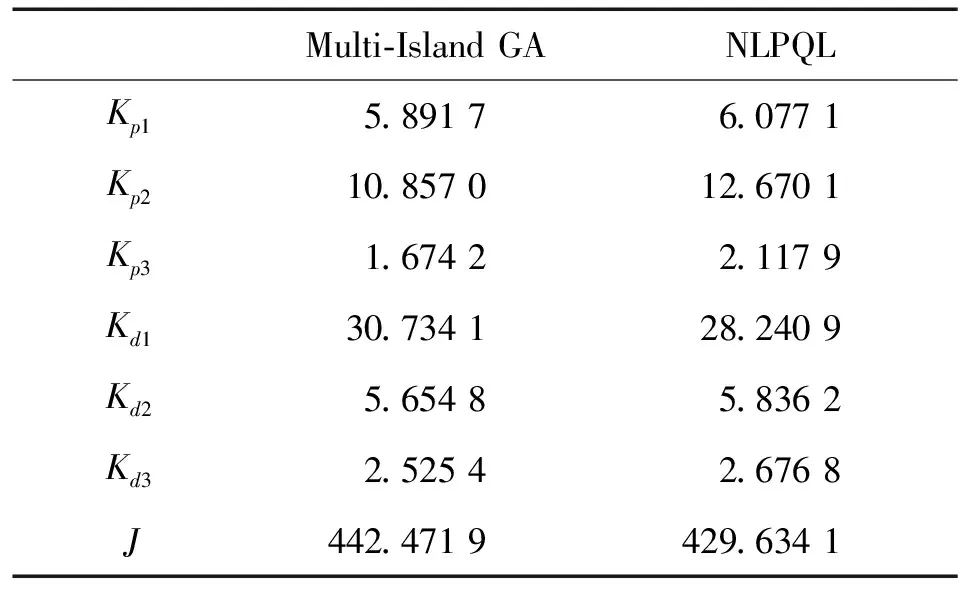
表3 组合优化结果Table 3 Combinatorial optimization results
由表3可以看出序列二次优化算法能够在多岛遗传算法的结果附近进行二次寻优,主要是进一步优化了Kp1的取值,并将目标函数的数值由原来的442.57减小到429.63,使得目标函数减小2.9%,可见,文中所采用的组合优化算法达到了进一步提高参数优化效果的预期。获得相应的控制矩阵最终优化结果为:
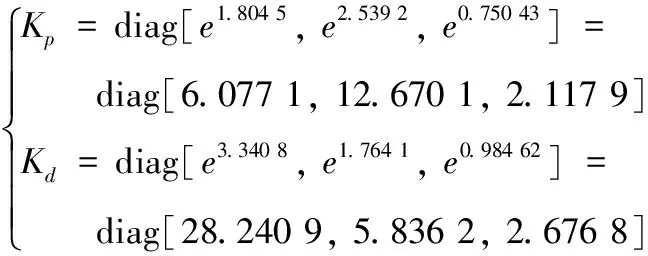
(15)
利用优化所得的控制系数对无人机轨迹进行控制,最终获得的轨迹曲线如图3。可以看出该控制算法除了在起步阶段以及转角处存在一定的偏离,整体上可以较好地实现对参考轨迹线的跟踪。
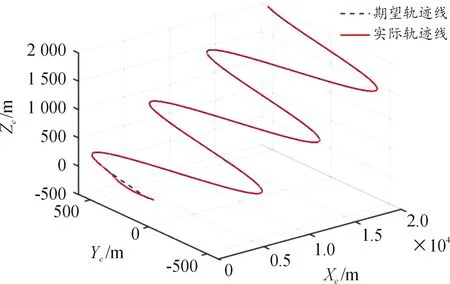
图3 无人机轨迹跟踪效果曲线Fig.3 UAV trajectory tracking performance
进一步研究无人机路径跟踪过程中,各个参数的变化情况,由图4所示位置和速度标量误差曲线可以看出,飞行过程中,无人机路径跟踪的位置稳态误差和速度稳态误差的最大值均基本为0。因此,本文中设计的算法可以实现对参考轨迹较好的跟踪。此外,无人机轨迹跟踪过程中的推力变化曲线、速度滚转角变化曲线以及过载变化曲线如图5—图7。
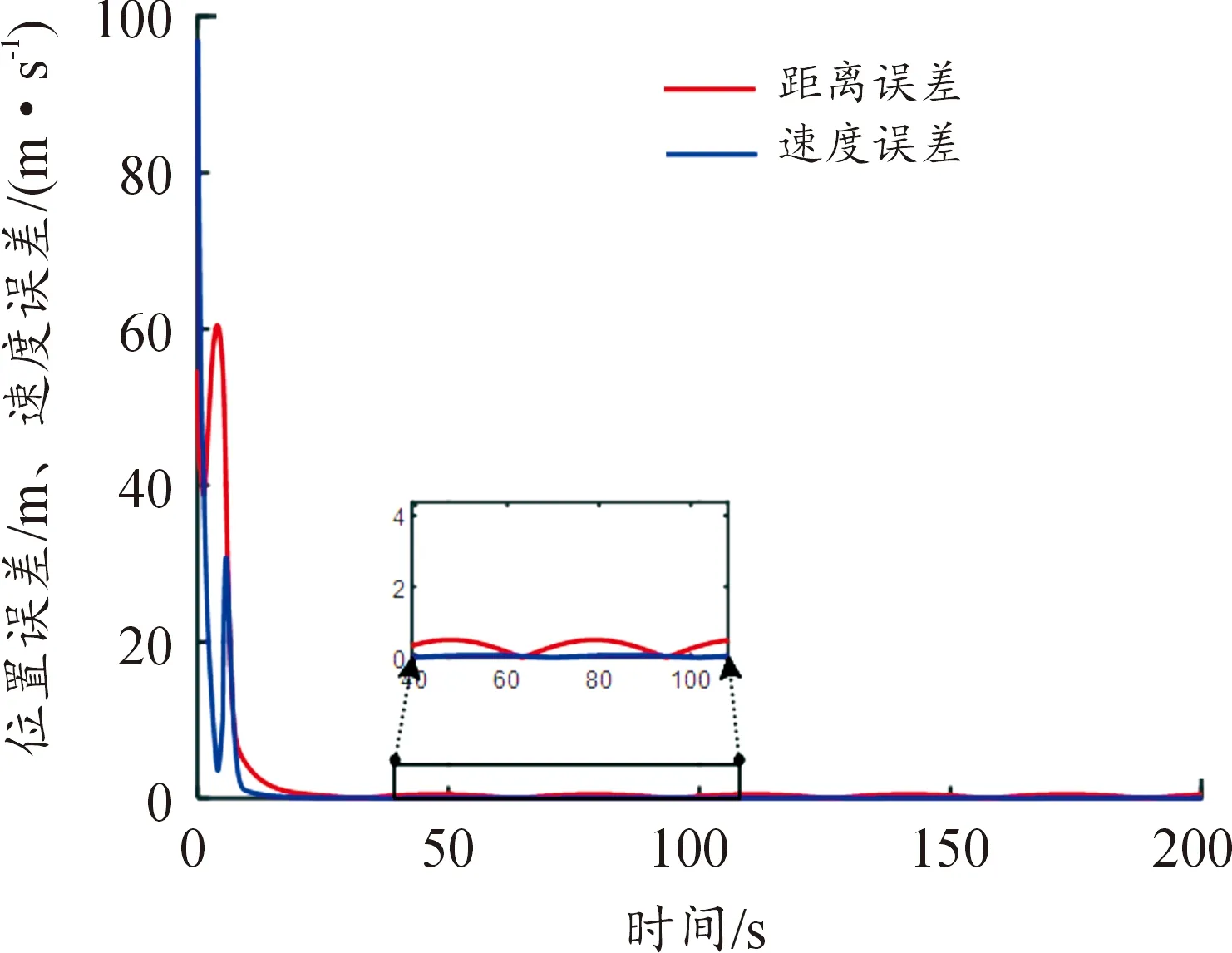
图4 位置、速度标量误差曲线Fig.4 Position and velocity scalar error

图5 推力变化曲线Fig.5 Thrust variation curve
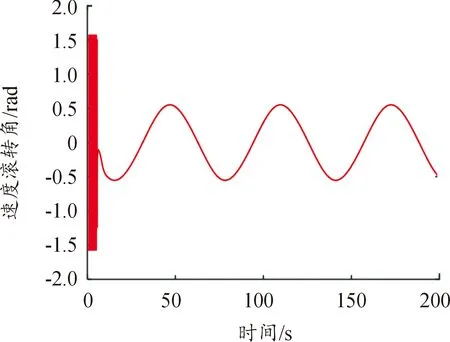
图6 速度滚转角变化曲线Fig.6 Speed roll angle variation curve
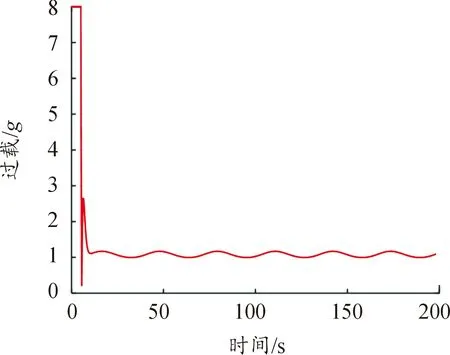
图7 过载变化曲线Fig.7 Overload variation curve
综上,采用本文中设计的PD控制算法可以较好地实现无人机对参考轨迹的跟踪控制,飞行过程中产生的位置误差与速度误差均能控制在可接受的范围内;基于Isight软件搭建的控制参数优化流程可以实现控制系数的优化,从而达到良好的控制效果。
5 结论
基于已有的研究建立了无人机飞行的动力学模型,根据所建立的动力学模型设计了PD控制算法来对无人机进行轨迹跟踪控制。并利用组合优化算法的思想,采用Isight软件对PD控制系数进行优化。仿真结果表明,在路径跟踪过程中,无人机的位置误差最大值趋于0,可以较好地实现无人机路径跟踪的功能;基于Isight软件搭建的控制参数优化流程框架可以控制系数的优化,提高控制效果,特别是采用多岛遗传算法的并行计算机制,加快求解速度,进而采用串行结构与序列二次规划算法结合,将代价函数减小了2.9%,提高了解的最优性。
