教与学算法在复杂边坡临界滑动面搜索中的应用

吴剑平 汪东林

(安徽建筑大学 土木工程学院,合肥 230601)

边坡稳定性问题涉及到基坑工程、矿业工程、水利工程和公路工程等岩土工程领域的各个方面,然而稳定性评价函数受土壤参数、地面条件等复杂边坡环境的影响,常常峰值众多,致使传统的优化算法(变分法[1]、模式搜索法[2]、动态规划法[3]等)无法有效应对,容易陷入局部收敛,因此迫切需要寻找和开发出可靠的解决方案.自20世纪70年代以来,计算机技术快速发展,智能优化算法在边坡滑裂面搜索中的应用逐渐成为研究的热点,如:遗传算法[4-6]、蚁群算法[7-8]、狼群算法[9]和蜂群算法[10]等.但是,它们大多都有结构复杂、参数众多且参数值难以确定的缺点,不利于实际工程的应用.

教与学算法(teaching-learning-based optimisation algorithm,TLBO)是由Rao等[11]于2011年首次提出的,是一种启发式群体智能优化算法,具有容易理解、易于编程、无需微调参数、收敛速度快和全局优化性能强的优点,且目前在电网系统的无功优化领域有着较为成熟的应用[12-13].本文将TLBO 应用于边坡圆弧滑动面的搜索中,并结合简化Bishop法,编写Matlab程序,通过对土坡算例计算结果的统计和对比分析,验证了该算法在边坡滑动面搜索中的可行性.

1 边坡滑动面搜索的优化模型

1.1 简化Bishop法

在边坡稳定性计算方法中,简化Bishop法凭借其简单、精确的优点[14],一直备受科学研究和工程实践的青睐.简化Bishop法忽略了条间剪力的作用,不考虑水平方向力的平衡,并基于强度折减原理和Mohr-Coulomb准则,推导出安全系数计算公式如下:

式中:ci为黏聚力;φi为内摩擦角;Wi为条块重力;bi和αi分别为条块宽度和条底倾角.

1.2 变量设计和目标函数的建立

传统上,圆弧滑动面的搜索问题以圆心坐标(xo,yo)和半径r作为设计变量[4,6],但是这样会造成许多问题:其一,变量xo、yo和r的范围难以确定;其二,要考虑在搜索范围内随机产生的圆弧是否与坡体相交;其三,当边坡坡面复杂无规则时,滑面与坡面交点的确定将会变得极为复杂.为避免这些问题,本文选择滑面与坡面左右两个交点的横坐标xs和xe以及圆心的纵坐标yo作为设计变量.

变量确定后,根据坡面方程surf(x)和圆的几何性质,很容易求得纵坐标ys、ye和圆心横坐标xo:

已知圆心坐标(xo,yo)与圆弧任意一点的距离r(见式(5)),便可得到滑动面方程式(6):

式中:与文献[15]中yo≥0的约束不同,此方程式本身就具有保持圆弧为凹型的特征:y(x)≤yo.

滑动面方程确定后,式(1)中的几何参数和物理力学参数便可确定,进而目标函数得以建立:

式中:Ω为圆弧滑动面的可行域.

1.3 重新定义“破弧”及其解决方法

基于文献[4]对于“破弧”的描述,本文对其进行重新定义:在二维平面坐标系中,任一滑动面方程与坡面方程应有且只有两个交点,且不得穿过硬土层,除此之外皆称之为“破弧”.文献[6]基于“罚函数”的思想,对出现“破弧”问题的滑动面赋予极大的安全系数,以便借助遗传算法适者生存的仿生原理,达到排除“破弧”的目的.然而,TLBO 算法并没有类似于剔除劣等个体的功能,因此不可采用.

依据前述变量的设计,结合文献[4]给出的排除“破弧”的思路,本文通过Matlab软件编写了应对“破弧”的解决方法,其程序pohu(X)的伪代码如下:

步骤1:输入变量矩阵X.

步骤2:根据式(3)～(5)计算滑面方程(6).

步骤3:设置xs～xe范围内的取值精度为0.001.

步骤4:从横坐标xs+0.001 开始,依次计算xs～xe范围内坡面方程、滑面方程和硬土层面方程的纵坐标,并分别存储在行向量y1、y2、y3中.

步骤5:如果min(y1-y2)＞0且min(y2-y3)＞0,则未发生“破弧”,输出结果X;反之,转步骤1,再次运行程序.

1.4 优化模型

综上所述,建立边坡临界滑动面搜索的优化模型:

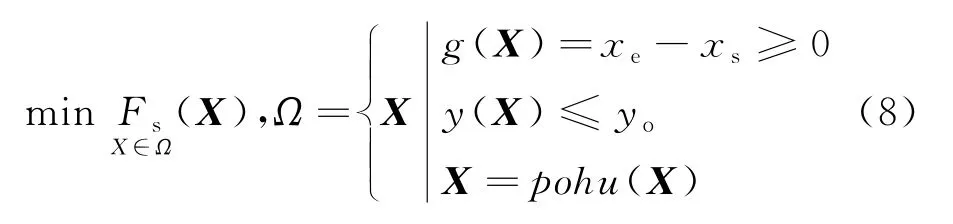
2 基于教与学算法的边坡滑动面搜索

教与学优化算法将所有的决策变量赋予学生各科成绩的意义,并借助“教”与“学”两阶段的学习方式,模拟以班级为单位的学习过程.在“教”阶段,选取班级中成绩最好的学生作为老师来指导其他学生的学习,从而实现班级整体成绩水平的提升;在“学”阶段,学生之间相互学习,以促进知识的吸收,完成共同进步.算法关键步骤如下:

1)初始化学生群体

假设班级中有n个学员,每个学员要学习3门功课:s、e和o,3门功课的成绩分别用xs、xe和yo表示,则第k次学习后,打印学生i的成绩单Xki为:

令式(9)中k=0,则即为学员还未学习时的成绩,此时每位学员各科成绩按下式计算:

综上所述,学生群体初始化矩阵X0为:

2)计算适应度值

适应度值是综合评价学生成绩优劣的标准,它贯穿算法运行的始终.本文采用目标函数Fs作为个体适应度的计算方法,且将班级中所有学生第k次学习后的适应度值存储在矩阵fk中:

3)“教”阶段

选取Fs=min(fk)的学生作为第k+1次学习时班级所有学生的老师,并将其表示为;然后,老师依据班级各科的平均成绩Xmean,依次对班级的每个学生进行教学,公式表达如下所示:

式中:TF为老师面对第i位学员时,体现其教学能力的教学因子,TF=round(1+rand),round为四舍五入型取整函数.

4)“学”阶段

“教”阶段完成后,为进一步提高学生成绩,从第一位学生开始,依次随机选择一位同学进行学习操作:

式中:i≠j,i,j∈[1,n].

5)更新成绩

为保证“教”与“学”后,每个学员的综合成绩水平有所提高,仅对正向吸收教学成果的同学进行成绩更新,即根据教学前后适应度值的大小,完成如下操作:

6)迭代终止判断

在教与学算法中,每一次计算结果都是非负向的,即不会出现学生综合成绩倒退的现象,所以随着班级成绩多样性的降低,平均成绩与最优成绩无限接近,此时便可认为算法收敛,学习结束.

3 算例分析

引入4道经典算例,连续进行10次计算,统计计算结果并以前人的研究成果作为评判标准,验证TLBO 在边坡圆弧临界滑动面搜索中的可行性.此外,设置相同的学生数量(本文设n=30,原因详见第4节),使不同边坡的滑面搜索问题可以通过学习次数来大致估计运行时间的相对大小,方便后续进行对比分析;搜索范围应具有一定的广度或者参考其他文献设置,以保证最优解包含其中.

3.1 算例1

引用文献[4]的多级均质边坡实例,其边坡断面形式和材料参数如图1所示.设置搜索范围为:xs∈[20,85],xe∈[95,200],yo∈[65,200](单位:m).

图1 算例1边坡断面及材料参数

TLBO 算法所得答案稳定在1.0362(见表1),与文献[4]采用遗传算法求解出的答案(1.036～1.041)基本一致,说明TLBO 能够应对这种边坡级数多,且范围广的均质边坡滑动面搜索问题.

表1 算例1计算结果

图2为TLBO 程序单次运行的迭代图,可以看出虽然学生群体的平均成绩在60次学习后才开始稳定,但是实际上最优成绩早已出现,展现了TLBO 算法强大的全局寻优能力.

图2 算例1迭代图

3.2 算例2

算例2为澳大利亚计算机应用协会(ACADS)的经典考核题1(c)[16],边坡断面图和土层材料参数如图3所示,ACADS推荐的裁判答案为:1.385～1.406.

图3 算例2边坡断面及材料参数

计算算例2时,滑动面各变量取值范围为:xs∈[-10,4],xe∈[-18,40],yo∈[10,50](单位:m).表2为TLBO 程序连续运行10次的计算结果,安全系数1.4032 在ACADS 推荐的裁判答案内,可见TLBO 算法能够成功捕捉非均质边坡的临界滑动面.

表2 算例2计算结果

图4为某次运算的迭代图,可知在15次学习后结果便开始收敛,表明TLBO 面对具有多个极值点的非凸优化问题也能够展现出良好的搜索效率.

图4 算例2迭代图

3.3 算例3

某海堤边坡,其剖面和各土层材料物理力学参数如图5所示.采取文献[17]中设置的变量搜索范围:xs∈[-6,2],xe∈[18,33],yo∈[6,30](单位:m).

图5 海堤边坡剖面图及材料参数

由表3可知,最小安全系数在1.7170至1.7275之间,与文献[17]中的最小计算结果1.727 基本一致;由图6可知,面对具有水平软弱夹层的土层环境,算法搜索依旧迅速.进一步说明了TLBO 算法具有较高精度的捕捉能力.

表3 海堤边坡计算结果

图6 海堤边坡迭代图

3.4 算例4

算例4是具有多个水平层带的非均质边坡,且边坡的横纵跨度很大,如图7所示.鉴于TLBO 在前述3个算例中的良好表现,该例的优化空间选取为文献[17]设置的3组搜索范围的并集,即xs∈[20,60],xe∈[170,200],yo∈[95,340](单位:m).

图7 算例4边坡断面及材料参数

表4统计的计算结果显示,临界滑动面的控制点位置xs、xe、yo大约分别在40、184、139m 左右,相比文献[17](xs、xe、yo大约分别在34、189、137m 左右),其位置偏差很大,但是对应的安全系数却小于其最优结果1.446,说明TLBO 算法可靠有效,且寻优效果更佳.图8为算例4某次计算的迭代图,学习次数k=22时,算法收敛,且收敛迅速.综合其表现,说明TLBO 算法在应对模型范围广的复杂边坡圆弧临界滑动面搜索问题时,计算速度快,且不易陷入局部收敛当中.

表4 算例4计算结果

图8 算例4迭代图

3.5 小结

本节依据边坡模型搜索范围的广度和土层结构的复杂程度,选取了4道算例,并成功应用TLBO 算法完成对其圆弧临界滑动面的求解,且在相同的学生数量下,最优解出现所需的迭代次数并没有随计算环境复杂度的增加而增加,说明TLBO 算法的信息处理能力完全能够胜任不同边坡的临界滑动面搜索问题.但是,仍有2处不足需要考究:其一,本文变量的设计对于多级边坡而言并不合理,因为它约束了滑移线剪出口和剪入口的范围,致使剪出范围不可能是剪入区,剪入范围不可能是剪出区,而这种模型内范围的分配能否包含住最优解是有待商榷的;其二,对比算例1和算例4的迭代图可知,虽然最优解出现的都很快,但是要达到收敛条件,多级均质边坡却要花费更多的时间,因此能否设计一个更好的收敛判据也是一个值得研究的问题.

4 群体规模

班级学生数量n是TLBO 算法中的唯一参数,从理论上讲,其取值的大小必定会影响到计算的结果.以n=2的极端取值情况为例,显然两位学员的相互学习可视为一种局部搜索,而标准TLBO 算法并不具备类似遗传算法跳出局部搜索的能力,因此大概率是无法得到可靠解的.TLBO 算法最出众的是其共享信息的能力,所以初始群体规模越大包含的信息量就越丰富,算法的运算成功率就越高.但是,这是否就能够说明群体规模越大越好呢?

为解决上述遗留问题,对第3节中最复杂的算例4依次完成n=2、10、20、30、40、80条件下的20次程序运行,统计其成功率和最大运算时间于表5中.结果显示:随着群体规模的增大,成功率和最大运算时间都呈现上升的趋势.综上所述,从成功率和运算时间方面综合考虑,群体规模并不是越大越好,而本文取n=30是较为合理的.

表5 程序在不同群体规模下的运行情况

5 结论

1)利用TLBO 算法分别对多级均质边坡、斜折线分层土坡、含水平软弱夹层和具有大范围多级水平层带的非均质边坡进行边坡稳定性分析,与前人的研究方法和结果对比,本文方法无需微调参数,且能够搜索出安全系数和临界滑面位置都相近的满意结果,或者安全系数更小的、位置更危险的最优解.可见在复杂边坡圆弧临界滑动面搜索问题中,TLBO 算法有着广阔的应用前景.

2)扩展了“破弧”问题的定义范围,并依据TLBO算法的特点,设计了合理的解决“破弧”问题的方案,成功避免了更多无意义圆弧的产生,优化了算法程序的执行效率.

3)从统计的计算结果来看,多次计算所得的安全系数基本相同,但变量值xs、xe、yo却在局部范围内波动.这种现象在非均质边坡中尤为明显,侧面印证了稳定系数函数是比较复杂的,在最优解附近有多个相近的峰值.