一类受媒体报道滞后性影响的传染病模型

阳丽君，班相函，王文龙

(东北林业大学 理学院，黑龙江 哈尔滨 150006)

古往今来，传染病一直是人类的重大威胁之一.1937年，Kermack和McKendrick在研究黑死病时创新性地提出了SIR仓室模型[1]，为后人研究传染病传播规律指明了方向.此后，众多国内外学者根据不同传染病的病症差异、治疗措施、传播过程建立了许多经典模型，如面对具有潜伏期的传染病，建立了SEIR模型[2-3]；面对需采取隔离治疗措施的传染病，建立了SIQS模型[4]；面对会二次感染的传染病，建立了SIRS模型[5-6]等.随着网络的普及，实现了通过电视报道、公众号、手机App等途径实时更新消息，并向公众宣传有关传染病的健康知识和预防措施，以提高公众安全意识，并直接降低传染病的传染率.因此,研究媒体报道对传染病防治的影响具有重大意义.目前有很多研究已经取得一些成果，如文献[7-8]研究了一类接种率受媒体报道影响的传染病模型，研究表明通过媒体报道来提高公众意识有利于传染病的控制.文献[9]提出用一类具有非线性发生率的传染病模型来描述当感染者数量超过阈值时媒体报道的效果，说明合适的阈值和控制强度可以阻止传染病爆发.文献[10]针对具有一定免疫水平的人群，建立了具有媒体报道和无症状感染特点的SQEIAR模型，推导出了最优媒体报道策略和检疫策略.文献[11-14]引入了不同形式的传播率，探索媒体报道对传染病的抑制作用.

上述提到的文献中大部分都没有考虑到时滞产生的影响.事实上，媒体在信息收集上就产生了滞后性，从媒体开始报道到产生积极影响需要一段时间，t时刻媒体报道的感染者数量实际是t-τ时刻的感染者数量；因此，在传染病模型中考虑时滞更加贴合实际.基于文献[14]中染病者数量达到临界值，即媒体影响因子函数为e-M(t)的情况，考虑媒体报道的滞后性，本文建立如下传染病模型：

(1)

满足的初始条件：S(0)>0,I(0)≥0,M(0)≥0;S(t)+I(t)=N(t).

将媒体报道信息量M(t)看作独立仓室，人群划分成易感者S(t)和染病者I(t)，N(t)表示在t时刻的总人口数目，Λ表示人口的常数输入率，β表示传染率，μ表示自然死亡率，γ表示疾病的恢复率，σ表示染病者数量对媒体报道的影响率，θ表示媒体报道的衰减率，τ表示媒体对病情报道的时间滞后，所有参数值均为正数.

1 基本再生数和平衡点的存在性

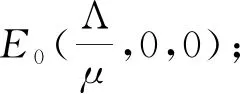
2 模型的稳定性分析

2.1 无病平衡点的稳定性

定理1无病平衡点E0的稳定性与τ无关.当R<1时，无病平衡点E0是局部渐近稳定的；当R>1时，E0是不稳定的.

证明将系统(1)在无病平衡点E0处进行线性化：

其中，Z(t)=(S(t)，I(t)，M(t))T，Z(t-τ)=(S(t-τ)，I(t-τ)，M(t-τ))T，

得到如下式子：

(2)

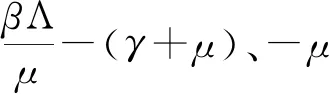
2.2 地方病平衡点的稳定性

当R>1时，系统(1)存在地方病平衡点E*(S*,I*,M*)，接下来分析地方病平衡点的稳定性.

2.2.1τ=0时地方病平衡点的稳定性

定理2τ=0时，若满足条件γ+μ>-e-M*β(I*-S*)，则地方病平衡点E*是局部渐近稳定的.

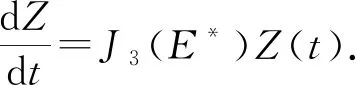
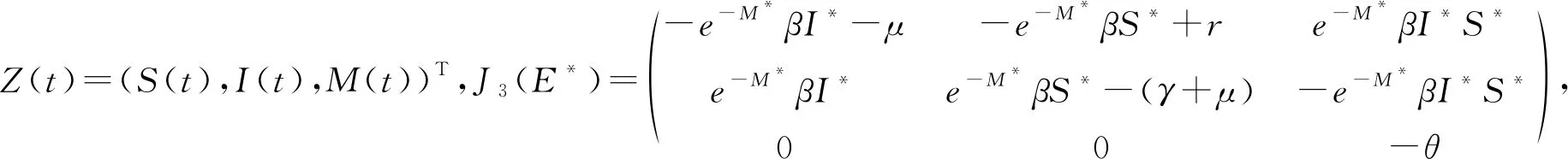
得到特征方程如下：

(λ+θ)(λ2+a1λ+a2)=0，

(3)

显然，特征方程(3)的1个特征值为λ=-θ，其他2个特征值满足方程：

λ2+a1λ+a2=0，

(4)

其中，a1=e-M*β(I*-S*)+γ+2μ，a2=μ(μ+γ)+μe-M*β(I*-S*).

当参数满足γ+μ>-e-M*β(I*-S*)，且已知μ>0，易得方程(4)的系数a1、a2均大于0.根据Routh-Hurwitz判据，式(4)所有值均具有负实部，故特征方程(3)所有的特征值均具有负实部，因此，地方病平衡点E*是局部渐近稳定的.证毕.

2.2.2τ>0时地方病平衡点的稳定性 将系统在地方病平衡点E*处进行线性化：

其中，Z(t)=(S(t)，I(t)，M(t))T，Z(t-τ)=(S(t-τ)，I(t-τ)，M(t-τ))T，

得到特征方程如下：

(λ+μ)(λ2+q1λ+q2+q3e-λτ)=0，

(5)

显然，特征方程(5)的1个特征值为λ=-μ，其余特征值需满足方程：

λ2+q1λ+q2+q3e-λτ=0，

(6)

其中，q1=e-M*β(I*-S*)+γ+θ+μ，q2=e-M*β(I*-S*)+γθ+θ+μθ，q3=σe-M*βI*S*.

定理3若满足条件|θ2(e-M*β(I*-S*)+γ+u)2|<|(σe-M*βI*S*)2|，则式(6)存在1对纯虚根λ=±iω.

证明令λ=iω，代入式(6)，分离实部和虚部可得到

(7)

将式(7)两端平方相加得

(8)

令z=ω2,则方程(8)等价于

H(z)=z2+b1z+b2=0，

(9)

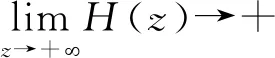
不妨设方程(9)存在1个正根为zk，k=1,2,…l，l∈N，解得

定义τ*=min{τk|k=1,2,…,l,l∈N}，因此，若满足条件|θ2(e-M*β(I*-S*)+γ+u)2|<|(σe-M*βI*S*)2|，式(6)在τk处存在1对纯虚根.证毕.

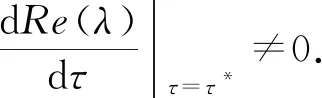
证明对式(6)求导得

整理后得到式子如下：

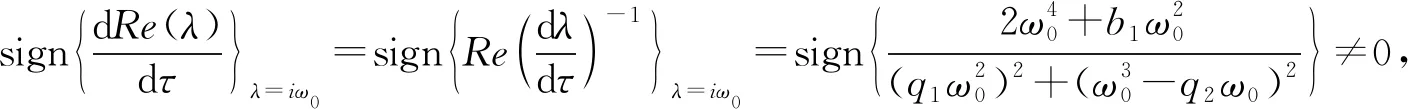
根据定理3和定理4得到如下结论：

定理5R>1时，若满足条件|θ2(e-M*β(I*-S*)+γ+u)2|<|(σe-M*βI*S*)2|，系统(1)存在地方病平衡点E*，当τ<τ*时，系统(1)的地方病平衡点E*是局部渐近稳定的；当τ>τ*时，地方病平衡点E*的稳定性发生改变，由稳定变为不稳定，且在τ=τ*处产生Hopf分支.

3 数值模拟

选取参数Λ=0.7，β=0.2，μ=0.2，γ=0.6，σ=0.3，θ=0.4，τ=2.计算得出R=0.875<1,E0(3.5,0,0).根据定理1可知，无病平衡点E0是局部渐近稳定的，如图1所示.

选取参数Λ=1，β=0.4，μ=0.1，γ=0.5，σ=0.3，θ=0.4，τ=2.计算得出R=6.666 7>1，E0(10,0,0).根据定理1可知，无病平衡点E0是不稳定的，如图2所示.

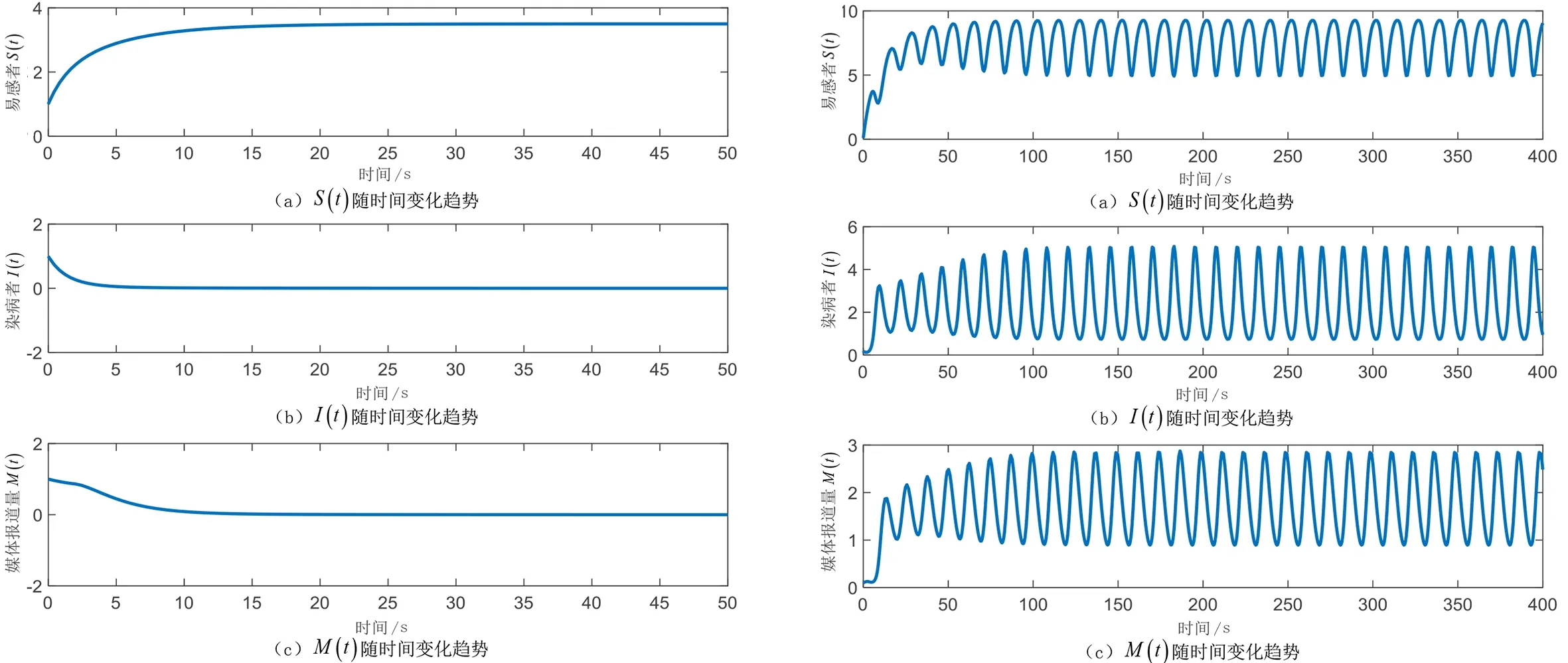
图1 R<1时无病平衡点稳定 图2 R>1时无病平衡点出现周期解 Fig.1 The stability of disease-free equilibrium when R<1Fig.2 The periodic solution of disease-free equilibrium when R>1

选取参数Λ=1.4，β=0.3，μ=0.2，γ=0.4，σ=0.2，θ=0.3，τ=0.此时计算得出R=3.5>1，E*(5.486 3,1.513 7,1.009 1).根据定理2可知，地方病平衡点E*是局部渐近稳定的，如图3所示.

选取参数Λ=1.4，β=0.3，μ=0.2，γ=0.4，σ=0.2，θ=0.3.此时计算得出临界值τ*=3.1953，R=3.5，E*(5.486 3,1.513 7,1.009 1).取τ=3.1<τ*，根据定理5可知，地方病平衡点E*是局部渐近稳定的，如图4所示.

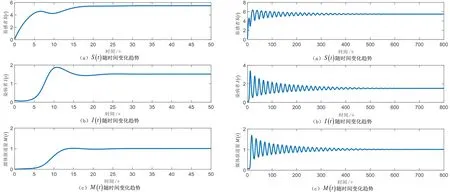
图3 τ=0时地方病平衡点稳定 图4 τ<τ*时地方病平衡点稳定

取τ=3.4>τ*，根据定理5可知，地方病平衡点E*是不稳定的，出现周期性震荡，如图5和图6所示.

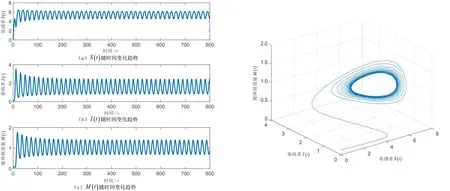
图5 τ>τ*时地方病平衡点产生周期震荡图6 τ>τ*时系统(1)出现周期解

4 结语

本文研究了媒体延迟报道对传染病传播的影响，建立了一类具有媒体报道滞后性的时滞传染病模型，探究了系统(1)无病平衡点和地方病平衡点的稳定性.结果表明，系统(1)的无病平衡点局部渐近稳定，意味着随着时间的推演，疾病最终会被消灭.同时，系统(1)的地方病平衡点在时滞τ较小时，处于稳定状态，此时可以对疾病进行有效的预测和控制；然而，随着时滞τ的增大且超过临界值时，系统(1)产生周期解，由稳定变得不稳定，易感者和染病者的群体数量产生周期震荡，这不利于对传染病的预测和控制.因此,在实际考虑媒体报道对传染病的影响时，媒体报道时间的滞后性不容忽视.

另外，媒体报道对传染病防治的影响较大，将媒体报道的信息量看作独立仓室，更细致严谨地研究媒体报道与染病者的关系是很有意义的.并且，媒体也应该将信息报道的时间延迟尽量减小,从而最大限度地帮助控制传染病的传播.