“离散数学”课程思政教案设计

管红娇，马 宾，杨美红

（1.齐鲁工业大学〔山东省科学院〕 a.计算学部；b.山东省计算中心〔国家超级计算济南中心〕，山东 济南 250353；2.山东省计算机网络重点实验室，山东 济南 250353）

一、课程思政的背景

课程思政是指教学活动在确保教学任务和教学目标的基础上，以教学内容为载体，自然融入德育元素，提升学生知识水平的同时，培养优良习惯和态度，建立正确的价值观，达到价值塑造、能力培养、知识传授三位一体的教学目标［1］。

2016年，习近平总书记在全国高校思想政治工作会议上指出，要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人，努力开创我国高等教育事业发展新局面［2］。2017年，中共中央、国务院印发《关于加强和改进新形势下高校思想政治工作的意见》，提出坚持全员全过程全方位育人（简称“三全育人”）的要求［3］。2020年，教育部印发的《高等学校课程思政建设指导纲要》指出，全面推进课程思政建设是落实立德树人根本任务的战略举措［4］。因此，课程是实现将思想政治教育贯穿教育教学全过程的主阵地，课程思政是把立德树人融入大学课堂的重要手段和途径［5］。

二、“离散数学”课程特点与课程思政要求相统一

“离散数学”是计算机科学与技术、软件工程、网络空间安全等专业的基础课程，研究离散量的结构及相互关系，是现代数学的重要分支，主要包括数理逻辑、集合论、图论和代数结构等内容。“离散数学”是数学类课程与计算机类课程的过渡，旨在培养学生利用数学语言或形式化的符号系统对自然世界进行抽象表达、解决实际问题的能力，为后续学习“数字电路”“操作系统”“数据结构”“数据库原理”“计算机网络”和“编译原理”等专业课程，以及“人工智能”“物联网”“区块链”“大数据”等交叉学科课程奠定坚实的数学基础［6］。

“离散数学”一般开设在大二上学期，此时已经修完“高等数学”“线性代数”“概率论”等基础理论课程，且有些内容在高中阶段已经学过，比如集合和函数。但是，在教学过程中，一些学生反映这门课学起来有点吃力，主要是概念和定理等不易理解，不知如何运用所学知识解决具体问题。一个原因是“离散数学”中部分内容对以前高中内容进行了系统深化和提升，如二元关系是函数的泛化表达；另一个原因是课程概念繁多，公式、定理等比较抽象，需要学生具有抽象思维能力、归纳构造能力和逻辑推理能力［7］。

课程思政要结合所授课程的特点，立足于专业课程中的文化基因和价值范式，提炼出其中蕴含的思政元素。比如，结合社会热点或学术科研，把德育元素合理融入教学内容，促进学生对知识点的理解，提高学生利用所学知识解决实际问题或学术问题的能力，或者利用接近学生生活的案例增加教学趣味性，提高学生主动思考的能力。因此，课程思政可以通过增加价值导向的案例改变“离散数学”课程晦涩难懂、教学效果不佳的现状，实现专业教育与思想政治教育和谐统一。

三、思政元素挖掘

“离散数学”是典型的以数学符号等形式化语言为主、以数学方法进行逻辑推理的课程。作为形式科学，数学绝大部分内容是基本概念、基本定理、基本方法，是对自然界和人类社会内在规律的探究和总结，因此具有抽象性、客观性、严谨性和批判性，体现了马克思主义基本原理中的辩证唯物主义思想［8］。

抽象是数学难以理解的根源，而抽象也恰是数学的美妙之处。抽象是归纳事物或事物间联系的规律，描述事物发展本质的过程，是从知识上升到观点、思想的工具和桥梁。本文教案设计重点突出抽象思维的重要性。

四、教案设计

（一）目标要求

以耿素云等编著的《离散数学（第五版）》为参考教材，以第五章《图的基本概念》中结点度数为例，介绍融入课程思政元素的教案设计。目标要求主要包括以下三方面。知识目标：理解无向图中结点度数的定义。能力目标：能够通过图的邻接矩阵计算结点度数。德育目标：培养抽象表达能力和计算思维。

（二）课程导入

给出“东数西算”工程算力网络的图示，由图中数据中心集群是整个算力网络中的关键枢纽，引出结点度数的概念。

2022年2月，“东数西算”工程正式全面启动，跟“西电东送”与“西气东输”工程类似，“东数西算”工程将东部算力需求引导到西部。在该算力网络中，有10个国家数据中心集群，而2019年的数据统计，中国约有7.4万个数据中心。也就是说，上万的数据中心要通过10个中心集群进行数据处理和传输，可见作为关键结点的中心集群的重要性。描述关键结点重要性的一个指标是结点度数，是本节课要介绍的内容。

以“东数西算”工程为背景，引入本节的授课内容，能够增加学生的学习兴趣，同时提升学生的民族自豪感和自信心。

（三）新课讲授

定义。由“东数西算”工程算力网络抽象出无向图，通过直观感受数据中心集群与数据中心的重要性差异，引出描述该差异的一个指标，即结点度数，继而给出其数学上的严谨定义：在无向图中，顶点v作为边的端点的次数之和称为v的度数，简称度，记作d（v）。也就是，顶点v关联的边的条数就是度数。

从“东数西算”工程算力网络到无向图，是现实世界到信息世界的第一层抽象，把算力网络中的数据中心集群抽象为无向图中的结点，把数据中心集群间的数据传输（联系）抽象为无向图中结点间的边。抛去数据中心集群具体的含义，无向图体现了事物间的本质联系。

邻接矩阵。给出无向图后，通过数数方式可以得到每个结点的度数，如果有成千上万个结点，如何快速准确得知结点度数是需要解决的问题。计算机擅长做重复的机械运算，怎样用计算机描述无向图，如何将无向图从信息世界抽象到计算机世界？矩阵是将无向图从信息世界抽象到计算机世界的工具，这里介绍的是邻接矩阵。邻接矩阵中元素表示每个结点与其他结点连接的边的条数，所以第i个结点的度数是邻接矩阵中第i行或第i列的元素之和。

从无向图到邻接矩阵是信息世界到计算机世界的第二层抽象，邻接矩阵的行数和列数是无向图中结点的个数，而结点间的边数用两个结点对应的矩阵元素值表示。通过两层抽象可以将现实世界中对算力网络的优化、资源配置与管理等问题转化为基于矩阵的计算与分析。使用计算机或者数学工具矩阵处理自然界或人类社会中的实际问题，体现了抽象思维的重要性。本节授课内容和两层抽象如图1所示。

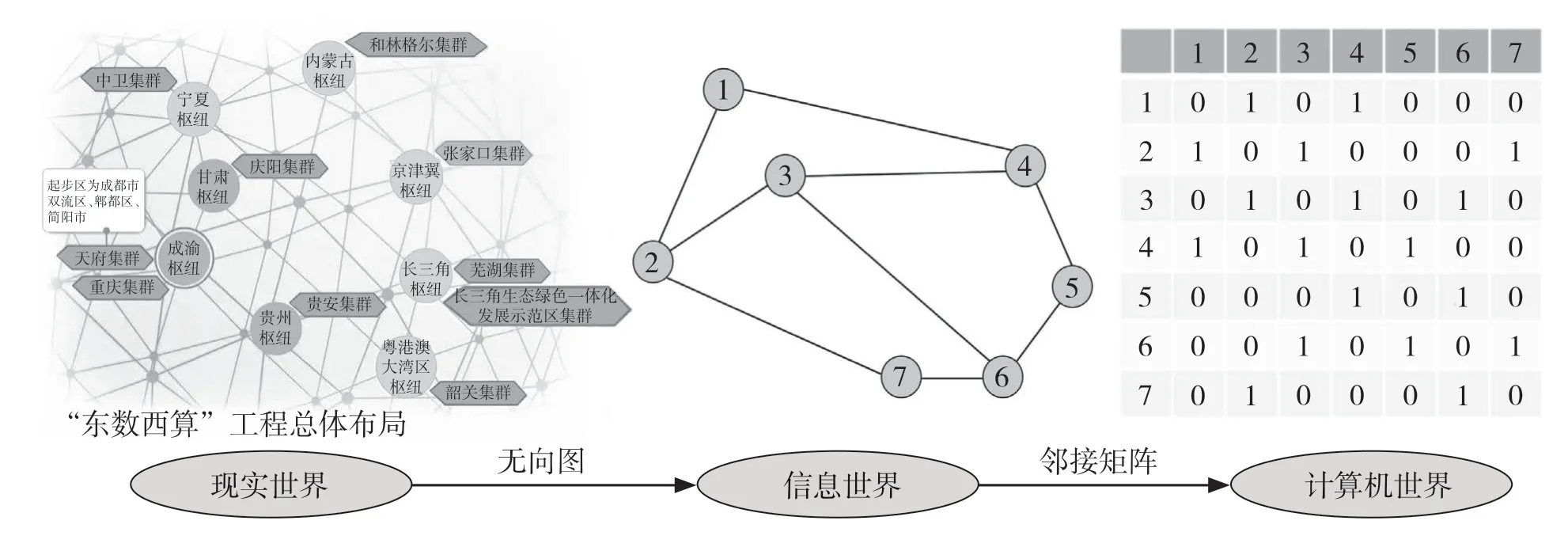
图1 主要授课内容和两层抽象

（四）测评与小结

给出例题检测学生学习效果，体会并深刻理解数学抽象的意义。总结本节课的主要内容，便于学生把握本节内容的整体结构和重点难点。布置作业，使学生及时巩固并消化课堂知识，做到“学而时习之”。

结语

本教案设计以“离散数学”中“无向图的结点度数”为授课内容，重点突出数学抽象的思政元素，引导学生理解抽象思维在解决实际问题中的重要性，增加了课堂内容的生动性和深刻性，使学生在学习知识的同时，获得对生活更深的认知和思考，有“余音绕梁”的回味。德育元素的渗透也契合了课程“培养抽象表达能力和计算思维”的目标要求，因此，本文的教案设计提供了以教学内容为载体，自然融入德育元素，实现课程思政的一种方式。“离散数学”课程受众面广，且处于专业核心课程地位，在课程中融入思想政治教育，能够得到师生的重视，教师在“授业解惑”的同时，通过“传道”为学生树立正确的价值观。课程教案设计融入德育元素，是推行“德融课堂”的重要组成部分，也为其他院校开展相关课程思政改革提供了可参考范本。