翼型边界层脉动压力统计特征分析
2023-01-05魏斌斌高永卫昔华倩
魏斌斌,高永卫,孙 博,昔华倩,邓 磊
(西北工业大学航空学院,西安 710072)
0 引言
流动转捩决定了边界层流态,对飞行器气动特性有重要影响,其一直是研究的难点和热点。
边界层转捩过程包括几个不同特征的阶段:1)感受性阶段:在这个阶段自由流中的扰动以某种途径触发了边界层中相应的扰动;2)扰动的演化:这个阶段包括扰动的线性和非线性演化,线性演化过程中,不同的波独自演化,非线性演化阶段,波与波之间、波与自由流之间都会相互影响;3)转捩段:在这个阶段扰动幅值急剧增大,频谱急剧变宽,层流剖面迅速转变为湍流剖面。在转捩过程中,伴随着壁面摩擦应力、温度、压力脉动等特征的急剧变化,通过对这些特征进行检测可实现边界层转捩探测;根据测量特征不同,边界层转捩探测技术也不同[1]。
在边界层转捩探测实验中,常用的实验方法有热学方法(热线风速仪法、温敏涂料法、热膜技术等)、流动显示技术和脉动压力技术等。
在静态实验中,人们就转捩开展了大量研究。早在20世纪70年代,Knapp等[2]和Lagraff[3]就利用热线方法研究了亚声速和高超声速边界层转捩。Costantini等[4]使用温度敏感涂料研究了非绝热表面对转捩的影响。Fey等[5]使用温敏漆在低温风洞中对高雷诺数下的转捩进行了探测。Hodson等[6]和Zhang等[7]通过热膜输出电压与壁面剪应力的关系,进一步定义了准壁面剪应力。Burgmann等[8]使用TR-PIV方法对层流分离泡的发展特性开展了流动显示实验,研究了Kelvin-Helmholtz不稳定性对分离泡的影响。
同时,翼型在俯仰振动过程中的非定常转捩特性也越来越受人们的重视。Lee等[9-10]利用热膜传感器研究了NACA0012翼型在振荡过程中的转捩和失速特征。Richter等[11]利用热膜技术研究了EDI-M109翼型的非定常转捩特性。Kim等[12]借助热膜和烟流研究了雷诺数对振荡NACA0012翼型非定常边界层的影响。Haghiri等[13]使用热膜技术对做俯仰振动运动的SC(2)-0410翼型进行了转捩探测实验,研究了压缩性、缩减频率等对转捩的影响。Ikami等[14]使用结合了温敏涂料和碳纳米管的流动显示技术对俯仰振荡翼型的转捩进行了探测,研究了转捩/再层流化的迟滞效应。
以上方法在实际应用方面仍存在一定限制。与上述实验技术相比,使用脉动压力传感器对边界层转捩进行检测更为方便实用。这得益于脉动压力传感器集成度越来越高,小型化越来越成熟,响应越来越快,且测控设备的响应也越来越快。早在20世纪70年代,Heller[15]就利用声学技术探测到了高超声速再入飞行器上的流动转捩。Lewis和Banner[16]使用脉动压力测量技术研究了X-15垂尾的边界层转捩。本文团队在使用脉动压力进行转捩探测方面也开展了大量的研究工作[17-20]。在使用脉动压力方法进行转捩探测时,一个基本的判据是转捩处的脉动压力均方根值(root mean square,RMS)相较于层流和湍流有峰值。出现这一现象是因为转捩处伴随着扰动的非线性增长,使得压力脉动急剧变化,带来显著的RMS值增加。
通过对翼型边界层内脉动压力或者脉动速度的测量,可获得不同流态的脉动信息时间序列。使用该时间序列的概率密度分布函数(probability density function,PDF)可以很容易地计算出一些反映转捩的统计量,比如脉动压力RMS。脉动压力RMS判据能够有效地对转捩位置进行判断,然而,该判据只利用了边界层脉动压力信息这一个统计特征,丢失了包括偏度、陡度等在内的大部分统计特征,更没有考虑其时序特征。
除了使用脉动压力RMS判据,也有人使用脉动速度的PDF形态进行转捩判断。王凯利等[21]使用热膜对平板边界层的Klebanoff型转捩进行了探测,得到了不同雷诺数下的脉动速度时间序列及其对应的PDF,给出了不同流动形态下脉动速度PDF的形态。他们认为通过识别PDF形态可准确识别转捩位置。后来,郑国锋[22]给出了湍流度ε =1.5%情况下的平板边界层不同流态脉动速度的PDF,他们发现这时转捩处的PDF失去了文献[21]中描述的变化规律,也就无法进行转捩判断。
本文使用脉动压力方法对翼型边界层进行转捩探测,深入研究了自然转捩情况下翼型边界层不同流态的脉动压力统计特征,包括均方根值σ、偏度s、陡度k和信息熵I;首次绘制了不同流态的(s,k)相图,并详细推导了I与σ、s、k之间的数学关系,建立了I与σ、s、k之间的显式表达,将用于转捩判断的一维决策空间(σ)扩展为了四维决策空间(σ,s,k,I)。
1 方法
1.1 实验设置
本文实验在西北工业大学的NF-3风洞进行。NF-3风洞是亚洲最大的低速翼型风洞,实验段尺寸为8.0 m×1.6 m×3.0 m(长×高×宽),最大风速为U =130 m/s,湍流度不大于0.045%,基于弦长的实验雷诺数可达7×106。
实验模型和测压点布置如图1所示。翼型模型弦长c =600 mm。在模型中剖面(z/l =0.50)布置25个Kulite XCQ-093压力传感器。为了研究不同边界层流态(层流、转捩和湍流)的脉动压力特性,将实验采样率设置为fs= 20 kHz,以确保足够高的时间精度。

图1 翼型和测压点Fig.1 Airfoil and pressure measurement points
通过调整风速来改变雷诺数,本文实验基于弦长的雷诺数为Re =0.8×106、1.1×106、2.0×106。实验的迎角范围为α =0°~8°,迎角间隔为Δα=1°。本文所有实验均是自然转捩状态。
1.2 计算方法
本文研究不同边界层流态的脉动压力特性,包括其统计特性和信息熵。统计特性里面,本文研究了脉动压力的均方根值σ、偏斜度s和陡峭度k,计算方法如式(1)所示。偏斜度和陡峭度衡量了脉动压力概率密度分布偏离Gauss分布的程度:

式中,p是脉动压力,i是序号,N是采集数量,p是压力均值。
本文还研究了不同流态脉动压力的信息熵I(Information entropy)。信息熵的概念是Shannon于1948年提出的,他用信息熵的概念来描述信源的不确定度,计算方法如式(2)所示:

式中,P是事件xi发生的概率,n是事件个数。
对于一个均值为0的时间序列x = x(t),设其概率密度分布函数为f(x),则有以下关系式:

若考虑分布在区间[xi,xi+1]上的概率,有P(xi)=f(xi)(xi+1-xi)= f(xi)Δx。所以式(2)可以表示为:

将式(3)带入式(4),可得:

本文进一步将不同流态脉动压力的统计特性σ、s和k与式(5)中信息熵联系起来。
对g(x)=log2f(x)进行四阶Taylor展开并舍掉误差项,则有以下关系:

将式(6)带入式(5),可得:

将式(3)带入式(7),可得:

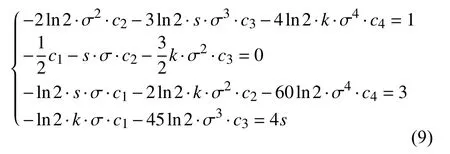
式(9)是一个线性方程组,其解如式(10)所示,详细的求解过程请参考附录A。

式(6)中,x =0时,可得c0=log2f(0)。将式(10)和c0带入式(8),可得:
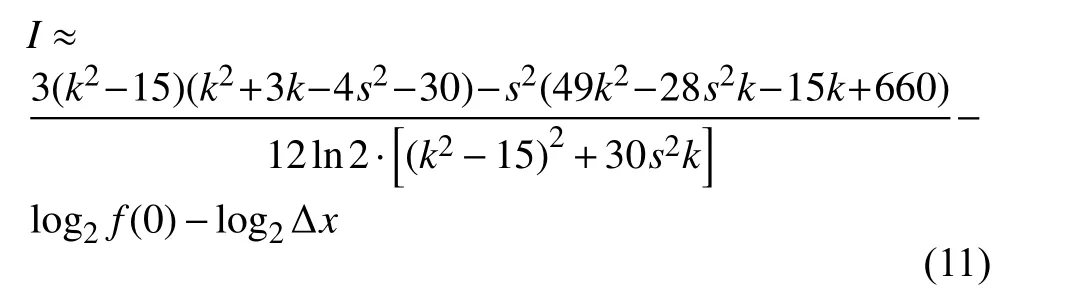
特殊情况下,对于Gauss分布,有s=0,k =3,f(0)=,式(11)变为:
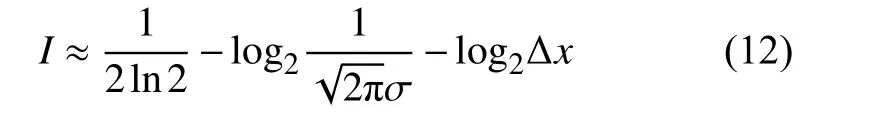
参考Gauss分布发现,式(11)中的f(0)与σ有关。在这里,不妨假设 f(0)=这时式(11)变为:
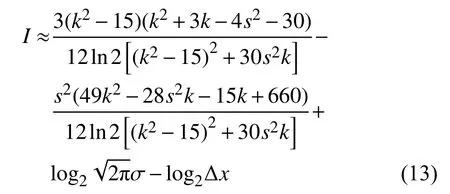
这样,本文就将信息熵I与统计量σ、s和k联系了起来。
值得注意的是,在推导式(13)的过程中,使用了两个假设:
假设一:脉动压力概率密度分布函数f(x)的对数g(x)= log2f(x)服从四阶Taylor展开形式;
假设二:脉动压力概率密度分布函数f(x)在x =0处的取值f(0)与脉动压力均方根值σ的倒数服从线性回归模型 f(0)=
这两个假设均是基于Gauss分布来考虑的。对于假设一:一个Gauss分布的概率密度分布函数f(x)的对数g(x)=log2f(x)是一个关于x的二次函数,所以,如果一个脉动压力时间序列的概率密度分布函数与Gauss分布相差不大的话,其应该也可以使用一个多项式来表达,为了精度更高,在这里我们选择了四阶Taylor展开形式。对于第二条假设:一个Gauss分布f(x)在x = 0处的取值为 f(0)=所以本文假设,脉动压力概率密度分布函数f(x)在x =0处的取值也大概服从这种关系。
2 结果与讨论
本文使用脉动压力方法对翼型边界层进行了转捩探测,研究了不同边界层流态脉动信息的统计特征。
2.1 转捩的RMS判据
在进行转捩判断时,本文使用的是成熟的脉动压力RMS判据。
以Re =1.1×106为例对数据进行分析。在Re =1.1×106和α=2°的情况下,转捩结果如图2所示,其中图2(a)是典型位置处的波形,图2(b)是不同位置处的RMS值。
可以看出,转捩位置处脉动压力的时域特性与层流和湍流中的脉动压力时域特性显著不同,即转捩区内的脉动压力振幅更大,并且表现出更明显的间歇性。在转捩过程中,由于扰动的线性演化和非线性演化,使得扰动幅值大幅增加,在这个过程中,许多物理量也会随之剧烈变化,比如壁面摩擦应力、温度、压力脉动等特征。在层流区,扰动几乎没有发展,这时传感器感受到的压力脉动呈现与白噪声接近的形态;流动发生转捩时,压力脉动会急剧变化,其幅值、频率等都会发生显著变化;转捩为湍流后,脉动压力的变化会再次平稳下来。使用脉动压力RMS转捩判据对转捩位置进行判断,即与层流和湍流相比,转捩位置的脉动压力RMS值存在峰值。该状态下,x/c =0.65位置处脉动压力存在一个RMS峰值,即x/c =0.65为转捩位置。
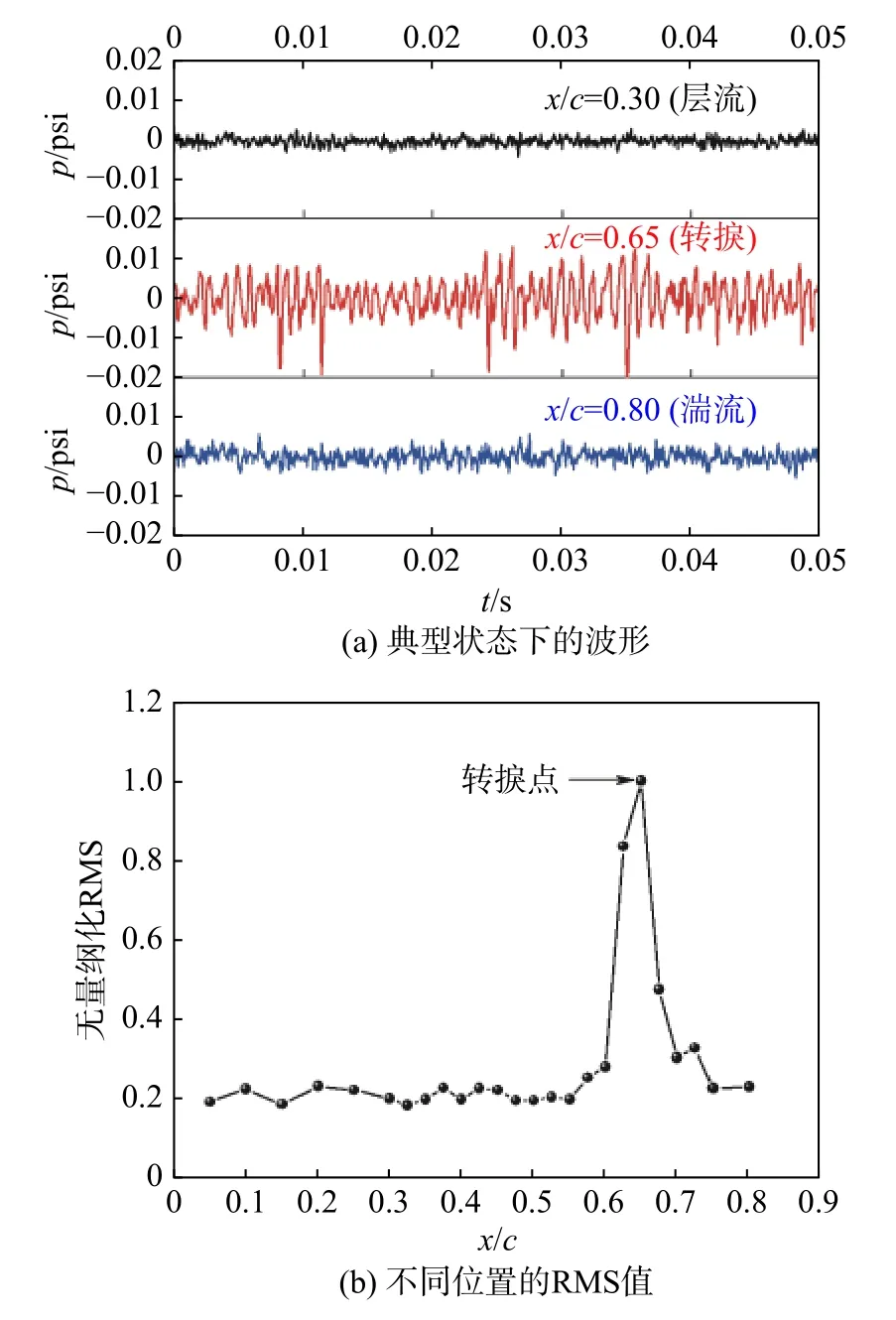
图2 迎角α = 2°情况下的转捩结果Fig.2 Transition result for the airfoil with an angle of attack at α = 2°
为了进一步验证转捩位置的准确性,本文将传统RMS判据获得的转捩位置与计算结果进行了对比,如图3所示。散点为实验结果,计算结果是eN方法[23-24]的计算结果,黑色实线为N = 8时的计算结果,红色虚线是N = 9时的计算结果。可以看出,本文实验结果与计算结果一致,说明本文实验的转捩探测结果是可靠的。
2.2 不同流态的(s,k)分布
前文介绍了转捩的RMS判据,其实脉动压力RMS值就是均方根值σ,本节对另外两个统计量—偏度s和陡度k进行讨论。
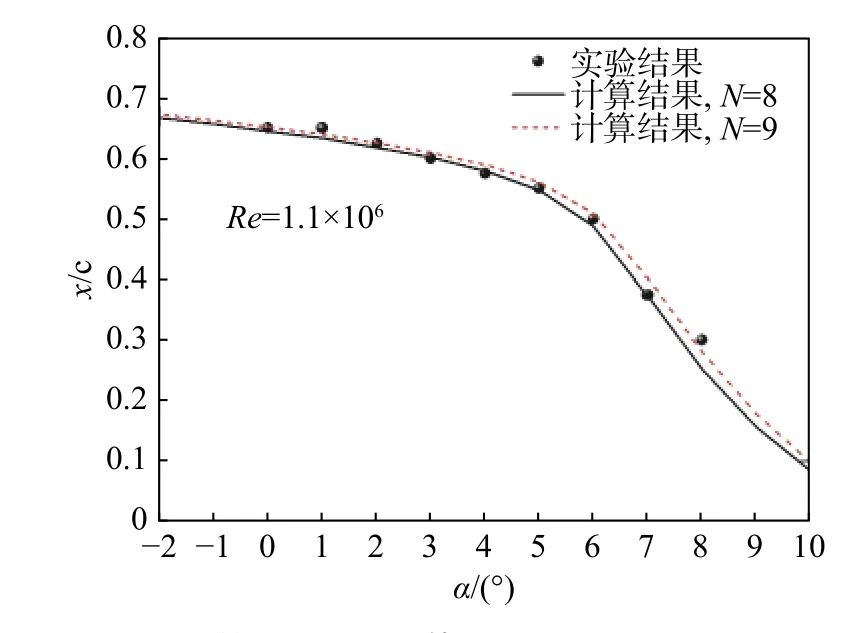
图3转捩位置的计算结果与实验结果对比Fig.3 Comparison of the transition locations between numerical and experimental data
图4 是不同雷诺数情况下偏度s和陡度k的相图(s,k)。关于翼型边界层不同流态的这种相图,就目前作者掌握的资料来看,属于首次绘制。从图4可见,就不同流态的统计量而言,不仅均方根值σ有明显区别(图2),偏度和陡度在(s,k)相图上也有显著区别。对于层流而言,其在(s,k)相图上呈现斜率更大的线性分布,接近s=0,说明层流信息的偏度几乎为0,其与Gauss分布的偏度接近;对于湍流而言,其在(s,k)相图上呈k ≈3的直线分布,其与Gauss分布的陡度接近;对于转捩而言,其在(s,k)相图上的分布较湍流更为靠下,其特征与Gauss分布相差较大。而且不同雷诺数下的分布规律基本一致。
将不同雷诺数的实验结果放在一起进行对比,如图6所示,其中图6(a)是(s,k)在直角坐标系下的相图,图6(b)是其以(0,)为原点进行极坐标转换后的极坐标相图。可见,不同流态的(s,k)分布是显著不同的,且在原点(0,)(式(13)的奇点)处没有(s,k)分布。这在一定程度上说明了翼型边界层内的脉动压力信息不会呈现s= 0、k =的统计特征。
本文首次绘制了翼型边界层不同流态脉动压力信息的(s,k)分布,分析了其在直角坐标系和极坐标下的分布特点。本文整理的数据可对研究人员建立分类模型和数据分析提供数据支持。
2.3 不同流态的信息熵
前文讨论了翼型边界层不同流态脉动压力信息的均方根值σ、偏度s和陡度k的分布,本节对其信息熵I的分布进行讨论。

图4 不同雷诺数情况下(s, k)的相图Fig.4 Phase diagram of (s, k) parameters under different Reynoldsnumbers

图5 不同雷诺数情况下(s,k)的极坐标相图Fig.5 Phase diagram of (s, k)parametersin the polar coordinate under different Reynolds numbers

图6 不同流态的(s,k)分布Fig.6 Distribution of (s, k) parametersfor different flow states
在1.2节,本文详细推导了信息熵I与均方根值σ、偏度s和陡度k的内在数学联系,本节首先对式(13)进行了验证。在推导式(13)的过程中,使用了两个假设,见1.2节。
对于假设一,以Re = 1.1×106和α=2°的情况为例进行说明。图7是不同流态(层流、转捩和湍流)脉动压力信息概率密度分布函数f的对数形式g的计算值与四阶Taylor展开拟合结果的对比。散点是对f函数求对数的实际计算结果,线条是关于g函数的四阶Taylor展开拟合结果。可见,对于不同流态而言,使用四阶Taylor展开均能对g进行精度较好的模拟,说明本文引入的第一个假设合理,计算结果可信。

图7 四阶Taylor展开验证Fig.7 Verification of the 4th-order Taylor expansion
另一方面,由图7可知,层流、湍流和转捩脉动压力信息概率密度分布函数的对数g表现出的形态有显著差异。转捩信息的g函数表现出更宽的横坐标分布,且有较大范围的“平台”区;层流信息的g函数表现出比较窄的横坐标分布,其形态更为“瘦高”;而湍流信息的g函数形态介于转捩和层流之间。
对于假设二,本文对所有实验状态的结果进行了计算,如图8所示,其中,散点是实验结果,直线是的计算结果。可见,f(0)与脉动压力均方根值σ的倒数或σ与f(0)的倒数呈显著的线性关系;且实验结果与=的直线计算结果拟合优度达到R2=0.9,说明该直线模型能较好地反映实验结果分布规律,证明本文引入的第二条假设也合理。
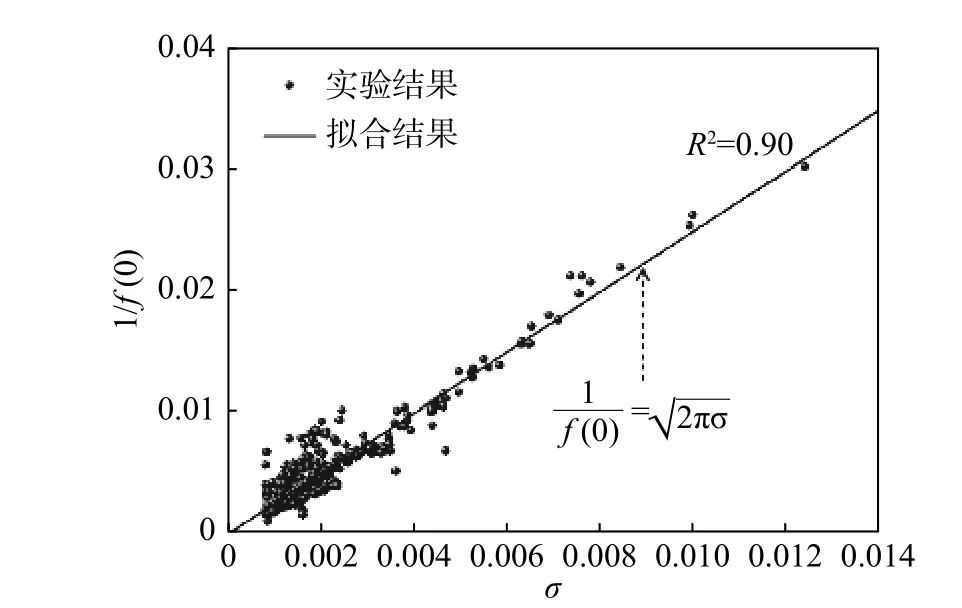
图8 线性回归模型验证Fig.8 Verification of the linear regression model
事实上,本文提出的第二点线性回归假设是基于Gauss分布思考的。对于均值为0的Gauss分布来说:

前文对本文引入的两个假设进行了详细的分析讨论,验证了假设的合理性。为了验证式(13)的正确性,只验证两个假设的正确性是不够的,需对式(13)本身进行进一步的验证。
因此,本文仍然以Re = 1.1×106为例进行说明,对式(13)进行验证,如图9所示。其中,散点是直接使用式(2)进行计算的结果,虚线和点线分别是使用式(11)和式(13)计算的结果,黑色和红色分别代表x/c = 0.475和x/c = 0.65。
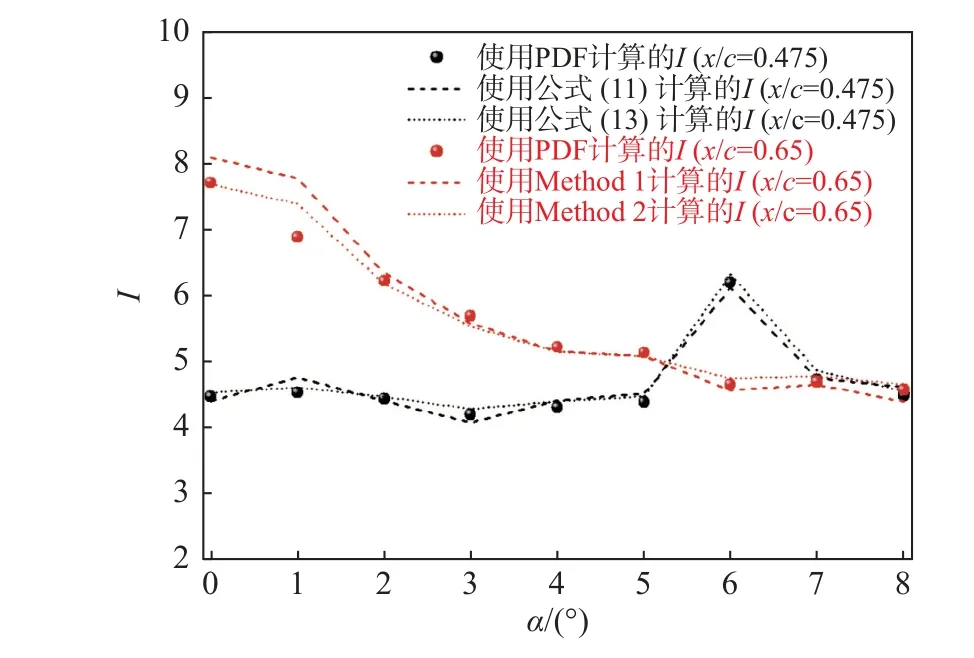
图9 不同方法计算的信息熵I比较Fig.9 Comparison of the information entropy I calculated using different methods
可见,使用本文推导的公式(11)和公式(13)对信息熵I进行计算均能得到较为准确的结果,且式(13)较式(11)能够更紧密地将I和(σ,s,k)联系起来。这也间接证明了本文引入的两个假设的正确性。另一方面,信息熵表征了一个随机变量的不确定性,该值越大表明随机变量越无序。在x/c =0.475位置处,当α =6°时信息熵最大(图9黑颜色),该位置也是α =6°时最接近转捩的位置。在x/c =0.65位置处,当α=0°时信息熵最大(图9红颜色),该位置也是α=0°时发生转捩的位置(图3)。可见,脉动压力信号的信息熵一定程度上能反映流动形态。
图10是不同流态的(s,k,I)分布,包括3-D图、俯视图、前视图和侧视图,图中的I1代表的是式(13)右边第一项,即:
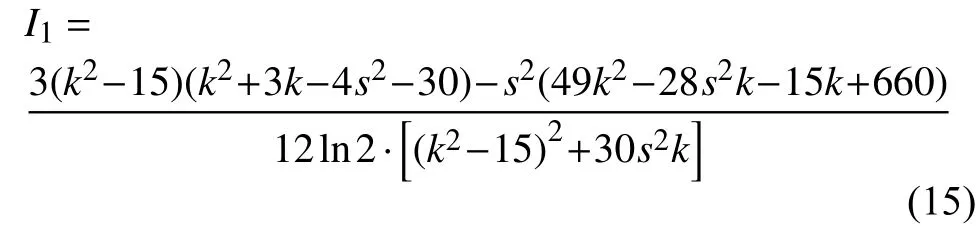
相较于图6(a),图10增加了一个维度I1。图中,蓝色散点是层流,红色散点是转捩,黑色散点是湍流。
从图10可以看出,相较于偏度s,陡度k对I1的影响更为显著,在k =的截面附近,k的微小变化会带来I1的显著变化。本文注意到,湍流特征处于k≈3的截面上(图4和图6(a)),而转捩特征位于k <3的截面上,更远离k =的截面,I1的变化更为平缓。可见相较于转捩,湍流信息的I1值变化可能会更显著。
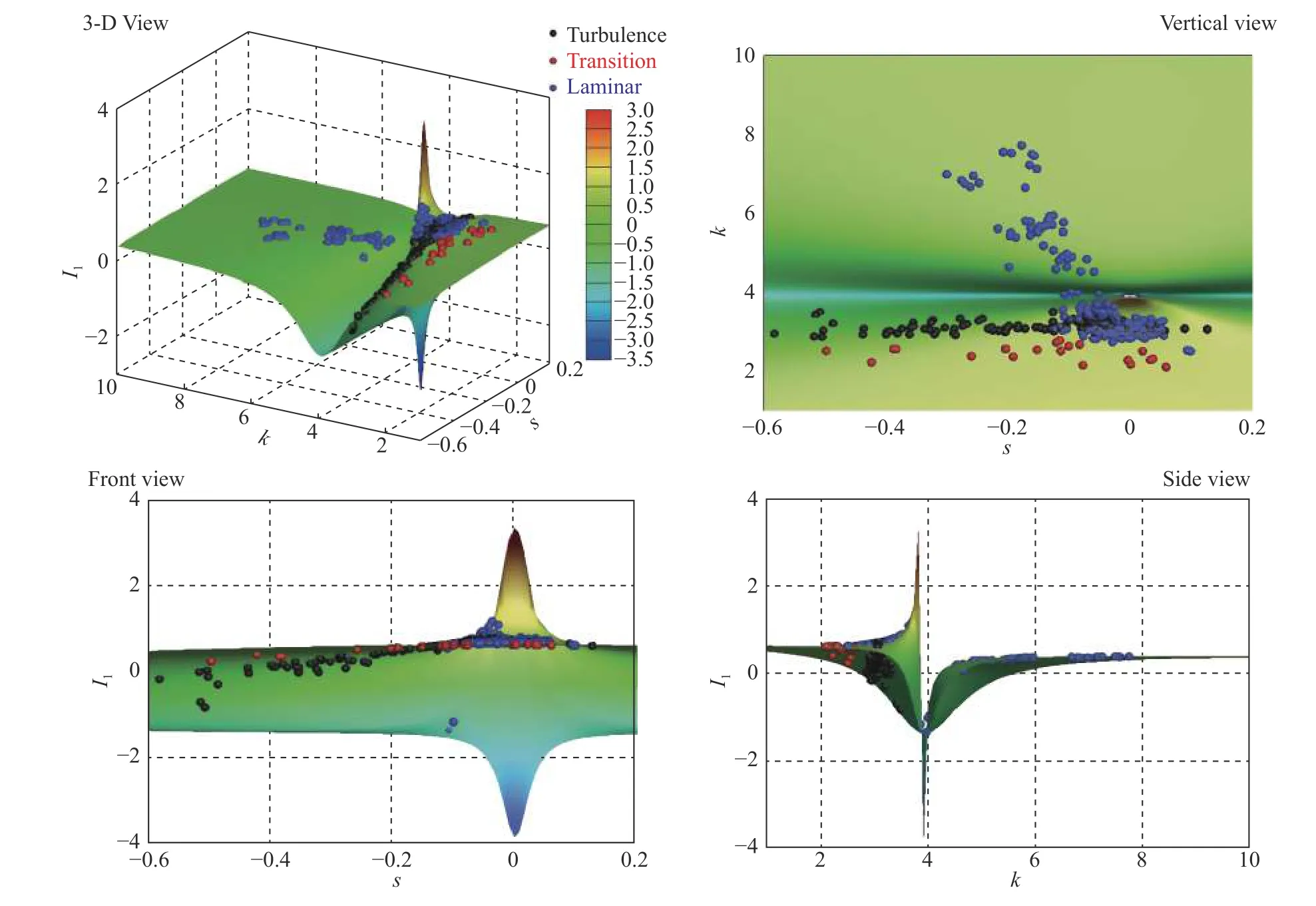
图10 不同流态的(s,k,I)分布Fig.10 Distribution of (s, k,I) parameters for different flow states
整体来看,转捩信息的I1值(式(13)右边第一项)是变化最为平缓的,这是其特征分布远离奇点所引起的。由于转捩信息的脉动压力均方根值σ是最大的,因此转捩信息对信息熵I的贡献主要体现在式(13)右边第三项log2本文推导的公式有助于人们深刻理解信息熵与一般统计量之间的内在关系。
在使用传统的基于脉动压力RMS的转捩判据进行转捩判断时,由于只使用了一个统计量σ,因此,该判据是一维的。本文将该判据扩展至四维空间(σ,s,k,I),但由于四维空间无法可视化,因此本文只呈现了四维空间(σ,s,k,I)在三维空间(s,k,I)中的投影结果,即图10。
3 结 论
本文使用脉动压力方法对翼型边界层进行了转捩探测,深入研究了自然转捩情况下翼型边界层不同流态的脉动压力统计特征,包括均方根值σ、偏度s、陡度k和信息熵I。通过绘制不同流态的(s ,k)相图进行研究,结果表明层流信息的偏度s与Gauss分布的偏度接近;湍流信息的陡度k 与Gauss分布的陡度接近;而转捩在(s,k)相图上的分布较与Gauss分布相差较大。
通过引入两条假设,详细推导了信息熵I与σ、s、k之间的数学关系,建立了I与σ、s、k之间的显式表达式,从而将传统的基于脉动压力RMS值判据的一维决策空间扩展为了由多个统计量构成的四维决策空间(σ,s,k,I)。
本文工作有助于人们深刻理解信息熵与一般统计量之间的内在关系,有助于研究人员后续的数据分析、分类模型建立以及规则提取等。
致谢:感谢NF-3风洞的杨新合、李智广、张习良和李敏芳等实验人员为本文实验付出的辛勤劳动!
附录A
正文式(9)(即式(A1))是一个线性方程组,本附录介绍正文中式(9)到式(10)的求解过程。

由式(A1)的第四个式子可得:

将式(A2)带入式(A1)的前三个等式,可得:

对于式(A3),第一个式子乘以15,第三个式子乘以k,可得:
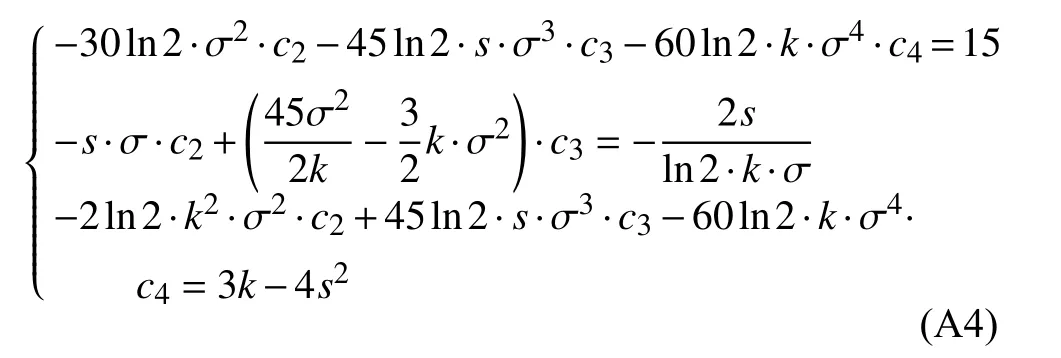
式(A4)中,第一个式子与第三个式子相减,第二个式子乘以-2k可得:

通过式(A5)可得:

将式(A6)带入式(A3)中的第一个式子,可求解出c4:
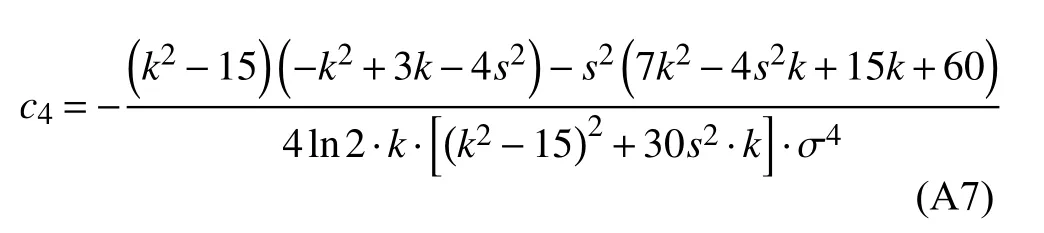
注意到正文式(8)中并没有参数c1,因此,没有对c1进行求解。至此,c2、c3和c4全部解出:

特殊地,对于Gauss分布,有s= 0,k = 3,这时,有:

