亚声速射流轴对称模态的声辐射研究

宋正旋，方一红

(天津大学机械工程学院高超空气动力学研究室，天津 300072)

0 引 言

射流噪声一直是气动声学研究的核心问题，其产生的噪声污染严重影响飞行性能，危害飞行器的使用寿命。亚声速飞行的民航客机产生的射流噪声，会对机场地面工作区和附近居民区造成巨大的噪声污染，严重影响生活。因此，研究亚声速射流噪声的机理有着重大意义。

20世纪50年代，Lighthill[1-2]创立了声类比理论，开启了气动声学研究，其后也有各种衍生理论[3-4]，它们共同构成了气动声学的经典理论。声类比理论给出了声源的模拟，但没有从物理机制上解释声源的产生和传播。Tam和Burton[5]使用了渐进匹配方法，用线性稳定性理论计算超声速模态的声辐射，开启了研究声辐射的新方法。此后，Wu团队[6-8]用临界层理论研究了超/亚声速射流的相干结构非线性演化和声辐射，对超/亚声速相干结构的噪声产生机制给出了清晰的物理解释。

Crow[9]通过多种方法研究了亚声速射流，观察拟序结构的发展，指出这些结构对声场辐射起着重要作用。Ronneberger和Ackermann[10]研究了亚声速射流中差频扰动及其声辐射，检测到非线性激发的差频扰动有很强的增长能力，且对远声场有较大贡献。

近年来，数值方法日益成熟，广泛运用于气动声场的求解。Freund等[11-12]采用DNS研究了超/亚声速圆射流的噪声产生与传播机理，结果表明亚声速射流噪声具有高方向性，与轴线成小角度。Sandham和Suponitsky等[13-14]等利用直接数值模拟方法（DNS）研究了亚声速射流不稳定波的线性与非线性演化，同样发现差频扰动有很强的增长能力，在远声场中占据主导作用。Schmidt和Towne等[15]利用大涡模拟得到了Ma=0.9湍射流的相干特性，捕获了一类新的声波，并进行了远场研究。

流场和声场的尺度不同，用直接数值方法求解是困难的，需要极大的运算能力。因此将流场和声场分别计算的混合算法更具有实用性。Wu的研究提供了一种新的声场计算方法，该方法从理论上将远场声辐射方程和近场压力扰动联系起来。郭娜、郑美香等应用Wu的方法研究了超声速射流中的声辐射特性[16-17]，给出的声辐射结果与实验吻合很好。

在此基础上，本文将采用DNS计算Ma=0.9、Re = 3600射流的轴对称模态，给出近场不稳定波的演化规律。对于声场的计算，则采用Wu的理论研究结果，从流场中提取出声源相关参数，计算并分析声辐射的强度和方向性。通过将Wu的理论与经验声场公式以及前人研究的理论进行对比，证明了本文的混合方法是一种可靠的预测远场噪声的全新方法。

1 数值方法

对于亚声速射流轴对称模态，扰动和射流剖面都是二维的，可以用二维柱坐标系下的Navier-Stokes方程进行直接数值模拟。基于Stromberg等[18]的实验数据分析，Sandham等[13]给出了二维基本流速度的表达式，并广泛运用于后续研究。本文也采取同样的基本流，对于任意流向x、径向r的点，其流向速度的表达式如下：

其中：

为了与边界条件匹配，需要加入小的并行流co-flow，流向速度进一步改写为：

为了和文献[12，14，18]的条件匹配，本文参数设置为：远场流速度与射流中心速度的比值uco-flow=1%，Ma =0.9，Re = 3600（特征长度为喷口直径D）。图1给出了5个不同位置的流向速度剖面图，可以看出，沿流向剪切厚度逐渐增加，直至完全发展。

图1 基本流速度剖面Fig.1 Velocity profiles of the mean flow

2 流场计算与分析

本文选取了文献[14]中的两种情况（表1中的A1、A2）进行计算。考虑对称性，计算域只取上半部分，为方便声场的计算，进行了扩大。最终的计算区域为：x方向从0到80D，r方向从0到50D。表1给出了不同情况的详细参数，其中ω1、ω2为加入的两个主波频率，差频 Δω=ω2-ω1，A0为初始幅值。

图2给出了A1、A2、B2的频谱图像（r/D=0.7，x/D=0、2、5、12），其中，红线和蓝线为本文计算结果，绿线为文献[14]的计算结果。从图中结果可以看出两者吻合程度很好。在x/D = 0处，两个主波（ω1、ω2）的幅值最大；在x/D = 2处，差频和谐波发展起来，此时主波还基本符合线性演化规律；到x/D= 5处，流动处于核心区末端，非线性作用增强，差频扰动的幅值达到了和主波相同的程度；继续演化到x/D=12处时，差频扰动幅值已经超越了主波，成为了主导。

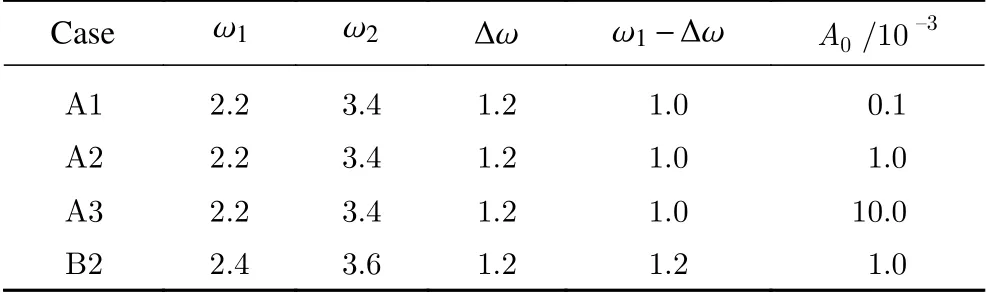
表1 入口扰动参数Table 1 Parametersof inlet disturbance waves

图2 压力波动的频谱Fig.2 Spectra of pressure fluctuations

A2和B2的演化过程相近，随着x位置的增加，差频扰动不断增强，直至超越主波。两者不同点在于：B2中初始主波分别对应差频的2～3倍频，因此频谱图上差频的倍频效应突出，频率为4.8和6.0的波也显著增长，此特征在x/D=12处体现得更加明显，这将对声源及远场声辐射产生巨大影响。

分析可知，随初始压力幅值增大，差频效应体现更加明显。为研究初始扰动幅值对扰动波非线性作用的影响，文中比较了A1、A2、A3三种情况的流场扰动压力的幅值曲线（图3）。

在A1中（图3（a）），非线性作用产生的差频扰动幅值较小，流场接近线性发展；增大初始幅值（图3（b）），差频压力幅值明显增大，在x/D = 7处达到最大值，超越主波，峰值达到主波峰值的一半，这表明非线性作用显著；当初始幅值为A0=1×10-2时（图3（c）），差频压力的峰值已经完全超越主波ω1，并且次差频扰动（ω1-Δω=1.0）的幅值迅速增长，二次非线性效应作用明显。

3 声源与声场分析

通过对亚声速自由剪切层的相干结构声辐射的研究，Zhang和Wu[8]指出，对于平板自由剪切流，可以将流场划分为主层、临界层以及远声场。当相干结构经过中性位置时，由于非线性作用和非平衡效应，扰动的速度在临界层的上下边界发生跳跃，而速度跳跃正是物理声源的主要来源，并由临界层内向外辐射声。用连续性方程将跳跃联系起来，便可求解得到声源项。对于轴对称射流情况，声源产生机理与平板自由剪切流相同，类似的方法可以给出等效声源，具体表达式如下：

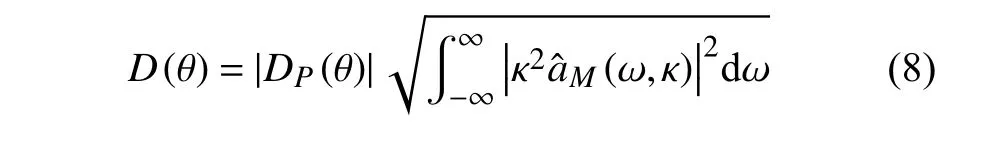
式（7）、式（8）便可用来计算远场声辐射强度和方向，其中，D(θ)为方位角函数，DP(θ)为 积分系数，为等效半径。具体推导过程和表达式参照文献[8]。

将时均声能换算成声压级SPL。图4给出了四种情况的SPL值分布，实线对应本文理论结果，虚线对应经验公式（9）。对比发现两种方法得到的声场非常接近。

图3 扰动压力的幅值曲线Fig.3 Amplitudesof fluctuating pressure

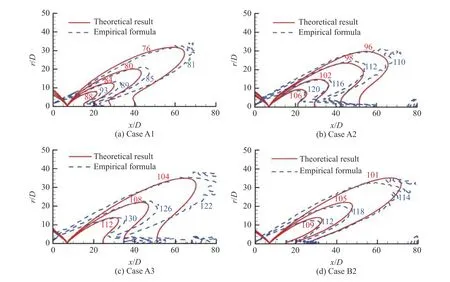
图4 四种情况的SPL等值线Fig.4 Contoursof sound pressure level for four cases

在A1中（图4（a）），声场与射流轴线夹角呈30°向远场辐射，有很强的方向性。这一现象和超声速马赫波辐射相似，表明不稳定波的线性演化会产生非紧致声源。即，声源尺度远大于声波波长，辐射强度集中，辐射角度较小。情况A2、A3中（图4（b）和图4（c）），贴近轴线处有出现微弱声强度值，原因在于非线性作用的增强使得声源频谱变宽，微弱紧致，紧致成分在30°以内辐射的声场强度变化不大。但即便存在紧致成分，整体辐射方向依然具有强方向性，与射流轴线夹角呈30°。对于B2，其声场表现出不同于上述三种情况的特点，与A2相比，两者幅值相同，但B2贴近轴线处的声强度很小，说明其声源非紧致更加显著。这种非紧致与A1的线性发展情况不同，是非线性和倍频共同作用的结果。两种方法计算得到的SPL值在大小上还有差异，但误差程度是符合预期的。

为详细分析导致声源紧致的因素，本文给出不同频率对应的声辐射强度大小。D(θ)是评估声辐射强度的重要参数，其代表时均声能随角度的变化。图5给出了四种情况中各个频率对应的D(θ)曲线。比较图5（a、b、c）可以看出，初始幅值增大，声辐射强度也随之增大，不同频率对整体声辐射的贡献呈现明显差异。图5（a）中，频率为ω1=2.2的主波声辐射占主导地位，其强度的峰值占比为93%，方向与轴线夹角呈30°。Δω=1.2的差频声辐射强度峰值只有主波ω1=2.2 的，次差频几乎为零。由此表明，不稳定波线性发展时，低频主波更易辐射声场，其声源非紧致，声场方向性明显，此时差频扰动和高频主波辐射强度较小，对总声场影响不大。当幅值提高到A0= 1×10-3时（图5（b）），差频扰动的声辐射显著增大，取代了ω1=2.2的主导地位，并且次差频的声辐射强度也增加到与主频ω1=2.2相同程度。差频和次差频产生的声源略微紧致，从而导致总声场在贴近轴线处有较大强度。当幅值再次提升至A0=1×10-2时（图5（c）），低频主波又“追赶”上来。四个波的声辐射强度相当，产生的总声场有明显方向性的同时也具备发散特点，其方向性来源于低频主波，发散来自于微弱紧致的差频和次差频声源。

图5 不同频率对应的声波方位角函数Fig. 5 The directivity of emitted sound waveswith different frequencies

对比图5（b）和图5（d）（分别对应情况A2和B2），两个主波的声源都非紧致，辐射成单瓣状结构，但对整体声辐射贡献较小，非线性作用产生的ω=1.2的频率波声强度最大，占主导地位。两种情况的差别在于，B2中贴近轴线方向辐射强度较小，产生的ω=1.2的频率波声源非紧致，而A2的差频波声源略微紧致。这说明频率相同的差频波也会产生不同的声源类型。此外，B2的方位角函数大小是A2的两倍，表明当次差频和差频两者的频率重合时，差频效应更为显著，会增大声辐射强度。

图5（a、b、d）中，高频主波的声辐射强度最小，根本原因在于不稳定波演化过程中，高频成分幅值变化快，进入中性点之前就衰减完全，因此对下游远场的声辐射几乎为零。而图5（c）中，由于入口扰动初始幅值很大，导致主波和差频波幅值变化处在同一水平，因此四个频率产生的声强度都接近。

4 结论

本文采用DNS方法对Ma=0.9、Re = 3600射流轴对称模态的线性及非线性的演化过程进行了分析，结合Wu理论模型分析，给出了等效声源项的表达式，计算了声辐射的强度和方向，分析了声源的影响因素，得到以下结论：

1）不稳定波的初始幅值影响流场的非线性演化，幅值增大，非线性作用增强，产生的声辐射也变大。

2）非线性作用产生的差频扰动在远场声辐射中的强度占比最大，非线性愈强，声源愈紧致，低角度下的辐射范围较宽，但有着明显的方向性，与射流轴线夹角呈大约30°向外辐射。

3）主频扰动和差频扰动还会通过非线性作用产生次差频扰动波，当差频和次差频扰动频率相同时，辐射强度显著增强，同时声源特性会发生改变，由紧致向非紧致靠拢。

本文准确计算了亚声速射流的远场声辐射的方向性和强度，与实验以及理论给出的结果非常吻合，可对亚声速射流噪声的预测提供一种准确且高效的混合方法。