三段翼型气动噪声特性数值分析
2023-01-05薛丝丹何嘉华刘秋洪蔡晋生
薛丝丹,何嘉华,刘秋洪,蔡晋生
(西北工业大学翼型叶栅空气动力学重点实验室,西安 710072)
0 引 言
气动噪声抑制已经成为大型客机亟待解决的一个关键技术问题。大型客机气动噪声主要是动力装置噪声和机体噪声[1]。其中,动力装置噪声主要来自风扇、压气机/涡轮、燃烧和喷流等,机体噪声主要来自增升装置和起落架。随着大涵道比涡轮风扇发动机、消声短舱、锯齿喷嘴技术的应用,动力装置噪声显著降低,在客机噪声中所占比例日益减小。动力装置在客机着陆时处于低功率状态,而增升装置和起落架处于开启状态,此时机体噪声已经接近甚至超过动力装置噪声。研究增升装置气动噪声对控制客机起飞、着陆噪声,提高客机市场竞争力都有极为重要的意义。
气动噪声数值预测方法已成为指导低噪声设计的重要工具。计算流体力学(computational fluid dynamics, CFD)和声比拟理论相结合的混合计算气动声学方法是工程应用中最受欢迎的气动噪声预测方法。其核心思想是首先采用数值方法求解N-S方程获得气动声源,然后利用自由空间格林函数求解声比拟方程[2]模拟声传播。混合计算气动声学方法对网格尺度和声学积分面的选择没有太多限制,在预测低马赫数流动诱发的气动噪声时可忽略四极子源项的贡献[3]。声场准确预测需要精细的声源信息。高雷诺数工程湍流的仿真可采用大涡模拟(large eddy simulation, LES)、分 离 涡 模 拟(detached-eddy simulation, DES)和雷诺平均模拟(Reynolds averaged Navier-Stokes, RANS)。LES[4]直接数值求解大尺度湍流,而对小尺度湍流则采用亚格子模型,由于在壁面附近需要精细的网格分辨率,因此计算成本高。RANS流动模拟成本低,但不能反映湍流的细节,无法准确预测流动分离。DES[5]对壁面附近的内层流动采用RANS模拟,而远离壁面的外层流动由LES求解,充分利用了LES和RANS的优点,是气动声学领域中最常用的声源模拟方法。DDES(delayed detached-eddy simulation)[6]方法可以避免边界层中RANS过早向LES切换。
李伟鹏[7]对大型客机增升装置气动噪声的产生机理与噪声控制技术进行了综述。客机的增升装置一般具有前缘缝翼和后缘襟翼,如30P30N翼型和L1T2翼型。众多学者采用实验测试手段[8-10]和数值预测方法[11-15]对这两种增升装置的气动特性和噪声特性进行了细致研究,结果均表明三段翼增升装置的气动噪声主要由低频窄带噪声、中频宽频噪声和高频窄带噪声组成,其中高频窄带噪声主要来自于缝翼尾缘涡脱落,低频噪声是缝翼剪切层Kelvin- Helmholtz不稳定性导致声波与剪切层之间形成反馈回路所产生[7,12],中频噪声的产生机理目前还没有明确的定论。其他三段翼构型的气动噪声是否也是主要由缝翼处的流动决定还需要进一步研究。
我国也将增升装置技术列入大型民机设计的重点突破领域,对客机增升装置开展了卓有成效的设计研究工作[15]。本文采用混合计算气动声学方法对某三段翼的气动噪声进行数值研究。气动声源模拟采用IDDES(improved delayed detached-eddy simulation)方法,噪声传播预估采用Curle方程[16]。数值算法利用圆柱-翼型绕流算例进行验证。
1 数值方法描述
1.1 气动声源数值模拟方法
采用有限差分法求解三维可压缩非定常N-S方程以获取精确气动声源信息。空间离散采用六阶优化格式[17],时间推进采用二阶隐式DDADI算法[18],湍流模型采用基于SA模型的DDES方法。
在SA一方程湍流模型基础上对DDES方法进行改进。在DES方法中,RANS和LES计算的切换依赖当地的长度尺度:
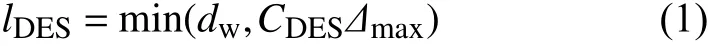
其中, Δmax=max(Δx,Δy,Δz),dw为网格单元与壁面之间的距离, CDES为常数。DDES方法构造一个屏蔽函数fd来避免边界层中RANS过早向LES切换:
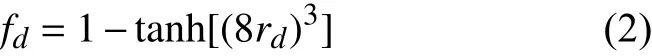
其中rd为无量纲参数。当地长度尺度重新定义为:

由于涡黏系数的过高估计,DES和DDES一般都会推迟剪切层中自然不稳定性的发展。我们采用下述长度尺度Δω替 换 Δmax:
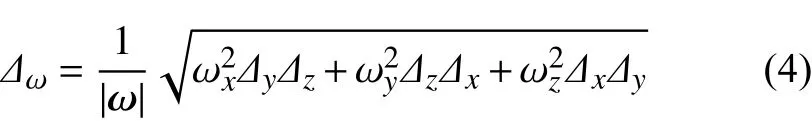
其中ωx、ωy和ωz代表当地涡量的单位分量。另一个改进是采用了如下近壁面函数分布律:
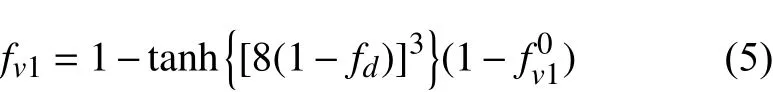

在远离壁面的LES区域,参数fv1、 fv2和fω固定为1.0、0和1.0。
1.2 气动噪声数值预测方法
对于低马赫数流动与固体边界相互作用诱发的气动噪声,可忽略四极子声源对远场的贡献。当固体边界静止且刚性时,Curle方程的积分形式在频域下可近似表示为[3]:

式中,p 和p′分别表示单位面积固体表面作用在流体上的力和声压, x(x1,x2,x3)和 y(y1,y2,y3)分别表示观察点和声源,φ是角频率,G(x,y,φ)为 格林函数,n为固体边界的外法线方向。噪声计算过程中选择固体表面S为积分边界。
假设声学介质均匀运动的速度为(u∞,0,0),声波传播速度为c0,格林函数G(x,y,φ)可写为:
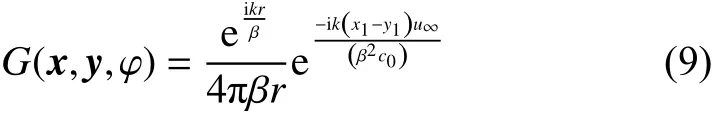
2 数值方法验证
对圆柱-NACA0012翼型绕流的气动噪声进行数值预测,通过与实验测试结果[19]对比,验证上述算法的可靠性。NACA0012翼型弦长C=100 mm,翼型上游100 mm处有一直径D=0.1C圆柱,实验段翼型和圆柱的展向长度均为L=3C 。无穷远来流迎角为0°,速度为u∞=72 m/s (对应的马赫数约为Ma=0.2)。基于圆柱直径和翼型弦长的雷诺数,分别为Red=4.8×104和R ec=4.8×105。
气动声源的数值模拟采用三维结构化网格,展向长度取实验长度的即0.3C。先生成二维网格,网格量约为16万(如图1所示),后沿展向拉伸45层得到三维网格,总网格量约为700万。
图2为瞬时展向涡量的分布云图,圆柱脱落的卡门涡街往下游移动,撞击到翼型前缘时涡结构产生严重变形与拉伸。翼型前缘区域有涡量较强的大尺度涡,周围还伴随有一些小尺度湍流涡。圆柱脱落的大尺度涡系结构运动到翼型的中部时已完全破裂,在翼型中部和后缘仅存在小尺度湍流涡。

图1 圆柱-翼型网格Fig.1 Configuration of Meshgird of rod-airfoil
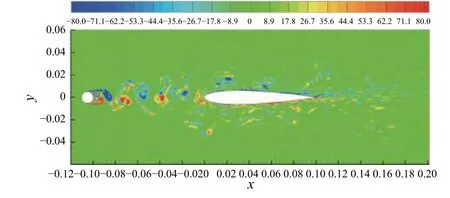
图2 圆柱-翼型瞬时展向涡结构Fig.2 Snapshotsof the instantaneous spanwise-vorticity structure of rod-airfoil
站位x/C=-1.04 和x/C=0.25处的时均速度型及其与实验值的对比如图3所示。数值模拟结果在x/C=-1.04站 位与实验吻合良好,在x/C=0.25站位的翼型表面附近则存在较小的差异。这主要是由于圆柱和NACA0012翼型均为对称模型,在实验测试中,圆柱和翼型的对称轴位置在y轴方向存在2 mm的偏差,而数值模拟没有考虑该偏差,导致圆柱尾涡脱落对翼型的冲击作用与实验状态存有一定差别。

图3 两个站位处的时均速度型Fig.3 Mean streamwise velocity profilesat two x-axispositions
图4为站位x/C=-1.04 和x/C=0.25处流向脉动速度均方根值与实验结果的对比。数值解与实验值基本一致,脉动在物面处最强烈,随着与物面间距离增加,脉动强度减小,距离增加到 x/C=0.4后,速度脉动几乎为0。

图4 流向脉动速度均方根值Fig.4 Root-mean-square valuesof the streamwise velocity fluctuation profile
为验证气动声源数值模拟的准确性,在翼型上表面选择一点,对该点的静压功率谱密度(PSD)进行分析。静压功率谱密度的大小通过如下定义衡量:
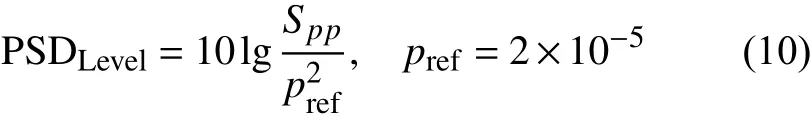
其中Spp是静压的单边功率谱密度。图5是数值计算结果与实验测试值的对比图,其中无量纲频率定义为St=。在St=0.2附近存在明显的峰值:数值计算得到St=0.193,对应的功率谱密度为115.95 dB/Hz;实验测试所得St=0.190,对应的功率谱密度为115.89 dB/Hz。St 的计算相对误差约为2.1%。在St=0.6附近也存在一个较小的峰值,数值计算得到的无量纲频率和功率谱密度与实验值非常接近。
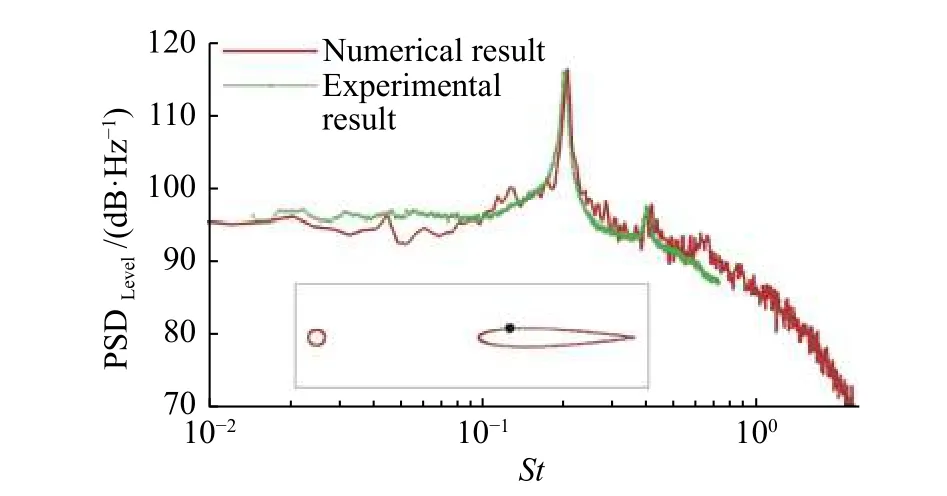
图5 翼型表面压力功率谱密度Fig.5 Power spectral density of surface pressure on airfoil
气动声源模拟中采用的展向长度为0.3C,而噪声测试的展向长度为3C,因此在声学远场的计算过程中将声源数据沿展向复制10份。选取远场观测点坐标为(0.5C,18.5C,1.5C),图6为观测点噪声功率谱密度与实验值的对比。数值预测的噪声功率谱密度与实验结果吻合,最高峰值91.3 dB/Hz出现在St=0.198处,而实验所得噪声最高峰值91.8 dB/Hz出现在St=0.195处 。以点(0.5C,0.0,1.5C)为 圆心、半径为18.5C圆上布置180个观察点,数值解取频率St=0.198,实验值取频率St=0.195,声压功率谱密度的指向性分布如图7所示,数值解与实验值趋于一致。

图6 观测点噪声功率谱密度预测结果Fig.6 PSD prediction result at a selected observer
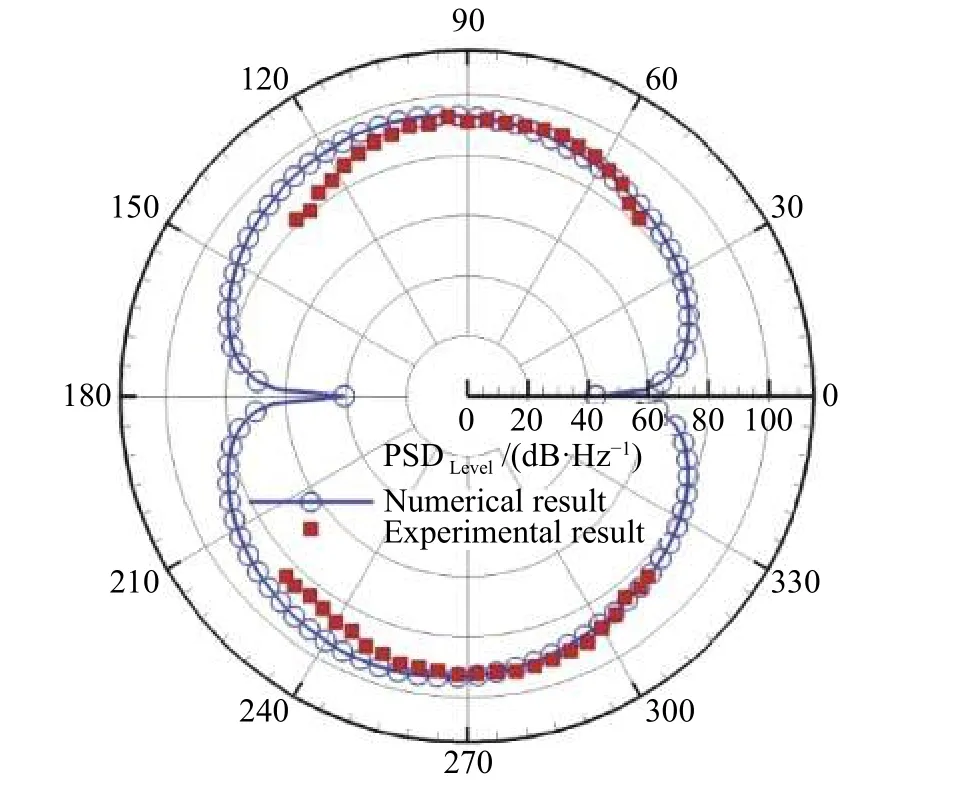
图7 声压功率谱密度指向性图Fig.7 Directivity of sound pressure power spectral density
3 三段翼气动噪声特性数值分析
3.1 三段翼模型与网格
高升力三段翼构型如图8所示,其参考长度为缝翼和襟翼闭合时的翼型弦长457.0 mm。缝翼偏角39.4o,长度为62.6 mm,是参考长度的13.7%;襟翼偏角15.7o,长度为152.8 mm,是参考长度的33.4%。无穷远来流参数为:马赫数0.17,温度295.56 K,迎角7.5°,基于参考长度的雷诺数 Re=1.71×106。
先生成二维网格,网格量约为37万,第一层网格高度为1×1 0-3mm,在缝翼和襟翼处进行网格加密(如图8所示),保证三段翼表面各处满足y+<1。沿展向拉伸50.8 mm,并布置45层网格单元,总网格量约为1660万。

图8 高升力三段翼型网格Fig.8 Illustration of Meshgrid of three-element high-lift airfoil
3.2 时均流动结果
流动计算时间步长为Δt=5.8×10-6s ,流动计算收敛后,选取9280个时间步的流动数据进行时均流动参数统计。图9为三段翼表面时均压力系数分布图,清晰地展示了前缘缝翼和后缘襟翼对升力的贡献。与30P30N翼型升力系数相比,本文三段翼的缝翼上表面吸力峰值较高,而主翼前缘上表面的吸力峰值偏低。

图9 三段翼表面时均压力系数分布Fig. 9 Time-averaged pressure distribution on the airfoil surface
三段翼附近时均速度的分布如图10所示,在前缘缝翼凹腔和主翼尾部凹槽的回流区内存在明显的低速区,同时襟翼尾缘区域由于边界层流动的分离出现低速区,而高速区主要集中在缝翼和主翼前缘的背风区。
湍动能(turbulence kinetic energy,TKE)在一定程度上反应了湍流脉动的强弱,由于其表达式与Lighthill声比拟方程右端气动源项中的应力张量项近似,常被用为评估远场噪声的一个指标。图11给出了时均二维湍动能分布,其定义如下:
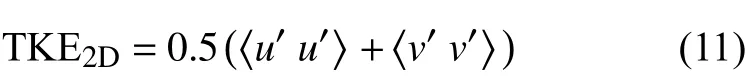
湍动能的分布主要位于缝翼和主翼回流区,以及襟翼流动分离、尾迹区。此外,由于缝翼和主翼后缘尾迹的影响,分别在主翼和襟翼前缘的上表面出现了高湍动能区域。

图10 三段翼时均速度分布Fig.10 Time-averaged velocity contour around the airfoil
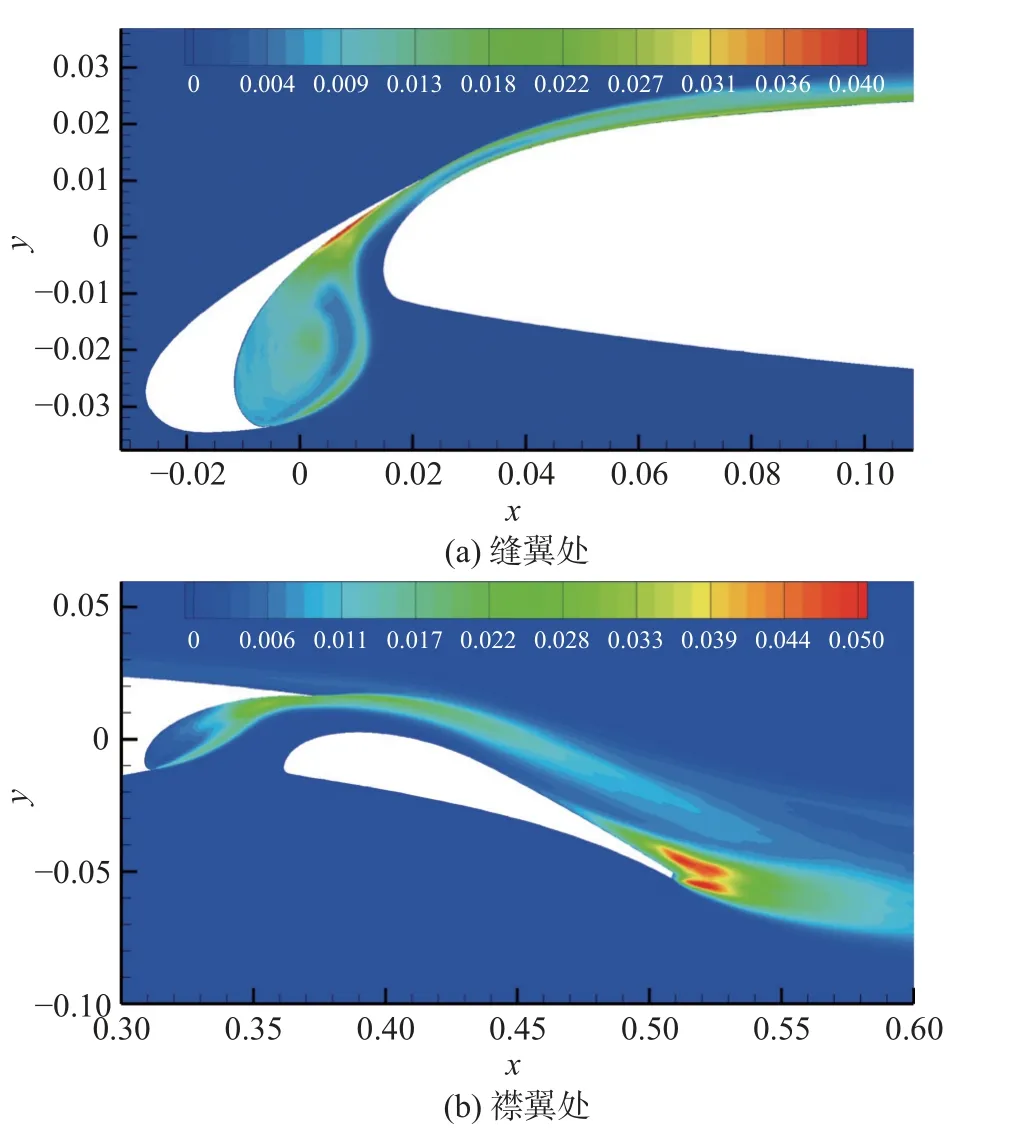
图11 二维湍动能分布Fig. 11 Resolved 2Dturbulent kinetic energy contours
3.3 瞬时流动结果
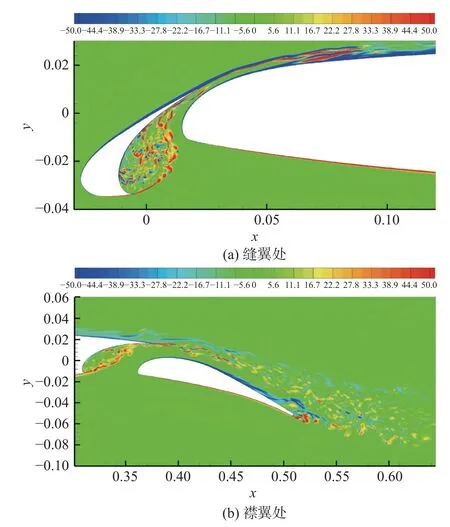
图12瞬时展向涡量云图Fig.12 Contours of instantaneous spanwise vorticity
图12 为瞬时展向涡量在缝翼和襟翼附近的分布云图。气流经过缝翼前缘时在尖点处发生分离,在缝翼凹腔内形成自由剪切层,剪切层经过发展会在下游再附于缝翼靠近尾缘的下表面,在再附区与缝翼下表面之间形成一回流区。在涡的撞击、融合和分离等因素的共同作用下,回流区内包含不同尺度和强度的涡结构。因剪切层外部流动的影响,流动从再附区到尾缘处发生了强烈变形和扭曲。缝翼尾缘脱落的涡随高速气流运动,与缝道内流出的涡融合后撞击在主翼前缘表面。襟翼的流动特征与缝翼相似,在尾缘发生流动分离,伴随着涡的生成、混合、撞击和脱落等复杂现象。
翼型表面不同位置处的静压功率谱密度如图13所示。缝翼凹腔前缘形成的剪切层流动在PS2点附近再附着,导致PS2点功率谱密度高。缝翼尾缘脱落涡含较强高频(14500 Hz附近)能量,经发展后撞击在主翼PM1点区域,使得该区域压力也含强高频分量。流动经过主翼PM2点附近时发生分离,在凹槽内形成自由剪切层,最后再附着于主翼尾缘下表面PM3点区域。PM2点形成的剪切层含强烈的高频成分,在回流区内经过分离和融合后,高频分量的能量被削弱。流动在襟翼尾缘PF1点附近发生分离,其高频分量的能量比PM2点低。
3.4 气动噪声特性分析
翼型声学模型展向长度为50.8 mm,在声学计算过程中将声源数据延展向复制,合计展向长度为1524 mm。气动噪声预测将三段翼固体表面作为积分面。在展向对称面上均匀布置360个观察点,半径为十倍弦长。其中三个观察点角度分别为135°、270°和290°,如图14所示。湍流数值模拟过程中共输出24150个时间步数据,将这些声源数据平均分成七份,每两份数据组成一段,即每一段采用6900个时间步数据,后一段与前一段数据重叠率为50%。将每一段时域数据加Hanning窗后进行FFT变换,结果乘以恢复系数后即可得到频域声源信息,利用自由空间格林函数和频域声源信息进行积分预测远场声压。将六段声源数据得到的噪声结果利用pwelch算法计算功率谱密度。
将缝翼、主翼和襟翼表面压力脉动产生的噪声分别定义为缝翼噪声、主翼噪声和襟翼噪声。数值预测的噪声总声压级(OASPL)指向性分布如图15所示。缝翼对声场的贡献小,主翼居中,襟翼最大,这与三段翼30P30N的噪声特性存在明显的不一致。虽然缝翼与襟翼的噪声指向性不同,但均在垂直于各自偏角的方向上达到最大值。
图16为135°、270°和290°三个观察点处的噪声功率谱密度频谱。对135°观察点的声场,缝翼表面压力脉动的贡献最小,主翼表面压力脉动的贡献最大。噪声主要集中在3000 Hz内,最大噪声峰值出现在1075 Hz。而对于270°和290°观察点的声场,缝翼噪声贡献依旧最小,襟翼贡献最大,噪声最大峰值出现在825 Hz,同时在中频4500 Hz附近也出现了明显峰值。图17为825 Hz、1075 Hz和4500 Hz噪声功率谱密度指向性分布。可以看出,825 Hz和4500 Hz噪声主要来自于襟翼,而1075 Hz噪声则是襟翼噪声和主翼噪声的综合结果。

图13 不同位置处的压力脉动谱Fig.13 Spectra of pressure fluctuationsat various locations
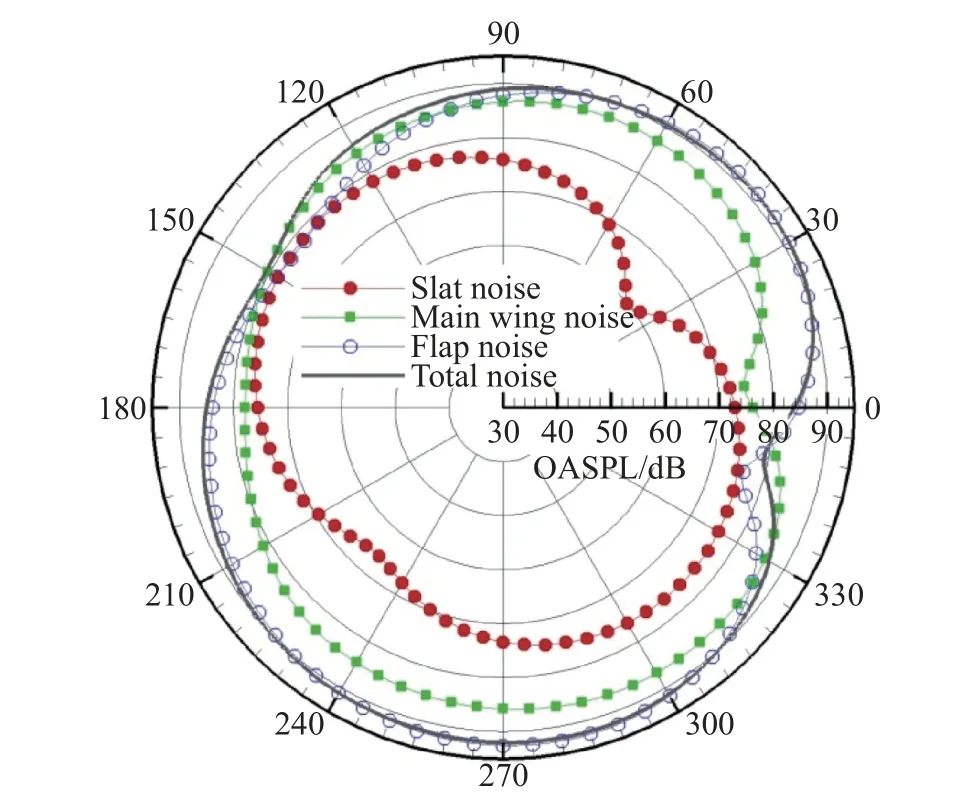
图15 声学远场指向性分布Fig.15 Acoustic directivitiesof the far-field

图14 观察点示意图Fig.14 Schematic of the observer locations
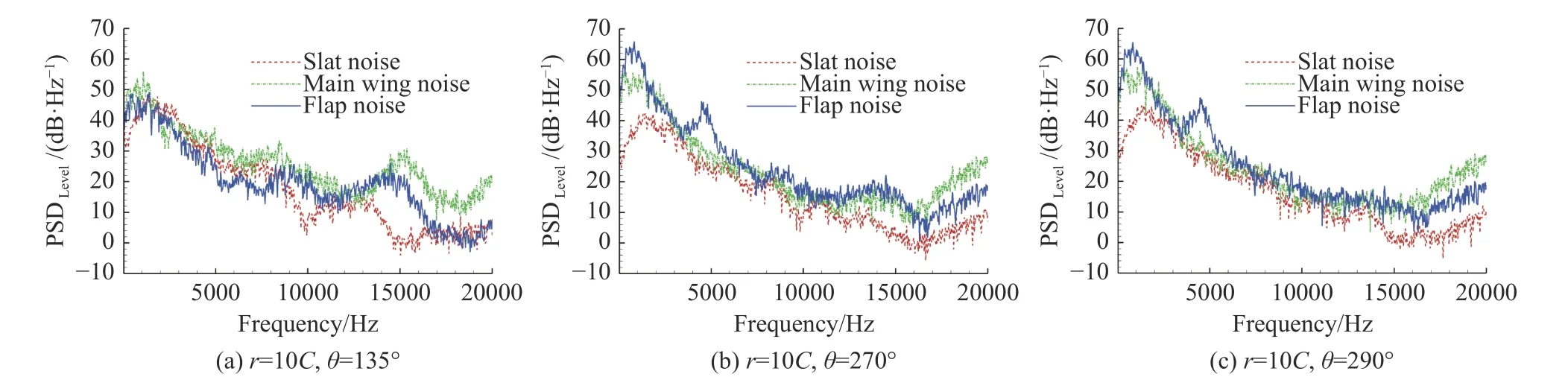
图16 三个观察点处的噪声预测结果Fig.16 Noise prediction resultsat threeobserver points
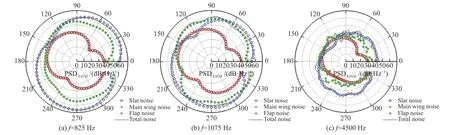
图17 不同频率噪声指向性分布Fig.17 Directivity distribution of noise at different frequencies

图18 流动DMD分析的子域Fig.18 Sub-zonesfor flow DMDanalysis
利用瞬时流场的脉动压力,开展流动动态模态分解(DMD)研究。根据图12,将产生涡结构的主要流动区域分解为如图18所示的A~E 5个子域。利用4096个时间步的脉动压力数据对这5个子域进行DMD分解。DMD方法可直接获得单频的动态模态所对应的流场,不需再使用其他频谱分析方法获取模态的频率。
图19为5个子域的DMD模态频谱图。子域D和E的流动主特征模态是位于500 Hz以下的低频,也就是说缝翼凹腔与尾缘处的流动分离主要产生500 Hz以下的低频噪声。子域A流动主特征模态频率836 Hz和1060 Hz,与观察点噪声频率825 Hz和1075 Hz相对应。子域C也存在与噪声频率825 Hz和1075 Hz相 对 应 的 流 动 特 征 模 态 频 率817 Hz和1056 Hz,但能量要小很多。子域A的4410 Hz和子域C的4691 Hz流 动 特 征 模态 频 率 对 应于4500 Hz附近的噪声频率。子域B流动主特征模态频率为10183 Hz。
DMD模态是对非定常流动中大尺度涡结构的动态分解,体现了某频率下大尺度涡结构的空间分布特征。提取子域A中836 Hz、1060 Hz与4410 Hz对应的流动模态和子域C中817 Hz、1056 Hz与4691 Hz流场振荡模态,以及子域E流动的109 Hz、274 Hz和1379 Hz模态,分别如图20、图21和图22所示。
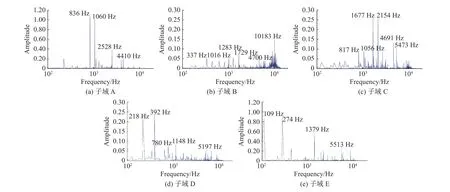
图19 子域DMD模态频谱Fig.19 DMDmode spectrum of sub-zones
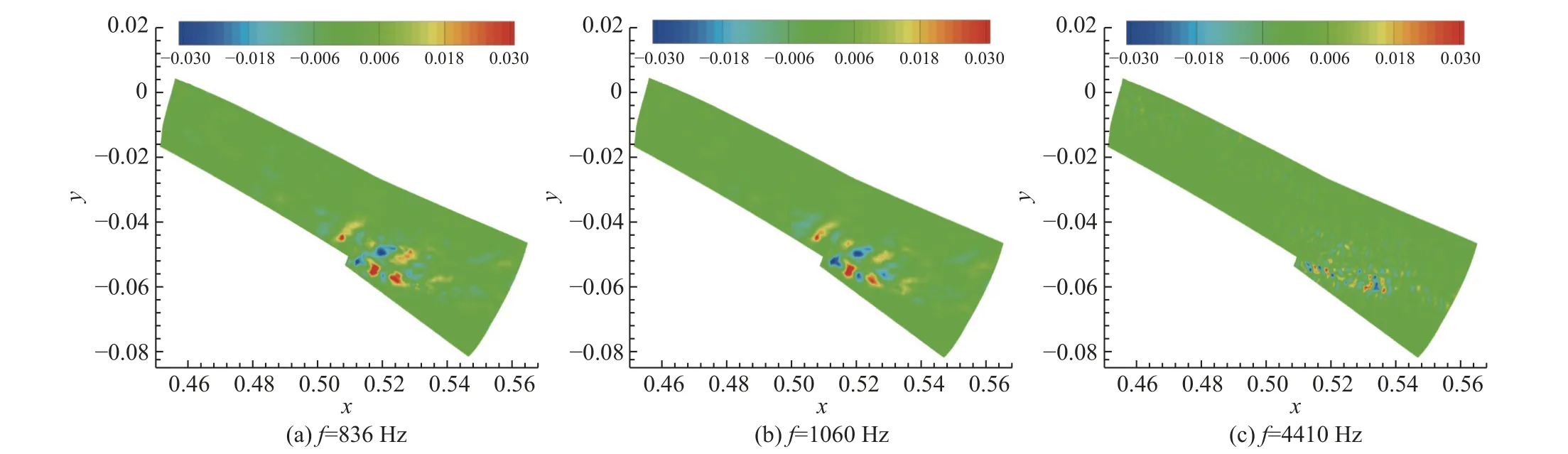
图20 子域A中836 Hz、1 060 Hz与4 410 Hz对应的DMD模态Fig.20 DMD modes corresponding to 836 Hz, 1 060 Hz and 4 410 Hz in sub-zone A
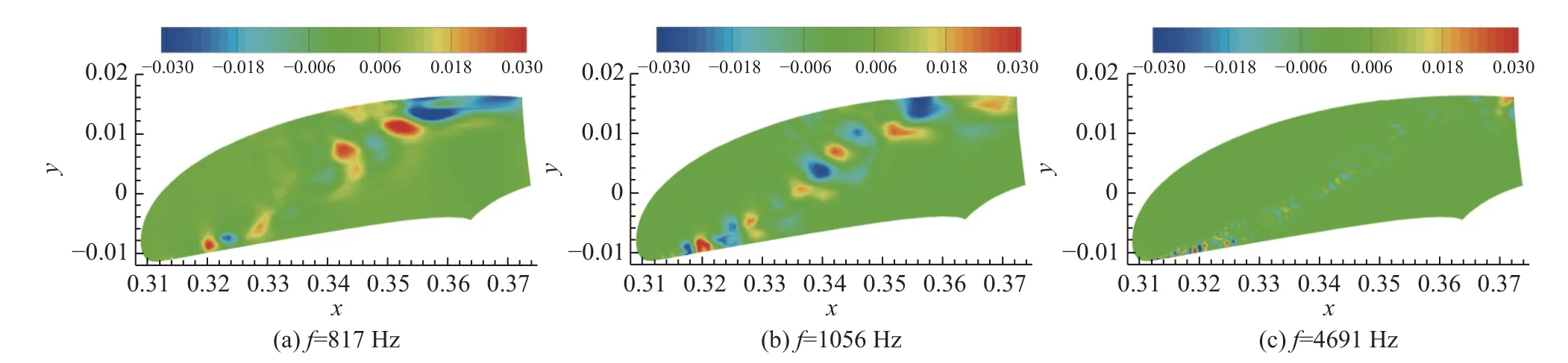
图21 子域C中817 Hz、1 056 Hz与4 691 Hz对应的DMD模态Fig.21 DMD modes corresponding to 817 Hz, 1 056 Hz and 4 691 Hz in sub-zone C
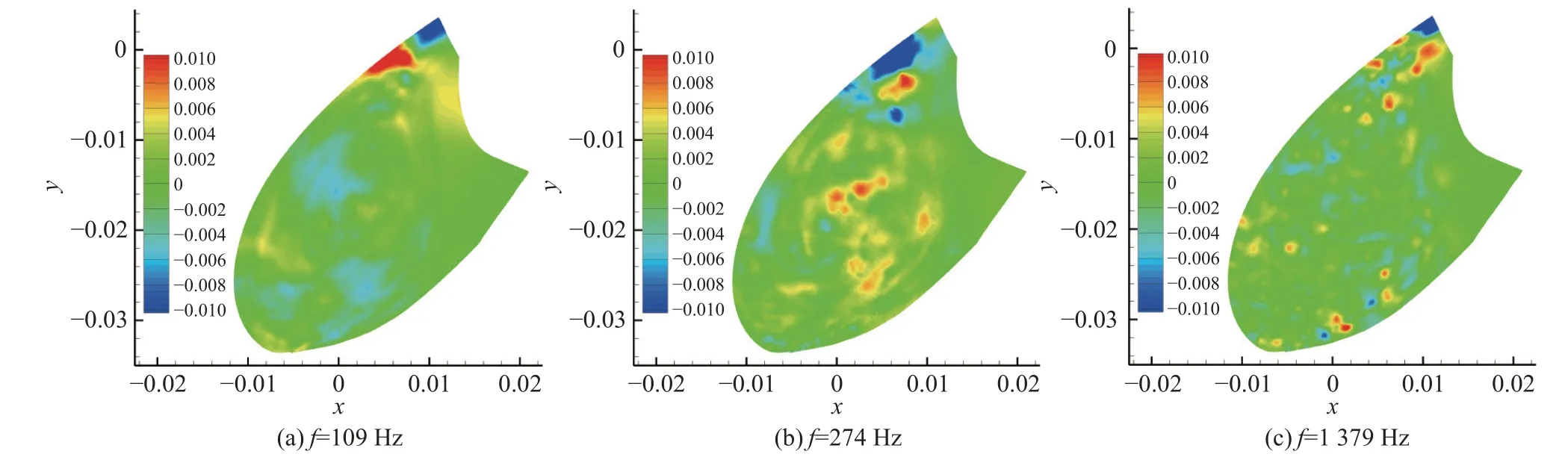
图22 子域E中109 Hz、274 Hz与1 379 Hz对应的DMD模态Fig.22 DMD modes corresponding to 109 Hz, 274 Hz and 1 379 Hz in sub-zone E
对于子域A的流动,襟翼尾缘的剪切层流动分离和尾涡脱落以及两者间的混合产生了836 Hz和1060 Hz的振荡模态,4410 Hz的流动模态则由襟翼尾涡脱落引起。气流经过主翼后缘下方时在尖点处分离,使得子域C流动产生4691 Hz模态,脱落涡经融合发展后在下游再附于主翼靠近尾缘的下表面,从而形成817 Hz和1056 Hz的流动模态。类似于主翼后缘凹腔内的流动,气流在缝翼前缘尖点处发生分离而在缝道内形成涡脱落、融合和撞击,使得子域E诱发109 Hz、274 Hz和1379 Hz等低频流动模态。
4 结论
采用混合计算气动声学方法对某三段翼气动噪声特性进行数值分析,气动声源的模拟采用IDDES方法,噪声传播的预估采用Curle方程。对于圆柱-NACA0012翼型绕流气动噪声算例,不同站位的时均速度、流向脉动速度均方根值、翼型表面压力功率谱密度和观测点噪声功率谱密度数值预测结果与实验结果相吻合,验证了数值方法的可靠性。
三段翼气动噪声分析结果表明:DDES方法能精细捕捉翼型涡脱落、融合和撞击等非定常流动现象,可为远场气动噪声传播的预测提供足够精确的声源信息;与三段翼30P30N的气动噪声特性显著不同,该三段翼的襟翼表面脉动压力对远场噪声贡献最大,而缝翼表面脉动压力的贡献最小;最高峰值噪声出现在1000 Hz附近,主要由襟翼尾缘剪切层流动分离和尾涡脱落及其混合作用产生;缝翼凹腔内的涡脱落、融合和撞击等主要产生500 Hz以下的低频噪声;4500 Hz附近的中频噪声则因襟翼尾涡脱落和主翼后缘下方流动分离产生。
由于计算资源的限制,研究过程中没有对气动声源模拟的网格无关性进行研究,亦没有考虑四极子声源对远场的贡献。在后续研究中,我们将采用更精细的网格对近场声源和远场噪声进行更精确地预测,进而细致分析三段翼气动噪声的产生机理。
