一种气动大差异性数据多任务学习方法

张 骏，张广博，程艳青，胡力卫，向 渝，汪文勇

(1.电子科技大学，成都 611731；2.中国空气动力研究与发展中心，绵阳 621000)

0 引言

传统预测气动特性的方法采用的计算流体力学（computational fluid dynamics,CFD），模型是已知的，由一组偏微分方程定义[1]。例如，Suhas和陶文铨等研究代数和微积分预测传热、传质过程的数值计算[2-3]；张涵信等研究与物理分析相结合的计算流体力学[4]。随后发展出了基于代理模型的气动特性预测方法。如：乔建领等研究了广义Burgers方程和声爆传播射线的计算方法[5]；许晨舟等研究了基于RANS方程的非结构网络求解器TNS的气动特性计算[6]；韩忠华等研究了基于代理模型的气动优化设计[7]。这些都取得了很好的研究成果。然而，偏微分方程的求解需要花费大量的计算资源和时间成本，一些高阶复杂的偏微分方程还可能不存在数值解[8-9]。近年来，深度学习作为一种数据驱动的方法，开始用于解决复杂的高维、多尺度和非线性问题，其建模的速度和模型预测的精度都有所保障。因此，基于深度学习的空气动力学建模方法近年来备受关注[9-14]。较有代表性的研究包括：何磊和钱炜祺等研究了机器学习方法在气动建模中的应用[15]，并使用长短时记忆神经网络进行非定常气动力的预测[16]；陈海等使用卷积神经网络预测翼型的法向力系数[17]。

基于深度学习的空气动力学建模方法通常采用全连接神经网络（FCN）和卷积神经网络（CNN）。Muller等使用FCN方法建立了描述湍流近壁动力学的低阶模型[18]；Yilmaz等使用CNN方法建立了根据翼型形状预测飞行性能的模型[19]；Zhang等使用CNN预测翼型升力系数[1]。上述研究创造性强，取得了较大成果，但这些研究都没有考虑建模数据之间的差异性。而深度学习作为一种数据驱动方法，训练集数据是影响模型精度的关键因素之一，当训练集数据存在较大差异性时，会对模型预测结果产生较大影响[10]。在气动应用中，翼型的外形参数和飞行状态参数在数据类型上存在较大差异，如果同时使用这两种参数进行气动性能预测，二者会对预测结果产生不同量级的影响；如果忽视这种差异，不合理的参数空间则会造成预测结果精度的损失。因此，如何同时关联状态参数和外形特征参数进行气动特性预测，是深度学习领域预测气动特性的一个问题。深度学习领域多任务学习法（multi-task learning,MTL）的出现为解决此问题提供了一种新思路[20]。

多任务学习的思想是将整个学习网络划分为多个功能网络来训练数据的不同区域。当训练数据集输入到学习网络中时，会将数据集划分为多个“任务”。在进行训练的时候，每个任务只会激活其对应的功能网络，只针对该任务进行相关知识的学习，随后对所有学习到的任务知识进行融合得到输出结果。相比较于传统深度学习网络中，同一个网络对所有的训练数据进行学习的方式，多任务学习网络的每个功能网络在处理其对应的任务时都能够更“专一”地提取该任务的相关知识，因此特别适用于大差异性数据建模的场景。相较于传统神经网络结构，其预测精度更高。多任务学习已经应用于机器学习的许多领域，从自然语言处理[21]和语音识别[22]到计算机视觉[23]均取得了成功。

本文主要研究翼型的外形数据和飞行状态参数对飞行器升力系数和阻力系数预测结果的影响。本文的主要创新之处在于：由于外形参数和状态参数类型差异性较大，本文将多任务学习与集群网络[24]相结合，将气动外形参数和飞行状态参数的学习划分为不同任务，并分别输入到对应的网络学习，最后将所有集群的输出进行融合得到最终的预测结果，该方法能提高建模预测的精度，并分析这些数据之间的差异性对预测结果的影响。

1 研究基础

1.1 数据差异性

研究已经证明，深度学习建模的预测精度受到多种因素的影响，其中训练集的数据集质量是影响预测精度的关键因素之一，而数据集中样本的分布、样本的种类也都是影响数据集质量的重要因素[10]。Hu等[20]研究了训练集样本分布不均所带来的训练集质量差对深度学习建模的影响，并且提出使用多任务学习的方法来提高样本分布不均时的模型预测精度。但是文献中样本数据的分布不均体现为不同数据之间的大小差别，未考虑数据类型本身的差异。

训练集样本数据的类型差异性同样是影响模型预测精度的重要因素。Dakua等研究了样本数据的类型差异性对模型预测精度的影响，使用24种不同类型的数据进行建模，证明不同类型的数据对预测结果的影响程度不同[25]。如果需要同时联合两种或多种类型的大差异性数据进行建模，则不同数据类型的数据会对预测结果产生不同程度的影响，而传统的深度学习网络模型忽视了这些差异性的影响，进而造成模型预测结果精度的损失。

1.2 多任务学习网络和集群网络

机器学习领域的传统多任务学习方法有两种，一种是硬参数共享方法，另一种是软参数共享方法[21]。硬参数共享方法在任务划分之前设定共享隐层，随后划分任务，使每个划分好的任务同时学习，同时保留各个任务对应的输出层。软参数共享方法则是首先划分好任务，使得每一个任务都有自己的模型和自己的参数，不同模型所对应参数之间的差异使用正则化进行约束，最后保留各个任务对应的输出层。

这两种多任务学习方法虽然在诸多领域取得了成功，但是面对诸如翼型的外形参数和飞行状态参数这两种截然不同的数据时，要提前获知这两种数据之间的差异性对预测结果的影响比较困难，而集群网络的出现则使分析数据之间的差异性成为了可能。

集群网络的起源最早可以追溯到自然语言处理领域的混合专家模型[20,26]。它的思想是，根据输入数据的标签激活一个特定的专家网络，最后对所有专家网络的结果进行融合，得到最终结果。2019年发展出了以集群网络为形式的部分神经元激活模型[24]。集群神经网络具有许多个集群，每一个集群都会识别出数据集中对应的数据区域进行学习。每一个集群又由功能网络和上下文网络组成，其中，功能网络负责与最终输出进行拟合，上下文网络负责给功能网络的拟合结果添加权重，即该集群对应的任务对于网络最终输出的影响系数，随后将二者进行融合得到该集群的输出结果。最后对每一个集群的结果进行再次融合得到最终结果。

与传统的多任务学习相比，集群网络能够通过上下文网络学习不同功能网络的相关知识对预测结果的影响系数，所以使用集群网络进行预测时，预测结果的误差要更小。White等在2020年提出了利用集群网络预测气流速度的方法，与传统深度学习模型相比取得了更小的预测误差和更快的训练速度[24]。

本文将多任务方法和集群网络相结合，提出了大差异性多任务学习网络（large-discrepancy multi-task learning network,LD-MTL）。该模型的详细结构在2.1节作出说明。

2 大差异性多任务学习网络LD-MTL

2.1 模型结构

本文所提出的模型结构如图1所示。该模型由任务划分和多任务学习两大模块组成。其中，任务划分模块将大差异性数据划分为外形参数和飞行状态参数两个子集，多任务学习模块由两个功能网络和一个上下文网络组成。

任务划分模块将输入数据划分为翼型参数和飞行状态参数两个子任务。其中，外形参数输入到功能网络1（Function network 1）进行学习，飞行状态参数输入到功能网络2（Function network 2）进行学习。同时，采用交替训练的方法将原始大差异性数据输入到上下文网络学习各个功能网络的权重，得到各个功能网络所学习到的相关知识对最终输出的影响程度。

图1 LD-MTL结构图Fig. 1 Structure diagram of LD-MTL

基于卷积神经网络（CNN）的空气动力学神经网络建模已经在图像处理、目标检测等领域取得了显著成果[1,13]，因此功能网络1采用CNN处理翼型外形参数。而全连接神经网络（FCN）是深度学习领域最基础最常用的模型，其灵活性强，模型的预测精度理论上可以通过增加隐层数或神经元数量进行提升，基于FCN的空气动力学神经网络建模同样也有显著的成果[11-12]，因此功能网络2选用全连接网络处理飞行状态参数。上下文网络同样选用全连接网络训练出各个功能网络对最终预测结果的影响程度。

2.2 模型描述及算法

2.2.1 任务划分模块

任务划分模块将输入的两类大差异性参数划分为两个子任务，分别对应深度神经网络部分的两个功能网络的输入，如式（1）～式（3）所示。本文所采用的数据中，两类大差异性参数分别为翼型外形参数（坐标参数）和飞行状态参数（攻角、马赫数）。

其中，R表 示模型输入的全部数据，N表示其样本数，r 表示两类参数的总数；P表示其划分的子任务1，即只含翼型外形参数的全部样本，p表示其参数个数；Q表示其划分的子任务2，即只含飞行状态参数的全部样本，q表示其参数个数。如图2所示。

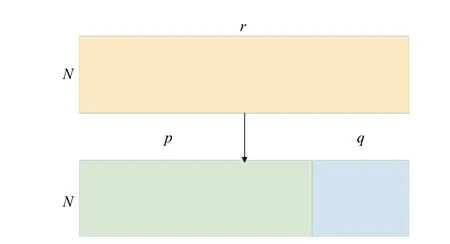
图2 数据划分示意图Fig.2 Schematic of the task allocation

2.2.2 多任务学习模块

如前所述，将子任务1“某一具体翼型外形参数”输入到功能网络1进行训练，拟合输出值阻力系数（CD）和升力系数（CL），将子任务2“该翼型飞行状态参数”输入到全连接神经网络进行学习。即式（4）、式（5）所示：

其中，m为 功能网络1的输出节点序号；f1m表示功能网络1的第m个输出节点的输出值，即根据外形数据拟合出的相关知识；fCNN表示功能网络1使用卷积神经网络；K 表示fCNN的输出节点个数；n为功能网络2的输出节点序号；f2n表 示功能网络2的第n个输出节点的输出值，即根据飞行状态参数拟合出的相关知识；fFCN表示功能网络2使用全连接神经网络；L表示fFCN的输出节点个数。

将两类大差异性数据R 输入到上下文网络进行学习，学习各个功能网络所学习的相关知识对最终结果的影响程度，如式（6）所示：

其中，cz表示上下文网络的第 z个输出节点的输出值，c fFCN表示上下文网络使用全连接网络。

对于给定的一个输入样本向量，LD-MTL的输出如式（7）所示：

其中：→y 表示整个网络的最终输出，即（CD,CL）；cm表示上下文网络为功能网络1分配的权重，即外形参数对最终输出的影响程度；cK+n表示上下文网络为功能网络2分配的权重，即飞行状态参数对最终输出的影响程度。由此可见，上下文网络的输出结果可以在一定程度上反映外形参数和飞行状态参数这两种大差异性数据之间的差异性。

模型的训练方法采用功能网络和上下文网络交替训练的方法，即：两个功能网络同时训练，功能网络和上下文网络交替训练。详细训练方法如下：

1）前向传播。前向传播的算法如式（1）～式（4）所述，损失函数如式（8）所示：

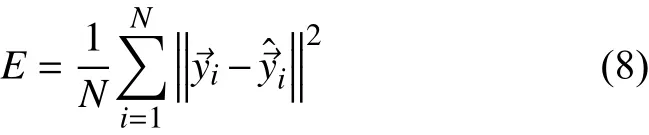
2）固定上下文网络，训练两个功能网络。功能网络的参数更新如式（9）所示：

其中，η为学习率，θf表示功能网络的神经网络参数，功能网络1和功能网络2都用式（9）进行参数更新。

3）固定两个功能网络，训练上下文网络。参数更新如式（10）所示：

其中，θc表示上下文网络的神经网络参数。

4）交替执行步骤1）至3），直至损失函数E收敛。

3 结果分析

3.1 数据集

本实验采用的数据集来自于公开数据库UIUC Airfoil Data Site[27]，数 据集具体内容 为CAST10-2翼型在马赫数为0.1～0.65、攻角为-0.5°～5°时升力系数和阻力系数的2352条样本数据，样本集的数据集格式如表1所示。第1至第562列表示翼型的外形坐标，X轴坐标和Y轴坐标交替排列。第563列是马赫数，第564列是攻角，第565列是阻力系数，第566列是升力系数。

对数据集的预处理有如下步骤：

1）对数据进行Min-Max归一化处理。即：

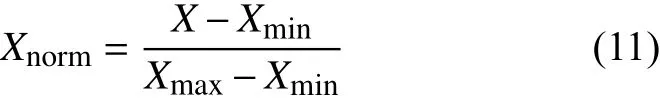
其中，Xnorm表示归一化后得到的值，X为数据原始值，Xmin表示此数据的最小值，Xmax表示此数据的最大值。

2）将数据集按照8∶1∶1的比例划分出训练集、验证集和测试集。训练集用作深度神经模型的训练，验证集用于模型训练过程中对预测结果精度的参考，测试集用于模型最终的精度评估。

表1 数据集格式Table 1 Format of the dataset

3.2 实验结果分析

本文设计了具有不同超参数的LD-MTL，并将结果与全连接神经网络和卷积神经网络进行比较。所有神经网络都是用同样的训练集、验证集和测试集，网络的迭代次数都被设置为2000次，批处理大小设置为512，学习率设置为0.0003，最终预测结果的评估采用均方误差（MSE）和平均绝对误差（MAE），所有的网络训练都基于Python Pytorch1.8.1版本，英伟达RTX2060显卡。

3.2.1 CAST10-2实验结果分析

CAST10-2的实验结果如表2所示，表中第一列表示实验采用的方法，第二列表示其采用的网络结构，其中functionNet1表示功能网络1的结构，functionNet2表示功能网络2的结构，contextNet表示上下文网络的结构。fCNN(n,0/1)表示采用的卷积神经网络CNN具有n个卷积层，0/1表示不带有/带有池化层。FCN(a,b,c,d)表示采用的全连接神经网络从输入层到输出层各层的神经元数量分别为a、b、c和d。例如fFCN(2,5,5,2)表示一个四层全连接神经网络，它各个层数的神经元数量分别为2,5,5,2。MSE(CD)表示测试集中CD预测值的均方误差；MSE(CL)表示测试集中CL预测值的均方误差；MAE(CD)表示测试集中CD预测值的平均绝对误差；MAE(CL)表示测试集中CL预测值的平均绝对误差。

表2 CAST10-2实验结果分析Table 2 Experiment result analysis of the CAST10-2 dataset

从表2中可以看到当功能网络1设置为2个卷积层且带有池化层时，对CL和CD的预测误差最低，因此本文采用LD-MTL_3作为LD-MTL最优结构。从表2中还可以看到，不同参数的LD-MTL预测误差均优于采用纯CNN的结构，这说明传统的CNN网络从翼型外形参数和飞行状态参数这两种大差异性数据中学习到气动特性的相关知识并融合这些相关知识进行气动特性预测的能力比LD-MTL差。其中LD-MTL_5采用了与其他LD-MTL结构不同排列顺序的翼型坐标输入数据，结果表明LD-MTL结构对CL和CD的预测精度并不会受到输入数据中翼型坐标数据的不同排列影响。原因是LD-MTL在翼型数据输入到功能网络1之前对数据进行预处理，使得CNN中每一次卷积操作都分别只针对X坐标和Y坐标，所以无论输入翼型数据排列方式如何，输入到功能网络1中的翼型数据排列方式都一样，如图3所示。而上下文网络是一个FCN，FCN每一层的每一个神经元都与下一层的每一个神经元相连接，因此XY坐标参数的顺序不同可以看作输入神经元的排列顺序不同，而这并不会影响全连接网络的输出结果。由于XY坐标参数的位置不同并不会影响LD-MTL的预测结果，同时Python神经网络计算过程存在许多随机数操作，所以实验结果均采用10次实验的平均值。

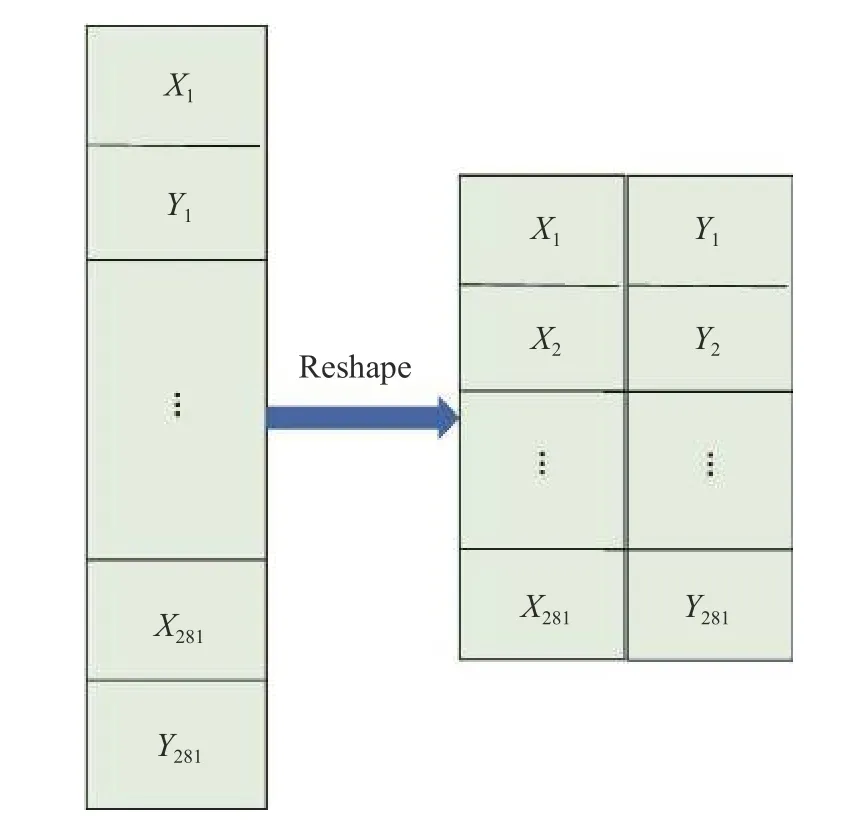
图3数据预处理示意图Fig.3 Schematic of the data preprocessing

图4 所示为表2中LD-MTL_3、LD-MTL_5、LDMTL_CL、LD-MYL_CD、CNN以及FCN_2这几个模型在验证集上的均方根误差变化曲线。

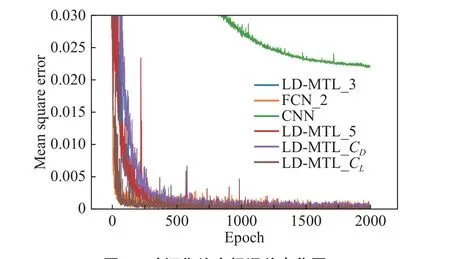
图4 验证集均方根误差变化图Fig.4 Mean square error variation for the validation datasets

分析图4可知，FCN_2和LD-MTL_CL的收敛速度最快，约在训练250轮时收敛；其次是LD-MTL_3及LD-MTL_5，约在训练500轮时收敛；LD-MTL_CD的收敛速度慢于前两者，约在训练1000轮时收敛；而CNN的收敛速度最慢，在完成训练2000轮时，CNN依旧没有收敛，且其在验证集上的损失明显大于其他结构的损失。同时LD-MTL_3和LD-MTL_5的损失曲线变化基本一致，这也说明了输入数据不同的坐标排列并不会对模型的训练产生影响。

表2中的LD-MTL_CD和LD-MTL_CL是使用与LD-MTL_3相同的结构分别单独预测CD和CL。根据实验结果得知，分别预测CD和CL时，模型预测对应气动力系数的精度比同时预测CD和CL低。分析图5所示的验证集损失函数变化图以及表2的测试结果，可以看到LD-MTL_CL的收敛速度大于LDMTL_3、大于LD-MTL_CD，且验证集上LD-MTL_CL的损失函数值小于LD-MTL_3，但最终测试集的结果却大于LD-MTL_3。验证集上的损失函数值是对模型性能的参考，而测试集上的损失则是对模型的最终评估，这说明LD-MTL_CL模型的泛化能力不如LDMTL_3，因此导致了LD-MTL_CL最终测试集的误差比LD-MTL_3大。而LD-MTL_CD无论在验证集上的误差、测试集上的误差还是收敛速度均逊色于LDMTL_3。

图5 损失函数变化图Fig.5 Lossfunction variation

同时对CD和CL进行预测时，训练过程中的反向传播过程传递给神经元的信息会同时包含CD和CL的相关知识，随后神经元再根据此相关知识进行节点权重的调节。而在单独预测CD和CL时，反向传播过程中传递的信息则只包含CD或CL的相关知识，所以造成了最终的预测精度不如同时预测。

表3为各个模型的训练时间和预测时间对比表，其中Time_t为训练时间，Time_p为预测时间。可以看出LD-MTL_3的训练时间和预测时间相较于CNN分别长了约24%及52%，但是MSE(CD)、MAE(CD)、MSE(CL)及MAE(CL)四项指标分别下降了约97.9%、87%、99.6%及95.4%；LD-MTL_3相较于FCN_2的训练时间长了11.3%，但是预测时间缩短了5.3%，四项评测指标分别下降了约11.4%、38.4%、54.2%及45.9%。分析可知，LD-MTL在与CNN和FCN对比时，能通过少量的训练时间的增加换取精度的大量增加，可见LD-MTL在进行大差异性气动数据建模时更具有优越性。

表3 CAST10-2实验结果耗时对比Table 3 Time consumption comparison for the CAST10-2 experiment

图6和图7展示了LD-MTL_3与传统CNN模型在预测CD及CL的精度差异。其中，每一个点的横坐标表示测试集中的真实值，纵坐标表示预测值，真实值与预测值越接近，点的位置越接近对角线。红色的原点表示使用CNN结构的每一个样本点，绿色的倒三角表示使用LD-MTL_3的相同样本点。可以看出，LD-MTL_3的样本点紧靠对角线附近；而CNN模型的样本点离对角线很远，拟合效果差。

图6 CNN和LD-MTL_3预测CD对比Fig.6 Drag coefficient comparison predicted by CNN and LD-MTL_3

图7 CNN和LD-MTL_3预测CL对比Fig.7 Lift coefficient comparison predicted by CNN and LD-MTL_3

图8 和图9展示了LD-MTL_3与FCN模型在预测CD和CL方面的差异。

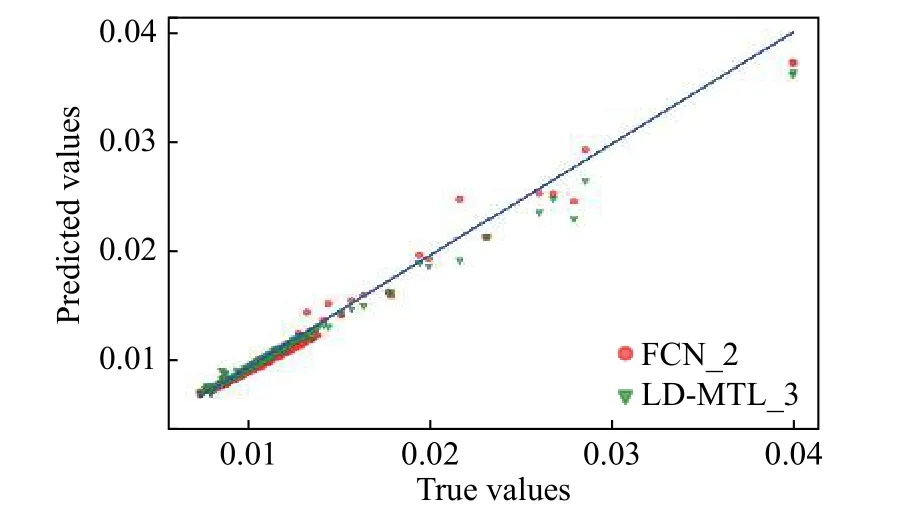
图8 FCN_2和LD-MTL_3预测CD对比Fig.8 Drag coefficient comparison predicted by FCN_2 and LD-MTL_3

图9 FCN_2和LD-MTL_3预测CL对比Fig.9 Lift coefficient comparison predicted by FCN_2 and LD-MTL_3

红色点表示FCN_2样本点的预测情况，可以看到LD-MTL_3在预测CD时，在小数值区域即CD＜0.02的区域拟合效果要比FCN好，而在预测CL时，LD-MTL_3的拟合效果在整个测试集样本空间都比FCN好。

在LD-MTL_3中，上下文网络的输出值可以视为外形参数和飞行状态参数的权重值。

随机选取如图10所示的CAST10-2翼型，筛选出此翼型外形坐标以及飞行状态差距在测试集中的样本点，将其训练出的权重值可视化，得到图11和图12所示的权重值图。图11和图12的横轴表示经过筛选后的样本点；纵轴表示权重的具体数值；红色柱体表示翼型的外形参数，上面的具体数字表示外形参数对最终预测结果的影响程度；蓝色柱体表示飞行状态参数。上面的具体数字表示飞行状态参数对最终预测结果的影响程度。可以看到在预测CD时，筛选出的五个样本点的红色柱体均要高于蓝色柱体，这说明当攻角处于-0.5°～5°的区间内的时候，对CD进行预测时，外形参数对预测CD的影响程度比飞行状态参数约大30%；而在预测CL时，筛选出的五个柱体的蓝色柱体均要高于红色柱体，这说明在对CL进行预测时，飞行状态参数对预测CL的影响程度比外形参数约大10%。

图10 CAST10-2翼型图像Fig. 10 CAST10-2 airfoil profile

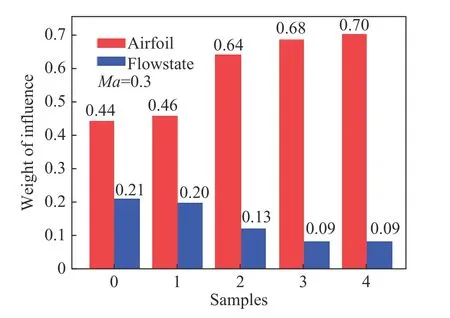
图11 预测CD时飞行状态参数和外形参数的权重图Fig.11 Weightsof the flow stateand airfoil for CD prediction

图12 预测CL时飞行状态参数和飞行参数的权重图Fig.12 Weights of the flow state and airfoil for CL prediction

通过上述结果及其分析可知，LD-MTL_3对于升力系数CL和阻力系数CD预测的误差比传统FCN小，且LD-MTL能够反映大差异性数据在建模时重要性的量化分析，而这是传统方法无法做到的。这些差异性量化分析将会在飞行器的设计和优化领域起到重要的参考作用。

4 结论

为了解决大差异性数据对深度神经网络建模预测精度产生较大影响的问题，本文提出了一种气动大差异性数据多任务学习方法。该方法将多任务学习方法与集群网络相结合，将不同的气动数据划分为不同的任务输入到对应的功能网络进行学习，最终融合输出预测结果。通过对CAST10-2翼型的大差异性融合数据建模实验，证明了在预测阻力系数和升力系数时，本文所提出的LD-MTL预测精度要高于传统的CNN网络和FCN网络；针对传统神经网络对大差异性数据的解释性不足的问题，LD-MTL能够量化分析大差异性数据之间的差异性，具有一定的可解释性。这对于实际的设计和开发具有重要的参考价值，值得进一步研究。

由于本文所采用的是处于低马赫数、小攻角下的数据集，考虑到空气动力学数据大多是高速、高维且复杂的数据，所以未来的工作将聚焦于以下内容：

1）进一步研究不同的功能网络和上下文网络结构对模型的影响，进一步提高模型的精度，使模型在高马赫数、大攻角条件下对差异性的量化分析能符合实际情况。

2）由于神经网络学习过程中的参数调整具有不确定性，故将上下文网络的输出作为权重，这点可能与实际情况的误差较大。下一步将结合灵敏度分析，分析出数据集中实际的权重情况，再应用于深度神经网络的训练；并且还将研究大攻角高马赫数下的外形参数和飞行状态参数的重要性。这将进一步提高LD-MTL的精度以及可解释性。