基于集成动态结构分析的故障检测

郭 金 玉， 王 霞， 李 元

( 沈阳化工大学 信息工程学院， 辽宁 沈阳 110142 )

0 引 言

由于现代工业设备的复杂性不断增加，工业过程的各个子系统之间联系紧密，任何一个单元发生故障都会影响生产过程的稳定运行和最终的产品质量[1-2]。目前大量的过程数据已经可以实时访问，过程监控可以成功检测异常操作行为、提高故障检测精度和减少误报。通过利用历史过程数据，基于数据驱动的故障诊断方法[3]为监控过程系统的稳定运行提供了强大的工具。

近几年，以数据驱动为基础的统计过程监测方法被应用于各种工业过程领域[4-8]。其中多元统计过程控制(multivariate statistical process control，MSPC)是对过程数据进行降维处理。传统的降维方法有基于高斯分布假设的主元分析(principal component analysis，PCA)以及基于非高斯分布的独立元分析(independent component analysis，ICA)。Kresta等[9]关于非线性数据的降维处理证明了核主元分析(kernel principal component analysis，KPCA)的有效性。主元分析不可避免地存在局限性，因为PCA关于数据分布的假设不适用于实际的工业过程。基于这样的假设，PCA提取的变量符合高斯分布，而许多实际工业过程中PCA提取的变量很少符合高斯分布。为了弥补PCA的不足，Kano等[10]提出ICA算法并应用于非高斯过程的故障检测，其性能优于一些在高斯分布假设下的故障检测算法。随着过程监控设备的完善，大多数过程并非是单模态的，而是具有较强的时间相关性。为了打破传统建模的局限，Vanhatalo等[11]将动态主元分析(dynamic principal component analysis，DPCA)用于统计过程监控，充分证明了该算法能够有效提取过程数据的动态特征，从而实现较好的检测效果。Lee等[12]提出基于动态独立元分析(dynamic independent component analysis，DICA)的统计过程监控。该方法构造带有时滞变量的增广矩阵，建立ICA模型，其目的是从自相关和交叉相关变量中提取统计上独立的分量，捕捉主要的动态特征，在动态过程监控中达到较好的检测效果。张成等[13]致力于对微小故障的研究，针对非线性动态过程中的微小故障，提出基于加权统计特征KICA的故障检测与诊断方法。李元等[14]提出一种动态局部邻域主多项式分析的故障检测方法，该方法对复杂的工业过程中出现的多模态以及动态时序问题给出了有效解决方法。Said等[15]提出一种改进的动态优化核偏最小二乘法，该方法应用于监控时变动态系统，不仅能够最小化计算成本和时间，并且还能选择简化的核函数集。

为了提取数据的局部结构信息，Hu等[16]验证了局部保持投影(locality preserving projections，LPP)算法在故障检测中的有效性。LPP只利用给定数据集的邻域几何流形，并倾向于将数据点投影到一个小区域，因此投影到低维子空间的数据集的外部形状可能会被破坏。在此基础上，大多数研究人员开始致力于监控过程数据的局部和全局结构信息。Zhang等[17]提出一种用于故障检测的全局-局部结构分析(global-local structure analysis，GLSA)模型，能够获得较多的局部与全局结构信息，因此该模型在故障检测领域中具有一定的优势。Tong等[18]对多流形投影算法(multi-manifold projections，MMP)在故障检测中发挥的重要作用给出有力证明。郭金玉等[19]提出一种动态多流形投影算法(dynamic multi-manifold projections，DMMP)。该算法能提取过程数据的局部和全局结构信息，在动态过程监控中具有较强的优越性。

为了进一步提高所建立的监测模型的适用性和可靠性，需要对给定数据集的结构信息进行彻底的保留，而不是单方面的保留。针对传统动态多元统计分析方法不能同时考虑给定数据集的不同结构特征问题，本研究提出一种基于集成动态结构分析(ensemble dynamic structural analysis，EDSA)的故障检测算法。EDSA模型利用DPCA、动态局部保持投影(dynamic locality preserving projections，DLPP)和DMMP模型，通过贝叶斯推理将多个检测结果组合在一个集成统计量中。这是由模式识别领域中普遍采用的集成学习技术所推动的。集成学习技术最近也被应用于非高斯过程监测中[20]。与DPCA、DLPP和DMMP模型相比，所提出的EDSA模型考虑了全局结构、局部结构及其并行权衡，这意味着集成检测方法能够检测到这三种几何分布的异常变化，因此所提出的故障检测方法对故障的敏感性高于任何单一方法。

1 集成动态结构分析算法

针对工业过程中存在的动态特性，许多研究学者开始对动态过程监控进行研究[21-24]。将处理动态过程的方法运用到过程监控中，较好地获取动态结构信息，进一步改善过程监控的性能。但是鉴于大多数算法都是以无监督的方式训练的，提取潜在变量的任何方式都将为提高过程监控性能提供有用的信息。因此，为了提高DPCA、DLPP和DMMP三种算法应用于过程监控的可靠性和适用性，通过集成学习的思想，将它们组合成一个集成统计量。在离线建模阶段，三种算法分别构建不同的监测模型，并计算相应的监测统计量以及控制限。然后通过贝叶斯推理将每个监控模型的SPE和T2统计量分别进行组合成一个集成统计量。若集成统计量超过控制限则为故障数据，反之，为正常数据。

1.1 动态主元分析

DPCA将时滞移位方法运用到PCA算法中，把原始数据集X=[x1,x2,…,xi…xn]T，xi∈m，通过时滞移位方法生成增广矩阵在此基础上执行PCA算法。若时滞参数lag=l，通过公式(1)生成的增广矩阵为n×[m×(l+1)]：

(1)

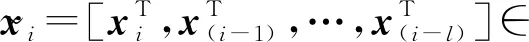
对增广矩阵进行标准化处理，通过PCA降维寻找一个投影p∈[m×(l+1)]×d，将转化到一个低维数据空间yi∈1×d。PCA目标函数为

(2)

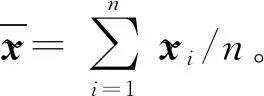
为了使得复杂的问题简单化，PCA算法将数据分解为主元矩阵和残差矩阵，转化为简单的求解特征值问题。原始动态矩阵分解形式如式(3)所示。

(3)

式中：P=[p1，p2，…，pd]∈m×(l+1)×d是由特征向量构成的负载矩阵，矩阵n×d也称为得分矩阵，E∈n×[m×(l+1)]为残差矩阵。

1.2 动态局部保持投影

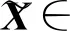
LPP算法的目标是找到一个投影轴p∈[m×(l+1)]×d，使原始数据点能够投影到新的坐标轴上，从而去除冗余数据，实现降维。在文献[25]中提出LPP的目标函数为

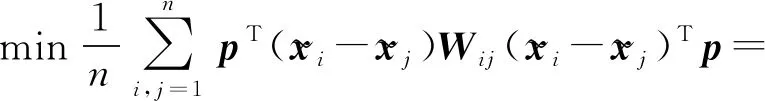
minpTL′p

(4)

式中：W为邻接矩阵。

(5)

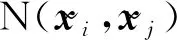
1.3 动态多流形投影算法

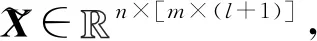
全局图最大值目标函数与PCA算法不同，目标函数为

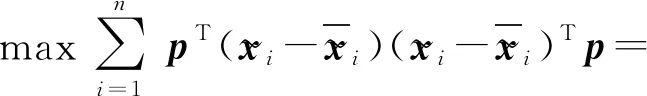
maxpTGp

(6)

(7)

通过优化两个目标函数获得一个统一的框架如式(8)所示。

(8)

式(8)通过简化转化为一个求解广义特征值问题。转化形式为

Gp=λL′p

(9)

假设p1,p2,…,pd是对应于式(9)的d个最大特征值λ1,λ2,…,λd对应的特征向量，捕获全局和局部信息的低维矩阵Y如式(10)所示。

(10)

式中：P=[p1,p2,…,pd]∈[m×(l+1)]×d为负载矩阵，Y=[y1,y2,…,yn]T∈n×d。

传统的检测方法都具有一定的局限性，而本研究提出的集成动态结构分析是一种将集成学习技术与现有故障检测算法结合的方法。每个监控模型都通过平方预测误差(squared prediction error，SPE)和T2统计量来检验模型的好坏。SPE和T2统计量的计算：

(11)

SPE=EET

(12)

(13)

三个监测模型分别通过公式(12)和(13)计算出各模型的统计量。

1.4 贝叶斯推理

利用Bayesian推理计算发生故障的概率[26]。

(14)

(15)

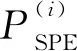
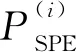
(16)

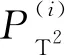
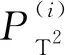
(17)

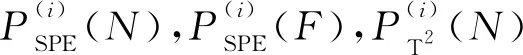
(18)

(19)

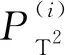
(20)

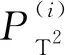
(21)

对每个模型的SPE和T2统计量的检测结果，利用Bayesian推理计算出故障产生的概率，将结果进行组合得到集成统计量：

(22)

(23)

2 基于集成动态结构分析的故障检测

运用集成动态结构分析算法进行故障检测时通常包括离线建模和在线检测两部分。离线建模主要是运用训练数据建立动态模型，计算统计量，并确定统计量的控制限；在线检测主要是运用集成统计量对测试数据进行在线检测，判断数据是否故障。

离线建模过程：

步骤1采集正常操作条件下的过程数据X=[x1,x2,…,xi,…,xn]T∈n×m，通过时滞移位方法生成包含动态特征的增广矩阵n×[m×(l+1)]，其中并对其进行标准化处理；

步骤3选取LPP的近邻参数，计算邻接矩阵W，求解局部最小值矩阵L′，求解广义特征值问题得到投影矩阵P，并计算SPE和T2统计量，建立DLPP模型；

步骤4构造MMP的目标函数，求解广义特征值问题得到投影矩阵P，并计算SPE和T2统计量，建立DMMP模型；

步骤5通过核密度估计方法计算每个模型的SPE和T2统计量的控制限。

在线检测过程：

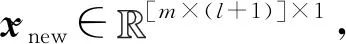
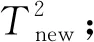
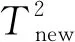
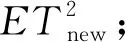
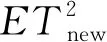
3 仿真结果与分析

3.1 数值例子

运用文献[27]中的动态过程的数值例子来验证方法的有效性，具体模型：

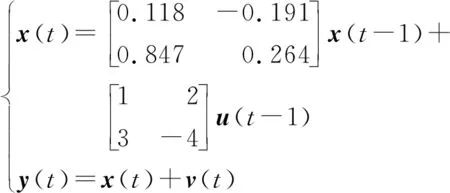
(24)

式中：v=[v1v2]T为随机噪声，均值为[0 0]T，方差为[0.120.22]T；u是一个与过程数据相关的输入且满足：

(25)

式中：w=[w1w2]T为随机噪声，均值为[0

0]T，

方差为[1 1]T。设置u(0)=[0 0]T，x(0)=[1 1]T。随机生成两组数据，分别是500个样本的训练数据和960个样本的测试数据，用来验证EDSA的有效性。从第161个样本起，w1的均值由0变化到4，并一直持续到过程结束。

为了验证本算法的有效性，将本算法与传统的DPCA、DLPP、DMMP和DICA算法进行对比。各种算法的参数设置：在DPCA、DLPP、DMMP、DICA和EDSA算法中，时滞参数l=2。根据85%的累计方差贡献率选择5种算法的主元或独立元个数：在DPCA算法中，选择3个主元；在DLPP算法中，选择4个主元；在DMMP算法中，选择1个主元；在DICA算法中，选择8个独立元；在EDSA算法中，选择8个主元。为了公平比较，所有方法使用核密度估计确定99%的控制限。因为DMMP算法选取了1个主元，所以无法用图形呈现样本的分布情况。DPCA、DLPP和EDSA算法在前3个主元空间上的样本分布以及DICA在独立元空间上的样本分布如图1所示。从图1(a)中能够明显看出，训练数据和故障数据都集中在控制限的内部，从而说明DPCA 算法无法在主元空间中检测故障数据，因此该算法的SPE和T2两个统计量的检测效果都较差。图1(b)呈现的效果与图1(a)类似，仅有极少量的故障数据在控制限外部，从而证明DLPP算法的检测率较低。图1(c)中故障数据大多数集中在控制限的内部，有少量故障数据分布在控制限以外，说明DICA算法在独立元空间中对故障数据的检测效果有所提高，优于DPCA和DLPP算法，但是检测效果仍不理想。从图1(d)中可以明显看出，大部分的故障数据在控制限外部，说明EDSA算法能够更好地捕捉数据中的动态变化，从而提高了对故障数据的检测性能，但是少量训练数据也出现在控制限外部，说明EDSA算法有较小的误报率。与其他3种算法相比，EDSA算法的检测效果最好，验证了该算法的有效性。

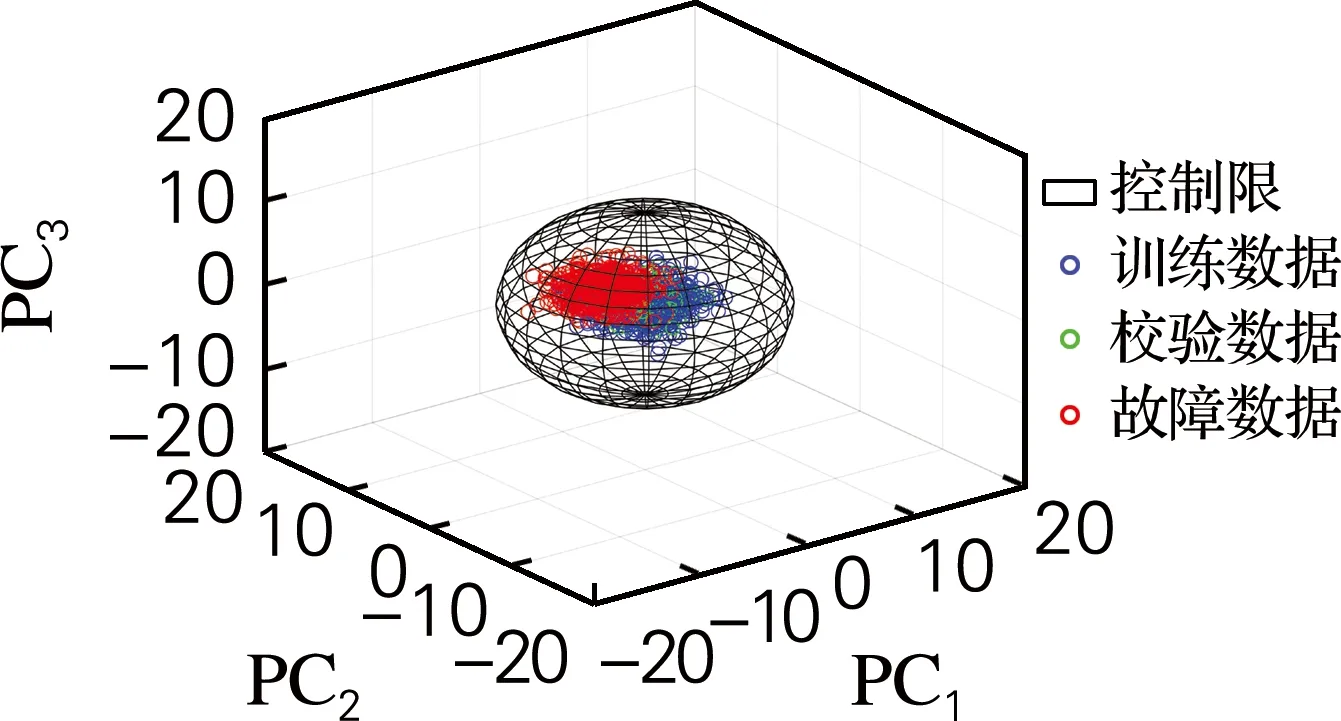
(a) DPCA

DPCA、DLPP、DMMP、DICA和EDSA方法的检测效果如图2所示，各种方法的故障检测率如表1所示。从图2可以看出，DPCA的SPE统计量无法对具有时间相关性的过程数据获取异常变化时的有效信息，因此导致极低的故障检测率，仅为0.13%；然而DPCA的T2统计量可以提取动态过程异常情况下的部分数据信息，相比较而言，检测率有所提高。但DPCA算法的检测率较低，这是因为残差空间中的数据对比主元空间具有极强的自相关性，所以DPCA的检测效果很差。相比DPCA，DLPP算法的两个统计量都能够捕捉到动态特征，但是检测率仍不理想。这是因为DLPP算法仅提取局部信息，忽略了全局信息。DMMP算法的T2统计量对动态过程的变化有较好的识别，检测率高达61.15%，而SPE统计量的检测率相比DPCA、DLPP也有提高。

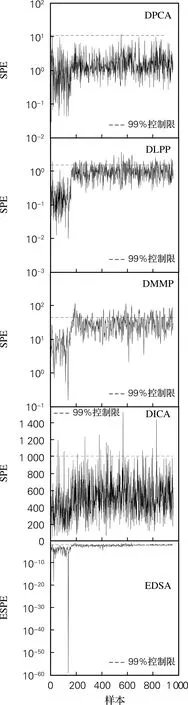
(a) SPE与ESPE

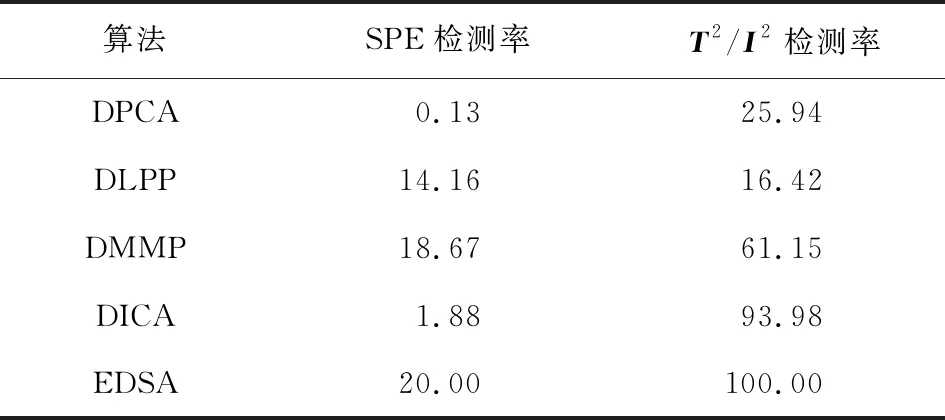
表1 各种算法对数值例子的故障检测率

DICA的SPE统计量几乎无法识别故障，测试数据中绝大部分的故障数据在控制限以下，检测效果不理想，I2统计量的检测效果好于DPCA、DLPP和DMMP算法。这是因为DICA算法在独立元空间中可以捕捉到过程数据的动态非高斯特征，从而能够提高检测效果。然而EDSA算法的2个监控统计量对过程数据都具有较好的监控能力，检测效果优于其他4种算法，其中T2统计量的故障检测率高达100%，检测效果最好。因为该算法将3种算法集成在一起，考虑了全局结构、局部结构及其并行权衡，可以有效地提取数据的自相关信息，从而达到较高的检测水平。

3.2 TE过程

田纳西-伊斯曼(Tennessee-Eastman，TE)过程由于其相对现实和复杂的特性，如今已经成为国际上通用的测试各种过程监控方法的标准仿真模型[28-30]。图3是由Lyman等[31]提出的TE过程工艺流程图。通过TE过程中常见的阶跃、随机和未知类型的3类故障进行仿真测试，其中选取的6种故障的描述如表2所示。

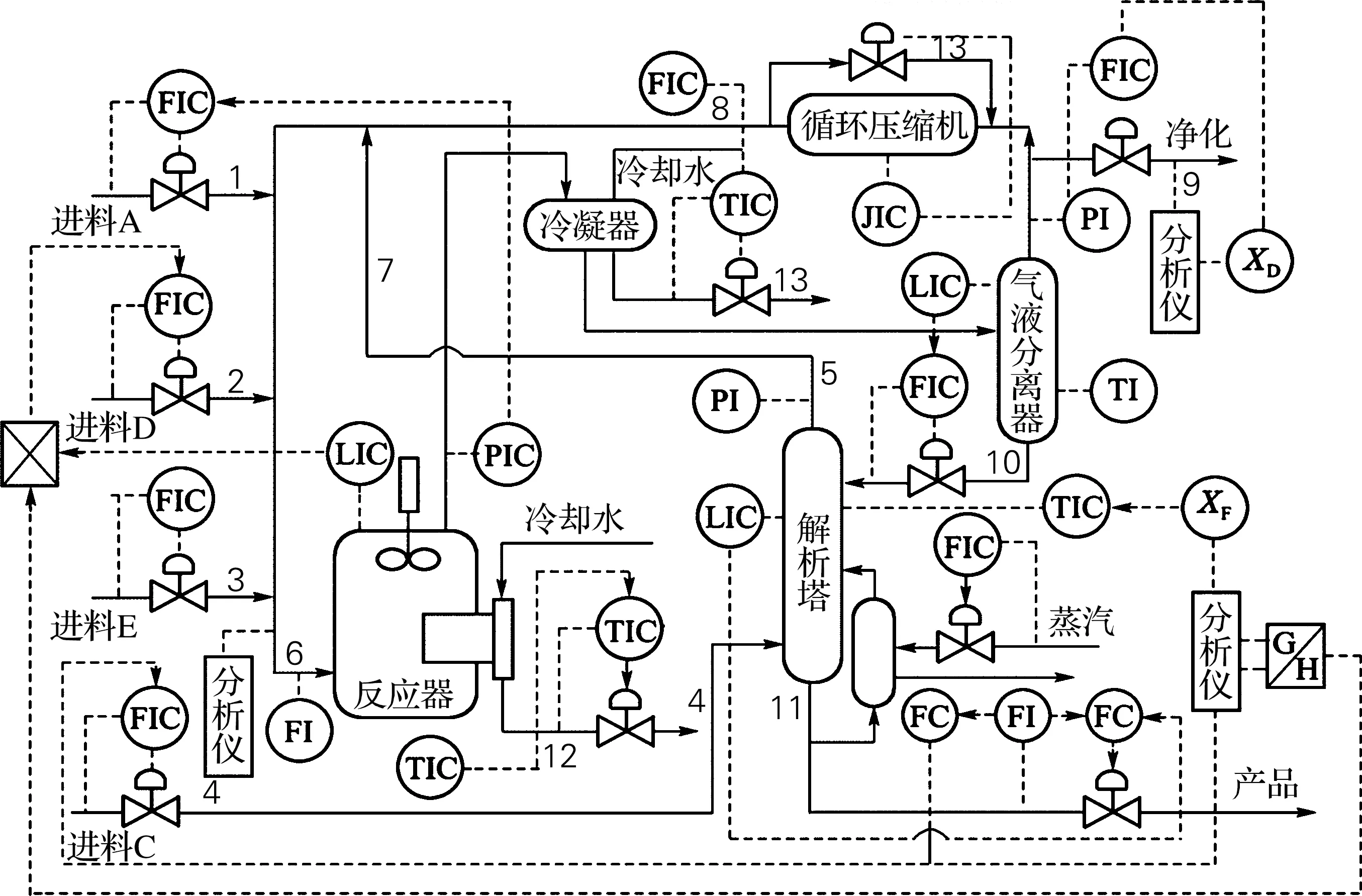
图3 TE过程工艺流程图

表2 TE过程故障类型

DPCA、DLPP、DMMP、DICA以及EDSA算法对故障4的检测结果如图4所示。从图中可以明显看出5种算法的各个统计量都具有一定数量的误报。对比之下，EDSA算法的误报率比其他4种算法略低一些。DPCA和DMMP算法的T2统计量对动态过程十分不敏感，发生异常变化时无法获取有效信息，从而导致故障数据都分布在控制限之下，检测率很低。这是因为两种算法在特征提取时，主元空间中的数据具有较强的自相关性，从而故障检测效果未能达到理想状态。DICA算法两种统计量的检测效果较低，无论在残差空间还是独立元空间都很难捕捉过程数据微小的动态变化，所以在检测故障4时呈现出较差的检测效果。在EDSA算法的T2统计量的检测图中，大部分故障数据都在控制限以上，检测率高达90.73%。对比5种算法的SPE统计量的检测效果，其中DPCA和EDSA具有明显优势，其检测率都能够达到100%。由此可知，EDSA算法具有较强的综合检测性能，其检测结果明显好于其他4种算法。这是因为EDSA将DPCA、DLPP与DMMP算法集成在一起，同时获取了局部和全局结构的信息以确保数据结构的完整性，从而达到较好的检测效果。将故障检测率作为对比指标来验证本文算法的优越性，表3是5种算法的故障检测率对比。从表3可以清楚地看出，EDSA与DPCA、DLPP、DMMP和DICA 4种算法的故障检测率对比，EDSA算法对大多数故障都具较高的检测能力，从而证明了EDSA算法在故障检测时的优势。

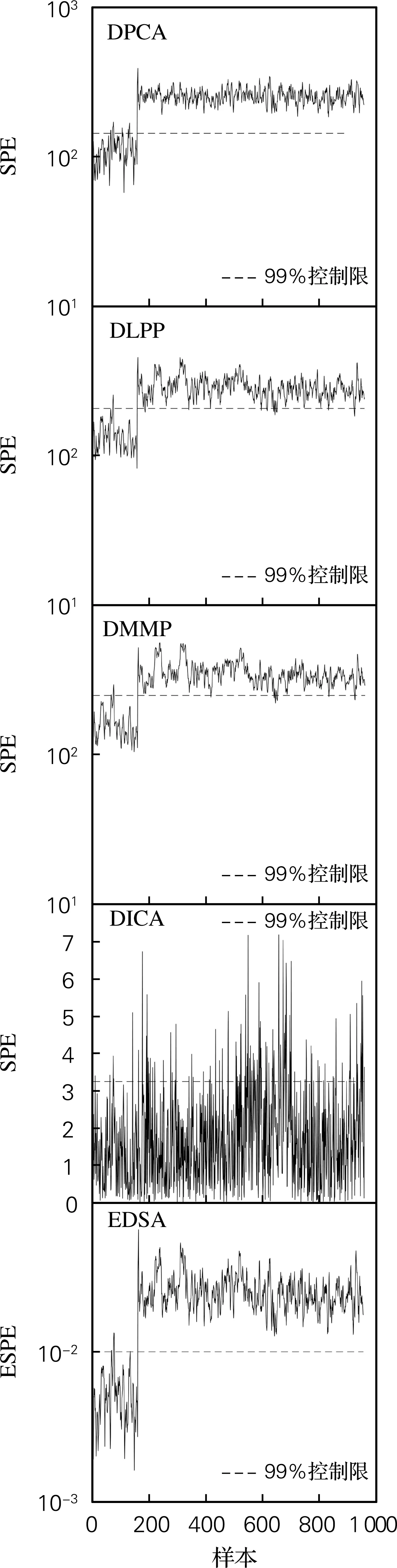
(a) SPE和ESPE

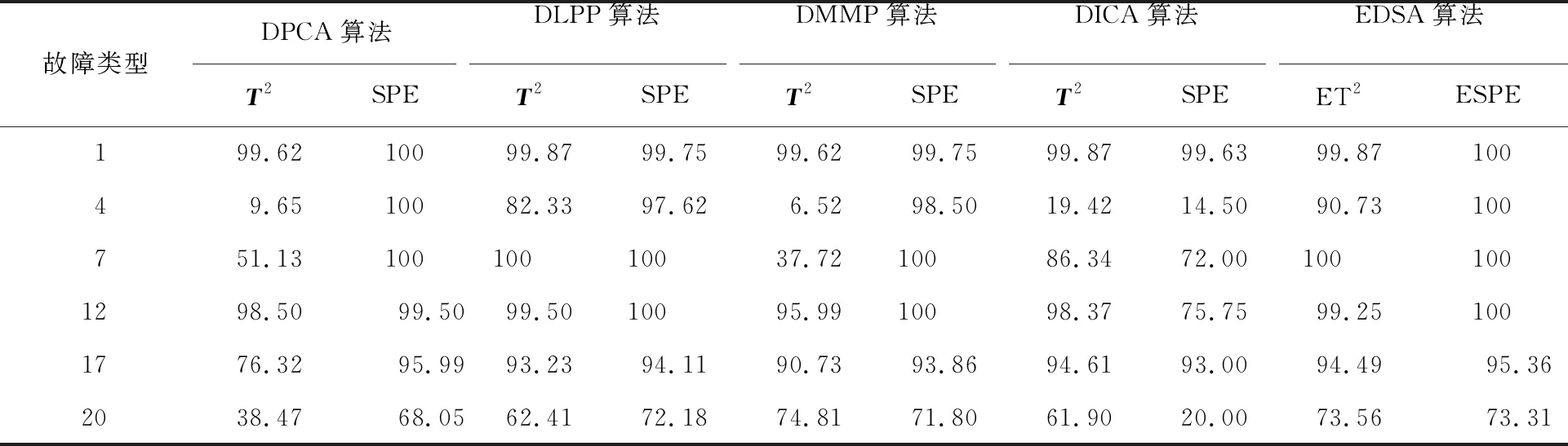
表3 5种算法对TE过程的故障检测率对比

3 结束语

新提出的基于集成动态结构分析的故障检测方案，引入了集成学习、贝叶斯推理和DMMP故障检测算法。集成动态结构建模考虑了所有可能的特征提取方式，通过DMMP算法将过程数据的邻域结构嵌入到局部和全局结构信息中，再通过集成学习方法将DPCA、DLPP和DMMP模型组合在一起。通过数值例子和TE过程验证了EDSA算法的有效性和可靠性，提高了动态过程的监测性能。然而，所提出的建模算法仍然是一种线性算法，如果将其应用于非线性过程的监测，可能无法达到预期的效果。考虑到在实际工业过程中存在许多非线性问题，所提出的检测算法还需向非线性扩展方向做进一步的研究。