安徽新安江流域生态补偿促进产业转型升级的门槛效应研究

万伦来, 张晗璐, 娜仁

(合肥工业大学 经济学院,安徽 合肥 230601)

0 引 言

跨省流域水资源保护是建设生态文明强国面临的重要课题,国家高度重视建立健全跨省流域水资源保护的政策措施,积极倡导实施生态补偿制度以统筹协调跨省流域各方利益主体的关系。2010年安徽新安江流域在全国率先实施生态补偿制度,以“禁、关、停、并、转”为抓手,积极推动以促进产业转型升级为重点、以强化经济高质量发展为导向的跨省流域生态环境保护系统工程,为全国跨地区生态环境保护提供了很好的学习借鉴。因此,有必要研究探明生态补偿促进产业转型升级的作用机制。

事实上,学术界已从不同角度揭示生态补偿与产业发展之间的内在关联性。文献[1]研究认为,生态补偿不仅能够保护生物多样性,而且还要保证为受偿区经济增长带来活力;文献[2]以我国丹江口水库南水北调中线水污染治理生态补偿为研究对象,指出生态补偿必须在最大限度保护水资源不受污染的同时,也要注重经济社会发展的公平性,兼顾受偿区经济可持续增长;文献[3]在研究长江经济带国家重点生态功能区生态补偿环境效率中发现,生态补偿具有促进受偿区产业转型升级的潜力;文献[4]研究指出,虽然新安江流域实施生态补偿短期内制约经济增长,但是长期来看，新兴产业的发展能够促进经济增长;文献[5]在研究成都市成甘工业园区实施横向生态补偿时发现,虽然此生态补偿对推动受偿区脱贫致富具有积极意义,但是也会产生诸如新贫困、产业发展趋缓等问题,从而对受偿区经济进一步发展产生制约。

综上可见,虽然已有学者关注到了生态补偿对产业转型升级及经济增长的正负面影响,但是并未考查其中正负面效应的量变和质变机制,即生态补偿对产业转型升级是否存在门槛效应。本文创新之处在于根据面板门槛模型特点,首次将区域异质性、补偿方式异质性纳入统一分析框架,深刻揭示生态补偿促进产业转型升级的微观发生机制。

1 门槛模型的构建

参考文献[6]的研究成果,构建两区制的门槛回归模型，即

(1)

其中:xit为由各种解释变量构成的m维向量;i=1,2,…,n;β1、β2为回归系数向量;qit为门槛变量;γ为门槛值;εit为随机扰动项,εit～iid(0,δ2)。将(1)式简化后可得:

(2)

其中,I(·)为指示函数。定义

则(2)式可进一步简化为:

yit=μi+βxi(γ)+εit

(3)

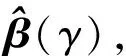
(4)

完成上述门槛回归的参数估计后,必须对门槛效应进行显著性检验,模型检验的原假设为H0:β1=β2,对应备择假设为H1:β1≠β2。构造检验统计量如下:

(5)

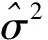
在接受原假设条件下,β1=β2,表明模型不存在门槛效应。拒绝原假设条件下,认为门槛效应存在,则继续对门槛估计值的真实性进行检验,即原假设为H0:γ=γ0,备择假设为H1:γ≠γ0。使用极大似然法检验门槛值,对应似然比检验统计量为:

(6)

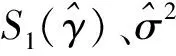
以上的参数估计和假设检验都是针对存在单门槛的情况,在实际的计量过程中会出现存在多门槛的情况,多门槛模型可以据此进行扩展。

2 数据来源、变量说明与模型设定

2.1 数据来源

本文选取安徽新安江流域为研究对象。考虑数据统计口径一致性和可比性,本文主要以黄山市下辖徽州、屯溪、黄山3个区和歙县、休宁、黟县、祁门4个县共7个区县为考查样本,剔除了宣城市下辖的绩溪县。

本文所有数据来源于《安徽省统计年鉴》《黄山市统计年鉴》《新安江流域上下游横向生态补偿试点实施情况评估报告》。考虑到回归模型的自由度,本文使用EVIEWS10.0低频数据转化高频数据的方法,将年度数据转化为季度数据以满足计量分析的需要。

2.2 变量说明

(1)被解释变量。产业转型升级(LTS)参考文献[8-9]的研究成果,本文采用第三产业产值与第二产业产值之比作为产业转型升级的度量。

(2)核心解释变量及门槛变量。一是总体生态补偿LSEC;二是输血型生态补偿LTEC;三是造血型生态补偿LCEC。此部分是由实地调研数据所得。本文依据当地生态补偿实情和从《新安江流域上下游横向生态补偿试点实施情况评估报告》中整理获取的相关材料,将政府有关生态补偿的财政支出划分为输血型生态补偿与造血型生态补偿两大类型。另外,考虑到安徽新安江生态补偿的主要补偿形式为资金拨付,因此本文选择生态补偿资金投入数额来代表生态补偿,并使用stata15.0计算其存量数据。

(3)控制变量。一是金融发展程度LFD,本文参考文献[9]的研究成果用各区县存贷款余额与GDP之比来衡量;二是产业规模LSCAL,本文参考文献[10]的研究成果用各区县全社会固定资产投资衡量;三是外商直接投资LFDI,本文参考文献[10]的研究成果,利用2010—2018年中美年均汇率换算各区县外商直接投资额为以人民币为货币单位的相应数值衡量。

根据以上各变量定义说明,本文得到各变量的统计性描述见表1所列。

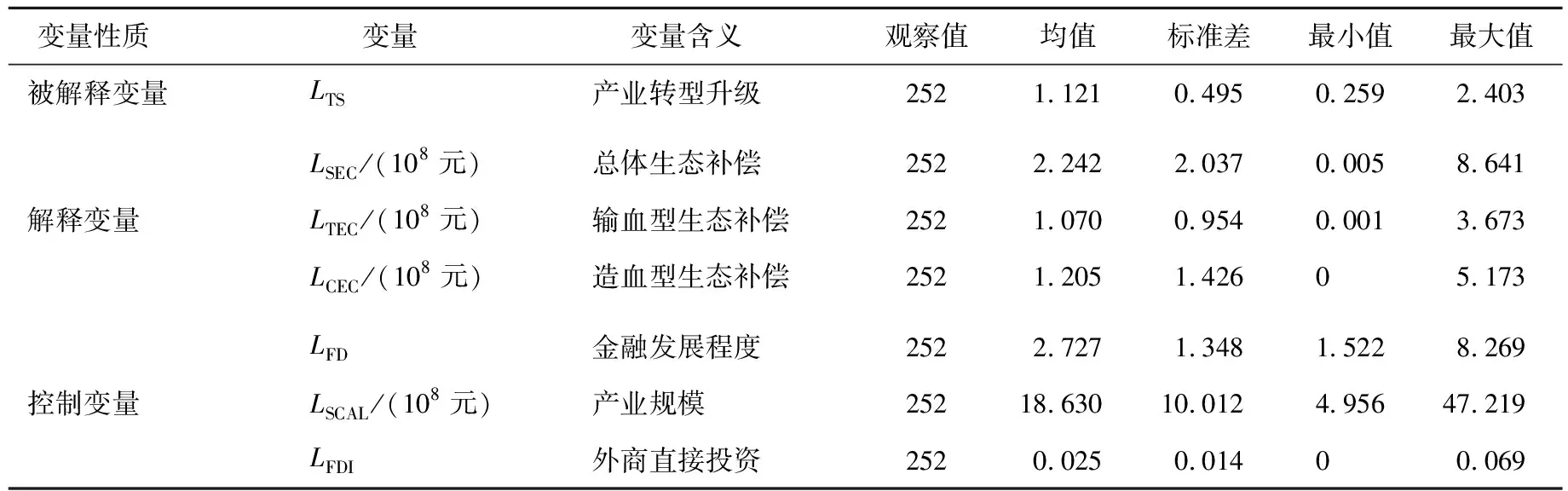
表1 变量的统计性描述

2.3 模型设定

为验证上文研究假设,本文拟分别以输血型生态补偿、造血型生态补偿为核心解释变量,以产业转型升级为被解释变量构建计量模型(7)、模型(8)。

同时以总体生态补偿和造血型生态补偿为核心解释变量和门槛变量,以产业转型升级为被解释变量构建门槛回归模型(9)、模型(10)。

为避免异方差和多重共线性,本文对变量进行取对数处理,具体模型构建如下:

lgLTSit=α0+α1lgLTECit+α2lgLControl it+σit

(7)

lgLTSit=α0+α1lgLCECit+α2lgLControl it+σit

(8)

lgLTSit=μi+β11lgLSECitI(lgLSECit≤γ1)+

β12lgLSECitI(lgLSECit>γ1)+

β13lgLControl it+εit

(9)

lgLTSit=μi+β21lgLCECitI(lgLCECit≤γ2)+

β22lgLCECitI(lgLCECit>γ2)+

β23lgLControl it+εit

(10)

其中:i为考查样本;t为考查时期;LTSit为产业转型升级;LSECit为总体生态补偿;LTECit为输血型生态补偿;LCECit为造血型生态补偿;LControl it为一系列控制变量;I(·)为指示函数,当括号内表达式为真时,其值为1,反之为0;σit、εit为随机扰动项。

3 实证分析

3.1 平稳性检验

数据的平稳性是后续进行面板回归分析的基础,为此依据本研究的数据类型采用同根检验(levin-lin-chu test,LLC)法进行单位根检验,具体检验结果见表2所列。

由表2可知,取对数之后的产业转型升级、总体生态补偿、输血型生态补偿、造血型生态补偿、金融发展水平、产业规模和外商直接投资均为平稳序列。

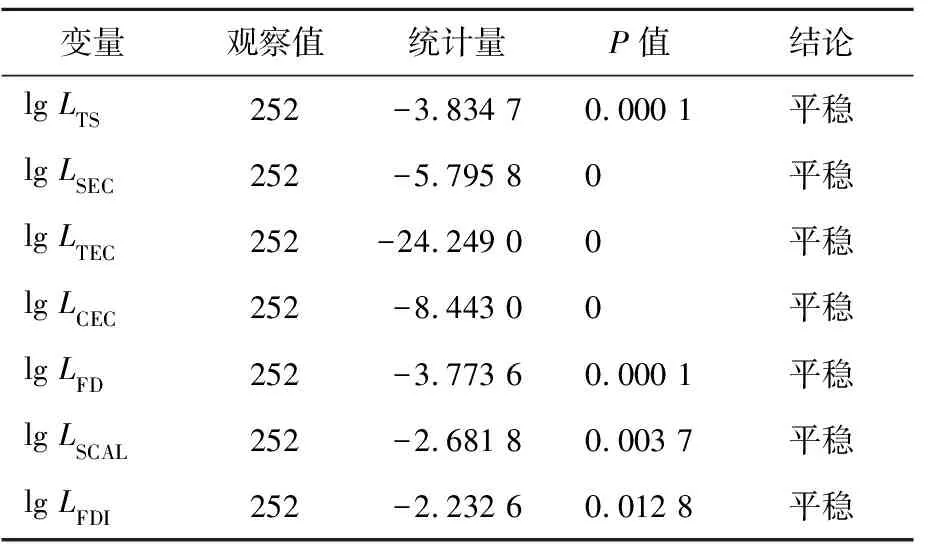
表2 变量的LLC单位根检验

3.2 非线性面板门槛回归分析

为得到非线性面板门槛回归结果,首先必须对核心解释变量和门槛变量进行显著性检验,因此本文将相关变量代入模型(9)并采用stata15.0进行分析,以生态补偿LSEC为核心解释变量和门槛变量的显著性检验结果见表3所列。表3中,P值和临界值均是采用“Bootstrap法”反复抽取1 000次得到的结果。由表3可知,单门槛效应在 1% 的显著性水平下显著,双门槛效应和三重门槛效应在各显著性水平下均不能通过检验,表明以生态补偿SEC作为门槛变量拒绝线性关系的原假设,这说明生态补偿对产业转型升级确实存在门槛效应,同时也说明可选用单重门槛面板模型估计其门槛值。

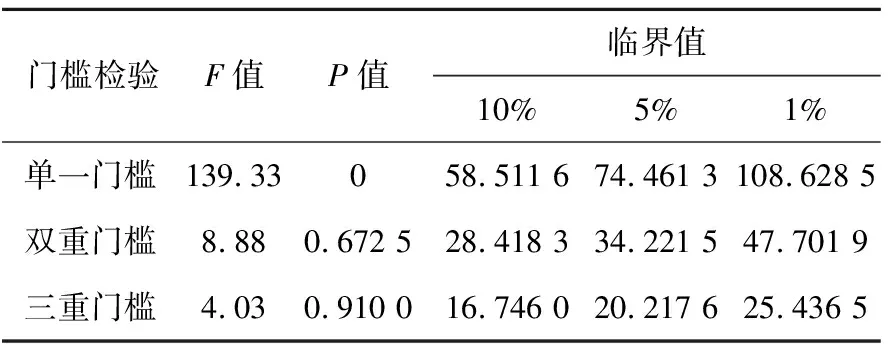
表3 lg LSEC为门槛变量的门槛值估计与检验结果

根据以上检验结果,运用单重门槛面板模型进行门槛值估计,结果见表4所列。由表4可知,安徽新安江流域实施生态补偿促进产业转型升级门槛值为0.873 1,经过指数运算还原得到基于区县层面的门槛值存量为2.394 4×108元,95%置信区间为[0.842 5,0.880 1],经过指数运算还原基于区县层面95%置信区间值为[2.322 2,2.411 1]。

在进行核心解释变量、门槛变量的显著性检验和进行门槛值估计之后,本文根据模型(7)得到该地区实施生态补偿与产业转型升级的门槛估计(见表4)。从表4可以看出,该地区实施生态补偿促进产业转型升级具有显著的门槛特征,其中,当区县层面生态补偿资金投入存量低于门槛值2.394 4×108元时,即该地区生态补偿总体投入资金存量未达到16.760 8×108元时,其影响系数为-0.047 5,并在1%的显著性水平下通过检验,说明此时生态补偿资金投入对当地产业转型升级具有明显的阻碍作用;当区县层面生态补偿资金投入存量高于门槛值2.394 4×108元,即该地区生态补偿总体投入资金存量达到16.760 8×108元后,生态补偿资金投入对产业转型升级的影响系数发生方向性改变变为0.190 8,并在1%的显著性水平下通过检验,说明此时生态补偿对产业转型升级的影响由抑制作用转变为促进作用。

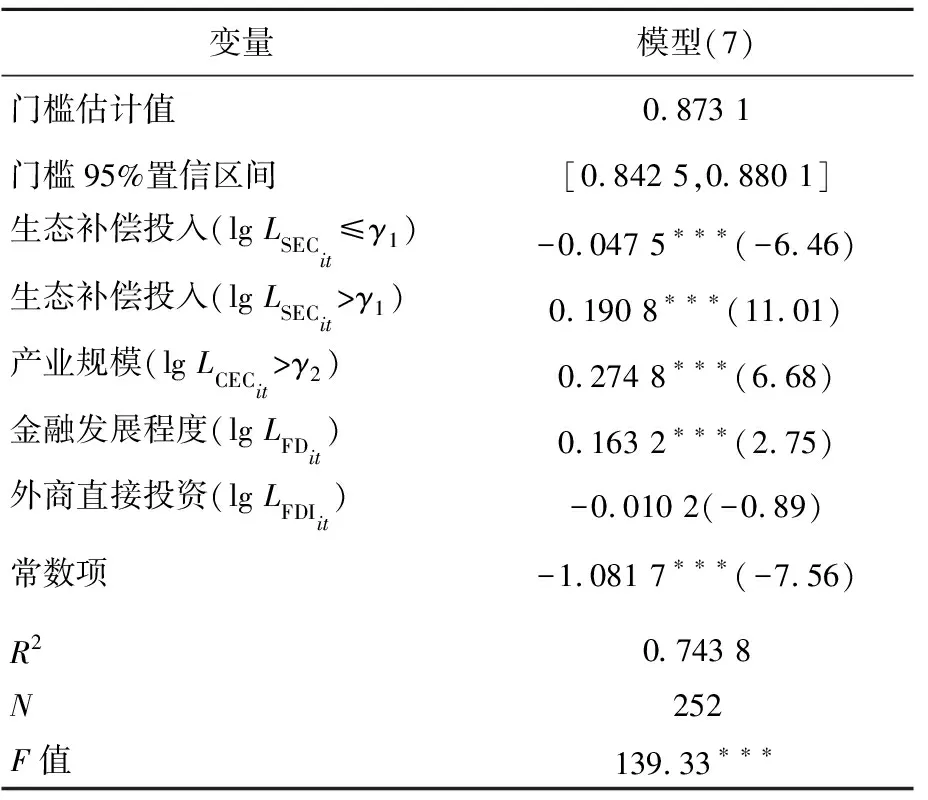
表4 全地区面板门槛模型回归结果

3.3 稳健性检验

为考察估计结果的稳定性和所得结论的可靠性,本文参考文献[11]逐一加入解释变量进行回归的方法对门槛模型进行显著性检验,得到模型(8)～模型(10),稳健性检验结果见表5所列。

由表5可知,模型(7)～模型(10)均通过单重门槛的显著性检验,核心解释变量及重要控制变量对产业转型升级的显著性基本没有发生变化,而且R2随着控制变量的增加而增大。因此,本文认为上述门槛回归结果具有稳健性,结论是可靠的。

表5 稳健性检验

上述研究结果表明,生态补偿促进产业转型升级的确存在一个门槛值,门槛值之前生态补偿投入抑制当地产业转型升级,门槛值之后由抑制转为促进。

3.4 区域异质性分析

本文将总体样本按地理位置划分为中心城区(包括徽州区、黄山区、屯溪区、歙县)和非中心城区(包括休宁县、黟县、祁门县)2个子样本分别进行门槛回归。

回归结果见表6所列。

表6 分区域门槛回归结果

中心城区和非中心城区2个子样本回归即模型(7)-中心城区、模型(7)-非中心城区的回归结果显示,2个子样本达到门槛值后生态补偿对产业转型升级的影响系数存在明显差异。

在达到门槛值之后中心城区生态补偿对产业转型升级的影响系数为0.224 5,而非中心城区的影响系数仅为0.072 8,这表明该地区生态补偿对产业转型升级的影响作用存在空间异质性,且中心城区生态补偿对产业转型升级的促进作用明显高于非中心城区。

3.5 补偿方式异质性分析

为验证不同补偿方式对当地产业转型升级的异质性影响,将相关变量带入模型(7)-中心城区、模型(7)-非中心城区,即分别以输血型和造血型生态补偿为核心解释变量，运用固定效应模型进行回归分析,具体结果见表7所列。

表7 固定效应回归结果

由表7可知,输血型生态补偿在1%的显著性水平下抑制当地产业转型升级,而造血型生态补偿对产业转型升级的影响不显著。事实证明补偿方式不同对产业转型升级的影响具有异质性,为进一步探究造血型生态补偿促进产业转型升级是否也呈现U型态势,本文继续以造血型生态补偿为核心解释变量及门槛变量进行门槛回归分析。lgLCEC为门槛变量的门槛值估计与检验结果见表8所列。由表8可知,单门槛效应在 1% 的显著性水平下显著,即造血型生态补偿促进产业转型升级亦存在单重门槛。

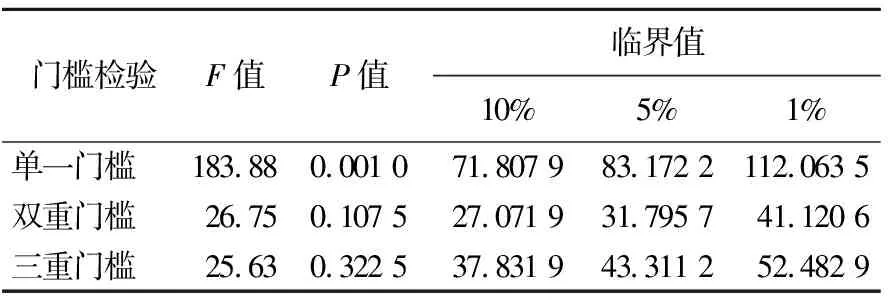
表8 lg LCEC为门槛变量的门槛值估计与检验结果

面板门槛模型回归结果见表9所列。由表9可知,造血型生态补偿在门槛值之前,对产业转型升级影响不显著,门槛值之后促进作用较为明显,与总体生态补偿促进产业转型升级呈现U型态势保持一致,更能说明生态补偿政策促进产业转型升级,造血型生态补偿起到决定性的主导作用。也就是说,不同补偿方式对产业转型升级的促进效应不同,输血型生态补偿对产业转型升级影响不显著,造血型生态补偿对产业转型升级呈现先抑制后促进的U型态势。

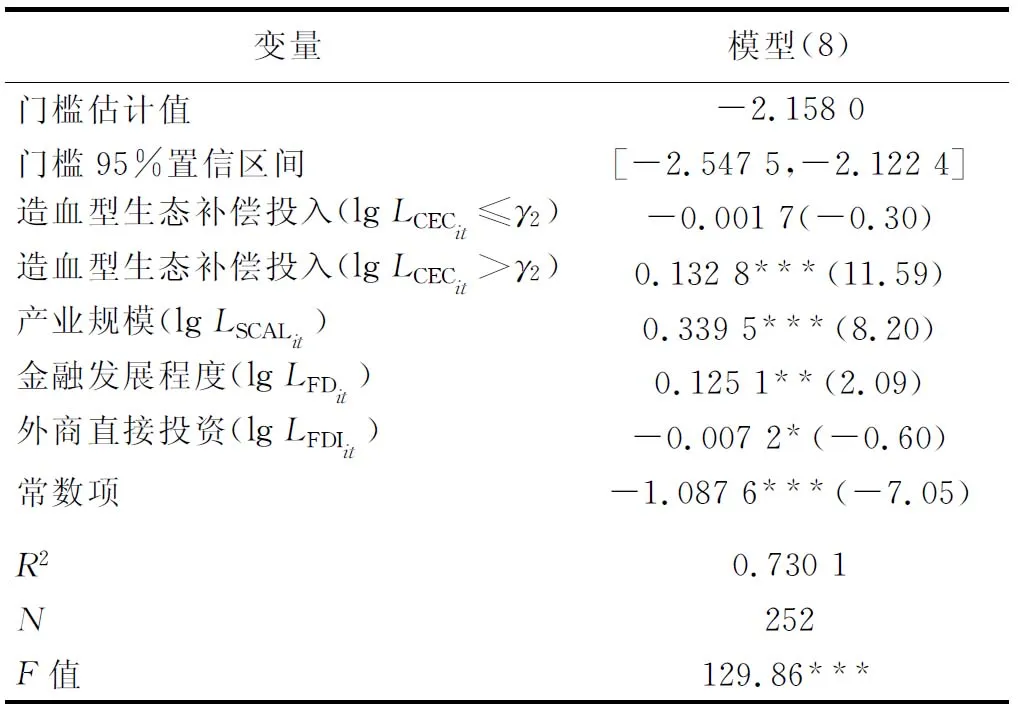
表9 面板门槛模型回归结果

4 结 论

本文基于2010—2018年新安江流域安徽段7个区县面板数据,运用门槛回归模型验证了该地区生态补偿财政支出对其产业转型升级作用存在显著的单一门槛特征。政府生态补偿财政支出对于产业转型升级的影响可分为2个阶段:当生态补偿整体财政支出存量小于16.760 8×108元时,对产业结构升级呈现抑制作用;当生态补偿整体财政支出存量大于16.760 8×108元时,对产业结构升级呈现促进作用。此外,该地区生态补偿对产业转型升级的影响作用存在区域异质性和补偿方式异质性。空间异质性说明经济发展水平相对较好的中心城区的生态补偿财政支出对产业转型升级促进作用要明显高于经济发展水平相对较差的非中心城区。补偿方式异质性说明造血型生态补偿财政支出达到门槛值之后对当地产业转型升级、促进经济高质量发展能起到显著作用。