电路分区自比较的硬件木马检测方法

徐 皓, 易茂祥, 金礼玉, 梁华国, 鲁迎春

(合肥工业大学 微电子学院,安徽 合肥 230601)

硬件木马(hardware Trojan,HT)是电路安全攻击者为了达到改变集成电路(integrated circuit,IC)功能或性能、泄漏敏感信息等非法目的而在电路中植入的恶意硬件模块。近年来,HT攻击在硬件安全领域引起了广泛关注。当今IC专业分工的设计与制造模式所导致的一个后果是在设计或制造过程中电路面临着HT植入的风险,这是由于任何能接触到设计或制造并熟知电路的人都可能对电路进行恶意的修改。因此,对芯片设计阶段或制造后进行HT检测是十分重要和必要的。

目前,有很多针对芯片设计或制造阶段的HT检测方法,包括逆向工程、逻辑测试、旁路分析等。逆向工程[1-2]需要对芯片进行破坏性的解封装,整个过程代价昂贵且耗时,使得该方法的应用受到很大局限；逻辑测试[3-5]方法在面对触发结构和功能都很复杂的HT时,不能有效获得HT激活向量而实现检测；旁路分析法[6-10]在当今纳米级的设计与制造水平下,工艺变化(process variation,PV)将导致同类芯片间的旁路特征出现较大的差异,使HT引起的旁路信号变化可能被PV所覆盖,造成HT检测失败。从PV影响HT检测结果的角度来看,基于门级特性描述(gate-level characterization,GLC)的HT检测方法[11-15]具有较明显的优势,它将PV引起的电路特征变化作为电路的一种固有属性,将电路中每个门受到的PV影响与一个比例因子对应起来,通过比例因子与门的额定功率或延时相乘,实现在功率或延时的变化上对PV建模。通过测量各种输入条件下的电路总功率或路径延迟,得到以比例因子为变量的线性方程。HT的存在将导致方程求解结果的比例因子产生异常,利用这种比例因子的异常值即可实现对HT的检测。通常基于GLC的HT检测方法需要对每个门进行精确的GLC刻画,这对于大规模的待检测电路来说是非常复杂和耗时的;同时,采用传统的GLC方法所得到的众多比例因子并不能直接用于识别HT导致的电路指标异常,而需要引入黄金模型进行比较,从而完成HT检测。但黄金模型的获取难度大、成本高,因此需要解决基于GLC的HT检测方法对黄金模型的依赖性以及检测效率低下的问题。

本文在传统的基于GLC木马检测方法的基础上,提出利用电路分区后计算并直接利用各区域木马比例因子自比较的方法,实现无需黄金模型约束条件下的电路HT检测。

1 相关研究工作

为了解决基于GLC的HT检测方法对于黄金模型依赖的问题,文献[14]、文献[15]分别提出了相应方案。文献[14]将电路划分为2个区域,约束条件要求2个区域共同包含1个重叠的门电路;采集分区后的泄漏功耗,对不同分区分别求解重叠门电路的比例因子,若两者的比例因子存在差异,则判定其中一个区域植入了HT;但该方案在实现重叠门的筛选技术上存在较大的难度。文献[15]提出将电路分成多个区域及时钟树区,每个分区电路比例因子的求解需要包含时钟树区,将不同分区下的时钟树区比例因子进行比较,作为判断HT存在与否的依据；同时,为防止时钟树区植入HT导致误判,引入3条判定HT存在的规则。

针对以上基于GLC的HT检测方法存在的不足,本文提出一种基于GLC与电路分区泄漏功耗测量的HT检测方法。该方法根据电路各区域每个门的标准泄漏功耗和划分后测量到的各区域实际泄漏功耗构成线性回归方程,通过相应的回归分析求解回归方程，得到各分区电路的木马比例因子,该因子是可以直接反映木马泄漏功耗的参数;将各个区域的木马比例因子进行自参照比较,可以直接实现HT的检测。本文方法在消除黄金模型依赖的同时采用分区电路木马比例因子自比较的方式,有效提高了HT的检测效率。

2 电路分区自比较方案的木马检测原理

2.1 电路泄漏功耗的门级特性描述

IC生产制造过程中的PV是由于在制造过程中对小的特征技术无法做到精确控制,生产的IC技术指标与实际参数测量值之间存在偏差,其中PV影响最大的是电路中的阈值电压和有效沟道长度。工艺带来的这2个参数的变化将影响IC的一些特性参数,如传播延迟和泄漏功耗,导致它们偏离设计值[14]。

GLC是根据器件物理特性(如有效沟道长度)或电路特性(如传播延迟、泄漏功耗)来表征IC每个门的特征过程。其中泄漏功耗适用于HT检测,由于植入的HT无论是否激活都会产生额外的电路泄漏功耗,这使得检测出那些复杂且难以触发的隐蔽HT成为可能。设Pleak,j表示电路中门j的标准泄漏功耗,Pleak,j′表示门j的实际泄漏功耗,令Pleak,j′=sjPleak,j,引入比例因子sj用于描述由于PV所导致的标准泄漏功耗与实际泄漏功耗之间的比值。因此,可以按照下式计算出整个电路(设共N个门电路)实际泄漏功耗与各个门标准泄漏功耗之间的关系，即

(1)

电路输入的激励不同,所处的状态也不同,此时各个门的泄露功耗也会有所差别,而比例因子sj通常被认为不会发生改变。文献[15]针对输入激励的改变是否影响比例因子sj的问题进行了相应的蒙特卡罗仿真分析，将一个1位全加器的各个门置于不同的输入模式下,测量实际泄露功耗与标准泄露功耗,并计算它们之间的比值。结果表明,对于电路的不同状态,电路泄露功耗的比例因子sj基本保持不变,因此电路总泄漏功耗在输入向量vi情况下可以表示如下:

(2)

其中:Pleak(vi)为输入向量vi激励下的电路的总泄漏功耗;sj为第j个门的比例因子;Pleak,j(vi)为第j个门的标准泄漏功耗(1≤j≤n)。由(2)式可知,电路在不同输入状态下的总泄露功耗只与相应输入状态下各个门的标准功耗相关,而每个门对应的比例因子不变。但非法植入电路的HT,不论是否激活都会产生额外泄露功耗,这样势必会打破(2)式的平衡。用PHT来表示所植入HT的泄露功耗,可以得到:

(3)

将多个不同输入激励条件下得到的(3)式构成方程组,用于求解具体的比例因子,输入激励的数量需要大于电路中门的个数,以满足方程组的非相关性,完成求解。HT引起的额外泄漏功耗将导致实际求解的比例因子sj相较于实际比例因子值存在异常,因此可以通过识别比例因子的异常实现对HT的检测。而要构成和求解上述方程组,需要不同输入激励下实际的泄露功耗和标准的泄漏功耗数据。目前市场上一些测量仪器可以实现对功耗极低误差的测量,如有些仪器的测量单元能将误差降到10-4～10-5。因此,可以利用仪器完成实际泄漏功耗的采集,而电路中门的标准泄漏功耗在相应的工艺库里都有定义,电路标准泄漏功耗通过设计仿真工具能够获得。

2.2 多元线性回归

因为电路的标准泄露功耗和实际泄露功耗可以在设计阶段和实际测量中获得,所以能计算出各个门的比例因子sj。若此时电路中植入了木马,引起额外的泄漏功耗,比例因子sj的值会表现异常,但由于门的数量众多,微小的差异反应到每个比例因子上很难直接识别。因此,本文为方便木马的鉴别,额外设置s0=PHT,表示木马比例因子,单独反映木马引起的泄漏功耗。对于木马比例因子s0的求解恰好是多元线性回归的过程,将不同输入激励条件下得到的(3)式构成一组线性回归方程,通过回归分析求得木马比例因子s0的值,并根据其是否异常来判断HT是否存在，则有：

Ptol=s0Im+s1P1+s2P2+s3P3+…snPn+ε

(4)

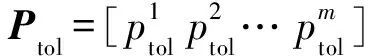
s1pi,1-s2pi,2-…-snpi,n)2

(5)

(6)

(7)

S=(PTP)-1PTPtol

(8)

(5)式表示均方误差;n个向量Pj加上向量Im构成m×(n+1)维矩阵P=[ImP1P2…Pn],将(5)式简化为矩阵形式,如(6)式所示;当均方误差J(S)对参数sj的偏导数为0时取极值,此时均方误差最小,线性回归参数sj可以得到最优解S=[s0s1s2…sn]T, 如(7)式所示;将(7)式中的项重新排列,得到向量S的标准求解式(8),比例因子sj(1≤j≤n)和木马比例因子s0可根据(8)式求解获得。即使一些回归方程构成的(PTP)-1不可逆,仍可通过奇异值分解计算(PTP)-1的伪逆,从而得到向量S。

2.3 电路分区自比较的木马检测

理想情况下,无HT正常电路的木马比例因子s0等于0,而当电路植入有HT时,s0将是一个不等于0的异常值。但在实际情况下,由于测量误差的存在,无HT电路的木马比例因子s0并不是理想地等于0,也就不能通过s0值是否为0来判断HT的植入。但是如果预先确定了无HT植入时电路木马比例因子s0的标准值,进而进行比较以判断是否存在HT,那么就仍然需要依赖黄金模型。为此,本文提出的方法将待测电路分成多个区域,对每个区域进行泄露功耗的门级特征描述,再采用线性回归分析求解,得到各区域的木马比例因子。对于无HT植入的电路,这些区域间的木马比例因子值差异不大,但如果电路的某区域存在HT的植入,则该区域的s0值将明显异常于其他区域的s0值,可以直观地判断出HT的存在且定位其所在的区域。除此之外,分区后的区域电路内逻辑门数量减少,有利于降低求解计算工作量,同时也可以提高HT的检测精度。

3 木马检测方法的实现

3.1 检测方案应用实例

本文以ISCAS’85的C17电路为例,演示本文检测方法实现HT检测的过程。C17电路由6个与非门组成,将C17电路划分为2个区域,其中区域1植入简单的HT(非门),如图1所示。

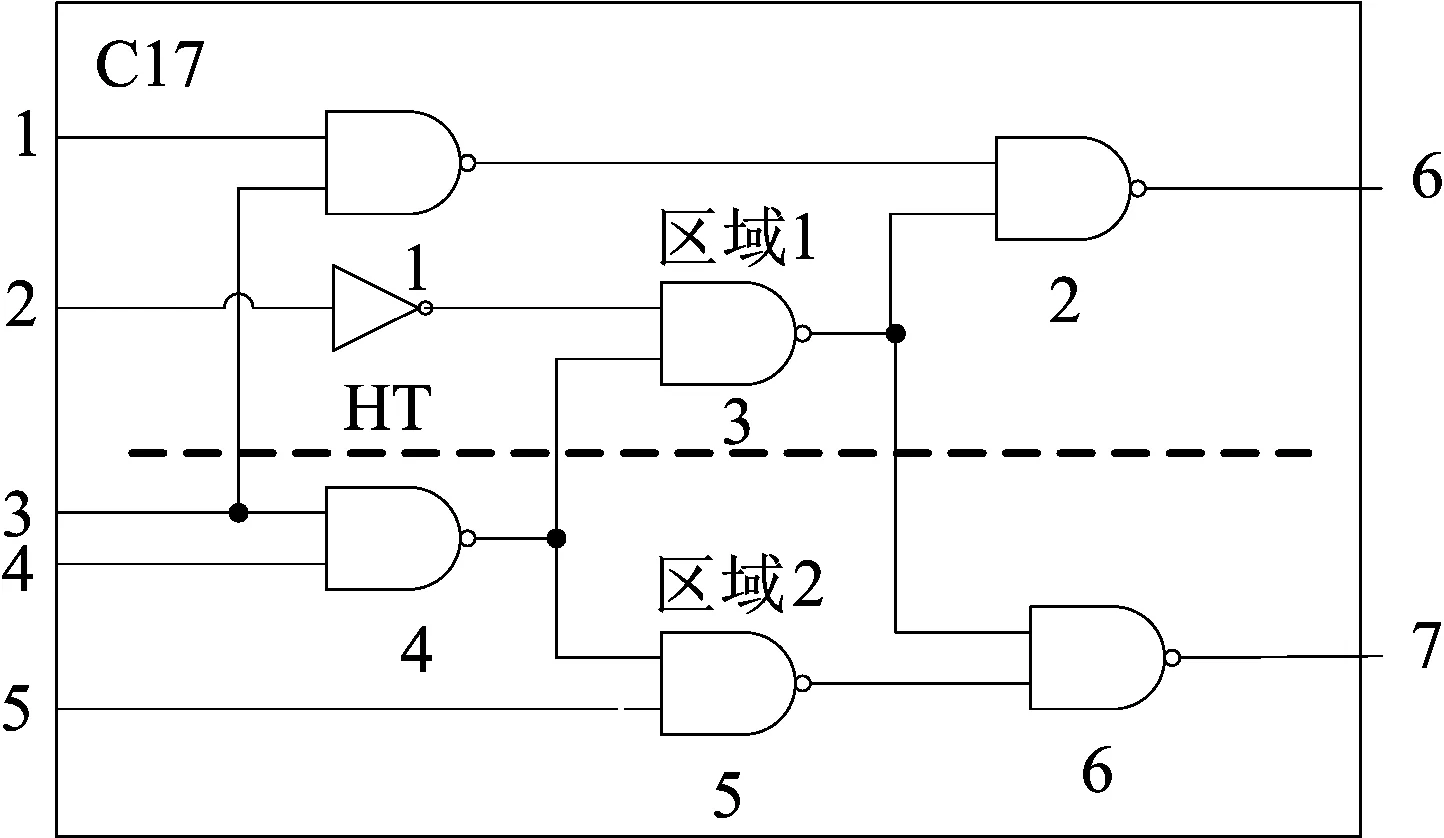
图1 电路C17

通过Innovus软件仿真得到无HT植入时C17电路各个门的标准泄漏功耗,结果见表1所列。在电路区域1中植入木马,再次仿真,利用PV模型来模拟统计电路植入HT后2个区域的实际泄漏功耗,结果见表2所列。

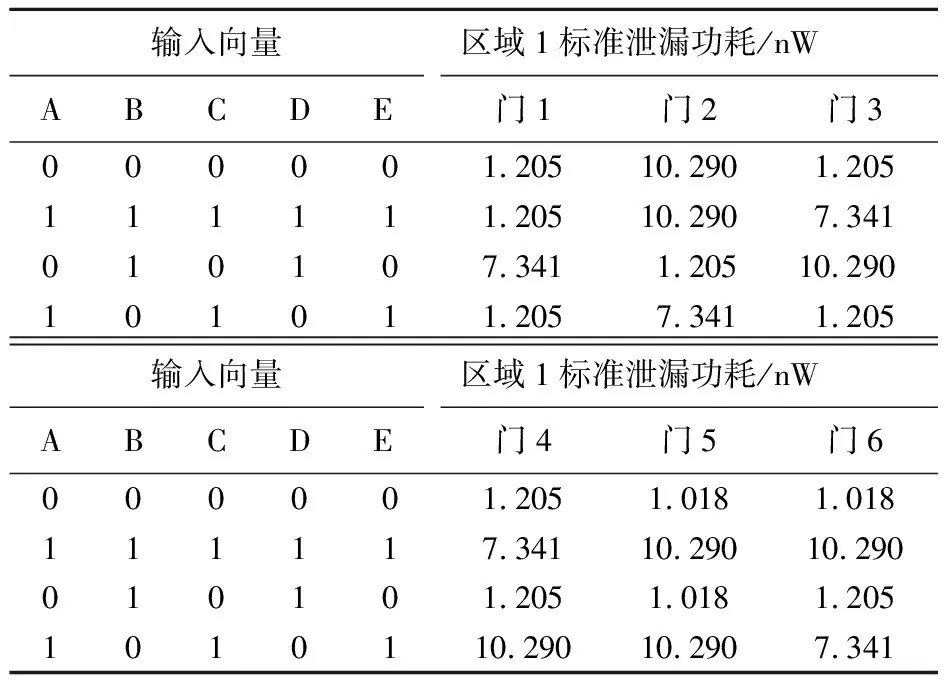
表1 C17电路各个门的标准泄漏功耗

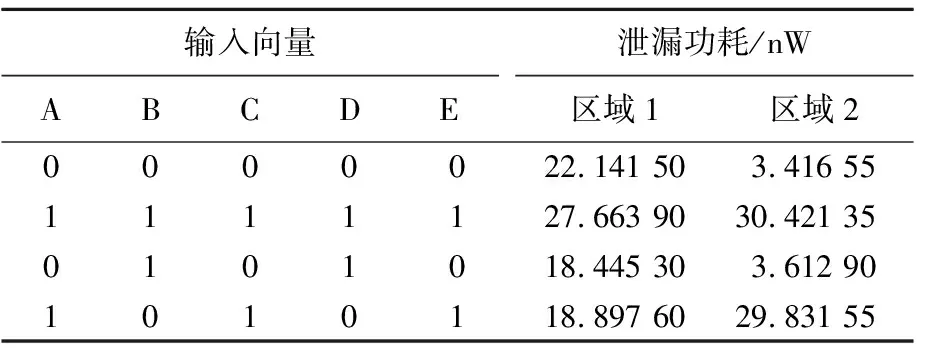
表2 区域1和区域2的总泄漏功耗

利用获得的泄漏功耗数据构成线性回归方程,区域1的P、Pto1为：

(9)

区域2的P、Pto1为：

(10)

按照(8)式求解可得向量S=[s0s1s2s3],结果见表3所列。其中：s0为木马比例因子,反映木马泄漏功耗;s1、s2、s3为普通逻辑门的比例因子。此时,若将2个区域普通逻辑门的比例因子进行比较,则很难识别出异常的区域；而若直接比较2个区域的木马比例因子s0的值,则可以观察到由于HT植入了区域1,导致该区域的s0值明显异常,于是判断该电路在区域1中植入了HT。

表3 区域1和区域2的比例因子值

3.2 检测方法的实施流程

整个检测方法的实施流程如图2所示。首先对待测电路进行分区,建议电路设计人员在完成芯片原始电路功能设计后,将电路按照一定的规则划分成多个区域,可以根据不同的时钟域和不同的功能模块来划分,每个区域包括1个或多个功能模块;给划分后的每个电路分区添加电源门控单元,各区域的供电电源受电源门控单元控制可随意开关,不受其余区域的影响,通过这样的方式可以方便待测电路目标区域泄漏功耗的采集;获取IC的标准泄漏功耗和实际泄漏功耗数据,每个门在不同输入激励下的标准泄漏功耗可以通过电路仿真获得,而每个区域实际泄漏功耗的采集,需要利用电源门控模块使其他区域的电源处于关闭状态,再根据不同输入激励条件测量得到对应区域的电路总泄漏功耗,随后切换电源门控模块测得所有区域的电路总泄漏功耗。最后,根据得到的IC各区域电路的泄漏功耗构成线性回归方程,并进行回归分析,求得每个区域的木马比例因子。

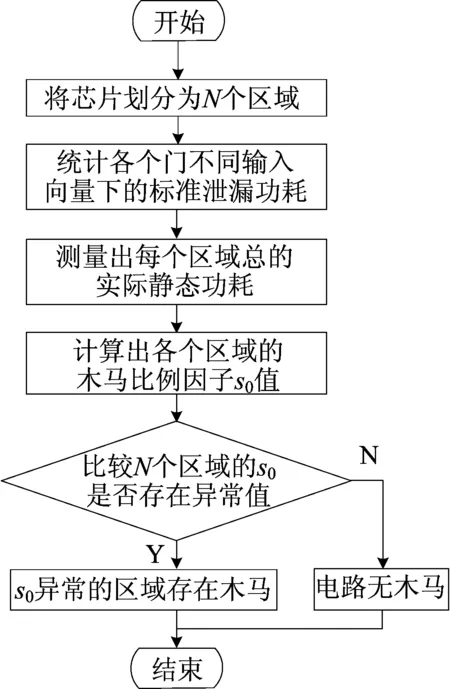
图2 木马球检测方法流程

假设待测电路分成了N个区域,则可以得到N个木马比例因子s0,通过直观比较这些比例因子数据,判断某区域的木马比例因子是否存在异常,实现HT的检测与定位。

4 实验结果与分析

通过实验将本文方法的实施流程应用于ISCAS’85基准电路,分别对无HT植入和有HT植入的电路进行仿真。基于Nangate45nm单元库,利用Cadence Innovus对基准电路的网表进行物理设计,通过功率仿真分析获得电路中的标准泄漏功耗数据,然后利用PV模型模拟电路总泄漏功耗。利用MATLAB工具对得到的泄漏功耗数据进行处理,选择非相关性输入激励,构成线性回归方程,并通过回归分析求解每个区域的木马比例因子s0。实验中对基准电路采用4分区和10分区,目的是为了实现HT所在区域的判断,也可以探讨不同数量的分区对实验结果的影响。

实验将基准电路S298分别划分为4个区域和10个区域,划分时保证各区域的门数大致相等。均在区域1中植入非门HT，根据获取的泄漏功耗计算得到电路区域的木马比例因子s0,结果见表4、表5所列。从表4、表5可以看出：区域1中的s0相较于其他区域明显异常,故以此判断区域1植入有HT;而采用10个分区的实验中,区域1与其他区域的木马比例因子差值更大,说明分区越多可检测木马比例因子差异越高。

表4 4分区下S298电路木马比例因子

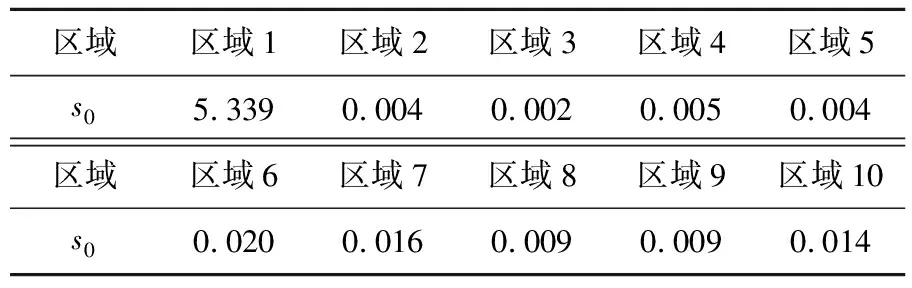
表5 10分区下S298电路木马比例因子

实验同时按照4分区划分对基准电路S344、C499、C880、C3540和C6288进行方案应用,结果如图3a所示,其中S344电路是需要规模由小到大的电路进行实验对比。实验预先在每个电路的分区1中植入HT(非门),从图3a可以看出,分区1的木马比例因子明显高于其他分区,而且随着电路尺寸增加,含HT与不含HT区域的木马比例因子差异性缩小,检测能力降低。

对基准电路采用10分区划分时的实验结果如图3b所示。从图3b可以看出,分区数量的增加提高了方案的HT检测能力。虽然电路规模扩大也会增加HT的检测难度,但观察发现仍然能够根据区域1中的木马比例因子明显异常,判断HT的存在和位置。

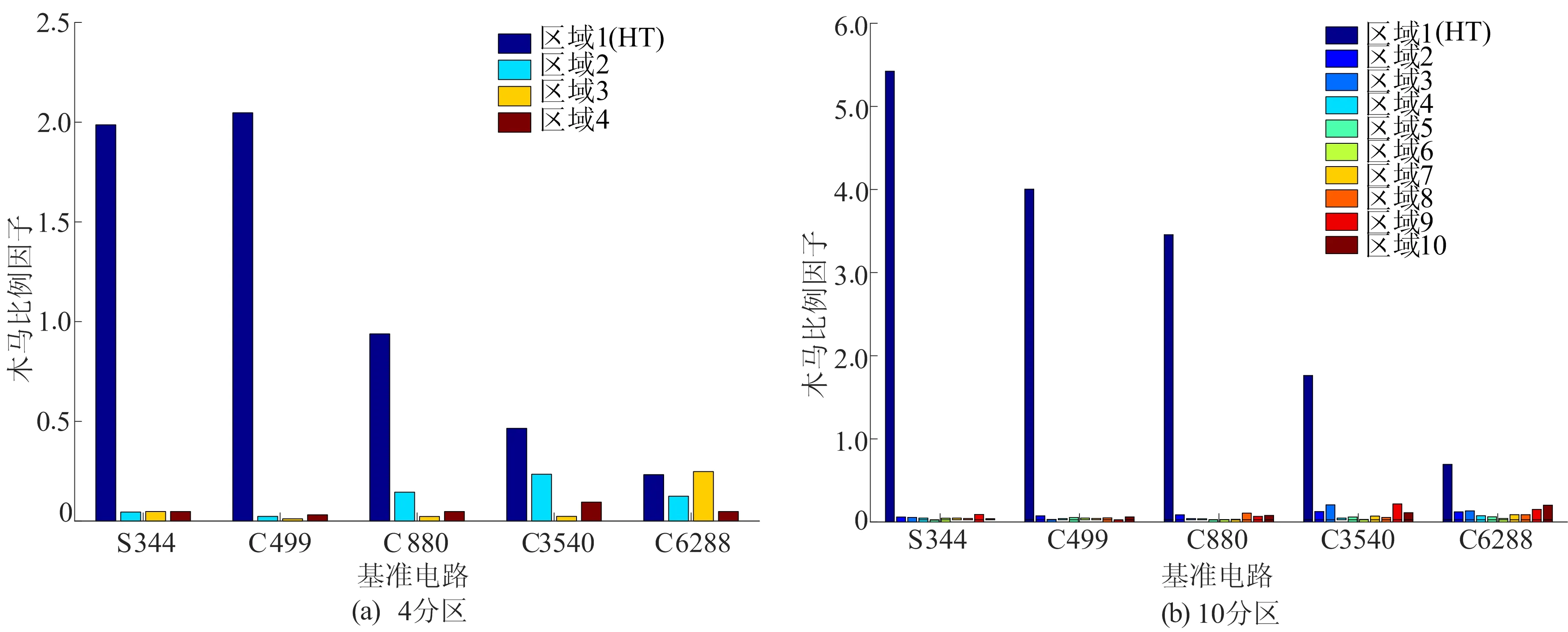
图3 不同分区下基准电路的木马比例因子

2种不同电路分区情况下,基准电路植入HT区域与无HT区域的木马比例因子差值变化情况如图4所示。从图4可以看出,相较于4区域划分,采用10区域划分基准电路可比较的木马比例因子差值更大,更有利于实现HT的检测。

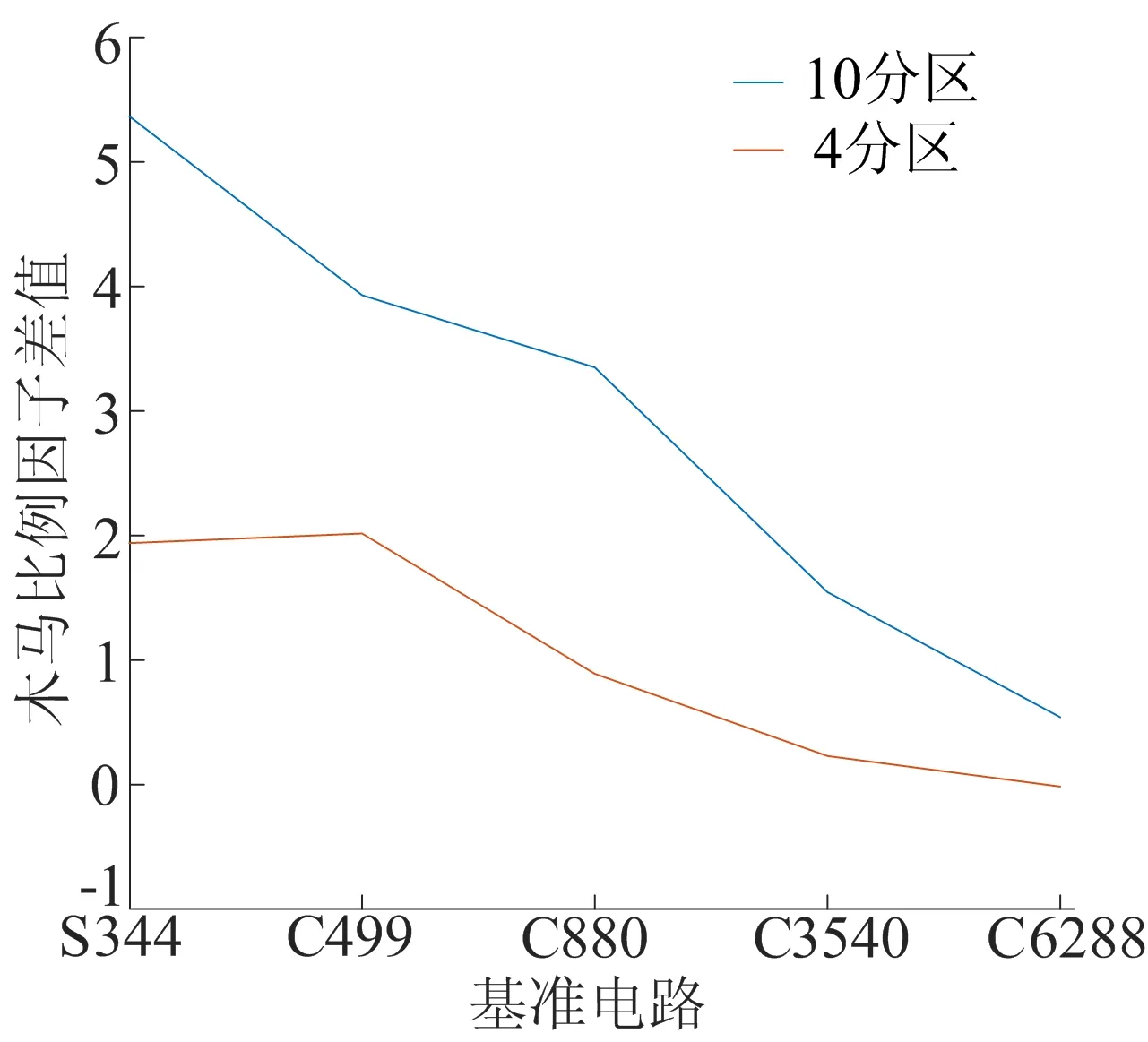
图4 2种分区下各基准电路木马比例因子差值

从上述实验结果可以发现,对于同一个待测电路,检测方案中对电路的分区越多,HT产生的泄漏功耗在所在区域泄漏功耗的占比越大,对木马比例因子的影响也越大,方案的检测能力就越强。同时,随着电路规模的扩大,HT引起的泄漏功耗相较于整个电路泄漏功耗占比减小。因此需要对电路进行更多的划分以提高检测能力。但分区增加会导致计算量增高,导致检测成本增加。

根据C6288的实验结果：在10分区情况下,可以通过不同区域木马比例因子的差异实现对单非门HT的检测；而采用4个分区时,区域木马比例因子差异已经无法识别,使HT的检测变得困难。这是由于C6288包含的逻辑门门数达到2 406个,而HT门为单个非门,占比低于0.04%。实验结果表明：当HT电路超过总电路规模的0.04%时,可以实现对电路中HT的良好检测。

本文方法用于更大更加复杂的待测电路时,可以采用更多分区划分来保证HT的检测能力。近几年发表的基于电流、功率分析的HT检测方法的实验结果与本文方法实验结果的检测参数、可检测木马占比、木马定位等性能的比较见表6所列。其中：检测参数包括功耗或电流;可检测木马占比表示可检测HT电路的大小占待测电路的比例;定位指是否可确定HT所在待测电路的划分区域。

文献[16]基于多电源瞬态电流分析,引入黄金模型比较待测芯片的总电源电流差,当超过预定义的阈值时判定HT的存在;文献[17]通过持续向量应用,放大黄金模型和待测芯片的功率分布差异,根据差分功率轮廓分布的信息来判断电路有无HT植入及其位置;文献[18]根据泄漏电流参数,利用线性回归求解门级电路比例因子,按照其平均值和方差来估计全部待测电路的木马比例因子的差异,实现对HT的检测。表6中,文献[15]设定时钟树区域为公共区域,与每个区域合并后对比例因子进行求解,利用公共区域的比例因子进行比较判断HT,但需要限制未植入HT时的钟树区域,这是由于当HT植入时钟树公共区域的情况下,合并后的每个区域将都存在HT,求解的比例因子都会异常,需要重新对HT进行评判。而本文方法是直接对电路进行分区,根据每个分区的木马比例因子差异识别HT,简单实用、通用性更好。本文方法可检测木马占比高于0.04%,可以实现HT区域定位。

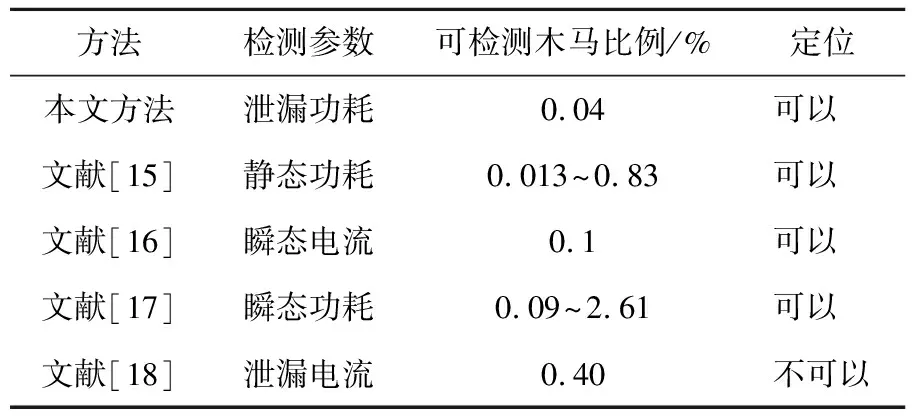
表6 不同木马检测方法比较

5 结 论

为改进基于GLC的HT检测能力与效率,本文提出了一种基于电路分区自比较的HT检测方法。直接将电路进行分区,然后对区域电路的泄漏功耗进行门级特性仿真,并通过线性回归算法求解得到每个区域的木马比例因子,最后通过比较区域电路木马比例因子异常性,判断HT的存在并定位其所在区域。本文方法无需引入获取困难的黄金模型,无需触发HT活性,可以检测规模占待测电路0.04%以上的微小型HT。未来工作将进一步研究探讨电路划分数量与检测能力的具体依赖性,研究如何通过门组的概念引入以减少检测时间。