逼近离散序列的多项式拟合模型的方法分析研究

杨 鑫，蔺 琳

(大连财经学院，辽宁 大连 116000)

0 引言

在实验和统计中，需要根据已知的离散数据序列，采用函数逼近方法，构造与该序列误差较小的函数，可以通过观察和测试获得f(x)的一组离散的数据[1].当获得的实验数据是足够准确的，可以利用代数插值法进行计算从而近似原始函数.当实验数据的观察或测量不够准确，插值法误差则较大，可以使用最小二乘法进行函数逼近，降低误差，效果较好.尽管求出的逼近曲线不一定经过所有点,但是会最大可能的接近原始曲线[2].函数逼近的数值方法从实际应用的角度来看，要解决一个函数的最佳逼近问题，需要构造出最佳逼近元和算出最佳逼近值[3].一般说要精确解决这两个问题十分困难.这种情况要寻求最佳逼近元的近似表示和最佳逼近值的近似估计而设计出各种数值方法[4].本文针对离散的数据序列，采用函数逼近的方法，构造与该数据序列误差较小的函数，具体包括多项式最小二乘法拟合，正交多项式最小二乘法拟合，并在Matlab中进行有关曲线拟合仿真实验.

1 数据拟合与函数逼近相关理论概述

1.1 曲线拟合的最小二乘法理论

假定有一组数据(xi,yi)，人们都希望可以找到近似函数，它在反映已知数据的变化趋势的基础上，产生的误差不是很大，而且让获得的近似函数和被逼近的函数在一个给出的区间内产生误差满足相关的要求，这就是曲线拟合的思想[5].

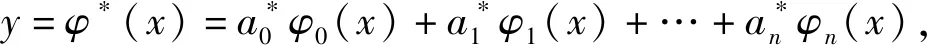
(1)

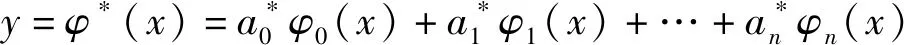
最小二乘法在Matlab的环境下,提供了很多的好方法进行拟合.不仅可以利用函数的方法进行拟合,而且可以利用图形界面拟合和曲线拟合工具箱拟合.

1)函数Polyfit进行多项式拟合

选择合适的数学拟合公式是非常重要的，在进行数据拟合时，可以利用Matlab本身提供的函数进行线性曲线拟合[8].Polyfit函数的调用方式为p=polyfit(x,y,m),多项式曲线拟合是较频繁使用的拟合数据的方式.如果数据比较多，多项式的阶数一般很低，拟合的精确程度和实验的效果都不太好.要提高拟合的精确程度和效率就要增大曲线的阶数，计算上的复杂性及其他方面的不利又来源于阶数较高.因此，拟合很多的数据仅仅只使用一种多项式曲线函数，又很不容易获得高效率、高精度，利用分段的曲线拟合可以解决问题.

2)利用函数lsqcurvefit进行非线性函数拟合

对于非线性拟合，除少数形式外，大多数条件下是不能化成线性拟合，需要用非线性最小二乘法直接求解.该函数的调用格式为x=lsqcurvefit(y,x0,xd,yd)，y为非线性函数，x0为初始参数，xd,yd是要拟合的数据.

1.2 多项式拟合原理

若拟合模型p(x)=a0+a1x+…+anxn则称其为多项式拟合.由最小二乘法确定系数a0,a1,…,an假设各点权为1，考虑

(2)

令其值最小，则有

(3)

(4)

此方程组为多项式拟合的法方程.

(5)

XY=A，A=X-1Y通过矩阵方程，得到拟合多项式的系数；即p(x,A)=a0+a1x+…+anxn;当拟合次数n比较大的情况下，方程的系数矩阵就变得病态，获取的结果误差很大，导致实验结果没有意义.因此，在实际进行多项式曲线拟合时，拟合次数不适合取值很大.当拟合次数为零时，得到一种简单的拟合模型p(x)=a0+a1x，这种模型计算比较简单，被普遍地使用.

1.3 正交多项式最小二乘法拟合原理

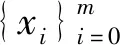
(6)

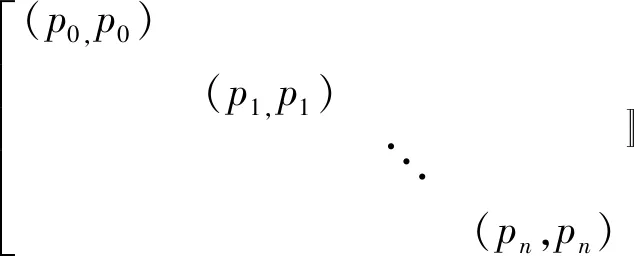
(7)

于是在正交多项式p(x)下的多项式拟合为

(8)

在给定结点xi(i=0,1,…,m)的情况下,可以用递推公式的导出pi(x).设

(9)

这里pi(x)是首项系数为1的i次多项式.由正交性可得

(10)

图1 数据拟合结果

2 结果分析

2.1 曲线拟合结果分析

本文以某种食品每件平均单价y与批量x之间的关系为样本进行了数据拟合仿真实验，其中x=[20 25 30 35 40 50 60 65 75 80]，y=[1.81 1.70 1.65 1.55 1.48 1.40 1.30 1.25 1.21 1.20]，其数据分布如图1所示.分别利用二次多项式和正交多项式(最小二乘法)对数据进行拟合，拟合后得到二次多项式的模型为y=0.000 1x2-0.023 2x+2.213 1，正交二次多项式的模型为y=0.000 1x2-0.023 1x+2.208 3，拟合曲线结果见图1.

从图1可以看出，二次多项式拟合和正交多项式拟合都可以得到拟合曲线，并且两种方法得到的曲线基本重合.

2.2 误差分析结果

为了剖析不同拟合次数对两种拟合方法的影响，对数据分别进行9次拟合，观察其拟合后每个x值对应的y值的误差平方和，结果见表1.

表1 不同拟合次数对拟合结果误差平方和的影响

由表1可得，在多项式拟合结果中，拟合次数小于7时拟合次数越高，拟合结果的y值与实际数据的误差越小，曲线越来越接近原始数据，曲线越逼近实际情况，实验结果越精确.而正交多项式的拟合结果显示，在拟合次数为5时拟合结果的误差平方和达到最小，与真实结果最接近.为了直观了解各个点实验值的误差分布情况，通过Matlab调用函数lsqcurvefit获取拟合的曲线，得到拟合后方程的系数p分布情况，见图2.

图2 不同拟合次数对拟合方程系数的影响

由图2可看出利用多项式拟合，如果拟合次数大于或等于7，与利用正交多项式最小二乘法拟合相比，拟合次数增高，求出方程系数增加程度较小，求出方程解误差增大.因此，在求解离散数据系列中如要求拟合次数较多，应选择正交多项式作最小二乘法曲线拟合.

综上所述，多项式拟合的优点是简单方便.但其最大缺点为如果拟合次数高于或者等于7次，经过计算和分析，多项式拟合所得的正规方程组通常是病态的，会产生较大误差，因此应选用正交多项式方法求解.使用最小二乘法进行曲线拟合时，可以通过拟合后每个点的y值与实际y值相比较进行误差分析，也可用误差平方和极小作为拟合标准，误差平方和能在整体水平上系统地评价拟合后的精确度.对于拟合次数较高的，也要选用正交多项式进行拟合，得出的结果会更精确.对于曲线拟合，拟合次数越多，正交多项式最小二乘法的实验结果的曲线越发接近原始数据，实验结果越准确，误差越小.

3 结语

在实验中，利用了多项式最小二乘法，正交多项式最小二乘法.同时，通过Matlab拟合工具箱调用相应的函数进行非线性函数拟合，进行误差分析，并且选择最适合的最小二乘法进行拟合.结果表明，基于最小二乘法原理的曲线拟合能够清晰地表现出变量间的函数关系，还能通过数据点与曲线的偏离程度大致估计观测误差.正交多项式拟合比多项式拟合具有更小的拟合误差，能够提高实验结果的精确性.