嵌入空间的低秩张量填充算法

杨庆圆,王川龙

(太原师范学院 工程科学计算实验室/数学与统计学院,山西 晋中 030619)

0 引言

随着信息技术的迅猛发展，存储和处理数据已经成为至关重要的问题，且真实数据都具有结构复杂和大规模的特点，如彩色图像、视频序列等，通常用张量来表示.张量填充是张量分析和处理中的一个重要问题，深受专家和学者的关注.它主要应用于如数据挖掘[1]、机器学习[2]、图像处理[3]、医学影像[4]等领域.张量填充问题的优化模型如下：

s.t.PΩ(X)=PΩ(T)

(1)

其中X∈I1×I2×…×IN是N阶填充张量，T∈I1×I2×…×IN是N阶观测张量，rank(X)代表张量的秩，且有多种定义，如CP秩，Tucker秩，Tubal秩，TT秩，TR秩等.PΩ是集合Ω上的正交投影算子，即：

与矩阵类似,张量秩函数的计算同样是NP-hard的.张量核范数首先由Liu等人[5,6]于2009年提出，基于最小化Tucker秩将模型(1)凸松弛为：

s.t.PΩ(X)=PΩ(T),i=1,2,…,N

(2)

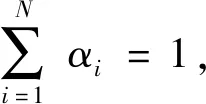
针对张量正向切片中行和列的缺失，研究此类结构缺失的低秩张量填充问题，基于高精度低秩张量填充算法的模型，引入延迟嵌入的思想，提出相应算法，对彩色图像进行填充实验，验证了所提出算法的有效性.

文章结构如下：第1节介绍张量、矩阵的基础知识；第2节介绍高精度低秩张量填充算法(HaLRTC)和多向延迟嵌入变换(MDT)[14,15]；第3节提出了嵌入空间中的低秩张量填充算法(MDT-LRTC)；第4节利用Matlab进行数值和彩色图像实验，并与HaLRTC、DR-TR这两种算法进行了比较，验证了所提算法的有效性；第5节是总结部分.

1 符号说明及定义

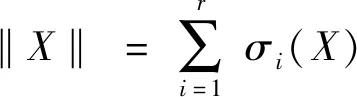
定义1(奇异值分解[16]) 设X∈I1×I2是一个秩为r的矩阵，则必存在正交矩阵U∈n1×r和V∈n2×r，满足：

X=UΣrVT，∑r=diag(σ1,…,σr)，

其中σ1≥σ2≥…≥σr≥0.

定义2(奇异值阈值算子[17]) 对于任意参数τ≥0，矩阵X∈I1×I2的秩为r，则存在X=UΣrVT，奇异值阈值算子Dτ定义为：

Dτ(X)=UDτ(Σ)VT，Dτ(Σ)=diag({σk-τ}+)，

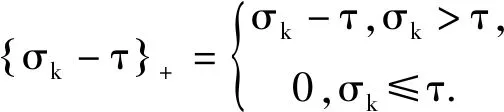
定义3(广义逆[18]) 对于任意的矩阵X∈I1×I2，若存在某个矩阵G∈I2×I1，满足以下四个方程，则称G为X的广义逆矩阵，X+=(XTX)-1XT为广义逆(本文将广义逆称之为伪逆).

XGX=X；GXG=G；(XG)T=XG；(GX)T=GX.

定义4(张量的n模态矩阵积[19])N阶张量X∈I1×I2×…×IN与矩阵U∈J×In的n模态矩阵积是一个维度为I1×…×In-1×J×In+1×…×IN的张量，表示为X×nU，且有如下元素对应关系：

2 相关算法

2.1 高精度低秩张量填充算法(HaLRTC)

2013年Liu等人[6]结合交替方向乘子法，引入中间变量Mi，将模型(2)转化为如下问题：

s.t.PΩ(X)=PΩ(T)

X=Mi,i=1,…,N

(3)

算法1高精度低秩张量填充算法(HaLRTC)

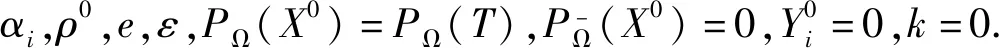
输出：填充张量X.

第1步：fori=1:N

end

第3步：若‖Xk+1-Xk‖F/‖Xk‖F<ε，停止迭代，否则转第4步；

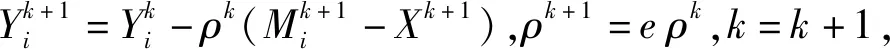
2.2 多向延迟嵌入变换(MDT)

为简单起见，先定义向量的标准延迟嵌入变换.假设向量v=(v1,v2,…,vL)T∈L，延迟嵌入变换的参数为τ，则v对应的标准延迟嵌入变换Hτ(v)为：

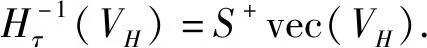
(a)标准延迟嵌入的正向变换

(b)复制矩阵

(c)逆变换

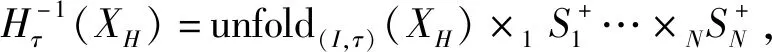
3 新算法

实际生活中收集到的数据往往由于设备或传输等问题导致数据缺失，如图片和视频数据在传输过程中可能会出现整行整列缺失的情况；医学图像如核磁共振影像可能会由于病人的身体晃动或漏做某项检查出现条状或块状缺失的情况等.针对这个问题，提出了如下算法，可以有效的填充这种结构缺失的数据.

算法2嵌入空间中的低秩张量填充算法(MDT-LRTC)

输入：原始张量T，采样集合Ω，采样张量PΩ(T)，向量τ，参数αi，ρ0，e，ε.

输出：最终的填充张量X.

第1步：构造复制矩阵S，利用多向延迟嵌入变换(MDT)将N阶张量T和X以及采样算子PΩ变为2N阶Hankel张量H(T)、H(X)和PΩ；

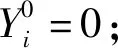
第3步：fori=1:2N

end

第5步：若‖(H(X))k+1-(H(X))k‖F/‖(H(X))k‖F<ε，停止迭代，否则转第6步；

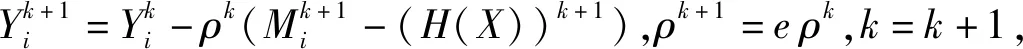
第7步：利用逆多向延迟嵌入变换(逆MDT)将得到的2N阶张量H(X)变为最终的N阶填充张量X.

4 实验结果

采用大小为256×256×3的peppers(1)https:∥ccia.ugr.es/cvg/dbimagenes/彩色图像，分别用MDT-LRTC算法与HaLRTC、DR-TR算法进行采样填充，从相对误差(RSE)、峰值信噪比(PSNR)、结构相似度(SSIM)三个方面验证新算法的性能.所有的数值代码都是用Matlab(R2019b)编写，数值实验都是在戴尔(DELL) PowerEdge R740xd高性能2U机架式并行运算服务器上实现的.

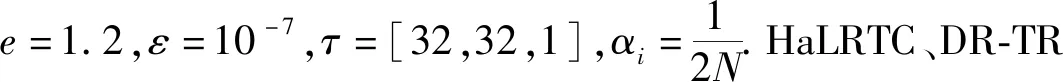
SSIM(Xhat，T)=[l(Xhat，T)αc(Xhat，T)βs(Xhat，T)γ]，

其中l(Xhat，T)、c(Xhat，T)、s(Xhat，T)分别表示亮度比较函数、对比度比较函数和结构相似度比较函数，α，β，γ分别为上述三个函数这三个分量的相对重要性.

图1 只对张量的每个正向切片的行和列采样的填充效果

表1 只对张量的每个正向切片的行和列采样的数值结果

由图2可知，新算法MDT-LRTC相较于HaLRTC、DR-TR算法来说，不仅可以恢复随机缺失的图像，而且对于有结构缺失的图像恢复效果也很不错.

由表2可知，新算法MDT-LRTC的相对误差更小，峰值信噪比和结构相似度更高，有力说明新算法的高效性能.

图2 随机采样并对张量正向切片的行和列采样的填充效果

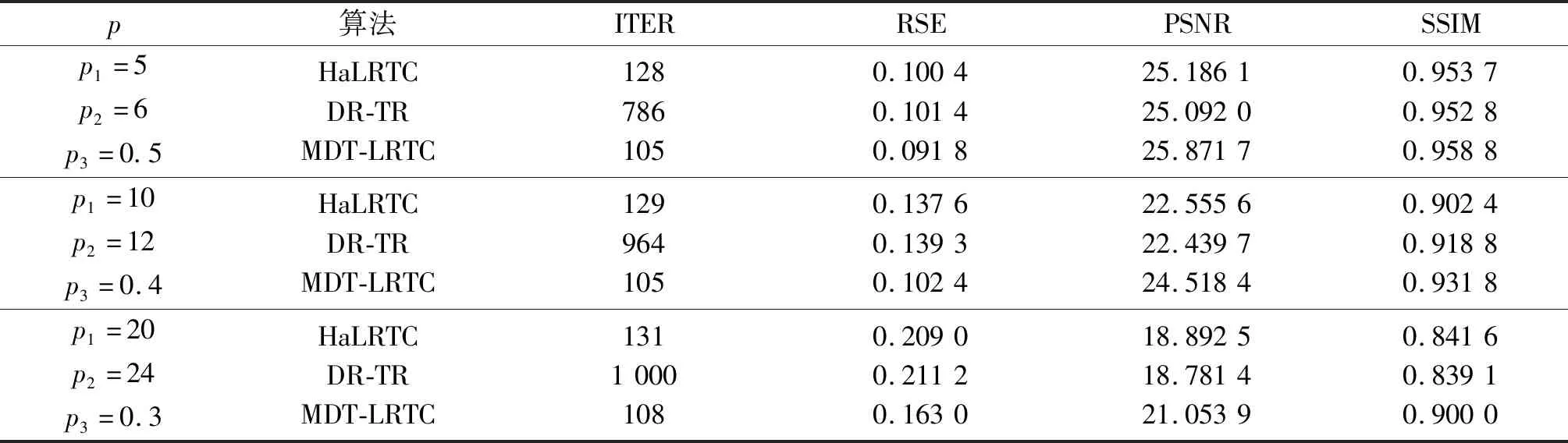
表2 随机采样并对张量正向切片的行和列采样的数值结果

5 总结

提出了基于多向延迟嵌入低秩张量填充算法，在原有的高精度低秩张量填充算法的基础上，结合数据的条状或块状这种结构缺失，引入了嵌入空间的思想，对多向延迟嵌入变换得到的高阶Hankel张量进行填充.由图和表均可以看出，针对彩色图像填充，新算法占有很大优势.