通过1-2最小化恢复信号的充分条件

武思琪,宋儒瑛

(太原师范学院 数学与统计学院，山西 晋中 030619)

0 引言

(1)

其中‖x‖0:=|supp(x)|，其中supp(x)={i:xi≠0}表示x的支撑集或简称为支撑；|supp(x)|表示supp(x)的基数，也就是集合supp(x)中元素的个数.式(1)是最直接的稀疏信号重建方法，但这是一个NP-难问题，计算上是不可行的，因此Candes和Tao[1]想到用1范数对其松弛，即转化为求解1最小化问题，这将求解0最小化所涉及的多个子问题的优化问题转化为凸优化问题，从而更容易求解，但其需要更多的测量值.近年来，Yin等人[2]提出了用下面的1-2最小化问题来代替式(1)：

(2)

他们证明了当测量矩阵A满足良好的限制等距性时，式(2)也可以稳定和鲁棒地恢复稀疏信号，且1-2最小化方法的性能优于包括1最小化方法在内现存的其他方法[3,4].

压缩感知中使用最多的是满足限制等距性(RIP)的框架，它刻画了一个矩阵和标准正交矩阵的相似程度.研究证明[5]如果一个矩阵A满足RIP，那么这就足以使各种算法能够成功地从噪声测量值中恢复稀疏信号.另一个广泛使用的框架是零空间特性，人们通常利用测量矩阵的零空间特性来建立基于限制等距性的充分条件，从而精确恢复稀疏信号[6,7].在实际应用中，信号恢复通常会利用自身的先验支撑信息来提高信号恢复的效率，文献已经证明了在1-2[3,8]、1[9,10]、p(0

1 预备知识

首先引入一些定义[5,8]和引理[5,8]来为文章的主要结果作铺垫.

定义1[5]对所有h-稀疏信号x∈n(即至多有h个非零项)，若存在一个最小的常数δh∈(0,1)，使得

(3)

定义2[8]对所有集合S⊆{1,…,n}(|S|≤h)，若对任意x∈N(A)(N(A)是A的零空间)，且x≠0，使得

‖xS‖1+‖x‖2<‖xSc‖1

(4)

定义3[8]对所有集合T⊆{1,…,n}(0≤|T|=k

‖xS‖1+‖xTc‖2<‖x(S∪T)c‖1

(5)

注:当k=0，即T=∅时，定义3是1-2零空间特性.

在更现实的情形中，信号x不是完全稀疏的，但它是一个可压缩信号(可以由一个稀疏信号很好地逼近).在这种情形中，我们引入部分支集已知的1-2稳定零空间特性的定义.

定义4[8]对所有集合T⊆{1,…,n}(0≤|T|=k

‖xS‖1+‖xTc‖2≤μ‖x(S∪T)c‖1

(6)

成立，其中0<μ<1，则称矩阵A∈m×n满足部分支集已知的h阶的1-2稳定零空间特性(T是已知支撑集).

引理1[5]对向量x,r∈n，其中‖x‖0≤w且‖r‖0≤t，A∈m×n.若supp(x)∩supp(r)=∅，且存在常数δw+t，满足

|〈Αx,Αr〉|≤δw+t‖x‖2‖r‖2,

(7)

则称δw+t是w+t阶的限制等距常数.

引理2[5]给定q>p>0，对向量x,r∈n，其中‖x‖0≤w且‖r‖0≤t，且supp(x)∩supp(r)=∅，满足

则

(8)

引理3[8]令k是一个给定的正整数，x是一个给定的信号，满足|supp(x)|≤h.假设矩阵A满足部分支集已知的h阶的1-2零空间特性，则x是式(2)的唯一解.

引理4[8]当k=0，即T=∅，x是一个给定的信号，满足|supp(x)|≤h.假设矩阵A满足h阶的1-2零空间特性，则x是式(2)的唯一解.

备注1[8]由于‖xS‖1+‖xTc‖2≤μ‖x(S∪T)c‖1<‖x(S∪T)c‖1，假设矩阵A满足部分支集已知的h阶的1-2稳定零空间特性，则x是式(2)的唯一解.

2 主要结果

若信号是完全稀疏的，则通过式(2)可以精确恢复稀疏信号；若信号是不完全稀疏，而是一个可压缩信号(可以由一个稀疏信号很好地逼近)，则通过式(2)可以稳定恢复信号.

下面给出本文的三个主要定理，分别适用于一般信号精确恢复、具有部分先验支撑信息的信号精确恢复及具有部分先验支撑信息的信号稳定恢复.

定理1假设矩阵A∈m×n的2h阶限制等距常数满足

(9)

则每个h-稀疏向量x∈n是

的唯一解.

证明 根据定义2，对所有g:=v-x∈N(A)和S⊂{1,…,n}(card(S)=h)，可以建立如下不等式：

(10)

为了说明式(10)，由式(4)得到

‖gS‖1+‖g‖2<‖gSc‖1⟹

‖gS‖1+‖gS‖1+‖g‖2<‖g‖1⟹

2‖gS‖1+‖gS‖2+‖gSc‖2<‖g‖1⟹

这遵从更强的条件：

其中

给定g∈N(A)，考虑向量g的h个最大绝对值项的一个指标集S:=S0.现将集合{1,…,n}中S0的补集S0c划分为S0c=S1∪S2∪…，其中

S1：S0c中g的h个最大绝对值项的指标集；

S2：(S0∪S1)c中g的h个最大绝对值项的指标集；

⋮

由于g∈N(A)，有Α(gS0)=Α(-gS1-gS2-…)，使得

(11)

根据引理1，得到

|〈Α(gS0),Α(-gSi)〉|≤δ2h‖gS0‖2‖gSi‖2.

(12)

由于‖gS0‖2>0，现在将式(11)和式(12)结合起来，且两边同时除以‖gS0‖2，得到

对于i≥1，gSi的h个绝对值项的大小不超过gSi-1的h个绝对值项的大小，所以由引理2可以推导出

从而得到

由引理4得证.

定理2假设矩阵A∈m×n的2h+k阶限制等距常数满足

(13)

则每个具有部分已知支撑集T的h-稀疏向量x∈n(card(T)=k

的唯一解.

证明 根据定义3，对所有g:=v-x∈N(A)和S⊂{1,…,n}(card(S)=h)，可以建立如下不等式：

(14)

为了说明式(14)，由式(5)得到

‖gS‖1+‖gTc‖2<‖g(S∪T)c‖1⟹

‖gS‖1+‖gTc‖2+‖gS∪T‖1<‖g‖1⟹

这遵从更强的条件：

和

T⊂{1,…,n}(card(S)=h,card(T)=k)，

其中

给定g∈N(A)，T为向量g的部分已知支撑集.现将集合{1,…,n}中T的补集Tc划分为Tc=T0∪T1∪…，其中

T0：Tc中g的h个最大绝对值项的指标集；

T1：(T∪T0)c中g的h个最大绝对值项的指标集；

⋮

(15)

根据引理1，得到

(16)

对于i≥1，gTj的h个绝对值项的大小不超过gTj-1的h个绝对值项的大小，所以由引理2推导出

从而推出

由引理3得证.

定理3假设矩阵A∈m×n的2h+k阶限制等距常数满足

(17)

则每个具有部分已知支撑集T的h-稀疏向量x∈n(card(T)=k

稳定恢复.

证明 根据定义4，对所有g:=v-x∈N(A)和S⊂{1,…,n}(card(S)=h)，可以建立如下不等式：

(18)

为了说明式(18)，由式(6)得到

‖gS‖1+‖gTc‖2≤μ‖g(S∪T)c‖1⟹

‖gS‖1+‖gTc‖2+μ‖gS∪T‖1≤μ‖g‖1⟹

其中0<μ<1.

这遵从更强的条件：

和

T⊂{1,…,n}(card(S)=h,card(T)=k)，

其中

接下来的证明过程依照定理2和备注1即可得证.

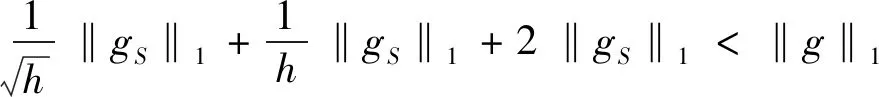
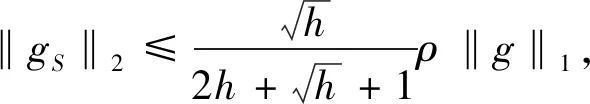
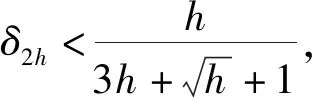
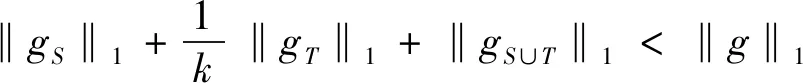
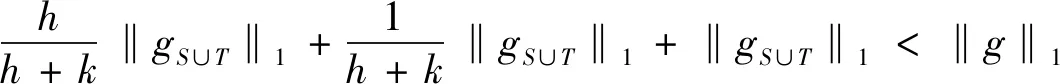
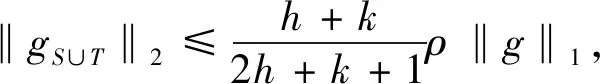
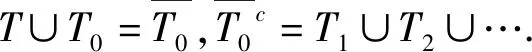
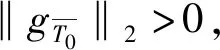
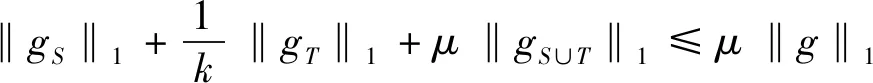
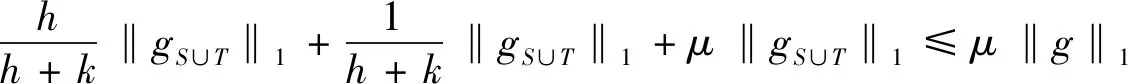
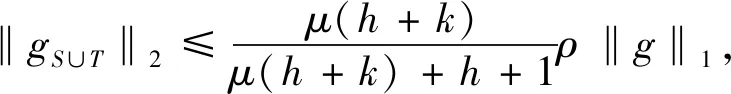
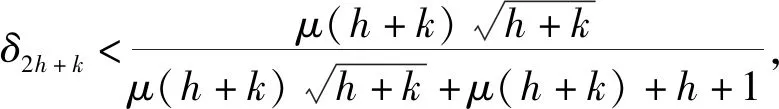
3 结论