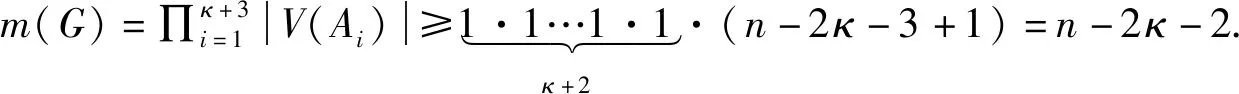基于最大独立集个数下的至多3个叶子点支撑树的存在性
2023-01-05雷万鹏李瑞霖
雷万鹏,李 婷,李瑞霖
(1.太原师范学院 数学与统计学院,山西 晋中 030619;2.山西工程科技职业大学 基础教学部,山西 晋中 030619)
1972年,Chvátal和Erdös[1]利用独立数和连通度给出了图是哈密尔顿的(可迹的,哈密尔顿连通的)一个著名的充分条件.用κ(G)和α(G)分别表示图G的连通度和独立数.
定理1(Chvátal和Erdös)[1]如果G是顶点个数至少是3的简单图,并且满足α(G)≤κ(G)(α(G)≤κ(G)+1,α(G)≤κ(G)-1),那么G是哈密尔顿的(可迹的,哈密尔顿连通的).
定理1被延拓至许多不同的方向[2-8].
哈密顿路可以看作是恰好有两个叶子点的支撑树.从这个角度上看,一些图可迹的充分条件可以拓展到至多k个叶子点的支撑树存在的充分条件.很显然,如果s≤t,那么一个至多s个叶子点的支撑树也是至多t个叶子的支撑树.Win将定理1推广到至多k个叶子点的支撑树上.
定理2(Win)[9]令k≥2且G是连通简单图.如果α(G)≤κ(G)+k-1,那么G中有一个至多k个叶子点的支撑树.
从一般意义上来讲,独立数反映了图的稀疏程度,而连通度反映了图的密集程度.而实际上,独立数作为图的一个参数,并不能反映图在整体意义上的稀疏程度,它只是一个图的局部范围内的指标.为了能更准确地反映图的稀疏程度,Chen[10]等引入了最大独立集个数这个指标,令m(H)为图G的子图H的最大独立集的个数.并且证明了当限制m(H)的范围时,G的独立数稍微扩大一点(即α(G)≤κ(G)+2)不会改变其可迹性.
定理3(Chen等)[10]设G为n≥2κ2(G)的2-连通图.如果κ(G)=κ,α(G)≤κ+2.并且m(G)≤n-2κ-1,那么要么G是可迹的,要么G属于某一类反例图.
Lei等[11]将Chen等的结论拓展到了至多k个叶子点的支撑树上,Lei等推广了Win定理并得到以下结果.
定理4(Lei等)[11]令k≥2且G是一个n≥2k+2的连通简单图.如果α(G)≤1+k并且m(G)≤n-2k-2,那么G中有至多k个叶子点的支撑树.
然而,定理4中m(G)的界并不是紧的.本文主要研究了基于最大独立集个数的至多3个叶子点支撑树的存在性问题,并得到了m(G)的界是最好可能的.为了证明主要结论,利用如下引理.
引理5[11]假设X是G中最大的一个独立集.令S⊂V(G)使得|S∩X|=1,设{z}=S∩X.如果对任意的x∈
假设S是G中一个子图,令c(G-S)为G-S的分支个数.下面是本文主要结论:
定理6令G是一个简单图,P是G中一条最长路.如果α(G)≤κ(G)+3,c(G-P)≥2,m(G)≤n-2κ(G)-3并且G-P的每一个分支在P中邻点相同,那么G中包含一个至多3个叶子点的支撑树.
注:由定理2可知,定理4中图G的连通度为1.由此可见,本文结论中最大独立集的个数的界比定理4中的界要好,并且是最好可能的,对于连通度也没有任何限制.
1 符号与术语
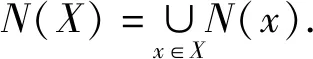

2 定理6的证明
证明 假设G中不包含一个至多3个叶子点的支撑树,则G中没有哈密尔顿路,故P不是哈密尔顿路.令aP和bP为P的两个端点.对P从aP到bP定向,因此,对于V(P)中的每一个内部顶点x,定义x+,x-.对于P中任给的顶点x,y,P[x,y]指由P中连续顶点构成的一条路xx+x2+…xs+(=y).

因为P是G中的一条最长路,所以很容易验证aP,bP∉U,并且下列{ν,aP}∪U+和{ν,bP}∪U-是G中的两个独立集.又因为c(G-P)≥2,不妨令ν∈V(D1),ω∈V(D2),D1,D2分别为G-P的两个不同的分支.
则{ν,ω,aP}∪U+和{ν,ω,bP}∪U-是独立数为κ+3的G中的两个独立集.令X={ν,ω,aP}∪U+,Y={ν,ω,bP}∪U-,则c(G-P)=2,否则与独立数κ+3矛盾.
断言1D1,D2都是一个团.
证明 由对称性,只考虑D1即可.由分支的定义,仅考虑|V(D1)|>2.假设任意取两点v1,v2∈V(D1)且v1v2∉E(G).
如果viaP∈E(G)(i=1,2),那么viP是一条比P长的路,与P是G中最长路相矛盾.故viaP∉E(G)(i=1,2),同理vibP∉E(G)(i=1,2).

如果v1v2∉E(G),{ω,v1,v2,aP}∪U+是G中的独立集,则独立数为κ(G)+4与κ(G)+3矛盾,故v1v2∈E(G),由v1,v2∈V(D1)的任意性,D1是团.证毕.

图1


图2

图3
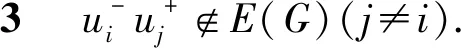
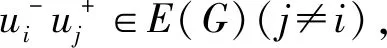

图4

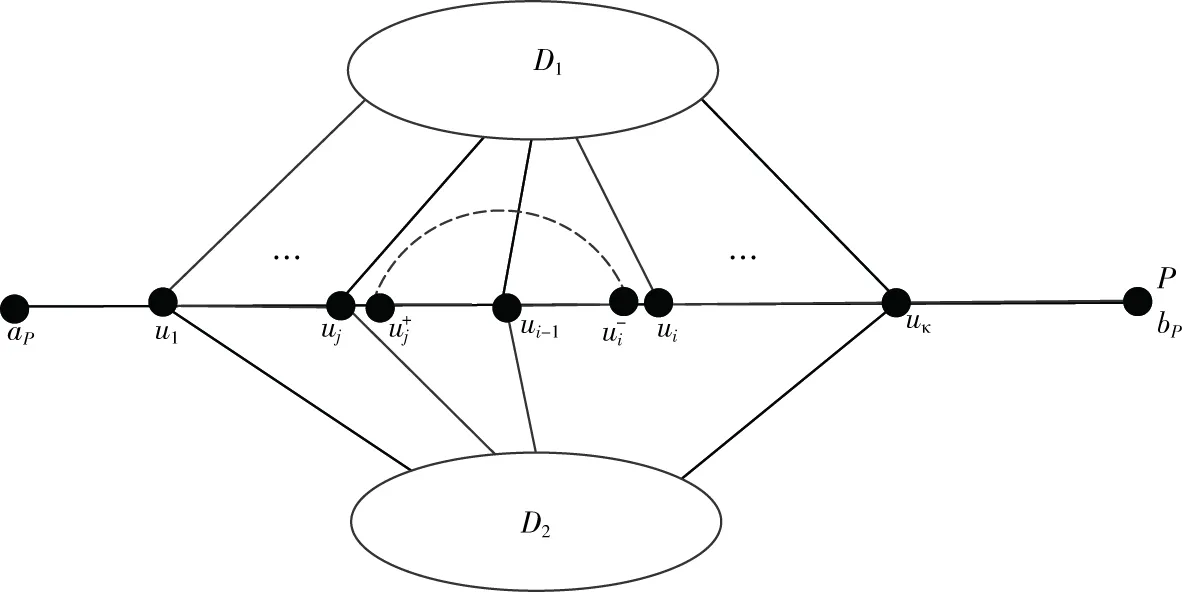
图5
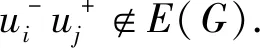
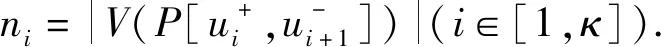
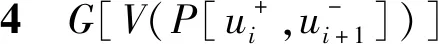
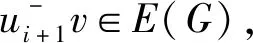
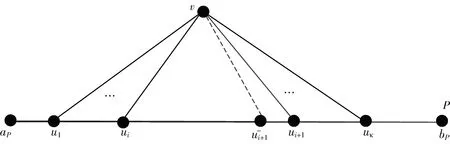
图6
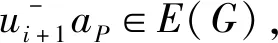

图7
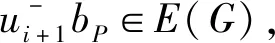

图8
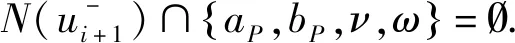


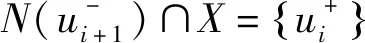



图9

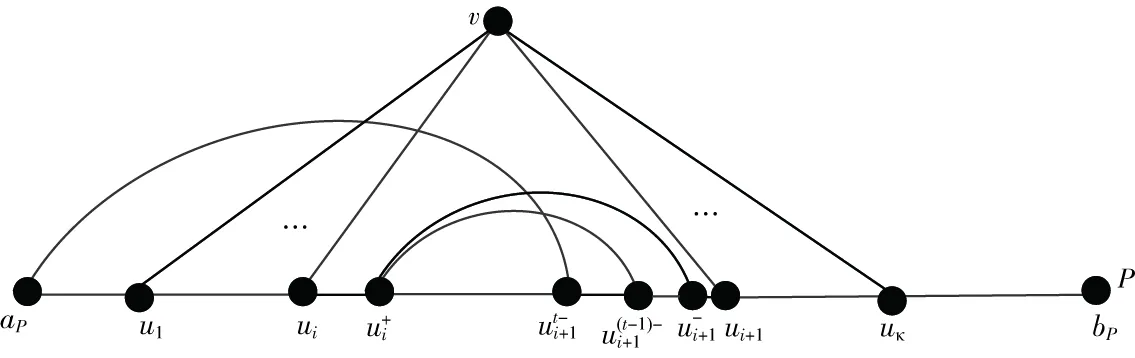
图10
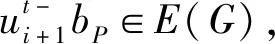

图11


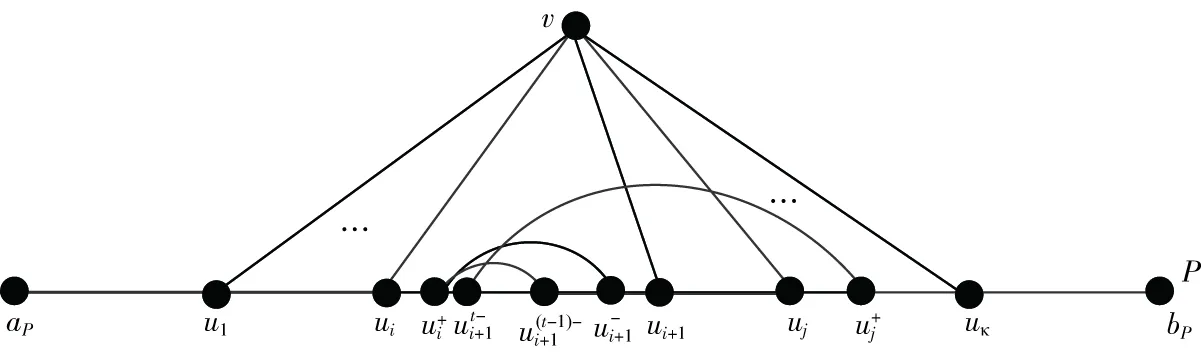
图12
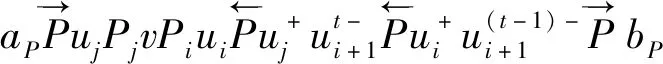

图13
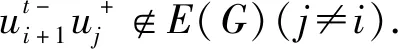

由断言1,2和4,很容易验证:
断言5c(G-U)=κ+3,即任意两个团Ai均互不相邻.