基于矢量分解和双随机相位编码的图像加密系统

2023-01-05窦帅风马静

光散射学报 2022年3期

窦帅风，马静

(中国人民解放军61932部队，北京 100166)

1 引言

随着技术的发展，当今社会所需处理的信息量呈爆炸式增长。光学加密作为光学信息处理的一部分，以其多维加密自由度和高速并行处理等优势，受到了广泛关注。自从双随机相位编码(double random phase encoding, DRPE)方法[1]被提出以来，研究者对光学加密进行了深入的研究，多种光学加密方法被提出，如基于联合变换相关器的加密系统[2]、非对称加密系统[3]、基于衍射成像的加密系统[4]、非相干加密系统[5]及基于相移干涉的加密系统[6]等。

双随机相位编码作为具有代表性的一种光学加密方法，其基于4-f系统，通过使用两个随机相位模板，能够将原始图像加密为白噪声密文。研究者对双随机相位编码加密系统的特性进行了研究[7-10]，并将双随机相位编码从傅里叶域拓展至分数阶傅里叶域[11,12]、菲涅耳域[13,14]及Gyrator域[15]。在双随机相位编码的基础上，结合数字全息、压缩感知、信息隐藏等其它相关技术，新的加密方法也被提出[16-26]。

随着对光学加密的研究，一些针对光学加密的攻击方法也被提出，例如唯密文攻击[27,28]、已知明文攻击[29]和选择明文攻击[30,31]等，攻击者通过这些方法可以获得原始图像或密钥等信息。为了增强加密系统的安全性，文献[32]使用相位恢复算法，并使用指纹作为密钥，对图像进行加密；文献[33]利用混沌映射以增强系统的安全性；文献[34]利用振幅和相位截断，提出了一种非对称加密系统。

本文基于矢量分解和双随机相位编码，设计了一种光学加密系统，通过矢量分解增加了一个密钥，拓展了系统的密钥空间。加密系统具有较好的加密和解密效果，并具有较高的安全性。

2 图像加密及解密原理

2.1 矢量分解

令g(x,y)表示归一化的原始图像，通过矢量分解可将原始图像g(x,y)在复平面上分解为两个相位模板g1(x,y)和g2(x,y)。如图1所示，Re和Im分别表示实部和虚部，虚线圆表示单位圆，且

图1 矢量分解示意图

(1)

其中r(x,y)是[0,1)区间中均匀分布的随机序列，即g2(x,y)是随机相位模板。令

α(x,y)=2arccos[g1/2(x,y)],

(2)

则

|U(x,y)|2=|g1(x,y)+g2(x,y)|2=4g(x,y),

(3)

即

g(x,y)=|g1(x,y)+g2(x,y)|2/4,

(4)

2.2 图像加密

图像加密系统如图2所示，与双随机相位编码不同的是，待加密图像是矢量分解得到的相位模板g1(x,y)，而非原始图像g(x,y)。相位模板g1(x,y)位于透镜L1的前焦面x-y上，随机相位模板k(x1,y1)作为密钥模板位于透镜L1的后焦面x1-y1上。当入射光波是波长为λ的单色平面波时，在透镜L2的后焦面可得到密文

图2 图像加密系统示意图

e(x,y)=IF{F{g1(x,y)}k(x1,y1)},

(5)

其中F{⋅}和IF{⋅}分别表示傅里叶变换及逆傅里叶变换。

2.3 图像解密

图像解密系统如图3所示，解密时需同时拥有密钥k(x1,y1)和密钥g2(x,y)。密文e(x,y)位于透镜L1的前焦面x-y上，解密密钥k*(x1,y1)是加密密钥k(x1,y1)的共轭相位模板，并位于透镜L1的后焦面x1-y1上。在波长为λ的单色平面波的照射下，在透镜L2的后焦面x-y上，可得到解密光束的复振幅分布为

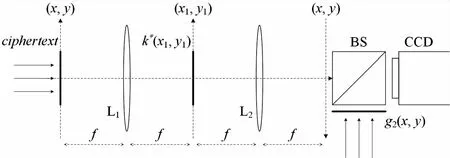
图3 图像解密系统示意图(BS, 分光棱镜)

o(x,y)=IF{F{e(x,y)}k*(x,y)}

=g1(x,y),

(6)

其中上标*表示共轭。

解密光束o(x,y)通过分光棱镜BS后，与经密钥模板g2(x,y)调制的光束相干叠加，所得光场的强度分布可用CCD相机记录，即

=4g(x,y),

(7)

也就是解密得到的原始图像g(x,y)。

3 数值模拟分析

3.1 加密及解密效果

为验证加密系统的加密及解密效果，对图4(a)所示的原始图像g(x,y)进行加密，原始图像的尺寸为400×400像素。通过矢量分解可将g(x,y)分解为相位模板g1(x,y)和密钥相位模板g2(x,y)，分别如图4(b)和图4(c)所示。另一密钥相位模板k(x1,y1)如图4(d)所示。通过加密系统得到的密文e(x,y)如图5(a)所示，可以看出密文呈噪声状，成功实现了图像加密。当使用k(x1,y1)的共轭相位模板k*(x1,y1)及密钥模板g2(x,y)对密文进行解密时，所得解密图像如图5(b)所示，可以看出成功地恢复出了原始图像。

用相关系数(correlation coefficient)CC定量评价图像解密效果，

(8)

其中g′表示解密图像，g表示原始图像，(i,j)表示图像像素的坐标。CC表示解密图像与原始图像之间的相似程度，其值越接近1，图像解密效果越好。计算图5(b)所示的解密图像与图4(a)所示的原始图像之间的相关系数得到CC=1.0，系统具有较好的解密效果。

图4 原始图像及密钥模板。(a)原始图像g(x,y);(b)相位模板g1(x,y);(c)密钥相位模板g2(x,y);(d)密钥相位模板k(x1,y1)

相较于双随机相位编码系统，文中加密系统通过矢量分解增加了一个密钥相位模板g2(x,y)。解密过程中，密钥模板k(x1,y1)或g2(x,y)错误时，系统的解密效果如图6所示，图6(a)和图6(b)是两个随机生成的相位模板，分别表示错误密钥k′(x1,y1)和错误密钥g2′(x,y)。当使用错误密钥k′(x1,y1)和正确密钥g2(x,y)对图5(a)中的密文解密时，解密图像如图6(c)所示；当使用正确密钥k(x1,y1)和错误密钥g2′(x,y)解密时，解密图像如图6(d)所示；当使用错误密钥k′(x1,y1)和错误密钥g2′(x,y)解密时，解密图像如图6(e)所示。可以看出，图6(c)-6(e)中的解密结果均未能恢复出原始图像，即只有当两个密钥全部正确时才能成功解密出原始图像。因此，通过矢量分解增加了系统密钥，拓展了系统密钥空间。

图5 加密及解密效果。(a)密文e(x,y);(b)解密图像

图6 密钥错误时的解密效果。(a)错误密钥k′(x1,y1);(b)错误密钥g2′(x,y);(c)使用k′(x1,y1)时的解密图像;(d)使用g2′(x,y)时的解密图像;(e)使用k′(x1,y1)和g2′(x,y)时的解密图像

3.2 抗攻击能力分析

首先对加密系统的抗噪声攻击能力进行分析。对图5(a)中的密文e(x,y)叠加不同强度的随机噪声，并对密文进行解密。所叠加的噪声是分布于[-0.5,0.5]区间的均值为0的均匀随机噪声，并用均方根差(root mean squared error)RMSE来描述所叠加的均匀随机噪声的强度，表示为

(9)

密文被叠加不同强度的噪声时的解密效果如图7所示，其中横轴为噪声的RMSE，纵轴为解密图像与原始图像之间的相关系数CC。可以看出，系统具有较好的解密效果，即使RMSE达到0.45时，解密图像仍然具有较高的CC值(0.815)。因此，加密系统具有较强的抗噪声攻击能力。

图7 解密图像CC与噪声RMSE关系曲线

对加密系统的抗剪切攻击能力进行分析。如图8所示对图5(a)中的密文e(x,y)进行剪切，并对密文进行解密。当密文被剪切为不同面积时的解密效果如图9所示，其中横轴为密文被剪切的面积百分比，纵轴为解密图像与原始图像之间的相关系数CC。可以看出，密文被剪切部分达到25%时，仍然能够较好地从密文中恢复出原始图像，具有较好的解密效果，因此，加密系统具有较强的抗剪切攻击能力。

图8 密文剪切示意图

图9 解密图像CC与密文剪切面积关系曲线

对加密系统的抗穷举攻击能力进行分析。图4(c)和图4(d)中的密钥相位模板g2(x,y)与k(x1,y1)的尺寸均为400×400像素，且密钥相位模板的位深为8位，即每个像素均有28=256阶相位值。密钥相位模板g2(x,y)与k(x1,y1)完全独立，因此，加密系统具有256400×400×2=256320000种密钥组合，即加密系统具有极大的密钥空间，因而对加密系统进行穷举攻击是不现实的，即加密系统具有抗穷举攻击能力。

对于唯密文攻击[27, 28]，其利用相位恢复算法恢复出原始图像。在本文加密系统中，原始图像本身并不直接参与加密，而是被分解为两个相位模板。即使通过相位恢复算法恢复出相位模板g1(x,y)，但由于无法得到密钥模板g2(x,y)，仍然无法恢复出原始图像。

对于已知明文攻击[29]和选择明文攻击[30,31]，其目的是通过已知或特定的明文-密文对恢复出密钥，并用于其它密文的解密。而由于密钥模板g2(x,y)并不参与图像的加密过程，即使通过攻击恢复出密钥模板k(x1,y1)，但由于攻击者无法得知密钥模板g2(x,y)，因此也无法从密文中解密出原始图像。