规则变型推理对远迁移问题解决的促进*

张 奇 张庆翔 张笑笑 高 超

规则变型推理对远迁移问题解决的促进*

张 奇1张庆翔1张笑笑2高 超3

(1辽宁师范大学心理学院, 大连 116029) (2深圳大学心理学院, 深圳 518060) (3江汉大学教育学院, 武汉 430056)

为了避免多重变异样例学习和采用题海战术, 并能促进规则样例学习的远迁移问题解决, 开创出原样例学习后对原型规则做出变型推理的学习方法, 以算术应用题的解题样例为原样例学习材料进行了4项实验研究。结果显示：四年级小学生运用该方法可有效促进远迁移问题的解决; 其变型推理能力存在数学成绩等级差异; 提供问题情境和推理提示能提高部分学生规则变型推理成绩和远迁移测验成绩。实验结果证明, 规则变型推理是促进远迁移问题解决的有效方法之一。

规则样例学习, 变型问题, 规则变型推理, 变型规则, 远迁移问题

1 引言

为了提高学生的问题解决能力, 尤其是为了提高新手或初学者的问题解决能力, 20世纪80年代兴起了样例学习研究(诸如：Sweller & Cooper, 1985; Lewis & Anderson, 1985; Lieberman, 1986; Cooper & Sweller, 1987; Zhu & Simon, 1987; Chi et al., 1989等)。在实验研究中, Sweller (1988, 1989, 2010)和Sweller等(1998)建立了认知负荷理论, 开发出多种样例设计方法, 将研究获得的许多新发现解释为“认知负荷效应” (Sweller, 2010; Sweller et al., 2019), 并将其转化为样例教学设计原则(Sweller, 2010; Renkl, 2011; 张奇等, 2018; Sentz et al. 2019; Rodiawati & Retnowati, 2019), 为学生问题解决能力的培养和教学设计做出了重要贡献。

张奇等(2012)发现, 在样例学习研究中隐含着两种性质不同的样例学习研究：一种是被试在学习或掌握了一般解题原理或解题规则前提条件下的样例学习研究; 另一种是被试在未学习或不了解一般解题原理或解题规则前提下的样例学习研究。他将前一种研究中的样例学习定义为“问题解决的样例学习”, 将后一种研究中的样例学习定义为“规则样例学习”。在此基础上, 他们开展了定义明确的规则样例学习研究, 并取得了丰硕成果。

大量实验研究结果表明, 不论是哪种样例学习, 被试在学习了一个解题样例之后都只能促进与样例问题结构特征相同的近迁移问题的解决, 但不能明显促进与样例问题结构特征不同的远迁移问题的解决。按照Sweller (2010)的观点, 要想促进远迁移问题的解决, 需要学习一系列结构特征变异问题的解题样例。但在实际教学中, 给学生设计并提供一系列结构特征变异的解题样例是不现实的。学生们的实际做法往往是在学习了一个解题样例之后, 寻找并尝试解决各种类型的变型问题。因此, 学生陷入“题海”并耗费大量的时间和精力。Renkl (2017)认为, 要想解决远迁移问题必须做深思熟虑的推理。但是, 他既没有指出具体的推理方法也没有指出研究途径。所以, 在既不提供一系列结构特征变异的解题样例又避免采用“题海战术”的情况下, 探索出有效促进规则样例学习远迁移问题解决的实际可行方法就成为样例学习研究中亟待解决的一个科学问题和教学实际问题。

为了探索促进规则样例学习远迁移问题解决的有效方法, 有人做了多重变异样例学习迁移效果的实验研究, 结果表明规则样例学习可以有效促进近迁移问题的解决, 但不能促进远迁移问题的解决。要想促进远迁移问题的解决需要学习二重变异和多重变异的解题样例(张奇, 赵弘, 2008)。还有人开展了小组合作规则样例学习迁移效果的实验研究, 结果表明, 小组合作的规则样例学习也只能促进近迁移问题的解决, 但对远迁移问题解决的促进作用并不明显(董成文, 张奇, 2018)。

我们在研究中发现：一个解题原理有几个变量就可以写出几个解题规则, 例如速度、时间和路程三者的关系原理有三个变量, 该原理就可以写出“速度 = 路程÷时间”、“路程 = 速度×时间”和“时间 = 路程÷速度”三个解题规则。如果学生学习该解题原理时最初习得的解题规则是“速度 = 路程÷时间”, 就可以将其称为“原型规则”, 而将另两个解题规则称为“变型规则”。解题规则的类型与问题类型或问题结构特征的类型是一一对应的, 诸如“已知物体运动的速度和时间、求路程的问题”只能用“路程 = 速度×时间”的解题规则来解决; “已知物体位移的距离和时间、求物体运动速度的问题”只能用“速度 = 路程÷时间”的解题规则来解决等。因此, 可以将原型规则解决的问题称为“原型问题”, 而将变型规则解决的问题称为“变型问题”。原型规则与变型规则可以相互转换, 即原型规则的解题公式可以通过等式变换得出变型规则的解题公式。当学生学习了一个原型规则之后遇到变型问题时, 如果他能够根据变型问题的结构特征将原型规则的解题公式转变为变型问题的解题公式, 就可称其对原型规则做出了“变型推理”或“规则变型推理”。如此说来, 如果学生能够进行规则变型推理, 就可以在原型规则的解题样例学习之后, 避开一系列结构特征变异问题的解题样例学习和通常所采用的题海战术, 通过规则变型推理解决变型问题, 产生远迁移效果。

根据上述设想, 我们定义了如下概念：(1)原型规则是指被试通过规则样例学习习得解题原理的首个解题规则。(2)“原样例”是用于习得原型规则的应用题解题样例。(3)原型问题就是原样例问题。(4)变型规则是原型规则的各种等式变换形式。(5)变型问题是用变型规则解决的问题。(6)规则变型推理或变型推理是根据变型问题的结构特征和等式变换原理, 将原型规则的解题公式转变为变型规则解题公式的推理过程。(7)“原样例学习”是被试对原型问题解题样例的学习。(8)“多重变异样例学习”是指被试在原样例学习之后, 再学习一系列结构特征变异的解题样例。(9)“近迁移问题”是原型问题的同构问题。(10)“远迁移问题”是原型问题的各种变型问题。

根据上述定义, 我们以“相向而行”和“同向而行”算术应用题解题样例做为两个原样例学习材料, 以没有学习过且不能解决这两种应用题的四年级小学生为被试, 进行了如下4项实验研究：实验1的三组被试在原样例学习后, 分别进行多重变异样例学习、规则变型推理和同构问题的解题练习, 然后通过迁移测验考察三种学习方法的迁移效果。实验目的是考察规则变型推理是否能够促进远迁移问题的解决。实验假设是三种学习方法的近迁移成绩无显著差异, 但远迁移成绩存在显著差异, 即多重变异样例学习对远迁移问题解决的促进作用最大; 规则变型推理的促进作用居其次; 同构问题解题练习的作用最小。实验2的目的是考察高、中、低三种数学考试成绩等级被试的规则变型推理成绩和远迁移测验成绩是否存在显著差异。实验假设是数学成绩高等级被试的规则变型推理成绩和远迁移测验成绩分别显著优于中等级和低等级被试; 中等级被试的两种成绩分别显著优于低等级被试。实验3在原样例学习之后, 给中、低数学成绩等级的被试设置三种问题情境(被试自编变型问题、主试给被试提供变型问题、主试给被试提供变型问题并要求被试对变型问题的类型做出划分), 使他们在三种不同问题情境下分别进行规则变型推理。实验目的是考察三种问题情境对规则变型推理成绩和远迁移测验成绩是否存在显著影响。实验假设中等级被试在三种问题情境下的规则变行推理成绩和远迁移测验成绩存在显著差异; 低等级被试在三种问题情境下的规则变行推理成绩和远迁移测验成绩均无显著差异。实验4在原样例学习之后, 给数学成绩低等级的被试提供8个变型问题并要求他们对其做出4种问题类型的划分。然后考察他们在有、无不完整解题规则提示条件下的规则变型推理成绩和远迁移测验成绩是否存在显著差异。实验目的是考察呈现不完整解题规则提示是否能够促进低等级被试的规则变型推理, 从而提高他们的规则变型推理成绩和远迁移测验成绩。实验假设是有提示组的规则变型推理成绩和远迁移测验成绩显著优于无提示组。

2 实验1：原样例学习后三种学习方法迁移成绩的比较

2.1 方法

2.1.1 被试

用G-Power软件计算出计划样本量为159人(Effect size= 0.25; α = 0.05, 1 − β = 0.80)。为使各组男女被试数量相等, 通过“前测”选取某城市普通小学四年级男、女生各81人(共162人)。分别对选出的男、女被试按照实验组别的数量进行1、2、3序号的重复编码。最后, 分别将序号相同的男、女被试分到多重变异样例学习组(简称“多重组”)、规则变型推理组(简称“推理组”)和同构问题解题练习组(简称“练习组”), 每组54人。男女各半。

2.1.2 实验材料

由前测材料、3种学习材料和迁移测验材料组成。

(1)前测材料：共5道测题, 前三道测题是被试已经学习过的单一交通工具行驶速度、时间和路程三者之间关系的算术应用题; 后两道测题是被试没有学习过的两个交通工具的“相向行驶”和“同向行驶”的算术应用题。

(2)学习材料：分为多重组、推理组和练习组三种学习材料。三种学习材料中均有相同的两个原样例, 分别是相向行驶问题和同向行驶问题的解题样例。多重组学习材料是在两个原样例学习之后给他们呈现的4道变型问题(相向行驶和同向行驶的变型问题各两道)的解题样例和指导语。推理组学习材料是在两个原样例学习之后, 鼓励他们对两个原型规则分别做出各种变型推理的指导语。练习组学习材料是在两个原样例学习之后给他们呈现的4道原型问题的同构问题(相向行驶和同向行驶的同构问题各两道)和指导语。

(3)迁移测验材料：共6道算术应用题, 其中2道近迁移测题和4道远迁移测题。2道近迁移测题分别是两个原样例问题的各一个同构算术应用题。4道远迁移测题分别是两个原样例问题的各两道变型算术应用题。

2.1.3 实验设计

为单因素被试间随机分组设计, 自变量是学习方法(多重变异样例学习、规则变型推理和解题练习), 因变量是近、远迁移测验成绩。

2.1.4 实验程序

分为前测阶段、学习阶段和迁移测验阶段。

(1)前测阶段：先于后两个阶段提前进行前测。首先给被试发放纸质前测材料。指导语要求备选学生在5分钟之内解答5道前测题。5分钟后主试收回答卷并评定成绩。选择能够正确解答前三道测题, 但不能正确解答后两道测题的学生作为实验的被试, 并按照其编码将其分配到多重组、推理组和练习组。各组被试人选确定后, 进入下面的实验程序。

(2)学习阶段：三组被试在不同的教室里同时进行学习阶段和迁移测验阶段的实验程序。学习阶段的前10分钟三组被试都学习相同的两个原样例。10分钟之后, 主试回收样例学习材料, 进入下一步：多重组被试接着学习4个变型问题的解题样例; 推理组被试对原型规则做出各种变型推理, 分别写出变型规则的解题公式; 练习组解答4道同构问题。时间均为10分钟。

(3)迁移测验阶段：学习阶段结束后, 全体被试接着在指导语的要求下同时进行20分钟的迁移测验。

2.1.5 计分标准

学习阶段的计分标准为推理组被试正确写出一个变型规则的计算公式计1分, 错误计0分, 满分为4分。练习组的被试正确解答出一个练习题计1分, 答错或没答计0分, 满分为4分。迁移测验的计分标准为被试每答对1题计1分, 答错或没答的计0分。近迁移测验满分为2分, 远迁移测验满分为4分。

2.2 结果与分析

三个组被试的近、远迁移测验成绩的描述统计和方差分析结果见图1。

单因素方差分析结果显示：三种学习方法的近迁移测验成绩差异不显著,(2, 159) = 1.71,> 0.05; 远迁移测验成绩差异显著,(2, 159) = 74.35,< 0.001, η2= 0.48, 事后分析(Thamhane)结果显示, 多重组显著高于推理组,< 0.001, 95% CI = [0.57, 1.76]和练习组,< 0.001, 95% CI = [2.20, 3.09]; 推理组显著高于练习组,< 0.001, 95% CI = [0.95, 2.02]。

2.3 讨论

实验1结果表明, 在原样例学习之后, 多重变异样例学习的远迁移效果最好, 规则变型推理的远迁移效果居中, 同构问题解题练习的远迁移效果最差。

上世纪的样例学习实验研究就证明, 学习问题结构特征变异的解题样例能促进远迁移问题的解决(Cormier & Hagman, 1987; Jelsma & van Merrienboer, 1990; Singley & Anderson, 1989; Paas & van Merriënboer, 1994)。后来的实验结果也表明, 问题结构特征变异的样例学习能够促进远迁移问题的解决(张奇, 赵弘, 2008; Sweller et al., 2019)。Sweller (2010)将其称为“变异性效应”(variability effect), 并用认知负荷理论解释了该效应。

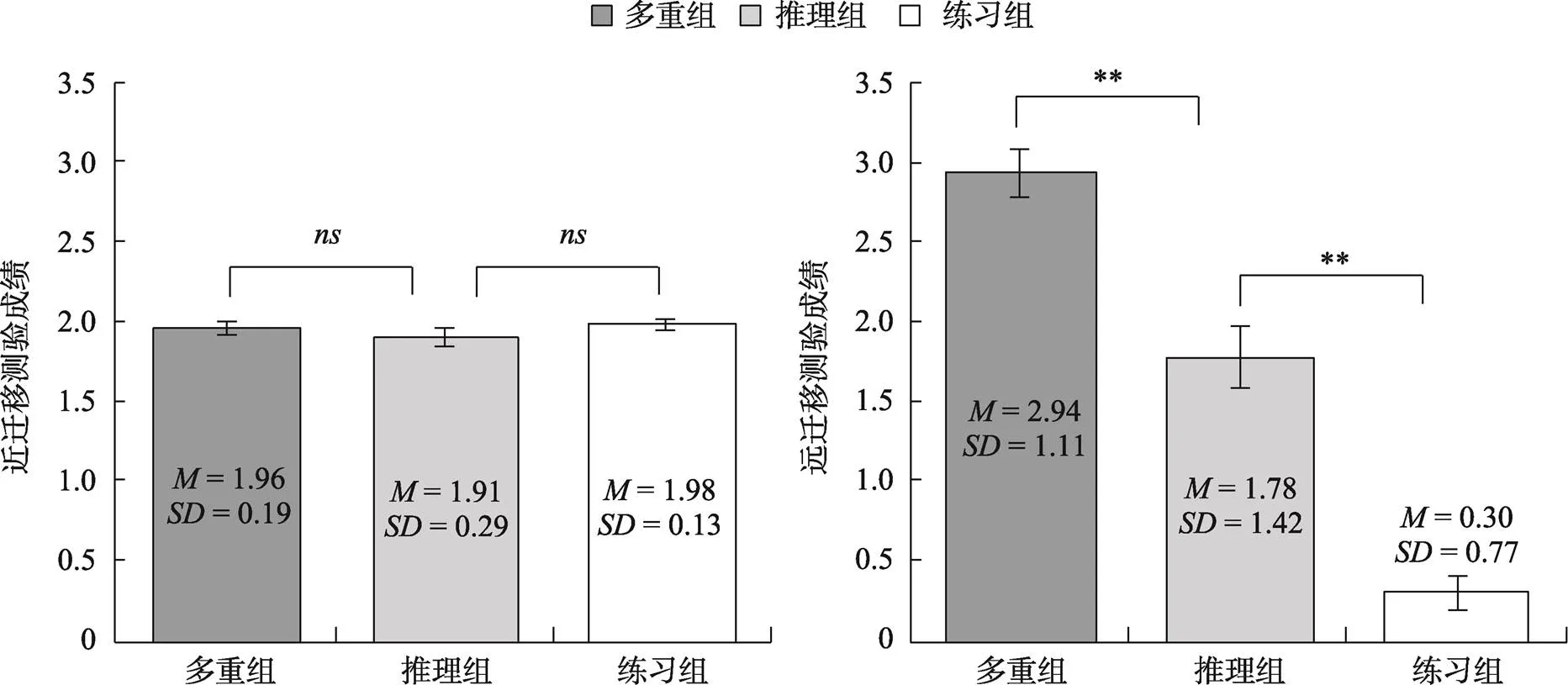
图1 三组被试近、远迁移测验成绩的均值、标准差及方差分析结果

注：为> 0.05;**为< 0.01; 误差线为标准误。

多重组被试学习了原样例之后, 又学习了4个变型问题的解题样例, 使他们既学习了变型问题的结构特征又学习了与之对应的解题规则, 促进了较多被试的规则变型推理。所以, 该组被试的远迁移测验成绩最好。

推理组的被试在原样例学习之后, 在既无变型问题也无解题规则参照的条件下尝试对原型规则进行各种变型推理, 这比多重组被试从变异样例中学习规则变型推理的难度大很多。因此, 与多重组相比, 该组有较多的被试不能完成规则变型推理也不能正确解决远迁移问题。所以, 该组的远迁移测验成绩明显不如多重组好。

练习组被试在原样例学习之后专注于同构问题的解题练习, 既没有思考如何做出规则变型推理, 也没有思考如何解决变型问题, 所以, 他们的远迁移测验成绩最差。

推理组的远迁移成绩虽然不如多重组好, 但这并不意味着规则变型推理这种学习方法的远迁移效果比多重组差。而是因为在既无变型问题也无解题规则参照的条件下尝试对原型规则进行各种变型推理的难度很大。如果寻找到培养和提高学生规则变型推理能力的有效方法就能够提高他们的规则变型推理成绩和远迁移测验成绩。考虑到有研究表明, 学生的推理能力与学业成绩之间存在显著的正相关(张军翎, 2008; 王光明等, 2016)。由此可推论得出, 被试间规则变型推理的能力差异也可能表现为他们在数学考试成绩等级之间的差异。因此, 实验2考察规则变型推理成绩在被试数学考试成绩等级之间的差异, 以及规则变型推理成绩与远迁移测验成绩之间的关系。

3 实验2：变型推理成绩和远迁移成绩在数学成绩等级之间的差异

3.1 方法

3.1.1 被试

用G-Power软件计算出的计划样本量是159人(Effect size= 0.25; α = 0.05, 1 − β = 0.80)。按前两次数学考试成绩的平均分将城市普通小学四年级学生分为高(90分以上)、中(75至85分)、低(60至70分)三个数学成绩等级。为使各组男女被试数量相等, 通过前测分别从高、中、低三个数学成绩等级的学生中各选取54名被试(男女各27人), 分为高分组、中分组和低分组。

3.1.2 实验材料

与实验1中推理组的实验材料相同。

3.1.3 实验设计

为单因素被试间分组实验设计, 自变量为数学成绩等级(高分组、中分组和低分组), 因变量是近、远迁移测验成绩。

3.1.4 实验程序

与实验1推理组的实验程序相同。

3.1.5 计分标准

与实验1推理组的计分标准相同。

3.2 结果与分析

(1)规则变型推理成绩的差异分析

三组被试的规则变型推理成绩的描述统计及方差分析结果见图2。

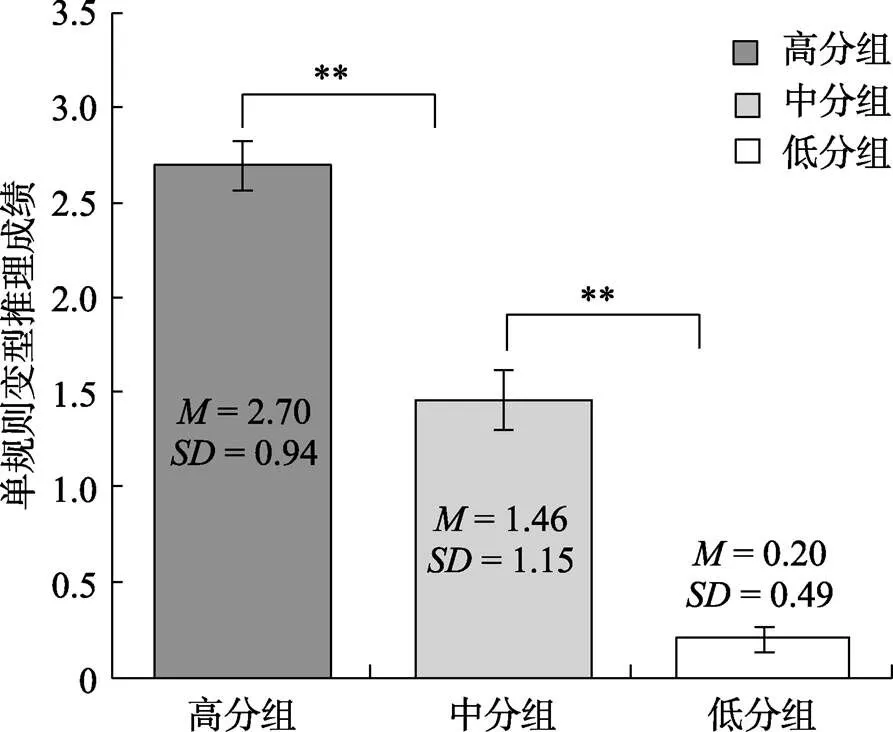
图2 三组被试规则变型推理成绩的均值、标准差及方差分析结果

注：**为< 0.01; 误差线为标准误。

单因素方差分析结果显示, 三组被试的变型推理成绩差异显著,(2, 161) = 103.64,< 0.001, η2= 0.56, 事后分析(Thamhane)结果显示, 高分组的推理成绩显著高于中分组,= < 0.001, 95% CI = [0.75, 1.73]和低分组,< 0.001, 95% CI = [2.15, 2.85]; 中分组的推理成绩显著高于低分组,< 0.001, 95% CI = [0.84, 1.67]。

(2)近、远迁移测验成绩的差异分析

三组被试近、远迁移测验成绩的描述统计及方差分析结果见图3。

单因素方差分析结果显示：三组被试的近迁移测验成绩差异显著,(2, 161) = 12.23,< 0.001, η2= 0.13, 事后分析(Thamhane)结果显示, 高分组的近迁移成绩显著高于低分组,< 0.01, 95% CI = [0.12, 0.58]; 中分组的近迁移成绩也显著高于低分组,< 0.01, 95% CI = [0.08, 0.55]; 高分组与中分组之间的近迁移成绩差异不显著,> 0.05。

三组被试的远迁移测验成绩差异显著,(2, 161) = 149.74,< 0.001, η2= 0.65, 事后分析(Thamhane)结果显示, 高分组的远迁移成绩显著高于中分组,< 0.001, 95% CI = [1.06, 1.90]和低分组,< 0.001, 95% CI = [2.36, 2.93]; 中分组的远迁移成绩显著高于低分组,< 0.001, 95% CI = [0.76, 1.57]。

(3)变型推理成绩与远迁移测验成绩之间的回归分析

回归分析结果显示, 全体被试的变型推理成绩与其远迁移测验成绩的回归方程和解释率为：0.39 + 0.86,20.756, 其中分别代表各组的远迁移测验成绩,代表其变型推理成绩。

3.3 讨论

实验2结果表明, 高分组的变型推理成绩和远迁移测验成绩均分别显著优于中分组和低分组; 中分组的两个成绩均显著优于低分组。回归分析结果表明, 被试的规则变型推理成绩与远迁移测验成绩存在显著的线性因果关系。被试的规则变型推理成绩可以预测其远迁移测验成绩, 即规则变型推理成绩是因, 远迁移测验成绩是果的因果关系。由此可以推论得出规则变型推理能力与数学考试成绩等级之间的因果关系。数学试题不论其题型和内容如何, 均可视为由远、近迁移试题构成。解决近迁移试题需要同构类比的推理能力。已往的实验研究结果(张奇, 赵弘, 2008; 董成文, 张奇, 2018)以及实验1和实验2的结果均表明, 小学生具有同构类比的推理能力, 一般可以解决近迁移试题。只是数学考试成绩低等级被试的同构类比的推理能力较低, 所以, 近迁移成绩较差(详见实验2的结果分析)。假如考生在数学考试中的近迁移测验成绩无显著差异的话, 那么, 数学考试成绩的显著差异主要就是由远迁移测验成绩决定的。由于远迁移试题的解决需要规则变型推理, 所以, 数学成绩的高低就主要是由考生规则变型推理能力的高低决定的。由此看来, 考生同构类比的推理能力(即近迁移试题的解决能力)和规则变型推理能力(即远迁移试题的解决能力)的高低就是其数学考试成绩高低的决定因素, 而不是数学考试成绩等级的高低决定考生规则变型推理能力的高低。所以, 培养和提高学生的规则变型推理能力就成为提高其远迁移问题解决能力和数学考试成绩的主要途径之一。

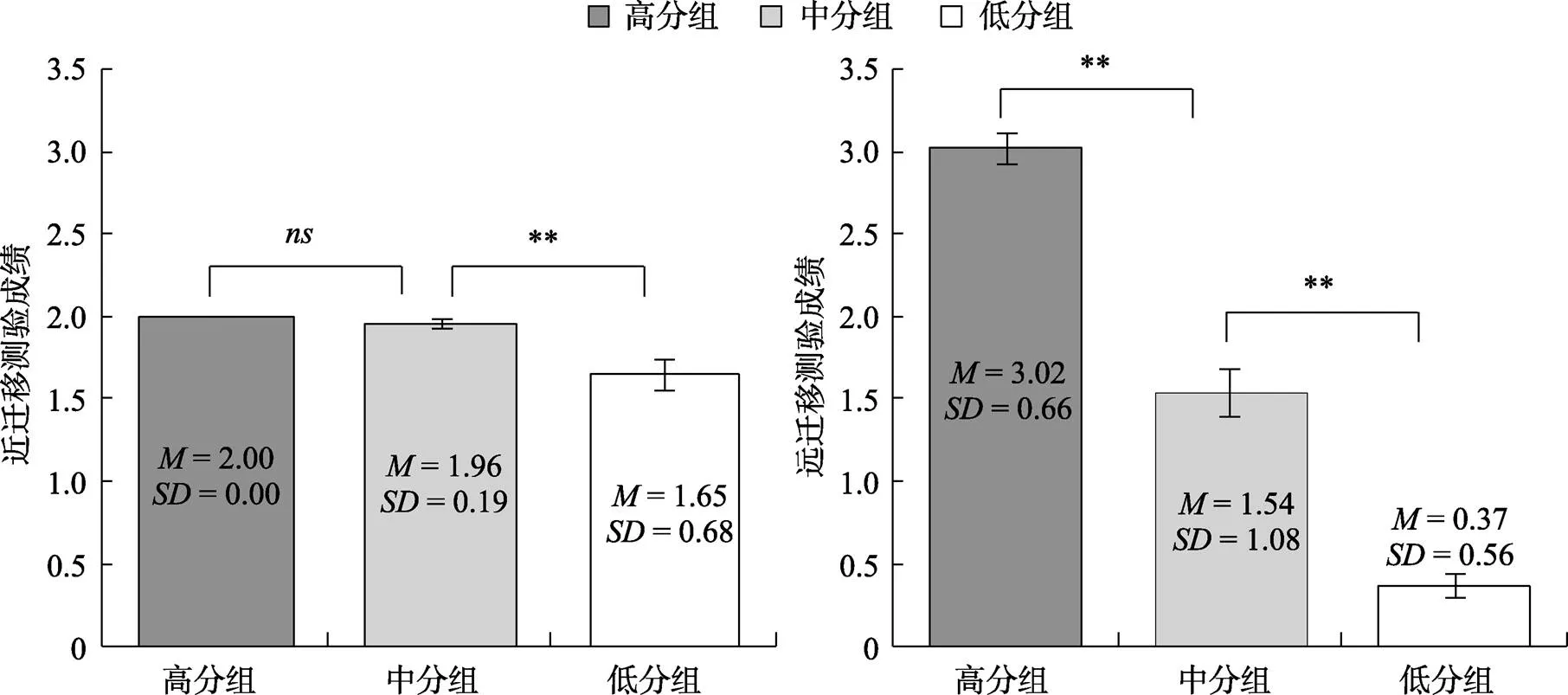
图3 三组被试近、远迁移成绩的均值、标准差及方差分析结果

注：为> 0.05;**为< 0.01; 误差线为标准误。

实验2的结果表明, 高分组的规则变型推理成绩显著优于中分组和低分组。因此, 有必要培养和提高中分组和低分组被试的规则变型推理能力并提高其变型推理成绩, 进而促进远迁移问题的解决并提高远迁移测验成绩。所以, 实验3将给中、低分组被试提供三种问题情境, 考察哪种问题情境能够更有效地促进他们的规则变型推理, 从而提高其变型推理成绩和远迁移测验成绩。

4 实验3：三种问题情境下规则变型推理对远迁移问题解决的促进

4.1 方法

4.1.1 被试

按实验2的方法选取中、低分组被试, 再将中、低分组被试分别随机分到“自编变型问题组”、“呈现变型问题组”和“变型问题分类组”, 实验共6组被试。用G-Power计算出的计划样本量为158人(Effect size= 0.25; α = 0.05, 1 − β = 0.80)。为使各组男女被试人数相等, 通过前测选取某城市普通小学四年级学生180人(男女各90人), 每组被试30人。

4.1.2 实验材料

包括前测材料、原样例学习材料、问题情境材料和迁移测验材料。

(1)前测材料和原样例学习材料均与实验1相同。

(2)问题情境材料分为三种：①自编变型问题组的被试在原样例学习之后, 要求他们根据原型问题自编出各种变型问题。因此, 该组的问题情境材料就是要求被试自编变型问题的指导语。②呈现变型问题组的问题情境材料是给被试呈现的4种类型的变型问题, 相向行驶和同向行驶的变型问题各两道及指导语。③变型问题分类组的问题情境材料是给被试呈现4种类型(相向行驶和同向行驶的变型问题各两种类型)、每种类型各2道的共8道变型问题及问题分类作业的指导语。每2道同类型问题的结构特征相同, 只是表面特征不同。8道变型问题分左、右两列呈现给被试, 每列各有4道不同类型的变型问题从上到下随机排列。指导语要求被试给左、右两列的同类型问题画线连接起来, 共需要画出4条连线。所以, 该组只比呈现变型问题组多做了问题类型划分的作业, 但变型推理的作业数量和类型都相同。

(3)迁移测验材料与实验1相同。

4.1.3 实验设计

为2×3两因素被试间分组设计, 自变量1为数学成绩等级, 分为中分组和低分组两个水平; 自变量2为问题情境类型, 分为自编应用题、呈现问题和呈现问题并分类三种情境; 因变量是近、远迁移测验成绩。

4.1.4 实验程序

分为前测阶段、原样例学习阶段、规则变型推理阶段和迁移测验阶段。

(1)前测、样例学习和迁移测验阶段均与实验2相同。

(2)规则变型推理阶段是被试在学习完原样例之后, 分别在三种不同的问题情境下进行规则变型推理。具体来说：①自编变型问题组的被试针对自己编出的变型问题进行规则变型推理; ②呈现问题组的被试针对呈现的变型问题进行规则变型推理; ③呈现变型问题并分类组的被试在原样例学习之后, 首先对呈现的8个变型问题做出4种类型的划分, 然后再针对4种变型问题进行规则变型推理。三组被试按照规定的时间, 结束规则变型推理作业后进入迁移测验。

4.1.5 计分标准

规则变型推理成绩和迁移测验成绩的计分标准均与实验2相同。

4.2 结果与分析

(1)规则变型推理成绩的差异检验

三种问题情境下中、低分组被试规则变型推理成绩的描述统计及方差分析结果见图4。

二因素方差分析结果显示：规则变型推理成绩在三种问题情境之间差异显著,(2, 179) = 7.87,< 0.01, ηp2= 0.083; 在数学成绩等级之间差异显著,(1, 179) = 127.67,0.001, ηp2= 0.423; 问题情境与数学成绩等级对规则变型推理成绩的交互作用显著,(2, 179) = 7.65,< 0.01, ηp2= 0.081。简单效应分析结果显示：中等级被试在对呈现的变型问题做出分类的条件下, 规则变型推理成绩显著优于仅呈现变型问题和自编变型问题的规则变型推理成绩,(2, 179) = 15.30,< 0.01, ηp2= 0.15; 低等级被试三种问题情境下的规则变型推理成绩差异不显著,(2, 179) = 0.22,> 0.05。

(2)近、远迁移测验成绩的描述统计及方差分析

三种问题情境下中分组被试和低分组被试的近迁移测验成绩和远迁移测验成绩的描述统计及方差分析的结果见图5和图6。

二因素方差分析结果显示：近迁移测验成绩在三种问题情境之间的差异不显著,(2, 179) = 0.606,> 0.05; 在数学成绩等级之间差异显著,(1, 179) = 16.39,< 0.001, ηp2= 0.086; 问题情境与数学成绩等级对近迁移测验成绩的交互作用不显著,(2, 179) = 0.89,> 0.05。

远迁移测验成绩在三种问题情境之间的差异显著,(2, 179) = 16.58,< 0.001, ηp2= 0.16; 在数学成绩等级之间差异显著,(1, 179) = 148.18,< 0.001, ηp2= 0.46; 问题情境与数学考试成绩等级对远迁移测验成绩的交互作用显著,(2, 170) = 8.86,< 0.001, ηp2= 0.092。简单效应分析结果显示：中等级被试在对呈现的变型问题做出分类的条件下, 远迁移测验成绩显著优于仅呈现变型问题和自编变型问题的远迁移测验成绩,(2, 179) = 24.16,< 0.001, ηp2= 0.22; 低等级被试三种问题情境下的远迁移测验成绩差异不显著(2, 179) = 1.28,> 0.05。

4.3 讨论

实验3结果表明, 中分−变型问题分类组被试的规则变型推理成绩和远迁移测验成绩显著高于另两组; 中分−呈现变型问题组被试的规则变型推理成绩和远迁移测验成绩显著高于中分−自编应用题组。这是因为四年级学生在原样例学习之后, 自编变型应用题还比较困难或者用时较多。因此, 在有限的时间内, 这种方法不利于培养和提高他们的规则变型推理能力。只呈现变型问题而不做问题类型划分也不利于被试针对变型问题的类型做出规则变型推理。因此, 对于中分组被试来说, 给他们呈现具体变型问题并要求他们对其做出类型划分, 然后分别针对不同类型的变型问题做出规则变型推理是培养和提高他们规则变型推理能力的一种有效方法。

图4 三种问题情境下规则变型推理成绩的均值、标准差及方差分析结果

注:**为< 0.01;为> 0.05; 误差线为标准误。

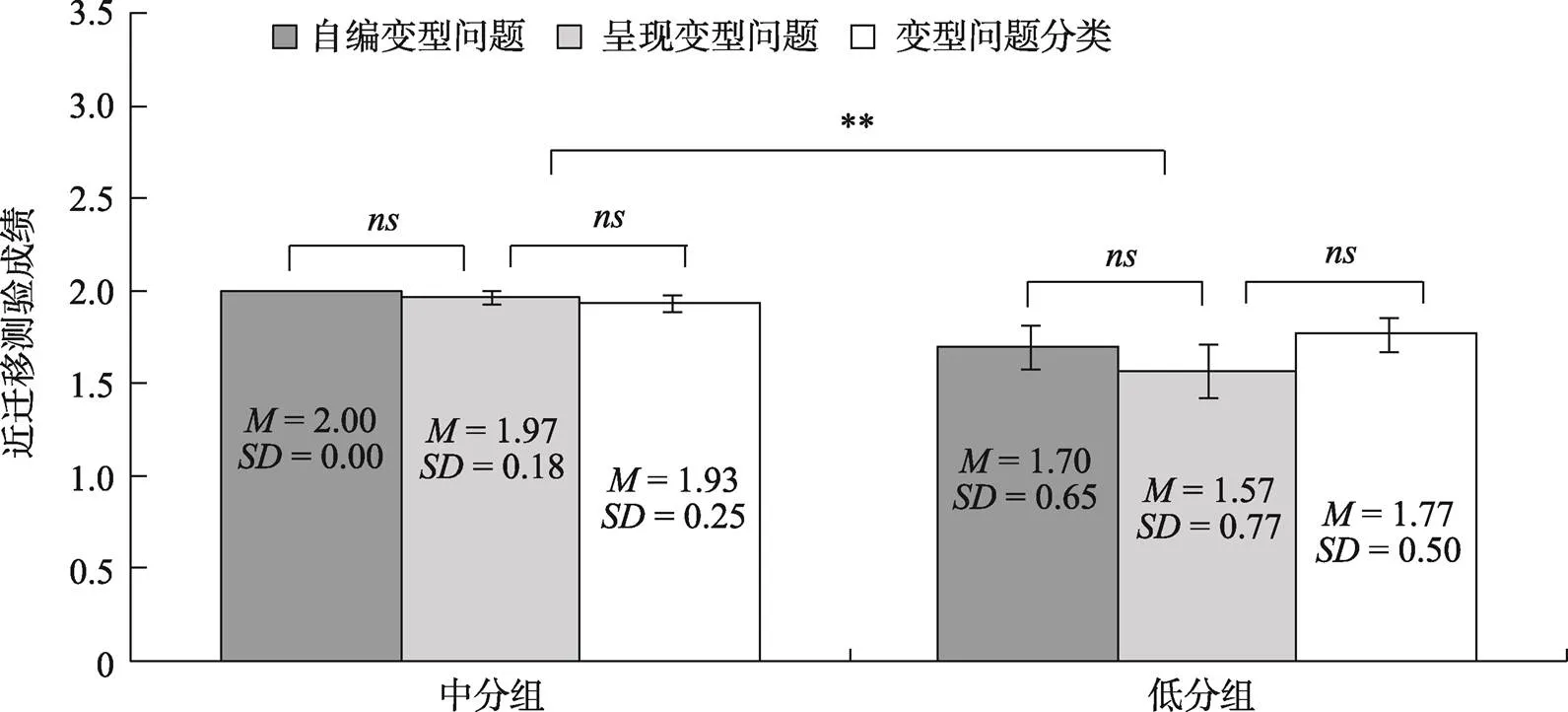
图5 三种问题情境下近迁移测验成绩的均值、标准差及方差分析结果

注:为> 0.05;**为< 0.01; 误差线为标准误。

图6 三种问题情境下远迁移测验成绩的均值、标准差及方差分析结果

注:**为< 0.01;为> 0.05; 误差线为标准误。

实验3结果还表明, 不论哪种问题情境, 中分组被试的规则变型推理成绩和迁移测验成绩均显著高于低分组被试。此结果再次证明, 学生的数学成绩等级是由其规则变型推理能力的高低决定的。而且, 低分组被试的规则变型推理成绩和迁移测验成绩在三种不同问题情境之间均无显著差异。这说明只提供问题情境不足以培养和提高数学成绩低等级学生的规则变型推理能力。在教学实践中, 培养数学成绩低等级学生的规则变型推理能力可以采用教师指导、同伴辅导和推理提示等方法。由于实验中的规则变型推理有时间限制并需要被试独立完成推理作业, 所以, 采用了后一种方法, 即给他们提供促进其规则变型推理的提示条件。为此, 实验4以低分组学生为被试, 在原样例学习后, 给他们呈现变型问题并要求他们划分问题类型; 然后, 针对各种变型问题给他们提供不完整的解题规则, 使他们在不完整解题规则的提示下做出规则变型推理, 以此促进他们对远迁移问题的解决。所以, 实验4的目的就是考察不完整解题规则的提示能否促进低分组被试的规则变型推理, 进而提高远迁移测验成绩。

5 实验4：问题情境下有提示的规则变型推理对变型问题解决的促进

5.1 方法

5.1.1 被试

按实验2的方法选取数学考试成绩低等级的被试, 再将其随机分为“问题分类组”和“提示推理组”, 实验共2组被试。用G-Power计算出计划样本量为78人(Effect size= 0.65; α = 0.05, 1 − β = 0.80)。为使各组男女被试数量相等, 通过“前测”选取某城市普通小学四年级学生80人(男女各40人); 每组被试40人。

5.1.2 实验材料

分为前测材料、原样例材料、问题情境材料、推理提示材料和迁移测验材料。

(1)前测材料、原样例学习材料、问题情境材料和迁移测验材料均与实验3的变型问题分类组的材料相同。

(2)两组被试在变型推理阶段的材料不同：①问题分类组(即“无提示推理组”)在完成问题类型划分之后即可对4种变型问题做出规则变型推理。②提示推理组在完成问题类型划分后, 主试给每种变型问题提供一个不完整的解题规则, 要求被试参照不完整解题规则做出规则变型推理, 即将不完整的解题规则补充完整。

5.1.3 实验设计

为单因素被试间随机分组设计, 自变量是学习方法(问题分类和提示推理), 因变量是近迁移测验成绩和远迁移测验成绩。

5.1.4 实验程序

分为前测阶段、学习阶段和迁移测验阶段。

(1)前测阶段和迁移测验阶段均与实验1相同。

(2)学习阶段, 将两组被试安排在不同的教室里同时学习。前10分钟两组被试都学习相同的原型问题解题样例。10分钟之后, 主试回收样例学习材料, 进行下一步学习：给两组被试呈现8道变型问题, 并要求被试对这8道题做出4种类型的划分。分类作业完成后, 问题分类组被试做4种变型问题的规则变型推理; 主试给提示推理组的被试提供4种变型问题的不完整解题规则, 并要求被试在不完整解题规则的提示下做4种规则变型推理。两组被试学习阶段的时间均为25分钟。

5.1.5 计分标准

问题分类成绩的计分标准为, 被试每正确完成一种问题的分类计1分, 分类错误或没有分类计0分。问题分类作业成绩满分为4分。推理成绩的计分标准为被试每正确推理得出(或补全)一个变型规则的计算公式计1分, 推理错误(或没有补全)计0分, 推理成绩满分为4分。迁移测验成绩的计分标准与实验3相同。

5.2 结果与分析

(1)两组被试问题分类作业成绩见图7。

单因素方差分析结果显示, 提示推理组和问题分类组的问题分类成绩差异不显著,(1, 79) = 0.70,> 0.05。

(2)两组被试规则变型推理成绩见图8。

单因素方差分析结果显示, 提示推理组的规则变型推理成绩显著优于问题分类组,(1, 79) =151.95,< 0.001, η2= 0.66。

(3)两组被试近、远迁移测验成绩见图9。

图7 两组被试的问题分类作业成绩的均值、标准差及方差分析结果

注:为> 0.05; 误差线为标准误。

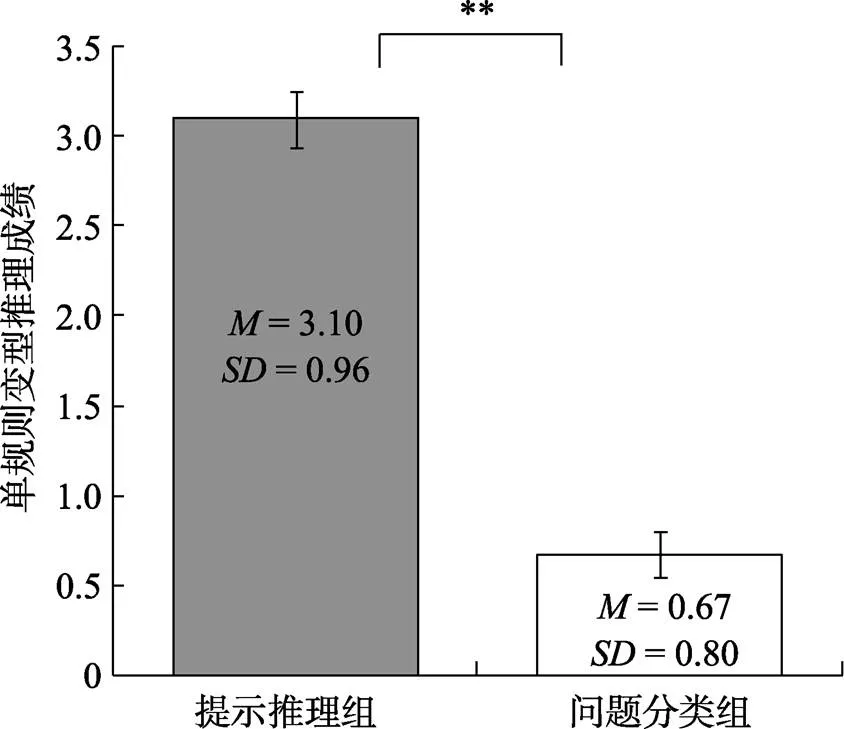
图8 两组被试规则变型推理成绩的均值、标准差及方差分析结果

注:**为< 0.01; 误差线为标准误。

图9 两组被试近、远迁移测验成绩的均值、标准差及方差分析结果

注:为> 0.05;**为< 0.01; 误差线为标准误。

单因素方差分析结果显示, 两组的近迁移测验成绩差异不显著,(1, 79) = 0.06,> 0.05; 两组的远迁移测验成绩差异显著,(1, 79) = 180.78,< 0.001, ηp2= 0.70, 提示推理组的远迁移成绩显著优于问题分类组。

5.3 讨论

实验4结果表明, 与没有推理提示的问题分类组相比, 推理提示组的规则变型推理成绩和远迁移测验成绩都有了显著提高。这说明“推理提示法”有效地培养和提高了低分组被试的规则变型推理能力, 从而提高了其远迁移问题的解决能力。因为, “推理提示”给他们呈现了解决变型问题的不完整解题规则。不完整的解题规则能够提示和辅助他们做出规则变型推理, 从而提高了他们的远迁移测验成绩。

6 综合讨论

6.1 规则样例学习的近迁移效应

4项实验结果均表明, 四年级小学生学习一个原样例之后就能明显促进近迁移问题的解决, 使解题规则的样例学习产生近迁移效果。这是因为近迁移问题的结构特征与他们所学的原型问题的结构特征相同。问题的结构特征相同, 解题规则也相同。学生只要认识到这一点, 就可以用原样例中的原型规则解决近迁移问题。以往的规则样例学习研究也证明了这一点(张奇, 赵弘, 2008; 董成文, 张奇, 2018)。在上世纪的样例学习研究中就发现了“样例效应” (worked example effect)。该效应是指：当学习过一般解题原理或解题样例的学生最初运用原理解决具体问题时, 学习解题样例的学生比没有学习解题样例而直接解决问题学生的学习效果更好(Cooper & Sweller, 1987)。后来的样例学习研究均表明, 学习解题样例均能促进近迁移问题的解决、产生近迁移效果(Sweller, 2010)。为了有别于样例学习的样例效应, 可以把规则样例学习的近迁移效果称为“近迁移效应”。

6.2 规则变型推理对远迁移问题解决的促进作用

实验1结果表明, 在原型样例学习之后, 鼓励学生尽可能地对原型规则做出各种变型推理, 可以促进其变型问题的解决, 产生远迁移效果。实验2的结果表明, 数学成绩等级越高的学生其变型推理成绩越高, 远迁移测验成绩也越高。实验3的结果表明, 在原样例学习之后, 给数学成绩中等级的学生呈现各种变型问题并要求他们对变型问题做出类型划分, 可以有效提高它们的变型推理成绩和远迁移测验成绩。实验4的结果表明, 给数学成绩低等级的学生呈现各种变型问题并要求他们对这些问题进行类型划分。然后, 针对不同类型的变型问题给他们提供不完整的解题规则, 使他们在不完整解题规则的提示下做出规则变型推理。该方法也能明显促进他们的规则变型推理, 进而产生远迁移效果。4项实验结果均表明, 被试的规则变型推理成绩越高, 远迁移测验成绩就越高。实验3和实验4的结果进一步证明, 培养和提高学生的规则变型推理能力是提高其远迁移问题解决能力的有效途径之一。

6.3 实验研究的教学启示

在教学实践中, 给小学生编制和呈现一系列变型问题的解题样例, 供他们进行多重变异样例学习是不现实的。与之相比, 鼓励、辅助和提示学生对学习过的原型规则做出各种变型推理就是提高他们远迁移问题解决能力的一种实际可行的有效方法。其实, 不论是多重变异样例学习还是规则变型推理, 最后都是用变型规则解决变型问题。只是通过多重变异样例学习更容易使学生做出规则变型推理。但是, 这需要教师编制大量解题样例。所以, 这种方法既不现实也不利于学生变型推理能力的培养, 更不利于学生学习主观能动性的发挥。而鼓励、辅助和提示学生做出规则变型推理的教学方法既能发挥学生学习的主观能动性, 又有利于学生变型推理能力的培养和提高。因此, 教师们采用各种有效的方法(指导和辅助学生做出规则变型推理的方法很多, 有待教师们在实践中开发和利用), 鼓励、辅助和提示学生对原型规则做出各种变型推理就是提高其解决远迁移问题解决能力的一种实际可行的途径和有效方法。而多重变异样例学习可以作为帮助变型推理能力低下的学生学习规则变型推理的必要补充方法。

6.4 研究局限与展望

如果按照解题规则数量的多少划分问题的类型, 可将问题划分为“单规则”问题(即用一个规则解决的问题)和“组合规则”问题(即用两个或两个以上的规则组合起来解决的问题); 在组合规则问题中既有同一知识领域的规则组合问题, 也有不同知识领域的规则组合问题, 还有跨学科的规则组合问题等等。本研究只考察了单规则变型推理对单规则变型问题解决的促进作用。后续研究可以考察各种组合规则的变型推理对其变型组合问题解决的促进作用。本研究结果表明, 被试对原型规则做出变型推理可以有效促进变型单规则问题的解决, 使规则样例学习产生远迁移效果。如果后续研究得出各种组合规则的变型推理能有效促进其变型组合问题的解决并产生远迁移效果, 则可得出规则变型推理是促进其变型问题解决并产生远迁移效果的有效方法的一般性结论, 并用于培养和提高学生的问题解决能力的教学实践。此为该项研究的深远意义之所在。

7 结论

(1)四年级小学生在原样例学习之后, 针对各种变型问题做出原型规则的各种变型推理, 可以有效促进与之对应的远迁移问题的解决。

(2)四年级小学生的规则变型推理成绩和远迁移测验成绩存在显著的数学考试成绩等级差异。数学考试成绩等级越高的学生, 规则变型推理的成绩和远迁移测验成绩越高。

(3)对于数学考试成绩中等级的学生, 在原样例学习之后, 给他们呈现各种变型问题, 并要求他们划分问题类型, 可以有效地促进他们的规则变型推理, 并显著地提高远迁移测验成绩。

(4)对于数学考试成绩低等级的学生, 在原样例学习之后, 给他们呈现各种变型问题并要求他们划分问题类型, 再给他们提供不完整解题规则作为推理提示, 就可以有效地促进他们的规则变型推理, 并显著地提高远迁移测验成绩。

Chi, M. T., Bassok, M, Lewis, M. W., Reimann, P. & Glaser, R. (1989). Self-explanations: How students study and use examples in learning to solve problems.(2), 145−182.

Cooper, G., & Sweller, J. (1987). Effects of schema acquisition and rule automation on mathematical problem-solving transfer.(4), 347−362.

Cormier, S. M., & Hagman, J. D. (1987).San Diego: Academic Press.

Dong, C. W., & Zhang, Q. (2018). Transfer effect of rule worked example learning of individual and group cooperation.,(5), 53−64.

[董成文, 张奇. (2018). 个体与小组合作的规则样例学习的迁移效果.(5), 53−64.]

Jelsma, O., & van Merrienboer, J. J. (1990). The ADAPT design model: Towards instructional control of transfer.(2), 89−120.

Lewis, M. W., & Anderson, J. R. (1985). Discrimination of operator schemata in problem solving: Learning from examples.(1), 26−65.

Lieberman, H. (1986). An example based environment for beginning programmers.(3-4), 277−292.

Paas, F., & van Merriënboer, J. J. G. (1994). Variability of worked examples and transfer of geometrical problem- solving skills: A cognitive-load approach.,(1), 122−133.

Renkl, A. (2011). Instruction based on examples. In R. E. Mayer, & P. A. Alexander (Eds.),(pp.272−295). New York: Routledge.

Renkl, A. (2017). Learning from worked-examples in mathematics: Students relate procedures to principles., 571−584.

Rodiawati, A., & Retnowati, E. (2019). How to design worked examples for learning patterns in mathematics., 012045.

Sentz, J., Stefaniak, J., Baaki, J., & Eckhoff, A. (2019). How do instructional designers manage learners’ cognitive load? An examination of awareness and application of strategies.(1), 199−245.

Singley, M. K., & Anderson, J. R. (1989).(No. 9). New York: Harvard University Press.

Sweller, J. (1988). Cognitive load during problem solving: Effects on learning.,(2), 257−285.

Sweller, J. (1989). Cognitive technology: Some procedures for facilitating learning and problem solving in mathematics and science.,(4), 457−466.

Sweller, J. (2010). Element interactivity and intrinsic, extraneous, and germane cognitive load.,(2), 123−138.

Sweller, J. & Cooper, G. A. (1985). The use of worked examples as a substitute for problem solving in learning algebra.(1), 59−89.

Sweller, J., van Merrienboer, J., & Paas, F. (1998). Cognitive architecture and instructional design.,(3), 251−296.

Sweller, J., van Merrienboer, J., & Paas, F. (2019). Cognitive architecture and instructional design: 20 years later.(1), 261−292.

Wang, G. M., Zhang, X. M., & Wang, Z. Y. (2016). A study on the intelligence characteristics of high school students efficient mathematic learning.(3), 48−55.

[王光明, 张晓敏, 王兆云. (2016). 高中生高效率数学学习的智力特征研究.(3), 48−55.]

Zhang, J. L. (2008). The comparison of primary and middle school student’s logical reasoning ability, metacognition and attention level with their academic performance.,(3), 707−710.

[张军翎. (2008). 中小学生的逻辑推理能力、元认知及注意力水平与学业成绩的比较.(3), 707−710.]

Zhang, Q., Dong, C. W., & Zhang, Q. X., (2018). The effect of worked example learning and principles of instructional design.(1)32−46.

[张奇, 董成文, 张庆翔. (2018). 样例学习效应与教学设计原则.(1), 32−46.]

Zhang, Q., Wan, Y., Lin, H. X., & Qu, K. J. (2012). The worked-example learning theoretical research on the mathematical operation rules.,(1), 47−53.

[张奇, 万莹, 林洪新, 曲可佳. (2012). 数学运算规则样例学习的理论探索.,(1), 47−53.]

Zhang, Q., & Zhao, H. (2008). Transfer effect of double variant worked example learning for arithmetic word problems.(4), 409−417.

[张奇, 赵弘. (2008). 算术应用题二重变异样例学习的迁移效果.(4), 409−417.]

Zhu, X., & Simon, H. A. (1987). Learning mathematics from examples and by doing.(3), 137−166.

Effects of rule variant reasoning in far transfer problem solving

ZHANG Qi1, ZHANG Qingxiang1, ZHANG Xiaoxiao2, GAO Chao3

(1School of Psychology, Liaoning Normal University, Dalian 116029, China)(2School of Psychology, Shenzhen University, Shenzhen 518060, China)(3School of Education, Jianghan University, Wuhan 430056, China)

Previous experimental results have shown that worked-example learning can promote the solution of near, but not far, transfer problems. However, according to Sweller, in order to promote the solution of the far transfer problem, it was necessary to learn a series of worked-examples of variant problems solutions. Furthermore, they must try to solve problems requiring variant rules. Thus, they will be assigned a large number of homework exercises. To avoid this, we developed a rule worked-example learning method to promote far transfer problem solving, in which students applied rules variant reasoning after prototype worked-example learning. We carried out four experiments to test the effectiveness of this method.

In Experiment 1, 162 fourth-grade students were selected as participants. They were randomly divided into three groups. After learning the prototype worked-examples, the first group learned worked-examples of the four variant problem solutions. The second group applied rule variant reasoning to four problems presented to them. The third group solved four near transfer problems. Then, participants in all groups were evaluated by transfer tests. In Experiment 2, 54 mathematics high-performing students, 54 mathematics middle-performing students, and 54 mathematics low-performing students were selected as participants. After learning the prototype worked-examples, they all applied rule variant reasoning to four variant problems presented to them. Then, they all took transfer tests. In Experiment 3, 90 mathematics middle-performing students were randomly divided into three groups. Additionally, 90 mathematics low-performing students were randomly divided into three groups. After prototype worked-examples learning, two first groups made up the variant problems by self, and then they carried out rules variant reasoning for the variant problems; two second groups carried out rules variant reasoning for four variant problems presented to them; two third groups made four types division for eight variant problems presented to them, and then they carried out rules variant reasoning for the four kinds of the variant problems. Finally, they were all tested by transfer tests. In Experiment 4, 80 mathematics low-performing students were randomly divided into two groups. After learning prototype worked-examples, they all made four types division for eight variant problems presented to them. The first group carried out rules variant reasoning for the four kinds of the variant problems. The second group carried out rules variant reasoning using the variant problems of incomplete solving rules. Finally, they all took transfer tests.

The results showed that (1) The far transfer scores of the first group were significantly better than those of the second and the third groups, and that the second group’s scores were significantly better than those of the third group; (2) Significant differences were found in the far transfer test scores among three math performance levels; (3) The far transfer test scores of the third group were significantly better than those of the first and second groups; (4) The far transfer test scores of the second group were significantly better than those of the first.

It can be concluded that rule variant reasoning after learning prototype worked-example significantly promotes far transfer problem solving.

rule worked-example learning, variant problems, rule variant reasoning, variant rules, far transfer problems

2021-10-27

* 国家自然科学基金青年项目(31600912), 广东省哲学社会科学“十三五”规划项目(GD20CXL06), 深圳市科技创新委深圳市高等院校稳定支持计划面上项目(20200813121341001)。

张笑笑, E-mail: Zhangxx@szu.edu.cn; 高超, E-mail: gaochao_psy@foxmail.com

B849: G44