认知诊断模型Q矩阵修正:完整信息矩阵的作用*
2023-01-04刘彦楼吴琼琼
刘彦楼 吴琼琼
认知诊断模型Q矩阵修正:完整信息矩阵的作用*
刘彦楼1吴琼琼2
(1曲阜师范大学教育大数据研究院;2曲阜师范大学心理学院, 山东 济宁 273165)
Q矩阵是CDM的核心元素之一, 反映了测验的内部结构和内容设计, 通常由领域专家根据经验进行主观界定, 因此需要对可能存在的错误进行修正。本研究提出了一种新的Q矩阵修正方法——基于完整经验交叉相乘信息矩阵的Wald-XPD方法。采用Monte Carlo模拟检验了新方法的表现, 并与同类方法进行了比较。研究表明:新开发的Wald-XPD方法在Q矩阵恢复率、保留正确标定属性的比例以及修正错误标定属性的比例这3个主要指标上均有较好的表现, 且整体上优于其他方法, 尤其是在修正错误标定的属性方面。通过实证数据展示了Wald-XPD方法在Q矩阵修正中的良好表现。总之, 本研究为Q矩阵修正提供了有效的方法。
认知诊断模型, Q矩阵, XPD矩阵, Wald检验
1 引言
经典心理测量理论及项目反应理论采用单一的测验分数来描述被试在某个阶段的学习效果。作为新一代心理测量理论, 认知诊断(cognitive diagnosis)的主要目的是提供关于被试的多维、细粒度潜在特质(如知识、认识过程、技能、策略、人格特质或心理障碍等, 统称为属性)的诊断性评价信息, 认知诊断模型(cognitive diagnostic model, CDM)是研究者为了实现以上主要目的而提出的一类离散潜变量模型(Rupp et al., 2010)。目前, CDM已广泛应用于心理、教育、精神病理学等领域(Sorrel et al., 2016)。
Q矩阵是CDM的核心元素之一, 定义了测验所测属性与项目之间的对应关系(Tatsuoka, 1990), 它不仅决定着测验的内部结构, 也关系到认知诊断结果的准确性。正确设定的Q矩阵是获得准确的模型参数估计和被试分类的关键因素(Nájera et al., 2020), 错误设定的Q矩阵会产生很多不良的影响, 如降低模型参数估计准确性、导致较差的模型−数据拟合、导致错误的属性估计和被试分类等(Chiu, 2013; de la Torre, 2009; Rupp & Templin, 2008)。CDM中获取Q矩阵的方法主要是由领域专家根据经验构建(Sorrel et al., 2016), 但这种方法包含一定的主观性。实践中, 原始Q矩阵有较大可能包含一些错误设定(Rupp & Templin, 2008), 如何修正原始Q矩阵中可能存在的错误是研究者面临的重要理论与现实问题。

在饱和CDM框架下开发的以上8种参数化Q矩阵修正方法中, 残差方法对于属性过度设定不敏感且在测验长度较短时统计检验力可能会偏低; 当样本量较小时, TLP方法会高估错误设定项目的数量且用于减少错误报告率的重抽样校正方法(bootstrap bagging method)的耗时可能会特别长; 模拟研究表明iGDI的表现与iJSD的表现相当、甚至在一些条件下优于iJSD (Terzi, 2017); 相对拟合统计量方法需要比较测验的所有项目关于属性所有可能组合的相对拟合值, 尽管研究者提出一些减少计算次数的方法, 但是在测验长度较长或属性数量较多的情况下, 计算耗时仍有可能特别长。GDI在饱和CDM框架下采用单个项目所有可能的属性掌握模式中正确答对概率的方差来衡量Q矩阵中相对应的q向量的区分能力, 选择有最大区分能力的q向量作为正确设定的q向量。相对于GDI而言, iGDI的估计效果有了一定程度的改善, 但是这类方法的主要缺点是需要人为地确定一个截止值(Nájera et al., 2019)。以GDI研究为基础, Ma和de la Torre (2020)将Q矩阵修正的视角延伸到多级计分模型, 在seq-GDINA模型(the sequential GDINA model; Ma & de la Torre, 2016)下提出了GDI和基于不完整信息矩阵的Wald检验相结合的Wald-IC方法。Wald-IC方法首先采用GDI方法从单一属性的q向量中确定第一个所需属性, 再逐步多次采用Wald统计量决定是否增加或删除属性来选择恰当的q向量。即, 在单个项目上Wald-IC仅需执行− 1个统计检验即可完成。Hull方法试图在模型拟合与简约之间找到一种平衡以此选择恰当的q向量, 研究者(Nájera et al., 2021)通过模拟研究比较了GDI、Wald-IC以及Hull方法, 结果表明在大多数条件下Hull的表现最好、Wald-IC的表现稍逊于Hull。但是, Hull和Wald-IC在修正错误标定的属性方面的表现较差, 尤其是Q矩阵中存在较多错误设定时。研究者(Ma & de la Torre, 2020; Nájera et al., 2021)构建的Wald-IC统计量是使用不完整信息矩阵计算的。先前研究表明, 采用不完整信息矩阵构建的统计量在后续研究中会导致一些问题, 如低估模型参数标准误(Philipp et al., 2018)、用于项目功能差异检验及项目水平模型比较时导致一类错误控制率膨胀(Liu, Andersson, et al., 2019; Liu, Yin, et al., 2019; 刘彦楼等, 2016)等。基于此, 本研究认为Wald-IC方法在修正错误标定属性方面表现较差的主要原因可能是在Wald统计量的计算中采用了不完整的信息矩阵。
研究者(Liu et al., 2016; Liu, Xin, et al., 2019; Liu et al., 2021; Philipp et al., 2018; 刘彦楼等, 2016)认为CDM中同时存在两种类型的模型参数:项目参数和结构参数。不完整信息矩阵(de la Torre, 2009; 2011)忽略了结构参数, 计算量较小, 有较大可能导致Q矩阵修正结果不够准确。以往研究者提出了多种完整信息矩阵估计方法(Liu, Xin, et al., 2019; Liu et al., 2021; Philipp et al., 2018; 刘彦楼等, 2016), 但是这些关于模型参数的信息矩阵无法直接用于Q矩阵修正中Wald统计量的计算, 因为此类Wald统计量中使用的是关于模型参数的方差−协方差矩阵。此外, 与其他完整信息矩阵相比, 经验交叉相乘信息矩阵(empirical cross-product informationmatrix, XPD; Liu et al., 2021; Philipp et al., 2018; 刘彦楼等, 2016)计算量较小, 故本研究在包含全部模型参数的XPD矩阵的基础上, 经过转换获得关于项目正确作答概率的方差−协方差矩阵, 以此构建用于Q矩阵修正的Wald统计量(记为Wald-XPD)。
本文的主要目的在于提出一种新的Q矩阵修正方法, 并通过模拟研究与实证数据分析考察新方法的表现。模拟研究参考了以往研究者研究中采用的模拟条件(de la Torre & Chiu, 2016; Ma & de la Torre, 2020; Nájera et al., 2021), 考察新开发的方法在Q矩阵修正中的表现, 并与同类方法进行比较, 希望能够为实践研究者在Q矩阵修正方法的选用方面提供方法支持。本研究选择GDI、Hull、Wald-IC方法与Wald-XPD方法进行比较的原因是:首先, Wald-XPD是在Wald-IC方法基础上提出的, 新方法与旧方法表现的异同有待探索; 其次, 先前研究表明在GDI、Hull、Wald-IC三种方法中, Hull的表现是最好的, 故有必要比较Hull与Wald-XPD两种方法的表现; 第三, 限制GDI及iGDI方法实践应用的主要原因是这两种方法均需要人为地设置一个截止值, 与iGDI相比, 固定的截止值对GDI方法的影响相对较小(Nájera et al., 2020), 因此本研究将GDI也纳入比较。本文的第二部分介绍了以往研究者在饱和的CDM框架下提出的参数化Q矩阵修正方法。第三部分介绍了新开发的Wald-XPD方法。第四部分采用模拟研究, 在较广泛和真实的条件下探索Wald-XPD方法的具体表现, 并与GDI、Hull以及Wald-IC方法进行比较。第五部分探讨Wald-XPD方法在实证数据分析中的应用, 并与Hull方法、Wald-IC方法进行比较。最后对Wald-XPD方法进行了讨论与展望。
2 饱和CDM框架下的参数化Q矩阵修正方法



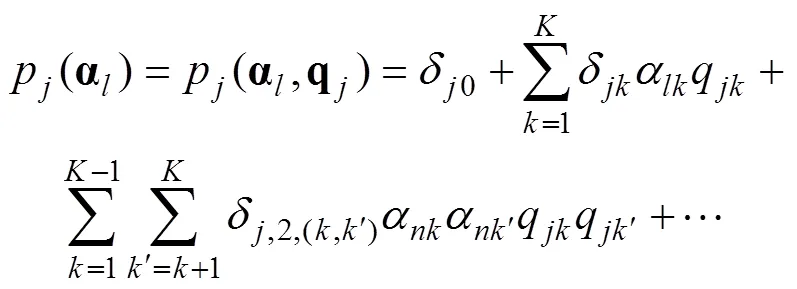
2.1 GDI方法




截止值用来判断一个q向量的PVAF是否合适。一个正确设定的q向量需要满足两个条件:(1)PVAF大于截止值; (2)包含的属性数最少。若多个q向量同时满足以上两个条件, 则选择PVAF值最大的q向量作为正确设定的q向量。
2.2 Hull方法
Hull方法(Nájera et al., 2021)的基本原理是:在项目水平上比较所有可能q向量的拟合指标。将所有可能的q向量呈现在Hull图上, Hull图的横坐标表示与每个q向量相关的参数数量, 纵坐标表示拟合指标。Hull方法选取的拟合指标有两个:第一个是PVAF, 用来评估不同q向量的项目区分度大小; 第二个是绝对模型拟合指McFadden pseudo-2(McFadden, 1974), 用于衡量观察反应中方差所占的比例, 评估获得的估计值与观察反应之间的拟合度(Hull方法的两个指标在下文分别表示为HullP和HullR)。选择项目中不同参数数量下有最大PVAF或McFadden pseudo-2值的q向量作为候选q向量, 任意两个候选q向量之间会形成一条线段, 将该线段下方的所有q向量移除, 故Hull图成一条单调递增的曲线。假设项目的= 3, 那么以PVAF为指标的Hull图如图1所示, 图中上方蓝色字体表示候选q向量, 下方黑色字体表示该候选q向量的PVAF。

图1 K = 3时, 以PVAF为指标的Hull图
对于Hull方法的两个拟合指标而言, 添加项目中相关联的属性会显著增加拟合指标的值; 添加不关联的属性也会增加拟合指标的值, 但影响可能较小。故从拟合−简约相平衡的视角出发, 在Hull图中选择先使拟合指标显著增加, 然后使拟合指标平缓增加的候选q向量作为正确设定的q向量。基于此, 研究者采用指数(Ceulemans & Kiers, 2006)计算每个候选q向量的拐角大小(the magnitude of the elbow), 选择指数最大的候选q向量作为正确设定的q向量:


2.3 Wald-IC方法
用于Q矩阵修正的Wald统计量也是在项目水平上进行的, 其基本原理是:假设项目所对应的q向量定义了2个及以上的属性, 如果将某一属性从q向量中移除而没有导致模型−数据拟合变差, 那么这个属性就不是必需的。为便于理解, 现举例说明。假设一个测验共测量了2个属性, 即= 2, 那么, 所有可能的属性掌握模式有4种, 可以表示为:




Wald-IC统计量的形式为:



3 基于完整XPD矩阵的Wald-XPD方法
3.1 使用XPD矩阵构建Wald-XPD统计量


在构建Wald统计量之前, 本研究首先对XPD矩阵做了以下三个方面的处理:



(3)对比完整和不完整信息矩阵可知, 完整信息矩阵考虑模型中的全部参数, 计算量较大, 修正过程较为耗时。故本研究采用C++语言编写XPD矩阵, 提高Q矩阵修正的速度。
3.2 Wald-XPD方法的具体实施步骤

本研究新提出的Wald-XPD方法的修正步骤如下:
步骤(1):选择项目中具有最大PVAF值的单一属性q向量中包含的属性为第一个所需属性, 更新集合A、B。
步骤(2):将该单一属性q向量的PVAF值与0.95进行比较, 大于0.95说明该q向量是合适的, 停止修正, 否则继续修正。
步骤(3):更新集合A、B。选出具有较大PVAF的q向量进行修正, 将该q向量中各属性使用Wald-XPD统计量进行显著性检验, 确定该q向量对应的集合A和集合B中的属性是否应该移除或添加, 然后判断q向量的PVAF是否大于0.95, 大于0.95说明这个q向量是合适的, 停止修正, 否则继续修正。
步骤(4):重复步骤(3), 直到某个q向量的PAVF值大于0.95, 或者没有属性移除或添加则停止修正。
步骤(5):在单个项目修正结束后, 重新计算PVAF以及Wald-XPD统计量, 直到达到最大迭代或者某次迭代结束后的q向量与前一次迭代的q向量完全相等则停止修正。
为了便于理解, 现举例说明Wald-XPD方法用于某个项目的q向量的修正算法。假设项目中q向量的属性数= 3, Wald-XPD方法修正该q向量的过程如图2所示。
4 模拟研究
模拟研究的目的是在较为广泛和真实的条件下探讨Wald-XPD方法在Q矩阵修正中的表现, 并与以往研究者提出的GDI、Wald-IC以及Hull (HullP、HullR)方法进行比较。
4.1 方法
4.1.1 研究设计
为便于比较, 本研究参考以往研究设计(Ma & de la Torre, 2020; Nájera et al., 2021), 共操纵了5种因素:项目数和属性数的比例(ratio of number of items to attribute,)、样本量()、Q矩阵错误设定的比例(Q-matrix misspecification rate,)、属性分布(attribute distribution,)、项目质量(item quality,)。本研究将属性数设置为= 4, 因为这是应用类文章中最经常出现的属性数(Nájera et al., 2020)。以往研究中常用的项目数是11到30 (Sessoms & Henson, 2018), 故本研究将项目数设置为16和32, 所以, 本研究共考虑2种测验结构:= 16[(= 4)× (= 4)]、= 32[(= 4)×(= 8)]。样本量有两个水平:500和1000 (Chen, 2017; de la Torre, 2011; Ma & de la Torre, 2016), 分别代表小样本和大样本。本研究共有48个实验条件, 各因素水平如表1所示。

图2 Wald-XPD方法用于向量的修正流程图

表1 模拟研究中各因素水平汇总
4.1.2 数据生成

项目质量分为高、中、低3个水平。高项目质量:P(0) ~(0, 0.2)且P(1) ~(0.8, 1); 中等项目质量:P(0) ~(0.1, 0.3)且P(1) ~(0.7, 0.9); 低项目质量:P(0) ~(0.2, 0.4)且P(1) ~(0.6, 0.8)。其中,P(0)表示仅凭猜测答对的概率,P(1)表示掌握项目所要求的全部属性的被试答对该项目的概率。成功的概率有两种限制:(1)项目反应函数在属性数上具有单调性; (2)与单个属性相联系的项目参数的总和限制为大于0.15。这两个条件保证所有的属性都具有不可忽视的作用。
真实Q矩阵符合以下限制:(1)每个Q矩阵至少包含两个单位矩阵(identity matrix); (2)除了两个单位矩阵外, 每个项目至少测量一个属性; (3) Q矩阵由1个属性q向量(50%)、2个属性q向量(25%)和3个属性q向量(25%)组成。这个比例主要是参考之前研究(Nájera et al., 2021), 使用较高比例的单一属性q向量的原因是满足每个Q矩阵至少包含两个单位矩阵的模型可识别条件(Gu et al., 2018)。错误设定的Q矩阵的比例为:0.15和0.3。错误设定是在两个约束条件下随机引入:(1)所有项目必须至少测量一个属性; (2)始终保留一个单位矩阵。
在每个条件下, 均生成500个数据集, 每个数据集中生成新的真实Q矩阵和项目参数。所有的模拟研究和分析都在R软件中进行。
4.1.3 评价指标
QRR (Q-matrix recovery rate)用来测量Q矩阵的恢复比例, 可以表示为:

TPR (true positive rate)表示保留正确标定属性的比例:

TNR (true negative rate)表示修正错误标定属性的比例:

本研究除了使用QRR、TPR、TNR来考察各个方法总体的表现之外, 还参考其他指标来获得更加全面具体的结果。OS表示过度设定, US (under- specifications)表示吝啬设定, 表达式分别为:


以上5个指标从不同方面反映了Q矩阵的修正效果。其中, QRR、TPR、TNR的值越高, 表示该修正方法的Q矩阵恢复率以及保留正确标定属性和修正错误标定属性的比例越高, 修正效果越好。OS和US的值越小, 表示该修正方法存在较少过度设定和吝啬设定的趋势, 修正效果越好。
4.2 研究结果
4.2.1 GDI、Hull、Wald-IC以及Wald-XPD在各因素不同水平上的表现
表2呈现了GDI、Hull (HullP、HullR)、Wald-IC以及Wald-XPD方法在各因素不同水平上的QRR、TPR、TNR、OS和US值, 表中加粗数据是相同条件下的最优结果。
首先, 比较的是各实验条件的综合影响。Q矩阵错误设定的比例、项目质量、样本量以及属性分布对于GDI、Wald-IC、Hull (HullP、HullR)以及Wald-XPD方法在各个指标上的表现有明显影响。除Hull (HullP、HullR)方法的TPR指标受项目质量的影响较小外, 在项目质量较高的条件下, 所有方法的表现均优于其他水平。Q矩阵错误设定的比例和样本量对于4种方法在各个指标上的表现也存在一定的影响, 随着Q矩阵错误设定的比例降低和样本量增大, 4种方法均有更好的Q矩阵修正表现。均匀分布下, 4种方法在各个指标上的表现均优于高阶分布。就因素而言,对于GDI、Wald-IC和Wald-XPD在QRR指标上的表现, 以及所有的修正方法在TNR指标上的表现影响明显, 所有指标在= 8水平下的结果优于= 4。
其次, 比较的是4种修正方法的综合表现。所有方法在QRR以及TPR指标上没有表现出明显优劣。其中, 本研究中新提出的Wald-XPD在TNR指标上的表现明显优于其他方法; GDI在OS指标上的表现较优, 但是在US指标上表现相对较差; HullR在OS指标上的表现较差, 但是在US指标上表现相对较优; Wald-IC在US指标上表现相对较差。
根据以上综合比较可知, Wald-XPD以及HullP在各个指标上有相对较好的表现, 且在TNR指标上Wald-XPD的表现最好。此外, 鉴于Wald-XPD是在Wald-IC基础上新提出的方法, 故接下来本研究主要探讨Wald-XPD、Wald-IC以及HullP方法在QRR、TPR以及TNR这3个主要指标上的具体表现, 并重点关注Wald-XPD在TNR指标上的表现, 即Wald-XPD修正Q矩阵中错误标定属性的能力。
4.2.2 Wald-XPD在修正错误标定属性时的表现
图3呈现的是HullP、Wald-IC以及Wald-XPD方法在48种具体的模拟条件下获得的QRR的值。由图3可知, 项目质量对于这3种方法的表现影响最为明显, 随着项目质量的提高, QRR的值也在增加。另外, 样本量、Q矩阵错误设定的比例以及属性分布对于这3个方法在QRR指标上的表现稍有影响, 且趋势一致。就QRR指标而言, HullP、Wald-IC以及Wald-XPD方法的表现仅有细微差异, 即当= 0.4时Wald-XPD的表现略微低于另外两种方法。
图4呈现的是3种方法在TPR指标上的表现。由图4可知, 在所有条件下Wald-IC以及HullP方法均能获得较高的TPR值。项目质量对于Wald- XPD方法的表现有一定的影响, 当项目质量较低时, Wald-XPD在TPR指标上的表现不如Wald-IC以及HullP方法; 随着项目质量的提高, 3种方法在TPR指标上的表现相当。

表2 不同因素水平的结果
注:粗体表示各指标不同水平下的最好结果。

图3 HullP、Wald-IC与Wald-XPD方法在QRR指标上的表现

图4 HullP、Wald-IC与Wald-XPD方法在TPR指标上的表现
图5呈现的是3种方法在TNR指标上的表现。在所有条件下, Wald-XPD方法在TNR指标上的表现均是最优的, 对比Wald-XPD方法在TPR及TNR上的表现可知, 低项目质量条件对这个方法产生了一些不利影响, 而在中等或高项目质量条件下, Wald-XPD能有效保留Q矩阵中正确标定的属性, 也能有效修正Q矩阵中错误标定的属性。测验长度较短、项目质量较低及Q矩阵错误设定比例较高时HullP方法的表现较差, 结合同样条件下HullP在TPR指标上的表现可知, 虽然HullP方法在保留正确标定属性方面略微优于Wald-XPD, 但是它较多地保留了错误标定的属性。即, HullP方法倾向于较少地修正原始Q矩阵中的属性。在低项目质量条件下的多数情景中, 虽然Wald-IC方法在TNR上的表现优于HullP, 但是在随着项目质量的提高HullP在多数情景中的表现优于Wald-IC。HullP、Wald-IC以及Wald-XPD方法在TNR指标上的表现受样本量、测验长度、项目质量、属性分布及错误设定比例的影响明显。随着Q矩阵错误设定比例降低、项目质量提高、测验长度增加, HullP和Wald-IC方法的TNR值有所提高, 但仍低于Wald-XPD方法的TNR值。

图5 HullP、Wald-IC与Wald-XPD方法在TNR指标上的表现
5 实证数据分析

本研究在饱和G-DINA模型框架下, 使用HullP、Wald-IC以及Wald-XPD方法对原始Q矩阵进行了修正。表3中的结果显示, HullP方法共修正了6个元素, Wald-IC方法共修正了5个元素, Wald-XPD方法一共修正了16个元素, Wald-IC方法修正的5个元素均包括在Wald-XPD方法修正的元素之中。使用相对拟合、绝对拟合及近似拟合指标比较原始Q矩阵、HullP、Wald-IC及Wald-XPD方法修正后的Q矩阵的模型−数据拟合表现。拟合指标包括:相对拟合指标AIC (Akaike information criterion)和BIC (Bayesian information criterion)、有限信息绝对拟合(limited-information absolute fit)指标2及近似拟合指标RMSEA2(root mean square error of approximation; Liu et al., 2016), 结果见表4。就相对拟合指标而言, QHullP获得最佳的AIC指标, QXPD的AIC指标与其接近; QXPD获得最佳的BIC指标, 其次是QIC, QHullP的BIC指标最差。即, Wald-XPD方法修正后的Q矩阵的相对拟合指标更优。在绝对拟合指标2上, QIC的< 0.01, 表明Wald-IC方法修正的Q矩阵与数据失拟; QHullP和QXPD的值分别为:0.029和0.019, 表明HullP和Wald-XPD方法修正后的Q矩阵没有在0.01显著性水平上拒绝模型−数据拟合的原假设。对于RMSEA2指标而言, 其值越接近0修正效果越好, 其中QXPD的RMSEA2最接近于0, 即QXPD在RMSEA2指标上有最好的表现(Liu et al., 2016)。综合考虑相对拟合、绝对拟合和近似拟合指标, 本研究认为Wald-XPD方法修正后的Q矩阵在模型−数据拟合方面表现最优。
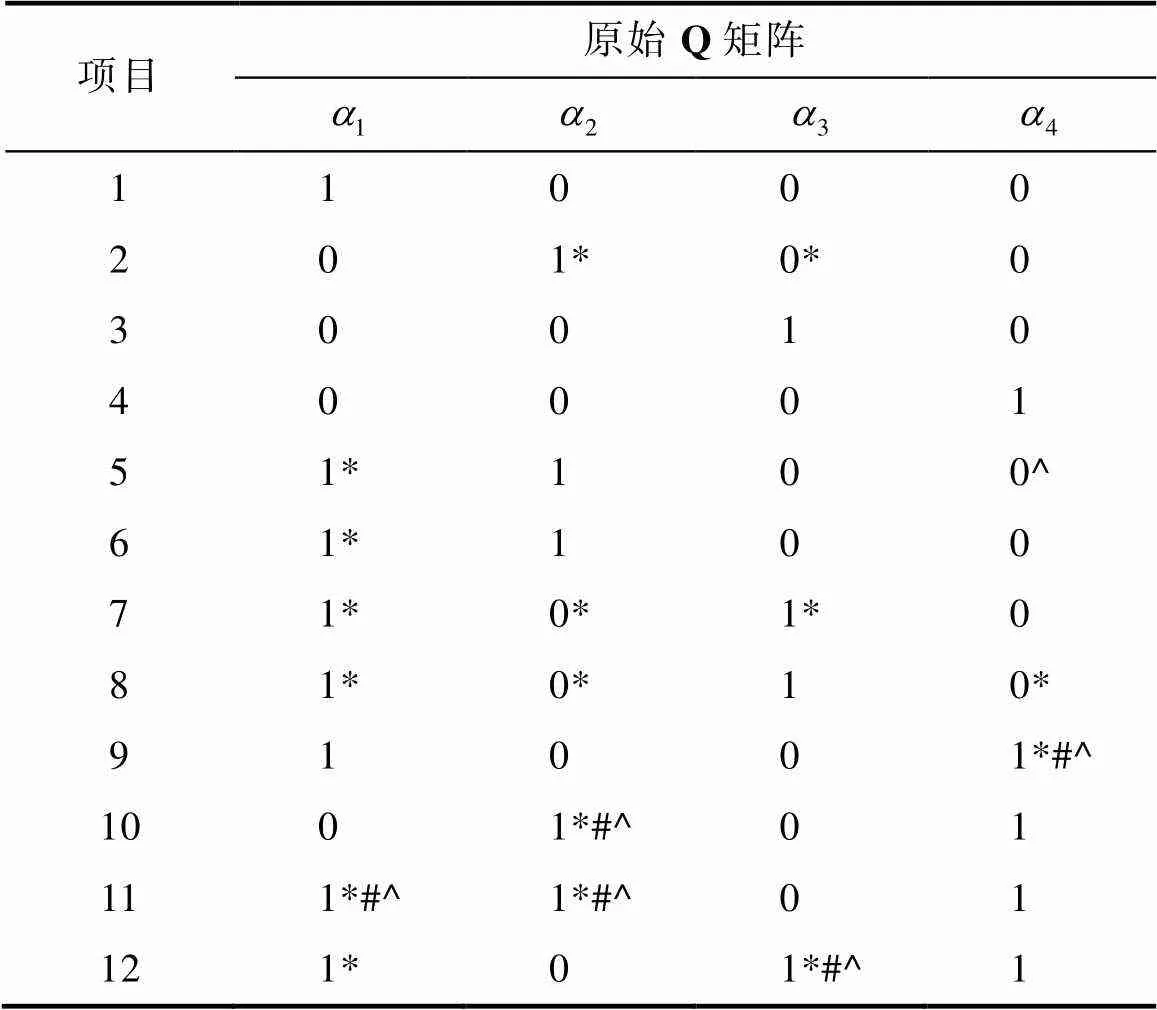
表3 原始Q矩阵以及各方法对属性的修正情况
注:*为Wald-XPD方法调整的属性, #为Wald-IC方法调整的属性, ^为HullP方法调整的属性
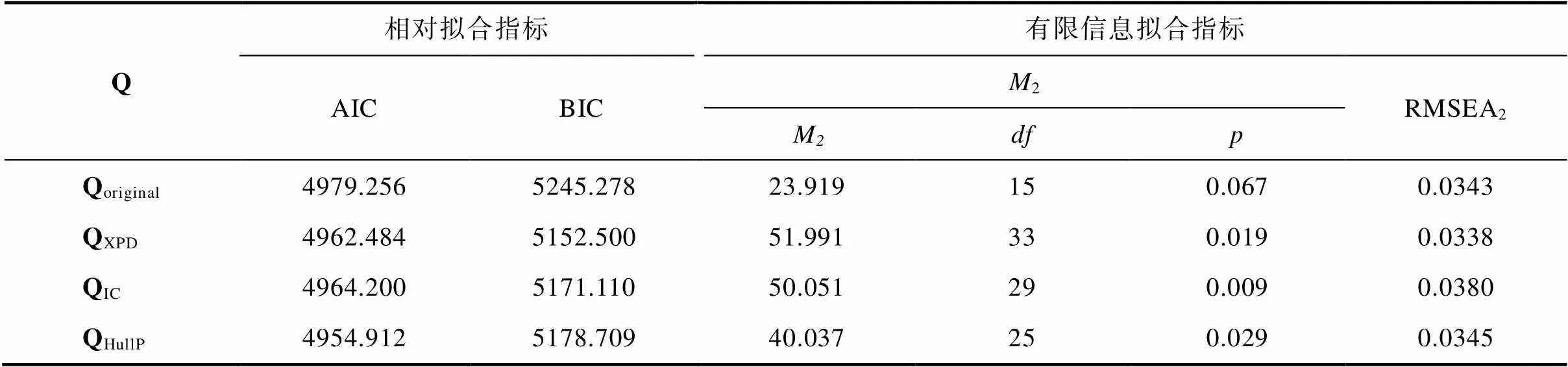
表4 基于3种方法修正前后Q矩阵的拟合指标
需要特别说明的是, 本研究的目的是在一般性的CDM框架下开发具有广泛适用性的Q矩阵修正方法。因此, 实证数据分析的重点是原始Q矩阵的修正, 没有在饱和G-DINA模型的基础上进一步在项目水平上进行模型比较(Liu, Andersson, et al., 2019)。另外,2统计量在模型参数过度设定时, 即模型中冗余参数过多时, 可能存在统计检验力不足的问题(参考Chen et al., 2018)。举例而言, 对比原始Qoriginal矩阵及修正后的QXPD矩阵可知, Qoriginal中可能存在较多过度设定的元素, 因此, 导致Qoriginal的2统计量的值大于0.01。参考先前研究(Liu et al., 2016), 本文认为在模型−数据拟合评价方面, 近似拟合统计量RMSEA2可能更具参考价值。

值得注意的是, 本研究中提出的Q矩阵修正方法是从作答数据出发的, 在一定程度上可以避免专家标定Q矩阵的主观性, 减轻专家负担, 但是客观方法标定的Q矩阵不能直接作为最终的Q矩阵, 应该作为专家标定Q矩阵的重要参考(Xu & Shang, 2018)。
6 讨论与展望
6.1 结论与讨论
CDM依赖正确设定的Q矩阵以获得准确的属性剖面分类(Rupp & Templin, 2008)。以往研究者提出的GDI、Wald-IC、Hull方法在多数的应用情景中虽然有较好的表现, 但这些方法对Q矩阵中错误标定的属性不够敏感。本研究提出使用完整的XPD矩阵计算用于Q矩阵修正的方法(Wald-XPD方法), 并系统探讨了样本量、测验长度、Q矩阵错误设定比例、属性分布等因素对Q矩阵修正结果的影响。采用实证数据展示了新提出的Wald-XPD方法在实际应用中的表现与价值。
本研究结果表明:(1)整体而言, Wald-XPD方法的表现优于GDI、Hull、Wald-IC方法。Wald-XPD方法能够弥补GDI、Hull、Wald-IC方法在一些条件下对于错误标定属性不敏感的不足之处, 且在Q矩阵恢复率和保留正确标定属性的比例方面也有较好的表现。(2) GDI、Hull、Wald-IC和Wald-XPD方法随着项目质量的提高、样本量增大、测验长度增加以及Q矩阵错误设定比例的降低, 在修正Q矩阵上有更好的表现。(3)由HullP、Wald-IC以及Wald-XPD方法进一步比较的结果可知, 3种方法在Q矩阵恢复率方面差异较小, HullP、Wald-IC在保留正确标定的属性方面的表现略优于Wald-XPD方法, 但在所有模拟条件下, Wald-XPD方法在修正错误标定的属性方面的表现均优于另外两种方法。(4)实证数据分析的结果表明, Wald-XPD方法修正后的Q矩阵与原始数据有最优的拟合度。
在本研究操纵的5种因素中, 项目质量对GDI、Hull、Wald-IC、Wald-XPD方法表现的影响较大, 样本量和测验长度也对4种修正方法的表现有一定的影响。出现这种现象的原因可能是, 项目质量越高、样本量越大以及测验长度越长, 被试观察作答反应矩阵中包含的关于CDM中未知参数的信息越多, 因此, 以上4种方法的表现也就越好。与以往研究类似(Kang et al., 2019; Ma & de la Torre, 2020; Nájera et al., 2021), 本研究同样认为属性分布对于GDI、Hull、Wald-IC、Wald-XPD方法在TNR指标上的表现有细微的影响。出现这种现象的原因可能是, 当属性服从均匀分布时所有可能属性掌握模式分布的概率是相等的, 即被试观察作答反应矩阵中包含的关于结构参数的信息是一样的。当属性服从高阶分布时, 属性之间存在一定的关联性, 使某些属性掌握模式分布的概率可能会比较高, 另外一些属性掌握模式分布的概率会比较低, 故被试观察作答反应矩阵中包含的结构参数的信息量较少。于是, 当属性服从均匀分布时, 4种方法在各个指标上的表现略优。Q矩阵错误设定的比例对GDI、Wald-IC、Hull方法表现的影响较大, 随着Q矩阵错误设定比例的降低, 它们能够获得更高的QRR、TPR和TNR值, 这与已有研究结果一致(Ma & de la Torre, 2020; Nájera et al., 2021)。然而, Q矩阵错误设定的比例对Wald-XPD方法表现的影响则相对较小, 结合Wald-XPD在TNR指标上的表现, 本研究认为可能是Wald-XPD在迭代结束前的循环中能够有效修正Q矩阵错误标定的属性。
此外, 研究结果表明, Wald-XPD方法在TPR和TNR指标上与Wald-IC、HullP方法的表现不同。在TPR指标上, Wald-XPD受项目质量低的影响明显, 在TNR指标上, Wald-IC和HullP受项目质量低以及测验长度短这两种因素的影响明显。TPR指标数值低, 说明Q矩阵修正方法倾向于修改正确标定的属性, TNR数值低则说明Q矩阵修正方法修改错误标定属性的能力弱。综合TPR、TNR两个指标可知, 虽然Wald-XPD方法在项目质量较低的条件下能够较为有效地修正错误标定的属性, 但是存在过度修改正确标定属性的倾向。换言之, Wald-XPD方法虽然提高了Q矩阵修正的表现, 但是在项目质量较低的条件下, 有可能会错误地修正了正确标定的元素。Wald-IC以及HullP虽然在项目质量较低的条件下不存在过度修改正确标定属性的倾向, 但却无法有效修正错误标定的属性, 尤其是HullP方法。所以, 本研究建议使用Q矩阵修正方法时, 需要注意项目质量, 若项目质量较低, 可以结合多种修正方法、参考专家意见进而获得准确的Q矩阵。
本研究采用C++语言编写XPD矩阵, 在一定程度上能够提高Q矩阵修正的速度, 但是, 由于Wald-XPD方法考虑模型中的全部参数且采用迭代的方式进行, 在一些条件下可能耗时较长。例如, Wald-XPD方法最短的平均用时是12.50 s, 最长的平均时间需要746.01 s。Wald-XPD方法在各个模拟条件下的平均运行时间见表5。
6.2 研究展望
本研究提出的Wald-XPD方法在Q矩阵修正中有较好的表现, 但仍存在一些不足之处, 值得后续研究者进一步探讨。(1)虽然Wald-XPD统计量有明确的渐近分布(χ2分布), 不需要像GDI类方法那样人为地确定一个截止值, 但限于研究目的和篇幅本文仅在0.05显著性水平上对于Wald-XPD统计量的表现进行了显著性检验, 未来研究者可以进一步探讨不同的显著性水平对于Wald-XPD统计量表现的影响。(2)本研究仅以完整信息矩阵中的XPD矩阵构建Wald统计量进行Q矩阵修正, 除了XPD矩阵之外, 研究者还可以将其他完整信息矩阵构建的Wald统计量用于Q矩阵修正, 如Liu等人(2021)提出改进的观察信息矩阵以及三明治信息矩阵。不同类型的完整信息矩阵构建的Wald统计量在Q矩阵修正中的表现也值得进一步研究。(3)本研究仅在G-DINA模型下对Q矩阵修正方法进行了对比研究, G-DINA模型适用于0-1计分的测验情景, 但在心理与教育测验中存在较多的多级计分数据。研究者们开发了很多能用于多级计分的CDM, 如多级计分GDM (von Davier, 2008), 研究者可以将Wald- XPD方法拓展到多级计分模型中, 并考察其在多级计分模型中的表现。(4)本研究在考察新提出的Wald-XPD方法的表现时, 仅与一次修正的GDI、Wald-IC方法进行了比较, 研究者也认为GDI、Wald-IC方法可以迭代进行, 如迭代GDI方法(Nájera et al., 2020)。此外, 还有其他迭代修正的方法, 如迭代修正序列搜索(Terzi & de la Torre, 2018)等, 研究者也可以尝试将这些方法与Wald-XPD方法进行比较。(5) Wang等人(2020)评估了在Q矩阵部分已知的情况下, GDI和Wald-IC方法在估计新项目的q向量中的表现。基于此, 未来研究者可以在Q矩阵部分已知的情况下进一步评估Wald-XPD方法估计Q矩阵的表现, 并与已有的Q矩阵估计方法, 如ICC-IR方法(汪大勋, 高旭亮, 蔡艳等, 2018)、似然比D2方法(喻晓锋等, 2015)、非参数Q矩阵校准(Lim & Drasgow, 2017)、两阶段搜索算法(Feng, 2013)、似然比检验(Wang et al., 2020)等方法进行比较。

表5 Wald-XPD方法在各模拟条件下的平均运行时间(s)
注:*为Wald-XPD方法在模拟条件下的最长运行时间, #为Wald-XPD方法在模拟条件下的最短运行时间。
Chen, F., Liu, Y., Xin, T., & Cui, Y. (2018). Applying theMstatistic to evaluate the fit of diagnostic classification models in the presence of attribute hierarchies., Article 1875.
Chen, J. (2017). A residual-based approach to validate Q-matrix specifications.(4), 277–293.
Chiu, C.-Y. (2013). Statistical refinement of the Q-matrix in cognitive diagnosis.(8), 598–618.
De la Torre, J. (2008). An empirically based method of Q-matrix validation for the DINA model: Development and applications.(4), 343–362.
De la Torre, J. (2009). DINA model and parameter estimation: A didactic.(1), 115–130.
De la Torre, J. (2011). The generalized DINA model framework.(2), 179–199.
De la Torre, J., & Chiu, C.-Y. (2016). A general method of empirical Q-matrix validation.(2), 253–273.
De la Torre, J., & Douglas, J. A. (2004). Higher-order latent trait models for cognitive diagnosis.(3), 333–353.
Feng, Y. (2013).(Unpublished doctoral dissertation). University of South Carolina, Los Angeles, America.
Gu, Y., Liu, J., Xu, G., & Ying, Z. (2018). Hypothesis testing of the Q-matrix.(3), 515–537.
Heller, J., & Wickelmaier, F. (2013). Minimum discrepancy estimation in probabilistic knowledge structures., 49–56.
Kang, C. H., Yang, Y. K., & Zeng, P. H. (2019). Q-matrix refinement based on item fit statistic RMSEA.(7), 527–542.
Li, J., Mao, X., & Wei, J. (2022).A simple and effective new method of Q-matrix validation.(8), 996–1008.
[李佳, 毛秀珍, 韦嘉. (2022).一种简单有效的Q矩阵修正新方法.(8), 996–1008.]
Li, J., Mao, X., & Zhang, X. (2021).Q-matrix estimation (validation) methods for cognitive diagnosis.(12), 2272–2280.
[李佳, 毛秀珍, 张雪琴. (2021). 认知诊断Q矩阵估计(修正)方法.(12), 2272–2280.]
Li, X., & Wang, W. (2015). Assessment of differential item functioning under cognitive diagnosis models: The DINA model example.(1), 28–54.
Lim, Y., & Drasgow, F. (2017). Nonparametric calibration of item-by-attribute matrix in cognitive diagnosis.(5), 562–575.
Liu, J., Xu, G., & Ying, Z. (2012). Data-driven learning of Q-matrix.(7), 548–564.
Liu, Y., Andersson, B., Xin, T., Zhang, H., & Wang, L. (2019). Improved Wald statistics for item-level model comparison in diagnostic classification models.,(5), 402–414.
Liu, Y., Tian, W., & Xin, T. (2016). An application of2statistic to evaluate the fit of cognitive diagnostic models.(1), 3–26.
Liu, Y., Xin, T., Andersson, B., & Tian, W. (2019). Information matrix estimation procedures for cognitive diagnostic models.(1), 18–37.
Liu, Y., Xin, T., & Jiang, Y. (2021). Structural parameter standard error estimation method in diagnostic classificationmodels: Estimation and application.Advance online publication. https://doi.org/ 10.1080/00273171.2021.1919048
Liu, Y., Xin, T., Li, L., Tian, W., & Liu, X. (2016). An improved method for differential item functioning detection in cognitive diagnosis models: An application of Wald statistic based on observed information matrix.(5), 588–598.
[刘彦楼, 辛涛, 李令青, 田伟, 刘笑笑. (2016). 改进的认知诊断模型项目功能差异检验方法——基于观察信息矩阵的Wald统计量.(5), 588–598.]
Ma, W., & de la Torre, J. (2016). A sequential cognitive diagnosis model for polytomous responses.(3), 253–275.
Ma, W., & de la Torre, J. (2020). An empirical Q-matrix validation method for the sequential generalized DINA model.(1), 142–163.
McFadden, D. (1974). Conditional logit analysis of qualitative choice behavior. In P. Zarembka (Ed.),(pp. 105–142). New York, NY: Academic Press.
Nájera, P., Sorrel, M. A., & Abad, F. J. (2019). Reconsidering cutoff points in the general method of empirical Q-matrix validation.(4), 727–753.
Nájera, P., Sorrel, M. A., de la Torre, J., & Abad, F. J. (2020). Improving robustness in Q-Matrix validation using an iterative and dynamic procedure.(6), 431–446.
Nájera, P., Sorrel, M. A., de la Torre, J., & Abad, F. J. (2021). Balancing fit and parsimony to improve Q-matrix validation.B(Suppl 1), 110–130.
Philipp, M., Strobl, C., de la Torre, J., & Zeileis, A. (2018). On the estimation of standard errors in cognitive diagnosis models.(1), 88–115.
Rupp, A. A., & Templin, J. (2008). The effects of Q-matrix misspecification on parameter estimates and classification accuracy in the DINA model.(1), 78–96.
Rupp, A. A., Templin, J., & Henson, R. A. (2010).. Guilford.
Sessoms, J., & Henson, R. A. (2018). Applications of diagnostic classification models: A literature review and critical commentary.(1), 1–17.
Sorrel, M. A., Olea, J., Abad, F. J., de la Torre, J., Aguado, D., & Lievens, F. (2016). Validity and reliability of situational judgement test scores: A new approach based on cognitive diagnosis models.(3), 506–532.
Tatsuoka, K. K. (1990). Toward an integration of item-response theory and cognitive error diagnosis. In N. Frederiksen, R. Glaser, A. Lesgold, & M. Shafto (Eds.),(pp. 453–488). Hillsdale, NJ: Erlbaum.
Terzi, R. (2017).(Unpublished doctoral dissertation).The State University of New Jersey, New Brunswick, America.
Terzi, R., & de la Torre, J. (2018). An iterative method for empirically-based Q-matrix validation.(2), 248–262.
Tu, D., Cai, Y., & Dai, H. (2012). A new method of Q-Matrix validation based on DINA model.(4), 558–568.
[涂冬波, 蔡艳, 戴海琦. (2012). 基于DINA模型的Q矩阵修正方法.(4), 558–568.]
von Davier, M. (2008). A general diagnostic model applied to language testing data.(2), 287–307.
Wang, D., Cai, Y., & Tu, D. (2020). Q-matrix estimation methods for cognitive diagnosis models: Based on partial known Q-matrix.Advance online publication. https://doi.org/10.1080/ 00273171.2020.1746901
Wang, D., Gao, X., Cai, Y., & Tu, D. (2018). A new Q-matrix estimation method: ICC based on ideal response.(2), 466–474.
[汪大勋, 高旭亮, 蔡艳, 涂冬波. (2018). 一种非参数化的Q矩阵估计方法: ICC-IR方法开发.(2), 466–474.]
Wang, D., Gao, X., Cai, Y., & Tu, D. (2020).A method of Q-matrix validation for polytomous response cognitive diagnosis model based on relative fit statistics.(1), 93–106.
[汪大勋, 高旭亮, 蔡艳, 涂冬波. (2020). 基于类别水平的多级计分认知诊断Q矩阵修正:相对拟合统计量视角.(1), 93–106.]
Wang, D., Gao, X., Han, Y., & Tu, D. (2018). A simple and effective Q-matrix estimation method: From non-parametric perspective.(1), 180–188.
[汪大勋, 高旭亮, 韩雨婷, 涂冬波. (2018). 一种简单有效的Q矩阵估计方法开发:基于非参数化方法视角.(1), 180–188.]
Wang, W., Song, L., Ding, S., Meng, Y., Cao, C., & Jie, Y. (2018). An EM-based method for Q-matrix validation.(6), 446–459.
Yu, X. F., & Cheng, Y. (2020). Data-driven Q-matrix validation using a residual-based statistic in cognitive diagnostic assessment.(Suppl 1), 145–179
Yu, X., Luo, Z., Qin, C., Gao, C., & Li, J. (2015). Joint estimation of model parameters and Q-matrix based on response data.(2), 273–282.
[喻晓锋, 罗照盛, 秦春影, 高椿雷, 李喻骏. (2015). 基于作答数据的模型参数和Q矩阵联合估计.(2), 273–282.]
An empirical Q-matrix validation method using complete information matrix in cognitive diagnostic models
LIU Yanlou1, WU Qiongqiong2
(1Academy of Big Data for Education; Qufu Normal University, Jining 273165, China)(2School of Psychology, Qufu Normal University, Jining 273165, China)
A Q-matrix, which defines the relations between latent attributes and items, is a central building block of the cognitive diagnostic models (CDMs). In practice, a Q-matrix is usually specified subjectively by domain experts, which might contain some misspecifications. The misspecified Q-matrix could cause several serious problems, such as inaccurate model parameters and erroneous attribute profile classifications. Several Q-matrix validation methods have been developed in the literature, such as the G-DINA discrimination index (GDI), Wald test based on an incomplete information matrix (Wald-IC), and Hull methods. Although these methods have shown promising results on Q-matrix recovery rate (QRR) and true positive rate (TPR), a common drawback of these methods is that they obtain poor results on true negative rate (TNR). It is important to note that the worse performance of the Wald-IC method on TNR might be caused by the incorrect computation of the information matrix.
A new Q-matrix validation method is proposed in this paper that constructs a Wald test with a complete empirical cross-product information matrix (XPD). A simulation study was conducted to evaluate the performance of the Wald-XPD method and compare it with GDI, Wald-IC, and Hull methods. Five factors that may influence the performance of Q-matrix validation were manipulated. Attribute patterns were generated following either a uniform distribution or a higher-order distribution. The misspecification rate was set to two levels:= 0.15 and= 0.3. Two sample sizes were manipulated: 500 and 1000. The three levels of IQ were defined as high IQ,P(0) ~(0, 0.2) andP(1) ~(0.8, 1); medium IQ, P(0) ~(0.1, 0.3) andP(1) ~(0.7, 0.9); and low IQ, P(0) ~(0.2, 0.4) andP(1) ~(0.6, 0.8). The number of attributes was fixed at= 4. Two ratios of the number of items to attribute were considered in the study:= 16[(= 4)×(= 4)] and= 32[(= 4)×(= 8)].
The simulation results showed the following.
(1) The Wald-XPD method always provided the best results or was close to the best-performing method across the different factor levels, especially in the terms of the TNR. The HullP and Wald-IC methods produced larger values of QRR and TPR but smaller values of TNR. A similar pattern was observed between HullP and HullR, with HullP being better than HullR. Among the Q-matrix validation methods considered in this study, the GDI method was the worst performer.
(2) The results from the comparison of the HullP, Wald-IC, and Wald-XPD methods suggested that the Wald-XPD method is more preferred for Q-matrix validation. Even though the HullP and Wald-IC methods could provide higher TPR values when the conditions were particularly unfavorable (e.g., low item quality, short test length, and low sample size), they obtain very low TNR values. The practical application of the Wald-XPD method was illustrated using real data.
In conclusion, the Wald-XPD method has excellent power to detect and correct misspecified q-entry. In addition, it is a generic method that can serve as an important complement to domain experts’ judgement, which could reduce their workload.
cognitive diagnostic models, Q-matrix, XPD information matrix, Wald test
2022-03-09
* 国家自然科学基金青年项目(31900794)、山东省自然科学基金项目(ZR2019BC084)资助。
吴琼琼为共同第一作者。
B841
刘彦楼, E-mail: liuyanlou@163.com
