三维虚拟空间中转头选中远离和靠近运动目标的操作特性差异*

邓成龙 耿 鹏 蒯曙光,2

三维虚拟空间中转头选中远离和靠近运动目标的操作特性差异*

邓成龙1耿 鹏1蒯曙光1,2

(1华东师范大学心理与认知科学学院, 脑科学与教育创新研究院, 上海市心理健康与危机干预重点实验室, 上海 200026) (2上海脑科学与类脑研究中心, 上海 200031)

通过转头选中运动目标是虚拟现实(VR)中的常见操作, 然而运动目标包含远离和靠近运动, 确定两类操作的时间特性差异对设计高效的用户接口有重要的意义。本研究选取17名被试在VR中通过转头将球体光标快速准确地放入水平运动的球体目标内, 并改变初始距离、目标容差和目标速度。总时间结果显示, 远离运动的操作难度更大, 初始距离和目标容差对远离和靠近运动的影响相似, 目标速度对两类运动的影响相反。进一步将光标的移动过程划分为加速、减速和调整阶段, 结果发现, 远离运动的加速和减速时间大于靠近运动, 但是两类运动的调整时间接近, 并且只有目标容差对两类运动的影响一致。最后构建了总时间与三因素的函数模型, 成功解释了两类运动的操作时间特性。本研究证明了远离与靠近运动具有不同的操作时间特性, 为两类运动的独立交互设计提供了重要参考。

运动目标, 转头操作, 移动轨迹, 人体绩效建模, 人机交互

1 引言

近年来, 转头交互已经成为了VR中的重要交互方式, 一方面, 转头交互是很多不提供交互手柄的便携式VR和AR设备的主要交互方式, 比如Samsung GearVR, Google Cardboard和Microsoft HoloLens等(Blattgerste et al., 2018; Pathmanathan et al., 2020); 另一方面, 在很多VR应用中, 转头交互也作为双手被占用时的主要交互方式, 比如在虚拟手术训练中通过转头与显示屏交互(Hatscher et al., 2017)。在基于转头交互的大量应用中, 经常涉及选中移动目标任务, 比如行人、汽车等, 为了设计高效的用户接口, 了解影响转头选中运动目标的重要因素以及建立操作时间与影响因素的函数关系非常重要。以往研究详细探讨了VR中转头选中静止目标的操作时间特性(Hansen et al., 2018; Hoffmann et al., 2017; Jagacinski & Monk, 1985; Qian & Teather, 2017), 这些研究发现完成时间()与初始距离()和目标宽度()符合费茨定律：

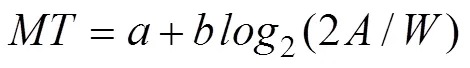
其中和是拟合常数。然而, 该模型并不能解释选中运动目标的操作特性, 因为选中运动目标的操作时间还受到目标速度大小的影响。此外, 运动目标还具有方向性, 目标做远离和靠近操作者的运动是两类常见的运动模式, 选中远离运动目标(简称远离运动)和靠近运动目标(简称靠近运动)的过程存在不同。在远离运动中, 操作者需要以大于目标的速度追击目标; 在靠近运动中, 操作者则需要对目标进行拦截, 如果拦截失败, 后续操作将变成追击远离运动目标模式(Port et al., 1997; Tresilian, 2005; Tresilian & Lonergan, 2002), 因此远离与靠近运动可能存在不同的操作时间特性。

目前没有发现在三维空间中探讨转头选中运动目标的研究, 但是少量研究者探讨了在二维屏幕上基于手控选中运动目标的操作时间特性, 然而远离与靠近运动的操作时间特性差异还不确定。远离运动的操作时间特性相对简单, 减小目标大小或者增大目标速度都增加操作时间(Hajri et al., 2011; Hasan et al., 2011; Ilich, 2009)。然而靠近运动的操作时间特性相对复杂。一方面, 一些研究发现靠近运动与远离运动具有相似的操作时间特性, 减小目标宽度或者增大目标速度会增加选中靠近运动目标的难度(Hajri et al., 2011; Jagacinski et al., 1980), 并且还提出了函数模型量化靠近运动的操作时间特性。比如, Jagacinski等人(1980)让参与者在二维电脑屏幕上使用摇杆控制一条竖直的直线(光标)放入逐渐靠近的由两条竖直直线组成的目标内。他们发现完成时间受到初始距离()、目标宽度()和目标速度()的影响, 并建立如下模型描述操作时间与三个因素的函数关系(Jagacinski et al., 1980)：

其中、和是拟合常数。后来Hoffmann在费茨定律基础上, 提出了靠近运动的两阶段模型：

近期, 不少研究从其他方面对选中运动目标的操作特性进行了探索, 比如Huang等人研究了不同因素对远离运动和靠近运动落点分布的影响(Huang et al., 2018; Huang et al., 2019), 不同因素对预估目标到达指定区域的影响(Lee et al., 2018)等, 但是这些研究没有探讨两类运动的操作时间变化, 由于操作时间是用户接口中最常用的指标, 因此本研究主要关注操作时间特性。虽然一些研究关注了操作时间, 比如视觉反馈和延时对操作时间的影响(Claypool et al., 2019; Mould & Gutwin, 2004), 提高选中运动目标操作效率的方法(Gunn et al., 2009; Hasan et al., 2011; Ortega, 2013; Ragan et al., 2020)等, 但是在这些研究中, 目标的运动方向不固定, 没有分离远离和靠近运动。

至今为止, 远离运动与靠近运动的操作时间特性差异还不完全清楚。首先, 初始距离和目标大小都是影响选中目标的重要因素, 减小目标和增大初始距离都会增加远离和靠近运动的难度, 但是两个因素对远离和靠近运动的影响是否存在差异还未可知。其次, 虽然已经确定增大目标速度会增加选中远离运动目标的难度, 但是目标速度如何影响选中靠近运动目标的表现还没有统一结论。选中静止目标的过程包含两个阶段：弹射阶段和调整阶段。在弹射阶段, 光标从起点快速移动到目标附近, 主要与初始距离相关; 调整阶段则根据视觉反馈实时调整光标的位置并对准目标, 同时受到目标大小和初始距离的影响(Deng et al., 2019; Elliott et al., 2001; Liu et al., 2009; Meyer et al., 1988)。一些研究也支持选中运动目标过程包含两个阶段(Hoffmann, 1991; Ilich, 2009), 并且目标速度影响两个阶段。增大目标速度将增加远离运动的实际移动距离和减少靠近运动的实际移动距离, 同时也会增加对准目标的难度。基于远离与靠近运动的操作过程差异, 我们提出如下推测。推测1: 在弹射阶段, 靠近运动的操作时间低于远离运动, 因为靠近运动的实际移动距离更短; 在调整阶段, 靠近运动的调整时间也低于远离运动, 因为远离运动的目标更远, 调整难度更大。基于两阶段的结果, 靠近运动的总时间将更低。推测2：随着目标速度的增加, 靠近运动总时间呈现先下降后上升的U型变化趋势。增大目标速度减少弹射阶段的时间, 但是也增加调整阶段的时间。以往研究显示转头交互具有移动速度慢、稳定性高的特点(Bates & Istance, 2003; Deng et al., 2019), 因此我们推测, 目标速度的小幅度增加对弹射阶段的帮助更大, 导致总操作时间下降。但是目标速度进一步增加将导致调整时间快速增加, 超过弹射阶段的受益时间, 导致总时间开始上升。推测3：靠近运动的U型曲线拐点速度还受到目标大小的影响, 目标越小, 调整难度越高, 拐点速度越小。

本研究的目的是探索VR中转头选中远离运动目标与靠近运动目标的操作时间特性差异。本研究采用VR中常见的放置任务, 将一个球形光标放入指定的球形目标内(Deng et al., 2019; Duval & Fleury, 2009; Teather & Stuerzlinger, 2007)。由于放置任务研究显示操作时间受到目标容差(光标与目标的大小差值)而不是目标大小的规律性影响(Deng et al., 2019; MacKenzie & Teather, 2012; Pastel, 2011), 因此我们设置不同的目标容差大小。此外, 我们还改变了初始距离(光标与目标中心的直线距离)和目标移动速度。Deng等人(2019)在VR中使用转头交互完成静止目标的放置任务, 他们将光标的移动过程划分成加速阶段、减速阶段和调整阶段, 其中加速阶段和减速阶段之和代表了弹射阶段(Deng et al., 2019)。在本研究中, 我们参照Deng等人的方法将光标的移动过程划分成三个阶段, 系统地分析三个因素对远离运动与靠近运动的影响差异。最后, 我们提出函数模型描述了远离运动和靠近运动的总操作时间与三个因素的关系, 我们的研究结果将对VR中的交互设计提供重要帮助。

2 方法

2.1 被试

本研究采用G*Power 3.1软件预估样本大小, α水平和统计检验力分别设置为0.05和0.95, 根据相关文献中的效应量, 取η2p> 0.2 (Deng et al., 2019), 计算出最少需要12名被试, 同时参考同类研究主要采用15～20名被试, 因此本实验一共招募了17名大学生(7名男性, 年龄：22.5 ± 2.5岁, 身高：165.8 ± 6.4 cm)。所有被试均为右利手, 身体健康, 视力或矫正视力正常, 无颈部转动障碍。所有被试在实验前签署了由学校学术伦理委员会批准的知情同意书, 且在实验后获得适当报酬。

2.2 实验仪器和材料

本研究使用Oculus Rift CV1沉浸式虚拟现实头盔(单眼分辨率：1080×1200; 刷新率：90 Hz; 最大视角：110°), 头盔包含基于惯性测量单元(IMU)的转动传感器和基于红外光学的位置传感器, 能够实时获得头的6自由度空间位置(x, y, z, yaw, pitch, row) (图1a)。在实验中关闭了头盔的红外光学位置追踪功能, 被试只能通过转头完成任务。

实验程序采用Unity3D和C#编写, 在Dell Alienware Area(操作系统：windows 8.1; CPU：Intel core i7; 显卡：NVIDA GeForce GTX TITAN)电脑上运行, 确保程序按照头盔的最大刷新率运行。

2.3 实验刺激和设计

实验场景和实验刺激如图1所示, 在一个虚拟的空间中竖直放置了一块2000 m × 2000 m的灰色平面作为背景, 在平面前方呈现了一个黄色小球作为光标和一个白色半透明小球作为目标。光标和目标分别随机出现在被试正前方3 m的左(右)侧和右(左)侧区域, 高度为被试的眼高。目标在水平方向上做远离光标或者靠近光标的匀速直线运动。

为了确定参数范围, 我们进行了一项预实验。结果显示, 光标大小和转头方向对操作时间和正确率没有显著影响, 因此不作为本实验的研究因素。考虑到目标的最大值以及远离运动中光标的可见程度, 我们固定光标的直径为4°。为了能够有效完成任务(错误率低于30%), 目标的最大速度设置为2 m/s, 目标容差不低于4°, 初始距离的最大值为40°。目标的最小速度设置为0.5 m/s, 以便能够快速识别出目标是运动的。在靠近运动中, 为了确保在最大速度情况下能够大概率成功拦截目标, 初始距离的最小值设置为20°。此外, 目标容差的最大值设置为8°, 因为选中目标的难度已经较低。考虑到总的试次数量、疲劳程度以及目标速度的重要性, 我们设置了4个水平的目标移动速度、3个水平的目标容差和2个水平的初始距离, 根据参数的最大值和最小值等分。

综上所述, 本实验采用2 (目标运动方向：远离运动, 靠近运动) × 4 (目标移动速度：0.5 m/s, 1 m/s, 1.5 m/s, 2 m/s) × 2 (初始距离：20°, 40°) × 3 (目标容差：4°, 6°, 8°)的四因素被试内重复实验设计。光标直径约0.22 m (4°), 目标容差的线性量大小分别约0.22 m、0.33 m和0.43 m, 目标大小为目标容差与光标大小之和, 直径为8°(0.43 m)、10°(0.54 m)和12°(0.65 m), 初始距离的线性距离为1.06 m和2.18 m。本研究采用角度表示参数大小是因为三维空间中角度量包含了深度对操作时间的影响(Kopper et al., 2010; Qian & Teather, 2017; 邓成龙, 蒯曙光, 2021)。

图1 实验设计示意图

注：(a)实验装置和被试操作示意图, 被试佩戴VR头盔坐在电脑前完成任务; (b)实验刺激场景, 黄色小球为光标, 白色半透明大球为目标; (c)选中远离运动目标任务的相关参数和操作过程示意图, 实验参数包括初始距离(光标与目标中心的直线距离对应的视角大小), 目标容差(光标与目标的视角大小差值)和目标速度, 光标大小固定为4°, 目标在水平方向上移动并远离光标; (d)选中靠近运动目标的操作过程示意图, 目标在水平方向上移动并靠近光标。

实验一共包含23个组块(block), 每个组块包含所有的48种实验条件组合, 组块内不同条件组合顺序随机呈现。为了避免长时间使用VR头盔导致的视觉疲劳、脖子疲劳以及眩晕, 相关研究建议VR的连续使用时间小于1小时(Smith & Burd, 2019), 因此本实验分两天进行。第一天为练习, 完成8个组块, 第二天为正式实验, 完成剩下的15个组块。练习和正式测试的总时间分别约1小时。组块与组块之间休息1分钟, 由于不同人对虚拟现实引起的眩晕敏感性不同, 为了确保数据不受眩晕的影响, 在测试的过程中, 被试如果感觉不适, 随时可以在试次间隙休息。

2.4 实验过程

实验设置如图1a所示, 被试坐在固定的椅子上, 佩戴虚拟现实头盔, 手握手柄。在虚拟场景中被试将看到两个球体, 视野左侧(右侧)的黄色小球为光标, 视野右侧(左侧)的白色半透明的大球为目标(图1b)。被试视野正前方的绿色小点代表被试头的朝向, 当被试转头看向场景中的光标时, 按下手柄上的按键, 光标颜色从黄色变成红色, 并且光标的移动由被试转头控制, 同时目标开始按照设定的速度在水平方向上做远离或者靠近光标的匀速运动。此时被试通过转头尽可能又快又准地将光标完全放入目标内, 并按下手柄上的按键确认完成任务。如果光标没有完全放入目标球内, 则表示任务失败, 程序播放错误提示音。实验程序记录每次任务的完成时间、光标的移动轨迹和所有任务的错误率, 轨迹采样率为90 Hz。

2.5 数据分析

根据测试经验, 在正常操作情况下, 完成任务的总时间在300 ms至2500 ms之间。完成时间大于2500 ms可能是由于程序卡顿导致, 而完成时间小于300 ms可能是被试误操作比如双击按键导致, 因此我们将总完成时间大于2500 ms和小于300 ms的试次剔除, 共计删除25个试次, 占总试次的0.20%。

我们对光标移动速度轨迹进行处理。首先, 我们对轨迹数据进行10 Hz的低通滤波, 减少噪声对数据的影响(Chen et al., 2015; Liu et al., 2009)。其次, 我们将光标速度轨迹划分成3个阶段：加速阶段、减速阶段和调整阶段, 3个阶段的划分方法在基于选中静止目标过程的划分方法基础上进行修改, 以满足选中运动目标过程(Deng et al., 2019)。加速阶段与减速阶段的分界点为光标移动的最大速度对应位置, 减速阶段与调整阶段的分界点为第一个满足下面三个标准中的任意一个的点, 且速度小于目标速度与光标最大速度的中点值(远离运动)或者速度小于光标最大速度的一半(靠近运动) (图2)：

图2 一位被试选中远离运动目标(a)和靠近运动目标(b)过程的光标速度轨迹和三个阶段的划分样例

(1) 远离运动：光标速度从大于目标移动速度变为小于目标移动速度的第一个点; 靠近运动：光标移动速度的正负方向改变的第一个点。

(2) 光标的加速度值从负数变为正数的第一个点, 即光标速度从减速变为加速的点。

(3) 光标的加速度一直为负值, 但其绝对值小于加速度最大值0.1倍的点。

减速阶段与调整阶段的分界点需要考虑速度的正负值, 由于目标的运动方向为水平方向, 因此使用光标在水平方向的速度方向代表总体速度的方向(Deng et al., 2019)。

我们对15个组块的总平均完成时间进行方差分析, 查看操作过程是否存在练习或者疲劳效应。结果显示, 虽然组块顺序的主效应显著((3.10, 49.59) = 6.12,= 0.001, η2p= 0.28, Greenhouse- Geisser矫正), 但是组块完成时间并没有随着组块顺序的增加而持续性地下降或者上升。对组块顺序进行Bonferroni事后检验, 发现只有组块1的完成时间(984 ± 161 ms)显著高于组块12 (857 ± 121 ms,= 0.005)和组块13 (842 ± 101 ms,= 0.030), 其他组块之间的时间差异不显著。该结果说明操作过程不存在练习效应和疲劳效应, 因此我们采用15个组块的数据平均值用于后续分析。

本研究采用SPSS Statistics 21.0对数据进行多因素重复测量方差分析, 并采用Greenhouse-Geisser方法对不满足球形假设检验的结果进行校正。时间分析只采用正确试次的数据。

3 实验结果

3.1 错误率

完成任务的错误率如图3所示, 远离和靠近运动的最大错误率低于30%, 平均错误率分别只有7.38 ± 3.31%和5.85% ± 3.24%, 说明被试能够很好地完成任务。对错误率进行四因素(目标运动方向, 目标移动速度, 初始距离和目标容差)重复测量方差分析, 结果显示目标速度((1.62, 25.88) = 40.13,< 0.001, η2p= 0.72)和目标容差((1.19, 19.05) = 71.23,< 0.001, η2p= 0.82)的主效应显著, 两类运动的错误率都随着目标速度的增大而增加, 随着目标容差的增大而降低。初始距离对远离和靠近运动造成了相反的影响, 初始距离与目标运动方向存在显著的交互效应((1, 16) = 21.92,< 0.001, η2p= 0.58), 简单效应分析显示, 在远离运动中, 初始距离40°的错误率高于初始距离20°的错误率(= 0.013), 但是在靠近运动中, 初始距离20°的错误率则高于初始距离40°的错误率(< 0.001)。目标运动方向的主效应显著((1, 16) = 8.01,= 0.012, η2p= 0.33), 远离运动的平均错误率显著高于靠近运动的错误率, 但是随着目标容差的增大, 两者的差异逐渐减小, 目标运动方向与目标容差的交互效应显著((1.31, 21.01) = 7.19,= 0.009, η2p= 0.31)。此外, 目标运动方向、初始距离和目标速度还存在显著的三因素交互效应((1.57, 25.15) = 11.94,= 0.001, η2p= 0.43), 当初始距离为20°时, 随着目标速度的增大, 远离与靠近运动的错误率也逐渐接近, 特别是当目标速度达到2 m/s, 靠近运动的错误率已经高于远离运动; 相反, 当初始距离增大到40°, 两者的错误率差异则随着目标速度的增大而增加。其它的交互效应不显著。

图3 完成任务的错误率

注：选中远离运动目标和靠近运动目标的错误率与初始距离(a)、目标容差(b)和目标移动速度(c)的关系图。图中误差线为标准误, 余同。

3.2 完成任务的总时间

对正确试次的总完成时间进行重复测量方差分析, 探索三个因素对远离和靠近运动的影响差异。结果如图4所示, 目标运动方向的主效应显著((1, 16) = 99.64,< 0.001, η2p= 0.86), 远离运动的平均总完成时间(986 ± 120 ms)显著高于靠近运动的完成时间(784 ± 124 ms), 说明选中远离运动目标的难度更大。初始距离((1, 16) = 221.85,< 0.001, η2p= 0.93)和目标容差((1.04, 16.61) = 69.94,< 0.001, η2p= 0.81)的主效应显著, 两个因素对远离和靠近运动造成了相似的影响, 两类运动的完成时间都随着初始距离的增大而增加, 随着目标容差的增大而减少。然而目标运动方向与初始距离存在显著的交互效应((1, 16) = 8.59,= 0.01, η2p= 0.35), 靠近运动的时间增长速度稍快于远离运动, 说明初始距离对靠近运动的影响更大。目标运动方向与目标容差的交互效应不显著((1.13, 18.07) = 1.60,= 0.225), 表明目标容差对远离和靠近运动的影响一致。与前两个因素不同, 目标速度对远离运动和靠近运动造成了相反的影响, 目标速度与目标运动方向存在显著的交互效应((1.44, 22.96) = 60.74,< 0.001, η2p= 0.79)。对远离和靠近运动单独进行方差分析发现, 随着目标速度的增大, 远离运动的操作时间快速增加((1.38, 22.11) = 48.49,< 0.001, η2p= 0.75), 相反, 靠近运动的操作时间快速下降((1.16, 18.59) = 12.43,= 0.002, η2p= 0.44)。然而, 随着目标速度的减小, 运动目标逐渐变成静止目标, 因此远离与靠近运动的操作难度逐渐接近, 当目标速度降低到0.5 m/s时, 两类运动的完成时间已经没有显著差异(= 0.996 )。此外, 目标运动方向、目标速度和初始距离还存在显著的三因素交互效应((1.86, 29.82) = 4.03,= 0.031, η2p= 0.20), 独立分析两类运动发现, 靠近运动中初始距离与目标速度的交互效应显著((1.79, 28.57) = 3.72,= 0.041, η2p= 0.19), 当初始距离为20°时, 靠近运动的操作时间表现出了微弱的U型曲线, 目标速度从0.5 m/s增加到1.5 m/s再增加到2 m/s, 操作时间先快速下降后缓慢上升, 证明了我们的推测2 (图4c)。然而, 我们没有发现U型曲线的拐点速度受到目标容差的影响, 目标容差与目标速度不存在显著的交互效应((3.07, 49.13) = 0.70,= 0.563), 否定了我们的推测3。除此之外, 不存在其他显著的交互效应。

3.3 光标移动过程的三阶段操作时间

进一步比较远离与靠近运动在三个阶段的差异, 结果如图5所示。在加速阶段, 目标运动方向的主效应显著((1, 16) =162.32,< 0.001, η2p= 0.91), 远离运动的加速时间(386 ± 58 ms)大于靠近运动的加速时间(255 ± 33 ms), 说明远离运动需要更长的时间到达速度峰值。初始距离对远离和靠近运动造成了相反的影响, 目标运动方向与初始距离的交互效应显著((1, 16) = 179.00,< 0.001, η2p= 0.92), 对两类运动单独进行方差分析显示, 初始距离的增大减少了远离运动的加速时间((1, 16) = 50.26,< 0.001, η2p= 0.76), 但是增加了靠近运动的加速时间,(1, 16) = 90.03,< 0.001, η2p= 0.85。目标速度仍然对两类运动的影响相反, 与总时间的结果一致, 目标运动方向与目标速度的交互效应显著,(1.46, 23.42) = 55.82,< 0.001, η2p= 0.78。此外, 目标运动方向、目标移动速度和初始距离还存在显著的三因素交互效应((2.08, 33.29) = 28.26,< 0.001, η2p= 0.64), 在远离和靠近运动中, 初始距离20°与40°的时间差异变化略有不同。目标容差的主效应不显著((2, 32) = 0.04,= 0.962), 以及目标容差与目标运动方向的交互效应不显著((1.30, 20.86) = 0.80,= 0.41), 加速时间不受目标容差的影响。目标运动方向、初始距离和目标容差的三因素交互效应显著((2, 32) = 3.94,= 0.029, η2p= 0.20), 在不同目标容差下, 初始距离对远离和靠近运动的影响稍有不同。除此之外, 没有其他显著的交互效应(图5a)。

图4 完成任务的总时间

注：选中远离运动目标和靠近运动目标的总操作时间与初始距离(a)、目标容差(b)和目标速度(c)的关系图。

图5 光标移动过程的三阶段操作时间结果

注：加速阶段时间(a)、减速阶段时间(b)和调整阶段时间(c)与初始距离(上)、目标容差(中)和目标速度(下)的关系图。

在减速阶段, 远离运动的减速时间(342 ± 29 ms)仍然大于靠近运动的减速时间(272 ± 33 ms), 目标运动方向的主效应显著,(1, 16) =119.31,< 0.001, η2p= 0.88。目标速度((1.75, 28.07) = 97.85,< 0.001, η2p= 0.86)和初始距离((1, 16) = 335.25,< 0.001, η2p= 0.95)的主效应显著, 并且目标运动方向与目标速度((1.95, 31.11) = 67.77,< 0.001, η2p= 0.81)以及目标运动方向与初始距离((1, 16) = 38.03,< 0.001, η2p= 0.70)的交互效应显著, 表明初始距离与目标速度对远离和靠近运动造成了不同的影响。与加速阶段不同, 初始距离对远离运动((1, 16) = 128.83,< 0.001, η2p= 0.89)和靠近运动((1, 16) = 309.80,< 0.001, η2p= 0.95)的影响相似, 都增加了减速时间, 但是靠近运动的时间增长速度更快。增加目标速度快速降低了靠近运动的调整时间((1.76, 28.20) = 195.38,< 0.001, η2p= 0.92), 但是对远离运动只有轻微影响((1.73, 27.66) = 11.28,< 0.001, η2p= 0.41)。此外, 目标运动方向、初始距离和目标速度还存在显著的三因素交互效应((3, 48) = 4.37,= 0.008, η2p= 0.21), 在远离和靠近运动中, 初始距离40°与20°的时间差异变化稍有不同。虽然目标容差的主效应显著((2, 32) = 7.65,= 0.002, η2p= 0.32), 以及目标容差与目标运动方向的交互效应显著((2, 32) = 6.36,= 0.005, η2p= 0.28), 但是远离运动和靠近运动的减速时间最大平均值差异非常小, 分别只有18 ms和2 ms, 说明目标容差对减速时间的影响很小。除此之外, 其他的交互效应都不显著(图5b)。

在调整阶段, 与前两个阶段不同, 目标运动方向的主效应不显著((1, 16) = 0.001,= 0.974), 远离运动(258 ± 107 ms)与靠近运动(259 ± 132 ms)的平均调整时间非常接近, 但是两类运动仍然在初始距离和目标移动速度水平上表现出了差异, 目标运动方向与初始距离的交互效应((1, 16) = 31.22,< 0.001, η2p= 0.66)以及目标运动方向与目标速度的交互效应((1.69, 26.97) = 8.34,= 0.002, η2p= 0.34)都显著。对两类运动单独分析显示, 远离运动的调整时间同时与初始距离((1, 16) = 129.81,< 0.001, η2p= 0.89)和目标移动速度((1.30, 20.73) = 25.32,< 0.001, η2p= 0.61)有关, 但是靠近运动的调整时间则不受初始距离((1, 16) = 0.14,= 0.711)的影响。虽然靠近运动的调整时间随着目标移动速度的增大而缓慢增加, 但是统计结果没有达到显著水平,(1.35, 21.66) = 0.63,= 0.48。此外, 目标容差的主效应显著((1.08, 17.25) = 55.46,< 0.001, η2p= 0.78), 远离与靠近运动的调整时间都随着目标容差的增大而快速下降, 并且目标容差与目标运动方向的交互效应不显著((1.32, 21.18) = 0.20,= 0.728), 说明目标容差对两者的调整难度影响一致。除此之外, 剩余的交互效应都不显著(图5c)。

3.4 模型拟合

远离和靠近运动的操作时间()受到初始距离()、目标容差()和目标速度()的影响, 我们建立操作时间与三个影响因素的函数关系, 量化两类运动的操作时间特性。我们取正确试次的数据, 然后将所有被试相同条件的数据平均。为了与目标速度单位(m/s)保持一致, 我们将初始距离和目标容差的角度量转换成了线性量。前人已经提出了量化靠近运动操作时间特性的公式2和公式3, 我们将目标容差代替目标宽度, 将数据代入上述两个公式。结果显示两个公式并不能很好地解释本研究的靠近运动(公式2：2= 0.449; 公式3：2= 0.628)和远离运动(公式2：2= 0.900; 公式3：2= 0.610)的数据, 因此需要建立新的函数模型。由于初始距离和目标容差对选中运动目标的操作时间影响与选中静止目标的影响非常相似, 因此我们在费茨定律(公式1)的基础上进行修改, 加入目标速度参数。由于远离运动的完成时间随着目标速度的增大而线性增加, 而靠近运动的完成时间随着目标速度的增大而下降, 并且目标速度与初始距离和目标容差不存在强交互效应, 因此在新模型中目标速度作为独立参数, 我们提出新的模型如下：

其中、和是拟合常数,是任务难度,是指数, 当= 1时, 公式4代表远离运动模型; 当= −1时, 公式4代表靠近运动模型。

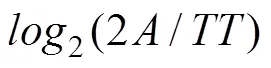
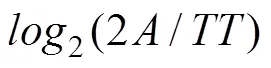
为了验证模型的稳定性, 我们把被试的数据随机分成训练集和测试集。训练集由随机挑选出的2/3被试(11人)的数据组成, 然后使用公式4对训练集进行拟合, 用获得的模型参数预测剩下的1/3被试(6人)的数据。我们重复这个过程1000次, 获得了训练集数据的模型拟合2结果以及对测试集数据的模型预测2结果的分布(图6c)。靠近运动和远离运动的测试集平均2分别为0.940和0.966, 与所有数据的拟合结果(靠近运动：2= 0.952, 远离运动：2= 0.971)非常接近。在远离运动中, 模型预测的2全部超过了0.8, 平均值达到了0.941。虽然靠近运动的模型预测结果低于远离运动模型的预测结果, 但是75%的靠近运动模型的预测2超过了0.82, 平均值仍然达到了0.855。本结果说明我们提出的模型不仅稳定, 还能够很好地对数据进行预测。

4 讨论

在VR中通过转头交互选中远离运动目标和靠近运动目标是常见的操作, 然而远离运动与靠近运动的操作时间特性差异还不清楚。本研究在分析总操作时间的基础上, 进一步地将光标的移动过程划分成加速阶段、减速阶段和调整阶段, 结合三个阶段的操作时间系统探索了初始距离、目标容差和目标移动速度对两类运动的影响差异。我们的结果证明了远离运动与靠近运动即有相同的操作时间特性, 也存在不同的操作时间特性。一方面, 目标容差对两类运动的影响一致, 而且只影响调整阶段, 不影响加速和减速时间, 说明被试在将光标快速移动到目标附近的过程中并不考虑目标的大小, 该结果与选中静止目标的分段结果一致(Chen et al., 2015; Deng et al., 2019)。另一方面, 初始距离对远离和靠近运动造成了不同的影响。虽然在总时间上, 远离与靠近运动在不同初始距离水平上表现非常相似, 但是在三阶段操作时间上, 初始距离对两类运动的影响存在显著差异。初始距离影响远离运动的三个阶段, 但是只影响了靠近运动的加速和减速阶段。靠近运动的调整时间不受初始距离远近的影响, 原因可能是在调整阶段目标出现在操作者附近, 导致光标对准目标的难度基本一致。

图6 公式4对远离和靠近运动数据的拟合结果

此外, 目标速度对远离运动和靠近运动的影响也不同。在远离运动中, 目标速度的增大增加了加速阶段和调整阶段的时间, 导致总操作时间增加, 支持了以前的研究结果(Hajri et al., 2011; Hasan et al., 2011; Ilich, 2009)。在靠近运动中, 目标速度的增大减少了加速阶段与减速阶段的时间, 增加了调整阶段的时间。由于前两个阶段减少的时间大于调整阶段增加的时间, 导致靠近运动的总时间下降。然而, 我们的结果与以前的研究结果存在差异, 前人发现在大部分情况下操作时间随着目标速度的增大而快速增加(Hajri et al., 2011; Ilich, 2009; Jagacinski et al., 1980), 产生不同结果的原因可能存在两个方面。一方面, 操作任务不同可能导致结果不同。比如, 在Ilich (2009)和Hajri等人(2011)的研究中, 远离与靠近运动没有完全分离, 而本研究的远离与靠近运动完全独立。另一方面, 不同的操作方式具有不同的操作特性, 也可能导致结果存在差异。以往研究主要采用鼠标或者摇杆等交互方式完成任务, 但是转头交互与摇杆和鼠标操作的完成时间存在显著差异(Jagacinski & Monk, 1985; Jalaliniya et al., 2014; Lin et al., 1992), 转头交互的稳定性可能比摇杆和鼠标更好, 因此调整时间受目标速度的影响更小。另外, 我们发现当初始距离为20°时, 靠近运动的操作时间与目标速度存在U型关系。当目标速度在一定范围内时, 加速和减速阶段减少的时间多于增加的调整时间, 当目标速度超过一个阈值后, 这种优势将不存在。从图5可以看出, 当目标速度从1.5 m/s增加到2 m/s时, 加速时间和减速时间分别只减少了4 ms和14 ms, 但是调整时间增加了66 ms。该结果证明了我们的推测2, 也支持了先前的研究结果(Ilich, 2009)。然而我们没有发现U型曲线的拐点速度受到目标容差的影响, 否定了推测3, 原因可能与目标容差不够小有关, 导致调整阶段的难度不高。

本研究还揭示了远离运动与靠近运动的操作难度差异。从总时间来看, 选中远离运动目标的总时间更长, 说明操作难度更高, 但是从三个阶段来看, 远离与靠近运动的时间差异主要体现在加速阶段和减速阶段, 而两者的调整时间接近。该结果部分支持了推测1, 在推测1中, 我们认为在三个阶段, 远离运动的操作时间都大于靠近运动。首先, 加速和减速阶段的操作时间由实际移动距离决定, 由于远离运动的实际移动距离更长, 因此在前两个阶段花费更长的时间, 并且目标速度越快, 两类运动的实际移动距离差异越大, 导致两个阶段的时间差异越大, 支持了推测1。其次, 在调整阶段, 远离目标的位置比靠近运动的目标位置更远, 对准难度更大, 但是两类运动的调整时间非常接近, 与推测1不符, 原因可能与头控交互的良好稳定性有关(Bates & Istance, 2003; Kytö et al., 2018), 导致调整时间不容易受影响。然而, 我们的结果显示, 当目标速度超过1.5m/s后, 远离运动的调整时间开始超过靠近运动的调整时间, 我们猜测当目标速度进一步增大时, 两者的调整时间差异可能到达显著水平。

本研究的结果具有多方面的应用价值。第一, 远离运动与靠近运动存在不同的操作时间特性, 提示三维空间的交互设计人员应该分开考虑两类运动的用户接口设计, 提高操作效率和用户体验。第二, 由于多个因素都对选中运动目标的任务难度产生了重要影响, 我们提出的函数模型量化了任务难度, 可以帮助交互设计人员有效地选择参数范围。第三, 研究结果还可以帮助了解现实生活中通过其他方式选中运动目标的操作过程, 比如运动员击打飞碟, 为相关运动的训练提供参考依据。最后, 我们的模型还可能应用于脖子转动相关疾病的初步检测, 比如比较健康人群与脖子疼痛人群的表现差异(Descarreaux et al., 2010; Marchand et al., 2014), 为相关疾病的预防提供参考建议。

本研究也存在一定的不足。首先, 在本研究中, 我们只考虑了目标在水平方向上的移动, 没有验证目标在垂直方向和纵深方向上移动的结果。目标在不同维度上移动时, 头的转动方向也不同, 研究显示头朝不同方向转动的操作表现存在差异(Jagacinski & Monk, 1985; Radwin et al., 1990), 可能导致不同的结果。其次, 虽然初始距离和目标大小的角度量参数包含了深度因素对操作表现的影响(Kopper et al., 2010; Prytz et al., 2012; 邓成龙, 蒯曙光, 2021), 但是本研究的目标速度为线性速度, 线性目标速度在不同深度下对远离与靠近运动的影响差异是否相同还未被验证, 因此本研究的结论目前也只适用于深度为3 m的情况, 未来我们将进一步探索不同深度的结果, 扩展本研究的结论。

5 结论

本研究采用总操作时间和操作过程的三阶段(加速阶段、减速阶段和调整阶段)操作时间系统地分析了初始距离、目标容差和目标移动速度对VR中转头选中远离运动目标与靠近运动目标的影响差异。研究结果证明了初始距离和目标速度对远离运动和靠近运动造成了不同的影响, 目标容差对两类运动的影响一致。此外, 远离运动的操作难度更大, 但是难度差异主要发生在加速阶段和减速阶段。基于两类运动的操作时间特性, 本研究提出了一个新的模型解释远离和靠近运动的操作时间, 我们的模型提供了一种可以量化和评估人类通过转头选中运动目标操作时间特性的方法。

致谢：感谢田宸宇和赵铭对本研究的数据采集和分析提供的帮助。

Bates, R., & Istance, H. O. (2003). Why are eye mice unpopular? A detailed comparison of head and eye controlled assistive technology pointing devices.,(3), 280–290. https://doi.org/10.1007/ s10209-003-0053-y

Blattgerste, J., Renner, P., & Pfeiffer, T. (2018). Advantages of eye-gaze over head-gaze-based selection in virtual and augmented reality under varying field of views., Article 1, 1–9. https://doi.org/10.1145/3206343.3206349

Chen, Y., Hoffmann, E. R., & Goonetilleke, R. S. (2015). Structure of hand/mouse movements.,(6), 790–798. https://doi.org/1109/ THMS.2015.2430872

Claypool, M., Cockburn, A., & Gutwin, C. (2019). Game input with delay: Moving target selection parameters., 25–35. https://doi.org/10.1145/3304109.3306232

Deng, C.-L., Geng, P., Hu, Y.-F., & Kuai, S.-G. (2019). Beyond Fitts’s law: A three-phase model predicts movement time to position an object in an immersive 3D virtual environment.,(6), 879–894. https://doi.org/10.1177/ 0018720819831517

Deng, C.-L., & Kuai, S.-G. (2021). Angular parameters include the effect of depth on movement time for positioning task in virtual reality.,(6), 52– 58. https://doi.org/10.13837/j.issn.1006-8309.2021.06.0009

[邓成龙, 蒯曙光. (2021). 虚拟现实空间中角度量参数包含深度对放置任务操作时间的影响.,(6), 52–58. https://doi.org/10.13837/j.issn.1006-8309.2021.06.0009]

Descarreaux, M., Passmore, S. R., & Cantin, V. (2010). Head movement kinematics during rapid aiming task performance in healthy and neck-pain participants: The importance of optimal task difficulty.,(5), 445–450. https://doi.org/10.1016/j.math.2010.02.009

Duval, T., & Fleury, C. (2009). An asymmetric 2D pointer/3D ray for 3D interaction within collaborative virtual environments., 33–41. https://doi.org/10.1145/1559764. 1559769

Elliott, D., Helsen, W. F., & Chua, R. (2001). A century later: Woodworth's (1899) two-component model of goal-directedaiming.,(3), 342–357. https://doi.org/ 10.1037/0033-2909.127.3.342

Gunn, T. J., Irani, P., & Anderson, J. (2009). An evaluation of techniques for selecting moving targets., 3329–3334. https://doi.org/10.1145/1520340.1520481

Hajri, A. A., Fels, S., Miller, G., & Ilich, M. (2011). Moving target selection in 2D graphical user interfaces. In P. Campos, N. Graham, J. Jorge, N. Nunes, P. Palanque, & M. Winckler (Eds.),(Vol. 6947, pp. 141–161). Springer, Berlin, Heidelberg. https://doi.org/10.1007/ 978-3-642-23771-3_12

Hansen, J. P., Rajanna, V., MacKenzie, I. S., & Bækgaard, P. (2018). A Fitts' law study of click and dwell interaction by gaze, head and mouse with a head-mounted display., Article 7, 1–5. https://doi.org/10.1145/3206343. 3206344

Hasan, K., Grossman, T., & Irani, P. (2011). Comet and target ghost: Techniques for selecting moving targets., 839–848. https://doi.org/10.1145/1978942.1979065

Hatscher, B., Luz, M., Nacke, L. E., Elkmann, N., Müller, V., & Hansen, C. (2017). GazeTap: Towards hands-free interaction in the operating room., 243–251. https://doi.org/10.1145/3136755.3136759

Hoffmann, E. R. (1991). Capture of moving targets: A modification of Fitts' law.,(2), 211−220. https://doi.org/10.1080/00140139108967307

Hoffmann, E. R., Chan, A. H. S., & Heung, P. T. (2017). Head rotation movement times.,(6), 986−994. https://doi.org/10.1177/0018720817701000

Huang, J., Tian, F., Fan, X., Zhang, X., & Zhai, S. (2018). Understanding the uncertainty in 1D unidirectional moving target selection., Article 237, 1–12. https://doi.org/10.1145/3173574.3173811

Huang, J., Tian, F., Li, N., & Fan, X. (2019). Modeling the uncertainty in 2D moving target selection., 1031–1043. https://doi.org/10.1145/ 3332165.3347880

Ilich, M. V. (2009).(Unpublished master's thesis). University of British Columbia. https://doi.org/10.14288/1.0064925

Jagacinski, R. J., & Monk, D. L. (1985). Fitts’ law in two dimensions with hand and head movements.,(1), 77–95. https://doi.org/10.1080/ 00222895.1985.10735338

Jagacinski, R. J., Repperger, D. W., Ward, S. L., & Moran, M. S.(1980). A test of Fitts' law with moving targets.,(2), 225–233. https://doi.org/10.1177/00187208800 2200211

Jalaliniya, S., Mardanbeigi, D., Pederson, T., & Hansen, D. W. (2014). Head and eye movement as pointing modalities for eyewear computers., 50–53. https://doi.org/10.1109/BSN.Workshops. 2014.14

Kopper, R., Bowman, D. A., Silva, M. G., & McMahan, R. P. (2010). A human motor behavior model for distal pointing tasks.,(10), 603–615. https://doi.org/10.1016/j.ijhcs.2010.05.001

Kytö, M., Ens, B., Piumsomboon, T., Lee, G. A., & Billinghurst, M. (2018). Pinpointing: Precise head-and eye-based target selection for augmented reality., Article 81, 1–14. https://doi. org/10.1145/3173574.3173655

Lee, B., Kim, S., Oulasvirta, A., Lee, J.-I., & Park, E. (2018). Moving target selection: A cue integration model., Article 230, 1–12. https://doi.org/10.1145/3173574. 3173804

Lin, M. L., Radwin, R. G., & Vanderheiden, G. C. (1992). Gain effects on performance using a head-controlled computer input device.,(2), 159–175. https://doi.org/ 10.1080/ 00140139208967804

Liu, L., van Liere, R., Nieuwenhuizen, C., & Martens, J.-B. (2009). Comparing aimed movements in the real world and in virtual reality., 219–222. https://doi.org/10.1109/VR.2009.4811026

MacKenzie, I. S. (1992). Fitts' law as a research and design toolin human-computer interaction.,(1), 91–139. https://doi.org/10.1207/s15327051hci0701_3

MacKenzie, I. S., & Teather, R. J. (2012). FittsTilt: The application of Fitts' law to tilt-based interaction., 568–577. https://doi.org/ 10.1145/2399016.2399103

Marchand, A.-A., Cantin, V., Murphy, B., Stern, P., & Descarreaux, M. (2014). Is performance in goal oriented head movements altered in patients with tension type headache?,(1), 179. https://doi.org/10. 1186/1471-2474-15-179

Meyer, D. E., Abrams, R. A., Kornblum, S., Wright, C. E., & Keith Smith, J. (1988). Optimality in human motor performance: Ideal control of rapid aimed movements.,(3), 340–370. https://doi.org/10. 1037/0033-295x.95.3.340

Mould, D., & Gutwin, C. (2004). The effects of feedback on targeting with multiple moving targets., 25–32. https://dl.acm.org/doi/ 10.5555/1006058.1006062

Ortega, M. (2013). Hook: Heuristics for selecting 3D moving objects in dense target environments., 119–122. https://doi.org/10.1109/3DUI.2013.6550208

Pastel, R. (2011). Positioning graphical objects on computer screens: A three-phase model.,(1), 22–37. https://doi.org/10.1177/0018720810397353

Pathmanathan, N., Becher, M., Rodrigues, N., Reina, G., Ertl, T., Weiskopf, D., & Sedlmair, M. (2020). Eye vs. head: Comparing gaze methods for interaction in augmented reality., Article 50, 1–5. https://doi.org/ 10.1145/3379156.3391829

Port, N. L., Lee, D., Dassonville, P., & Georgopoulos, A. P. (1997). Manual interception of moving targets I. Performance and movement initiation.,(3), 406–420. https://doi.org/10.1007/pl00005769

Prytz, E., Montano, M., & Scerbo, M. W. (2012). Using Fitts’ law for a 3D pointing task on a 2D display: Effects of depth and vantage point.,(1), 1391–1395. https://doi.org/10.1177/1071181312561396

Qian, Y. Y., & Teather, R. J. (2017). The eyes don't have it: An empirical comparison of head-based and eye-based selection in virtual reality., 91–98. https://doi.org/10.1145/ 3131277.3132182

Radwin, R. G., Vanderheiden, G. C., & Lin, M.-L. (1990). A method for evaluating head-controlled computer input devices using Fitts' law.,(4), 423–438. https://doi. org/10.1177/001872089003200405

Ragan, E. D., Pachuilo, A., Goodall, J. R., & Bacim, F. (2020). Preserving contextual awareness during selection of moving targets in animated stream visualizations., Article 28, https://doi.org/10.1145/3399715.3399832

Smith, S. P., & Burd, E. L. (2019). Response activation and inhibition after exposure to virtual reality.,(4), 100010. https://doi.org/10.1016/j.array.2019.100010

Soukoreff, R. W., & MacKenzie, I. S. (2004). Towards a standard for pointing device evaluation, perspectives on 27 years of Fitts’ law research in HCI.,(6), 751–789. https://doi.org/ 10.1016/j.ijhcs.2004.09.001

Teather, R. J., & Stuerzlinger, W. (2007). Guidelines for 3D positioning techniques., 61–68. https://doi.org/10.1145/ 1328202. 1328214

Tresilian, J. R. (2005). Hitting a moving target: Perception and action in the timing of rapid interceptions.,(1), 129–149. https://doi.org/10.3758/ BF03195017

Tresilian, J. R., & Lonergan, A. (2002). Intercepting a moving target: Effects of temporal precision constraints and movement amplitude.,(2), 193–207. https://doi.org/10.1007/s00221-001-0920-9

The different characteristics of human performance in selecting receding and approaching targets by rotating the head in a 3D virtual environment

DENG Chenglong1, GENG Peng1, KUAI Shuguang1,2

(1Shanghai Key Laboratory of Mental Health and Psychological Crisis Intervention, Institute of Brain and Education Innovation, School of Psychology and Cognitive Science, East China Normal University, Shanghai 200062, China) (2Shanghai Center for Brain Science and Brain-Inspired Technology, Shanghai 200031, China)

In virtual reality (VR), rotating the head to select a moving target is common. A moving target involves two general directions, that is movement toward or away from a user; thus, knowing the characteristics difference between selecting the approaching target (interception movement) and receding target (pursuit movement) is important for designing an efficient user interface.

In this study, 17 participants (7 males; mean age = 22.5 ± 2.5 years) were given an Oculus Rift helmet-mounted display to wear and instructed to complete a task in a VR environment. They were required to position a small opaque sphere (cursor) that appeared randomly on the left or right side of the visual field into a larger half-transparent moving sphere (target) on the other side of the visual field quickly and accurately by rotating their head. The target moved randomly toward or away from the cursor horizontally, which were both at the participants’ eye height, with a depth of 3 meters. The diameter of the cursor was fixed at 4°. The initial movement amplitude (A; distance between the center of the cursor and target; 20° and 40°), the target tolerance (TT; size difference between the target and cursor; 4°, 6°, and 8°), and the target’s moving velocity (V; 0.5 m/s, 1 m/s, 1.5 m/s, and 2 m/s) were varied. The cursor movement paths were divided into three phases for analysis: acceleration, deceleration, and correction.

Results showed that the average total movement time (MT) of selecting receding targets was significantly larger than that of selecting approaching targets and the two movements performed differently under different factors. A and TT had a similar influence on the total MT for both movements, which increased as A increased and TT decreased. In contrast, V had an inverse effect on the total MT for the two movements. A large V leaded to a long total MT for the pursuit movement, whereas the total MT for the interception movement decreased as V increased. Moreover, the interception movement showed a light U-shaped relationship between the total MT and V, with the lowest point at 1.5 m/s when A was 20°. The two movements were further compared in the three phases. The outcome showed that the MT of pursuit movement was only longer in the acceleration phase and deceleration phase compared with the interception movement, while the MTs of two movements were very close in the correction phase. Moreover, the three factors had different impact on the two movements in three phases. In the acceleration phase, MT increased for the pursuit movement but decreased for the interception movement as A decreased and V increased. In the deceleration phase, although MT was positively related to A and negatively related to V for both movements, the MT of interception movement increased more quicky as A increased and decreased more quickly as V increased as compared to the pursuit movement. In the correction phase, the TT had a same impact on the MT for both movements, which decreased with an increase of TT. Moreover, the increasing V and A increased the MT for the pursuit movement, while the MT of the interception movement was not affected by both V and A. Based on the findings, a model was proposed to depict the relationship between the total MT and the three factors, which fit the participants’ performance well.

This study showed that the pursuit and interception movements had different characteristics. Selecting a receding target was more difficult than selecting an approaching target via head rotation, and A and V, but not TT, had a different impact on human performance for the two movements. The empirical findings suggested the importance of considering both movements separately when designing a user interface. The model provides a valid method for quantitatively evaluating the characteristics of human performance in selecting moving targets.

moving target, head-gaze control, movement trajectory, human performance modeling, human-computer interaction

2021-06-02

* 中国博士后科学基金项目(2019M661438), 国家自然科学基金项目(32100879, 32022031), 上海市科委基础研究重大项目(19JC1410101)和华东师范大学“幸福之花”基金先导项目(2019JK2203)资助。

蒯曙光, E-mail: sgkuai@psy.ecnu.edu.cn

B849