分布与端部激励下悬索瞬时相频特性对比
2023-01-03孙测世邓正科
孙测世, 李 聪, 邓正科, 谭 超
(1. 重庆交通大学 土木工程学院,重庆 400074; 2. 湖南城市学院设计研究院有限公司,长沙 410005)
索结构在超高压输电线、大型体育馆及大跨径桥梁中应用广泛,且多数结构以多索形式共同承载[1]。索结构是一种柔性结构,极易在外激励作用下,产生各种不同大幅振动,进而引发一系列损坏[2-4]。其中大幅振动与索间相位差引起的碰撞问题随着超高建筑、超大跨径桥梁的发展愈加突出,全球的多座桥均发生过拉索碰撞事件[5-7],给桥梁带来非常大的危害。
大振幅[8]和相位差是索发生碰撞的根源,前者是幅频特性的反映,后者是相频特性的反映。索碰撞的必要条件是相频特性差异,相频特性是指响应与激励的相位差随激励频率的变化。相关研究表明响应与激励的相位差与激励频率有关[9-10],且在多模态下,结构不同模态之间的相位差也受激励频率的影响[11]。目前,对相频特性或相位差的关注已不少,如Rega等对横向荷载作用下悬索的研究表明响应滞后于激励,其相位差与激励频率有关。Bossens等[12]进行了大规模的主动控制模型试验,他们给予悬索的主动端部振动与悬索索力的相位差也随激励频率变化。Baicu等[13]对一端施加横向激励的水平悬索进行试验,发现其相频曲线是一条具有一正一负两个峰值的曲线。Zhao等[14]进行考虑温度作用下的悬索非线性振动研究,发现其调谐相位图中存在多值。Kim等[15]的研究则表明施工过程中斜拉桥的最大悬臂端的竖向振动与斜拉索振动也有相位差存在。
可见,悬索相频特性与激励及其频率密切相关。但上述研究中的相频特性均指方程线性解中的相移值,当激励频率不变时,该相移值为恒定常数。而在非线性系统中,系统响应不仅包含其线性项,还有多个高阶近似项。当高阶项对响应的影响较大时,将使得响应相位随时间呈周期变化[16],即:系统某个瞬时的相位在逐渐变化。
分布激励和端部激励是两种典型的激励形式。为探明两种激励下悬索的瞬时相频特性的异同,本文分别建立了面内分布激励和端部激励作用下的悬索模型。采用多尺度法求解系统在不同参数下的响应,利用Hilbert变换得到瞬时相位,进一步对比分析响应的激励相位差幅值在λ2-Ω平面内的分布规律。
1 力学模型
1.1 基本假定
悬索简化模型,如图1所示。研究悬索分别在分布激励和端部激励下非线性振动的相频特性。假设分布与端部激励的激励频率大小一致,考虑到精简符都采用激励频率Ω。悬索模型中设分布激励幅值为F;端部激励面内横向激励幅值为ub,竖向激励幅值为vb,端部激励的面内横向位移Ub(t),竖向位移Vb(t),取索长l和垂度d。考虑到悬索振动方向与端部激励方向的一致性,此处仅需建立局部振动坐标系o-xy(见图 1),其中:坐标原点o为左端锚固点;x为悬索的索向坐标;y为索面内垂直索向下的坐标。另外,各方向对应位移分别用u,v表示。假设:①悬索的抗弯刚度足够小以至于可以忽略不计;②悬索只承受拉力;③悬索在振动过程中的轴向应变足够小;④只考虑几何非线性,不考虑其他非线性。

图1 水平悬索动力学模型Fig.1 Dynamic model of horizontal suspended cables
1.2 动力平衡方程
考虑悬索的几何非线性及悬索两端铰接,基于Hamilton变分原理,考虑悬索的垂度,得到运动方程。在准静态假设下,忽略u轴向加速度和速度项,即不考虑轴向振动,其后考虑边界条件得到位移u(x,t)[17],对方程进行约化可得到其面内分布激励非线性动力平衡方程[18]为
其中用到的无量纲变换如下(为书写方便*已经省略)
式中:“′”为对坐标x求导;“·”为对时间t求导;m为拉索单位长度质量;c为阻尼系数;H为拉索索力;E为弹性模量;A为截面积;y=4(d/l)x(1-x)为拉索静态构型。
同理,可得到其面内端部激励非线性动力平衡方程[19]为
其中
U(t)=ubcosΩt×cosθ-vbsinΩt×sinθ
式中,θ为拉索的倾角,但是因悬索中的倾角为0,式(2)可进一步化简只跟轴向激励有关项,即
U(t)=ubcosΩt
1.3 离散化模型
1.3.1 分布激励
分布激励下振动模型如图 1(a)所示,已知悬索边界条件为
v(0,t)=0,v(l,t)=0
在分布外激励作用下,悬索振动位移被认为是由纯模态振动产生,因此令
(3)
式中:Φk为悬索第k阶振动模态;qk为悬索面内振动的第k个广义时间坐标。其第k阶面内正对称和反对称模态函数[20]为
(4)
式中,h为附加索力轴向分力。
利用Galerkin方法可得
其中
1.3.2 端部激励
端部激励下振动模型如图 1(b)所示,已知悬索边界条件为
v(0,t)=0,v(l,t)=Vb(t)
端部激励作用下,悬索振动位移被认为是由纯模态振动与静位移产生,因此令
(6)
利用Galerkin方法进行模态截断得到
(7)
其中
Δ=2A(t)+L2(t),A(t)=U(t)=ubcosΩt,

2 摄动分析
2.1 分布激励
基于多尺度法求得近似解并令其为
q(t,ε)=εq0(T0,T1,T2)+ε2q1(T0,T1,T2)+ε3q2(T0,T1,T2)
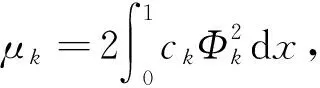
(8)
(9)
(10)
可解得式(8)近似解为
q0=A1(T1,T2)exp(iωkT0)+cc
(11)
将式(11)代入式(9),同时令长期项为零[21]
D1A=0
(12)
可解得
(13)
其中
将式(13)和式(11)代入式(10)得到关于q2的长期项

式(5)的二阶近似解为
q=εacos(Ωt-γ)+
(16)
2.2 端部激励
同理采用多尺度法求解端部激励下面内振动微分方程。按照ε的幂次进行整理,得面内方程。
(17)

(18)
(19)
可解得式(17)近似解为
q0=A1(T1,T2)exp(iωkT0)+cc
(20)
将式(20)代入式(18),同时令长期项为零得到[22]
-2iωkD1A1+feiσT1=0
(21)
式中,f为与端部激励相关的项
且得到高阶近似项为
(22)
将式(20)和式(22)代入式(19)得到q2的长期项
(23)
同理,结合式(21)与式(23),可得平均方程

式(7)的二阶近似解为
q=εacos(Ωt-γ)+
(25)
3 数值分析
为研究在漂移项及高阶项存在的情况下悬索相频特性,利用MATLAB软件对悬索在分布激励和端部激励下进行数值分析,取索参数如表1所示。

表1 索参数[23]Tab.1 Cable parameters
3.1 分布激励
3.1.1 时程曲线
为使结果一般化,取无量纲分布激励频率Ω=1.0,激励幅值F=0.01。参照以往理论的取值范围,然后从小到大依次取索力为5 500 kN,6 500 kN,7 500 kN,8 500 kN和9 500 kN,相应的垂跨比为0.013 1,0.011 1,0.009 6,0.008 5,0.007 6。为使结果更具有一般性和代表性,引进与垂跨比相关的λ2参数。图 2中给出与上述5组垂跨比对应的λ2值5.07,3.91,3.07,2.68,2.00,并且绘画出相关λ2值悬索的响应时程曲线。
从图 2(a)中可以看出在λ2为2.68,2.00时的响应时程曲线比较接近,并且不难发现,图 2中各λ2下时程曲线均存在向下漂移,这是因为近似解中的漂移项所引起的。对比图 2(a)中各λ2下时程曲线线型,可明显观察到当λ2=5.07和λ2=3.91时,时程曲线下波峰线形发生变化。图 2(a)中λ2=2.68,λ2=2.00和λ2=5.07,λ2=3.91的曲线相比,后两个λ2的曲线下波峰段较为平缓。在图 2(b)λ2=3.07时响应曲线线型变化更为明显,时程曲线整体下移至负轴,下波峰段向上突起,这是因为这3个λ2参数下的二倍频项对悬索振动响应产生较大影响所致。

图2 不同λ2下的时程曲线图Fig.2 Time history curves for different λ2
当时程曲线线型发生改变,瞬时相位也会受到影响。因二倍频项在λ2=5.07和λ2=3.07下对悬索振动响应产生不一致的影响,为进一步分析原因,分别对其的响应与激励的时程曲线进行Hilbert变换得到瞬时相位,再对同一时刻的响应瞬时相位与激励瞬时相位做差得到响应与激励的瞬时相位差值。考虑差值在[-π, π]变化,以无量纲时间为横坐标,瞬时相位差为纵坐标,绘制出如图 3所示瞬时相位差的时程曲线。

图3 瞬时相位差时程曲线Fig.3 Instantaneous phase difference time histories curve
为求得响应瞬时相位,且体现其一般性,定义无量纲参数为
(26)
式中,Δp为拉索响应瞬时相位与激励瞬时相位之差。
瞬时相位差时程曲线的周期与时程曲线的周期相同。由图 3可知,响应与激励瞬时相位差随着时间不再是一个定值,这是受近似解中二倍频项与漂移项的影响。当λ2=5.07时,瞬时相位差波动峰值仅为0.26,且变化波形较为平缓;当λ2=3.91时,峰值接近0.96,即瞬时相位差值接近π,同时峰值附近瞬时相位差具有明显突变。图 3中的瞬时相位以原平衡位置为基准,瞬时相位差较大值出现在上波峰处,由于漂移项的影响使得响应与激励的振动中线分离,从而进一步导致瞬时相位差的增大。
通过求解空间点的运动轨迹来获得悬索的运动情况,取图 2中较为典型的3个不同的λ2参数,这3个参数具有较大的差距时程曲线,即对λ2=3.91,λ2=3.07和λ2=2.68的q(t)进行Hilbert变换。通过绘制复平面图和瞬时相位差幅值的时程曲线图来分析激励与响应的瞬时相位差的变化特性以及最大瞬时相位差的原因,如图 4所示。

图4 复平面图及瞬时相位时程图Fig.4 Complex plane diagram and instantaneous phase time histories graph
对应点随着时间的变化绕着响应曲线转动,瞬时相位具有周期性。图 4(a)为λ2=3.91的复平面图及瞬时相位差时程曲线图,由于响应振动存在较大的漂移,从而使得响应投影曲线向左移动,进而引起瞬时相位差的产生。如图 4(b)所示,当λ2=3.07时复平面图中响应投影曲线左端出现小“圆环”,对应着响应时程曲线的下波峰,可见这是受二倍频的影响,当二倍频系数越大,小“圆环”越明显。同时响应投影曲线向左平移至二三象限使得响应与激励的瞬时相位在右端点上产生较大的相位差,瞬时相位差时程曲线出现突变点。如图 4(c)所示,当λ2= 2.68时,最大瞬时相位差小于0.2π,可见此参数下响应与激励不会产生较大的瞬时相位差。
3.1.2 最大瞬时相位差的分布
为便于进一步对p的幅值进行研究,再定义一个新的无量纲参数
(27)
式中,Δpmax为悬索响应瞬时相位与激励相位之差Δp的幅值。后续分析中均考察pmax的分布规律用以讨论不同参数下的悬索的瞬时相频特性。
采用MATLAB软件对悬索在分布激励下的主共振响应进行数值分析。通过改变悬索的λ2与激励频率Ω获得对应的时程数据,其中λ2变化范围为1~6,间隔为1.0;激励频率Ω的变化范围为0.90~1.35,间隔为0.01。对不同参数下的时程数据和激励时程数据分别进行Hilbert变换来得到两者的瞬时相位差。
图 5为分布激励下最大相位差pmax在λ2-Ω平面内分布的等高线图。其中,图 5(a)为λ2在1~6内的整体图像,图 5(b)为λ2在2.81~3.37内的局部放大图,为保证图像的准确性,数值计算时对点进行了加密计算。由整体图可知,pmax在λ2≈3.0的狭小区间内有突变,数值接近1,即相位差接近π;而在其他区间pmax数值均在0.5以下。由局部放大图可知,等高线图以λ2=3.06为界,其左右两边的pmax变化趋势大致成反对称分布。当λ2<3.06时,同一λ2参数下pmax随Ω增大而增大;而在λ2>3.06时,变化趋势相反。另外,由局部放大图还可看出,pmax接近1的区域会随λ2和Ω的关系而变化,大致以Ω=-0.96λ2+4.06和λ2=3.06两条直线的交点为中心(对应Ω=1.12),沿Ω=-0.96λ2+4.06逐渐变宽。

图5 分布激励下λ2-Ω平面内的pmax等高线图Fig.5 pmax contour map in λ2-Ω plane under external excitation
为更清楚的进行对比,取Ω=0.95,1.10和1.25时pmax随λ2参数的变化曲线绘于图 6。由图 6可知,3种激励频率Ω下Pmax在λ2=3.06附近时均突然增大,且其峰值随Ω增大而往λ2负方向移动。

图6 分布激励作用下的pmax-λ2曲线Fig.6 pmax-λ2 curves under external excitation
3.2 端部激励下的最大瞬时相位差
类似的,对端部激励下的时程数据进行Hilbert变换,得到最大瞬时相位差随λ2及激励频率Ω的变化曲线图,如图 7所示。相比分布激励,端部激励下的pmax在λ2-Ω平面上的所有区域内的数值均较小,其最大值仅约为0.3,且仅集中出现在λ2≈3.0且Ω≈1.12附近的很小区域内。将λ2在2.59~3.39的区域加密再局部放大,得到右侧的局部放大图如图 7(b)。可见,pmax≈0.3的区域很小。pmax的等高线图变化趋势也大致关于λ2=3.06呈反对称分布。
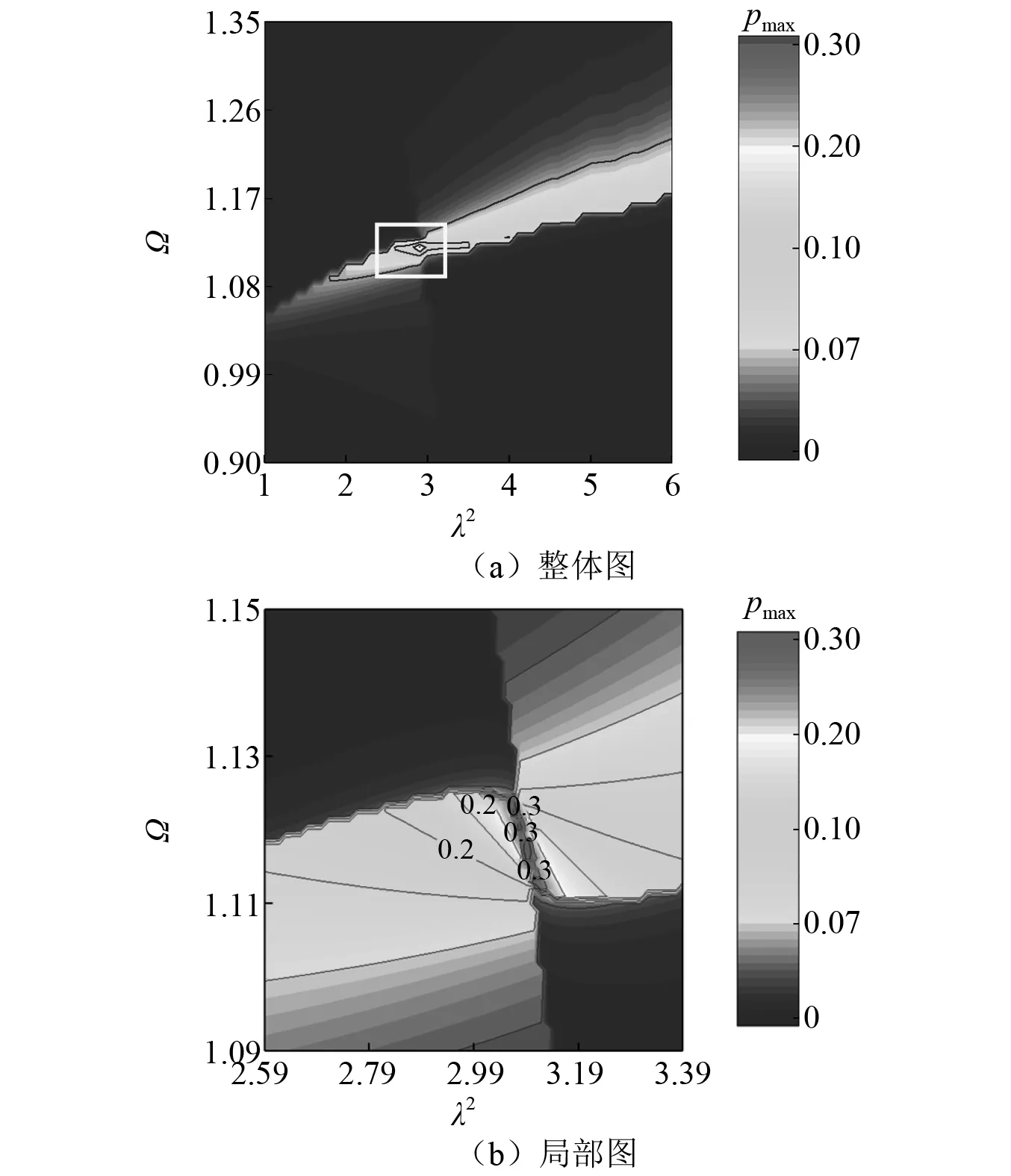
图7 端部激励下λ2-Ω平面内的pmax等高线图Fig.7 pmax contour map in λ2-Ω plane under end excitation
图 8为无量纲端部激励频率为1.00,1.12和1.27时的瞬时相位差幅值随λ2参数的变化曲线。由图 8可见,仅在激励频率Ω=1.12的pmax曲线出现突增,峰值接近0.3,其他激励频率下pmax数值变化较小,最大值不超过0.1。
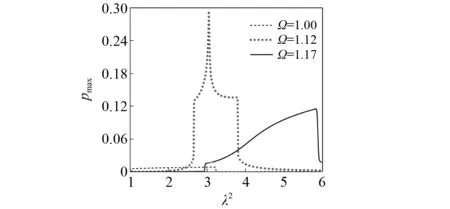
图8 端部激励作用下的pmax-λ2曲线Fig.8 The pmax-λ2 curves under end excitation
3.3 对比分析
从以上pmax的等高线图来看,无论分布激励还是端部激励,在λ2-Ω的参数平面内,响应与激励的瞬时相位差幅值均会在λ2≈3.0附近某一个狭小的区域内发生突变,且从局部看均存在反对称分布规律。不同之处在于,分布激励下pmax整体上大于端部激励下的情形,前者最大值约为1,后者最大值仅为0.3;前者分布于λ2≈3.0的一个狭长的带域附近,而后者分布在λ2≈3.0且Ω≈1.12的一个点域附近。另外,结合等高线图和pmax-λ2曲线图还可以看出,悬索受不同类型激励作用时,激励频率变化对瞬时相位差产生的影响并不同。
从解析式表达式来看,分布激励和端部激励的近似解式(16)和式(25)的形式是一致的,导致两者响应及其相位差不同的原因是:分布激励和端部激影响了长期项的形式,从而导致响应幅值的变化。这可以由式(12)与式(21)看出,式(21)中多了与端部激励相关的项feiσT1;同时,式(14)与式(23)对比,式(14)中多出0.5FeiσT1一项。因此,分离实、虚部后的方程不同。得到的频率响应方程式(15)和式(24)虽在结构上类似,但右边项不同,所以响应振幅a不同,导致高阶近似解的漂移项和二倍频项不同,进而出现不同的相频特性。
3.4 讨 论
(1)瞬时相频特性本质上是非线性效应对系统固有频率的调制作用,即:系统非线性固有频率随时间变化,因而响应的频率并非时时等于激励频率,体现为“瞬时”性和“周期”性。
(2)瞬时相频特性对时间的一阶导数,便是瞬时频率,而后者与悬索瞬时索力间存在确定性关系。因此,两种类型激励下,悬索瞬时相频特性pmax在λ2-Ω平面内分布上的差异,可能对其动态最大索力的研究有借鉴意义,值得后续开展深入研究。
(3)由于瞬时相频特性是各个时刻相位的真实反映,因此其也是研究斜拉桥等结构中具有相近参数拉索间的相对运动的基础。
4 结 论
(1)考虑高阶近似项的影响后,响应与激励瞬时相位差不再是与时间无关的定值γ,而是随时间成周期变化。
(2)瞬时相位差产生的原因,一是漂移项导致复平面偏移,从而影响瞬时相位差最大值;二是二倍频的存在导致复平面曲线圈线形发生改变,从而影响瞬时相位变化规律。
(3)悬索在分布激励与端部激励作用下,响应与激励的瞬时相位差幅值pmax均会在λ2≈3.0且Ω≈1.12为中心的局部范围内突然增大,且近似在λ2-Ω平面内呈反对称分布。但是,前者突变的范围呈现在λ2≈3.0的狭长带域内,而后者集中在该中心点附近。另外,量值上分布激励下的pmax约为1,而端部激励下仅为0.3。
