有轨电车转向架轴桥装置振动特性分析

□ 任春吉 □ 陆亚龙

中铁二局集团新运工程有限公司 成都 610036

1 研究背景

有轨电车转向架系统内部结构较复杂,考虑到低地板结构,动力转向架通常采用独立旋转车轮耦合驱动结构,提高转向架整体导向性[1]。有轨电车内部动力转向架传递振动并搭接传动系统与车体的部件为动力轴桥,通常布置在转向架构架侧面,多采用架悬方式,实现车轮的独立转动[2]。动力传递路径为电机、联轴器、输入齿轮轴、输出齿轮、输出联轴节、车轮[3]。为了提高电车性能和舒适度,有轨电车逐渐出现低地板化的趋势,现如今我国常见的有轨电车地板面距离地面一般不超过400 mm[4]。

轨道随机不平顺属于轨道典型的不确定性激励,具有较悠久的研究历史。罗林[5]在研究轨道不平顺测量时,提出了惯性基准法并进行大量实测,列举了平稳轨道下的功率谱密度样本。陈果等[6-7]在模拟轨道不平顺时域样本时,采用频谱功率谱的等效算法求出了不平顺功率谱随机相位,提升了时域样本精度,之后基于我国高速铁路无砟轨道总结了轨道不平顺平均谱拟合系数。

国外学者对轨道不平顺功率谱函数也进行了针对性研究。Ontes等[8]提出二次滤波法来实现轨道不平顺的时频转换,设计出合理滤波器,得到理想状态下的不平顺时域样本。Garg等[9]将线路不平顺拟合成以截断频率表示的偶次函数,并归纳轨道表面粗糙度参数列为美国标准轨道谱参数。Sadeghi等[10]从波长的角度分析了振幅对平顺性的影响,研究表明,轨道不平顺波长小于0.75 m时,铁路线路的乘坐舒适性显著降低,为轨道不平顺幅值研究提供参考依据。

关于转向架外部激励的研究内容虽然悠久,但具有一定单一性,鲜有综合考虑轮轨间激励、轨道激励等外部激励,以及齿轮系统内部激励对动力转向架轴桥振动特性的影响。笔者以某型号低地板有轨电车动力转向架轴桥为研究对象,开展针对轴桥装置外部轨道激励及齿轮系统内部激励的分析,在此基础上进行动力转向架轴桥装置振动特性响应的相关研究[11-12]。

2 动力转向架结构

动力转向架结构如图1所示,某型号低地板有轨电车将牵引电机放置在转向架一侧,有轨电车一节车体配置有两部分轴桥装置,其中电机牵引实现车轮转动的轴桥装置称为动力转向架轴桥。轴桥装置的传动系统置于动力轴桥壳体内,由多级平行轴传动组成,采用的齿轮模数、材料均相同。由于车轮通过轴桥直接连接,转向架高度能够保证与地面的距离不超过400 mm,车轮部位高度基本与轴桥装置齐平,实现车体内部低地板占有量达到100%。

图1 动力转向架结构

3 轨道高低不平顺激励分析

3.1 轨道激励

轨道激励是造成低地板有轨电车振动的重要来源之一,轨道激励通过轨道依次传递至车轮、动力轴桥、转向架,以及车体。其中非确定性激励主要指轨道的几何随机不平顺,几乎会一直伴随着有轨电车的行进而存在。这种振动由轴桥装置传递至转向架整体,长期会造成车体振动加剧,影响乘客乘坐舒适度和物品运送的平稳性,严重时会造成轨道线路的变形积累,造成轨道几何形状的恶化。

轨道高低不平顺如图2所示。左右轨道顶面法向偏移引起轨道中心线法向偏移,使得有轨电车行进过程中轮轨间垂向作用力激增,是造成行驶过程中车体颠簸的主要原因。

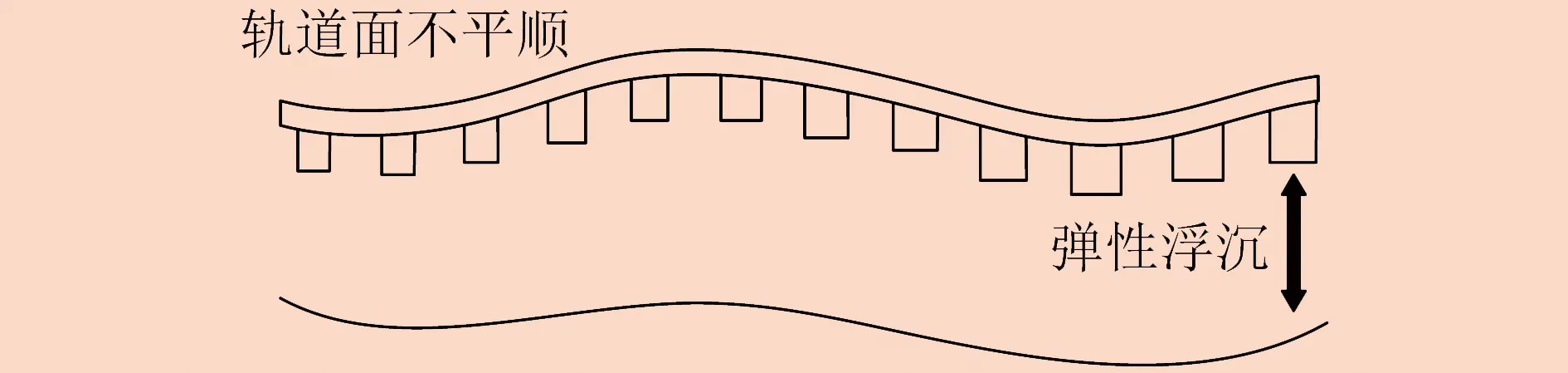
图2 轨道高低不平顺

3.2 轨道高低不平顺时域模拟

通过长期试验,以及与国外轨道谱的对比,我国一般干线铁路线路几何状态即常态,轨道的不平顺功率谱密度函数S(f)可表示为:

(1)

式中:f为空间维度频率;A、B、C、D、E、F、G为功率谱密度函数的特征参数,取值见表1。

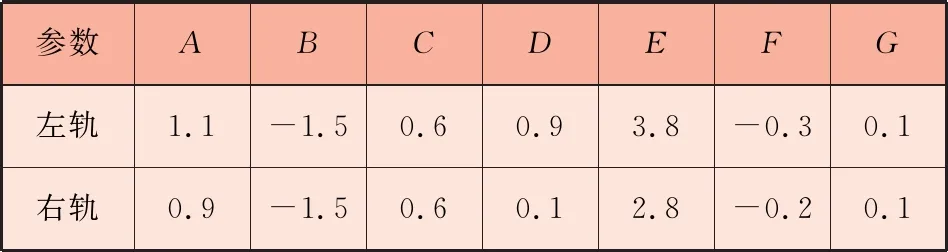
表1 轨道功率谱密度函数特征参数

设功率谱密度函数S(f)在离散点的功率谱密度函数表示为Sx(f),那么功率谱密度函数与离散点频谱关系表示为:

(2)

式中:X(f)为离散点的时间序列频谱;X*(f)为常态时间序列频谱;Nc为空间计算频率;xs为第s个采样频率;xj为第j个采样频率。

在进行时频转换之前,先将功率谱密度函数转换为双边谱密度函数Sk(f),并将时间序列用[Xt]表示。设采样总时间为Tz,采样周期ΔT,则采样点数Nr为:

Nr=Tz/ΔT

(3)

离散点的时间序列频谱的模值|X(f)|为:

(4)

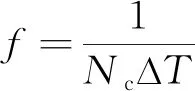
(5)

式中:Δf为空间维度频率的分量。

随机性是时间序列频谱相位具备的特征,这里设相位为ξn,考虑到实序列的快速傅里叶变换为复序列,则ξn为复数,于是有:

ξn=cosφn+isinφn=exp(iφn)

(6)

φn为复数域中的旋转因子,在0～2π的范围内均匀分布。

时间序列[Xt]的实部在Nc/2处满足偶对称,在计算过程中只考虑离散点时间序列在0～2π范围内的频谱,结合式(4)和式(6),可以得到:

(7)

计算过程中,只需将式(7)在MATLAB软件中进行傅里叶逆变换,得到轨道不平顺时域模拟样本曲线,可将高低不平顺的时域激励信号转化为轨道与车轮侧面接触区域处的法向作用力F(f),表达式为:

F(f)=[Xω(f)/G]3/2

(8)

Xω(f)为经过傅里叶逆变换后的轮轨高低不平顺时域激励信号,即两车轮与轨道之间的弹性变形量。G为轮轨赫兹非线性弹性接触常数,G的数值与车轮踏面的结构形状有关。当车轮为倾斜锥型踏面时,G为:

G=4.57×10-8R-0.149

(9)

式中:R为车轮的实际滚动圆半径。

3.3 轨道高低不平顺模拟结果

基于上述方法,已知型号的有轨电车最高行驶车速为80 km/h,其它工况信息为:额定输入转速为2 600 r/min,负载转矩为440 N·m,额定功率为120 kW,通过表1选取左、右轨道的特征参数并代入到式(1)中,计算得到有轨电车匀速运行10 s的高低不平顺位移响应,如图3所示。

图3 高低不平顺位移模拟

由图3可以看出,轨道沿高低方向的波动幅值在-2～2 mm范围内变化,不平顺程度具有一定的波动性,但波动程度相对稳定。

有轨电车在行驶过程中转向架车轮部位会受到随机的法向力,根据模拟的时域激励信号,由式(8)得出有轨电车行驶过程中轮轨受到的法向力,如图4所示。

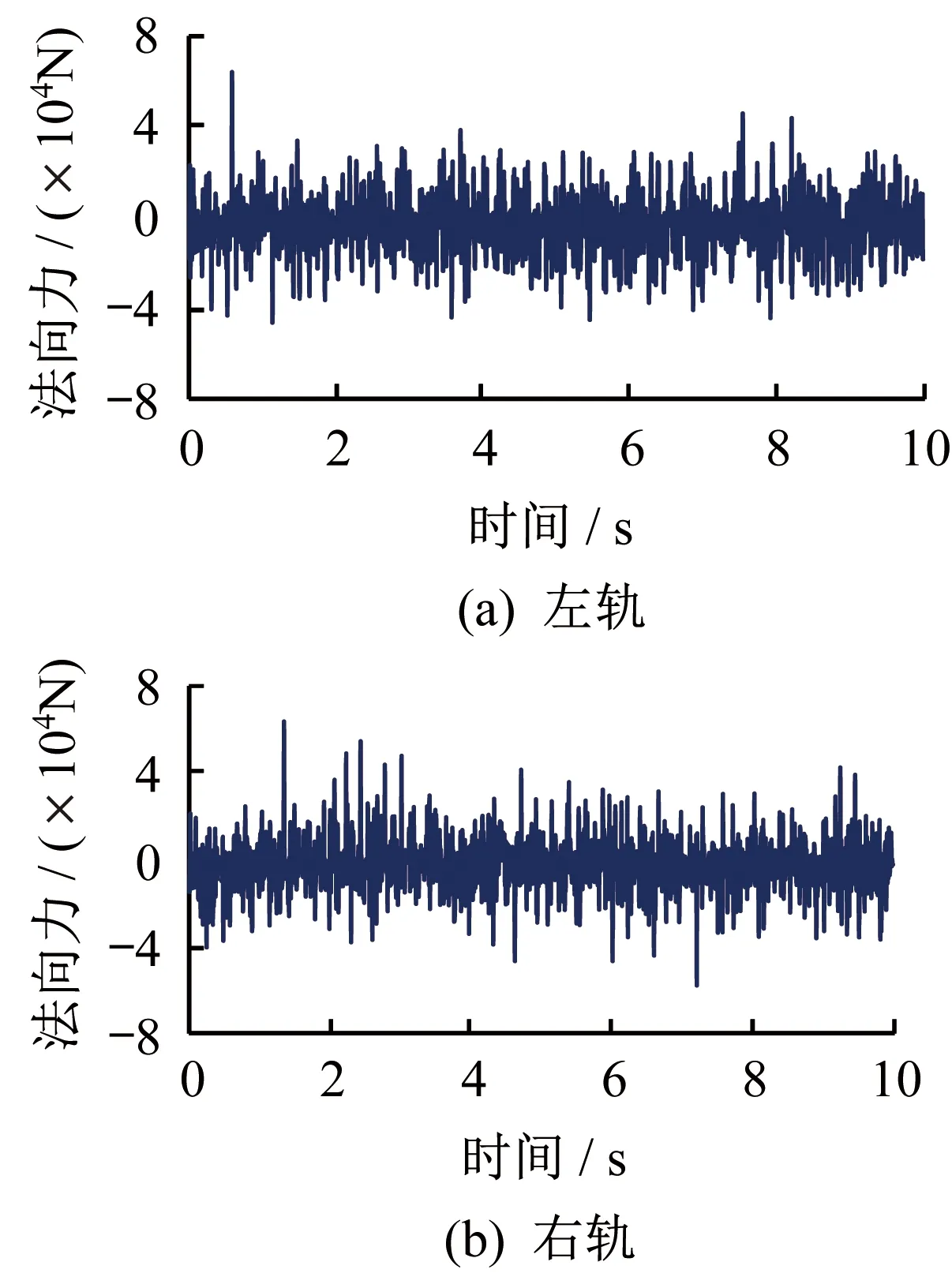
图4 轮轨法向力

由图4可以看出,两侧车轮在运行时间内受到的轮轨法向力波动范围集中在-40～40 kN内,没有出现较大偏差,几何状态较好。

轮轨法向力能影响动力轴桥的垂向振动,将左、右两侧车轮的轮轨法向力进行平顺优化处理,消除波动较大数值,再经由傅里叶变化得到轮轨法向力频谱,如图5所示。

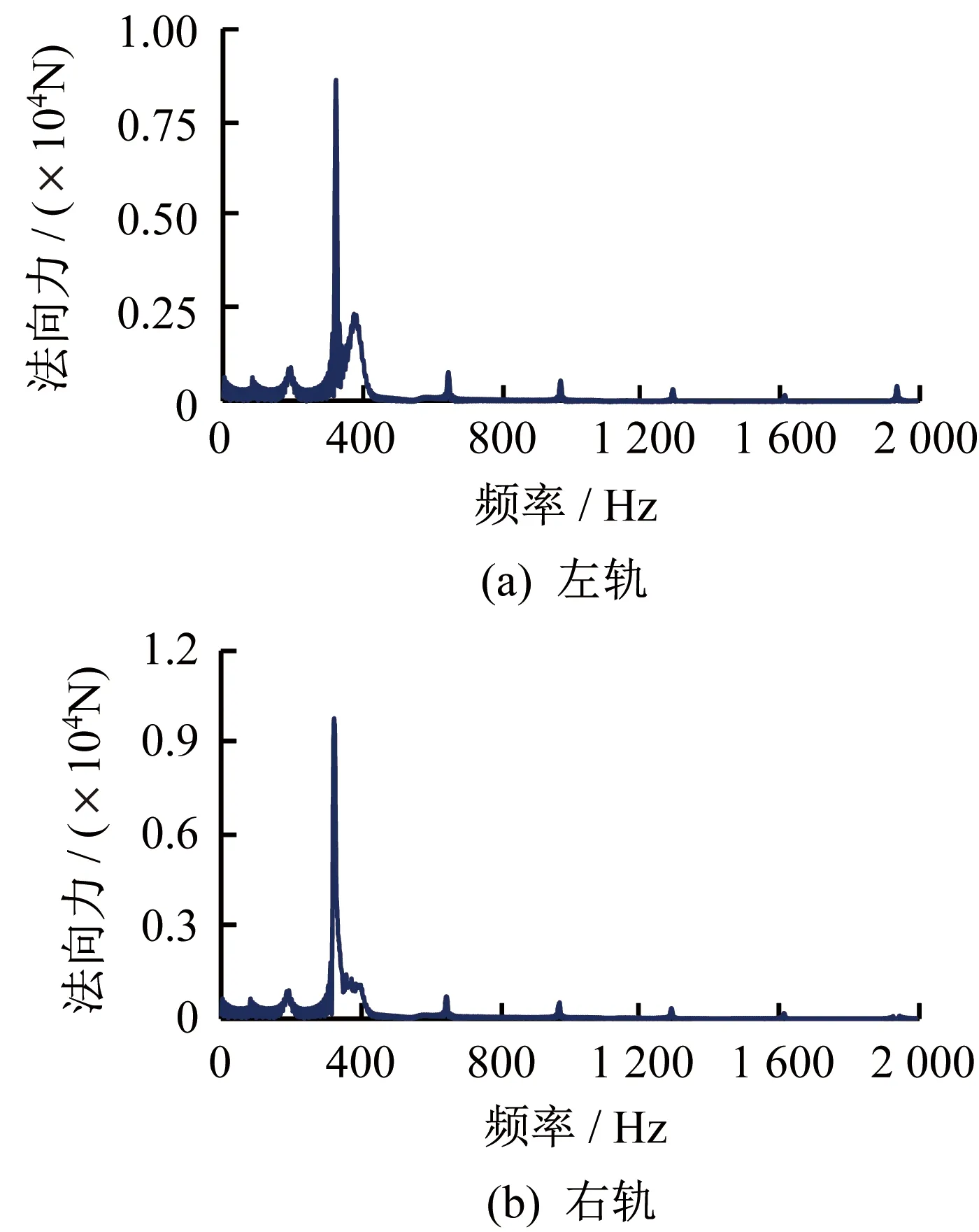
图5 轮轨法向力频谱

由图5可以看出,轮轨接触运动时,法向力在中低频附近约323 Hz出现峰值,且在其倍频处也能看到较小但有明显的幅值,证明轨道不平顺激励中垂向不平顺在中低频段会对轮轨接触产生较大的影响,将出现峰值处的频率视为轮轨间的振动频率。

4 动力转向架轴桥振动响应分析

基于ANSYS软件编写APDL加载程序,将齿轮系统动态啮合力施加在齿轮啮合线附近的节点上。确定约束及载荷边界条件后,采用模态叠加法计算轴桥装置振动响应,建立动力转向架轴桥有限元分析模型如图6所示。

图6 动力转向架轴桥有限元分析模型

为验证内、外部激励下的轴桥装置振动特性,在动态啮合力的基础上考虑轨道不平顺激励,分析啮合力对动力转向架轴桥振动特性的影响程度,并在计算完成后选取动力转向架轴桥外部壳体上六个节点作为响应结果评价点,如图7所示。

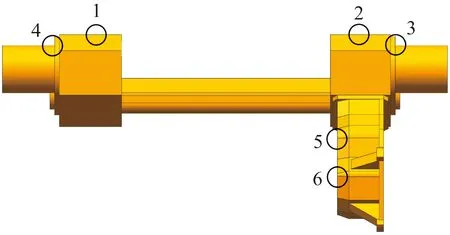
图7 动力转向架轴桥振动响应评价点

各节点无外部激励时计算结果整理见表2。

表2 无外部激励时振动加速度均方根值

同理给出考虑外部激励的结果,整理见表3。

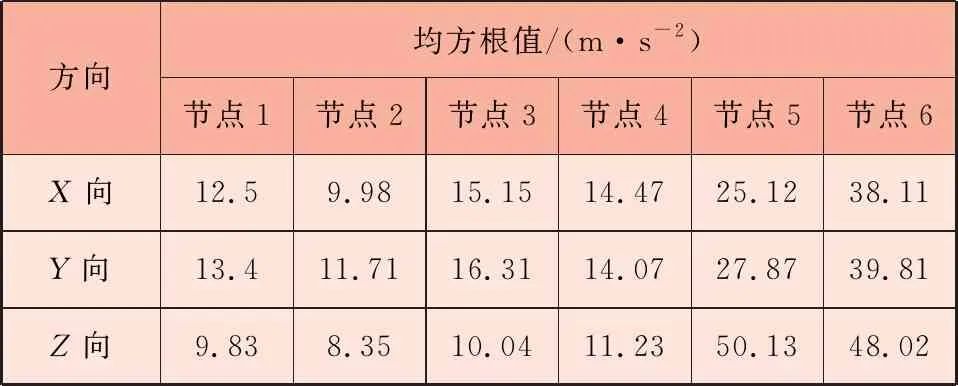
表3 有外部激励时振动加速度均方根值

从表2、表3中数值变化可以看出,受到外部激励影响时,各评价点的振动加速度均方根值均有所增大,且左右两侧输出端即节点3和节点4的增幅较明显,主要原因是外部激励作用位置集中在输出端,而输出端受轮轨法向力作用的Z方向的加速度响应增幅最明显。

为了更好地研究观察外部激励影响下评价点振动响应的变化,分别给出不同激励条件下输出端节点4法向振动加速度结果的时域、频域图对比,如图8、图9所示。

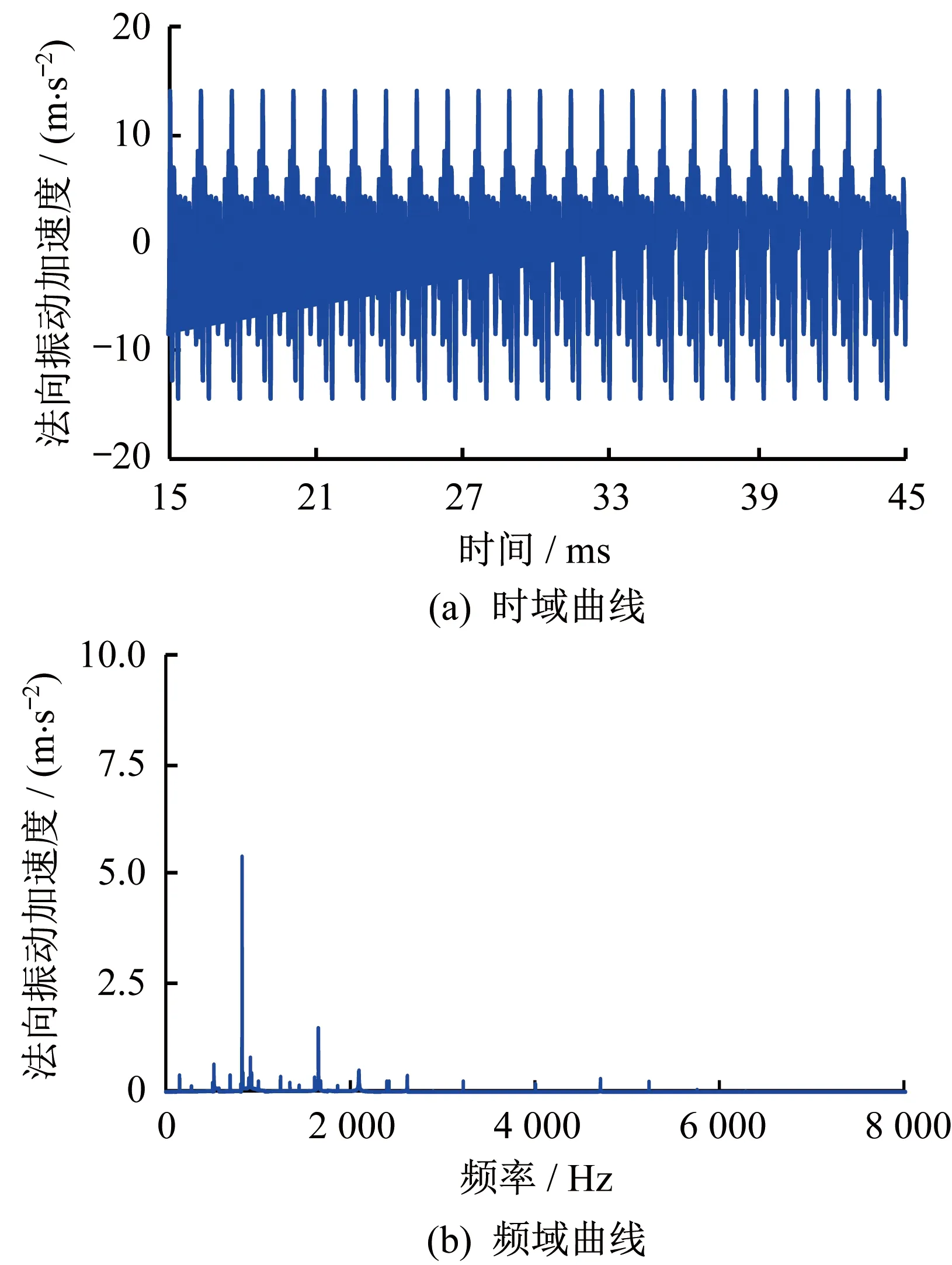
图8 无外部激励时节点4 Z向振动响应时频曲线

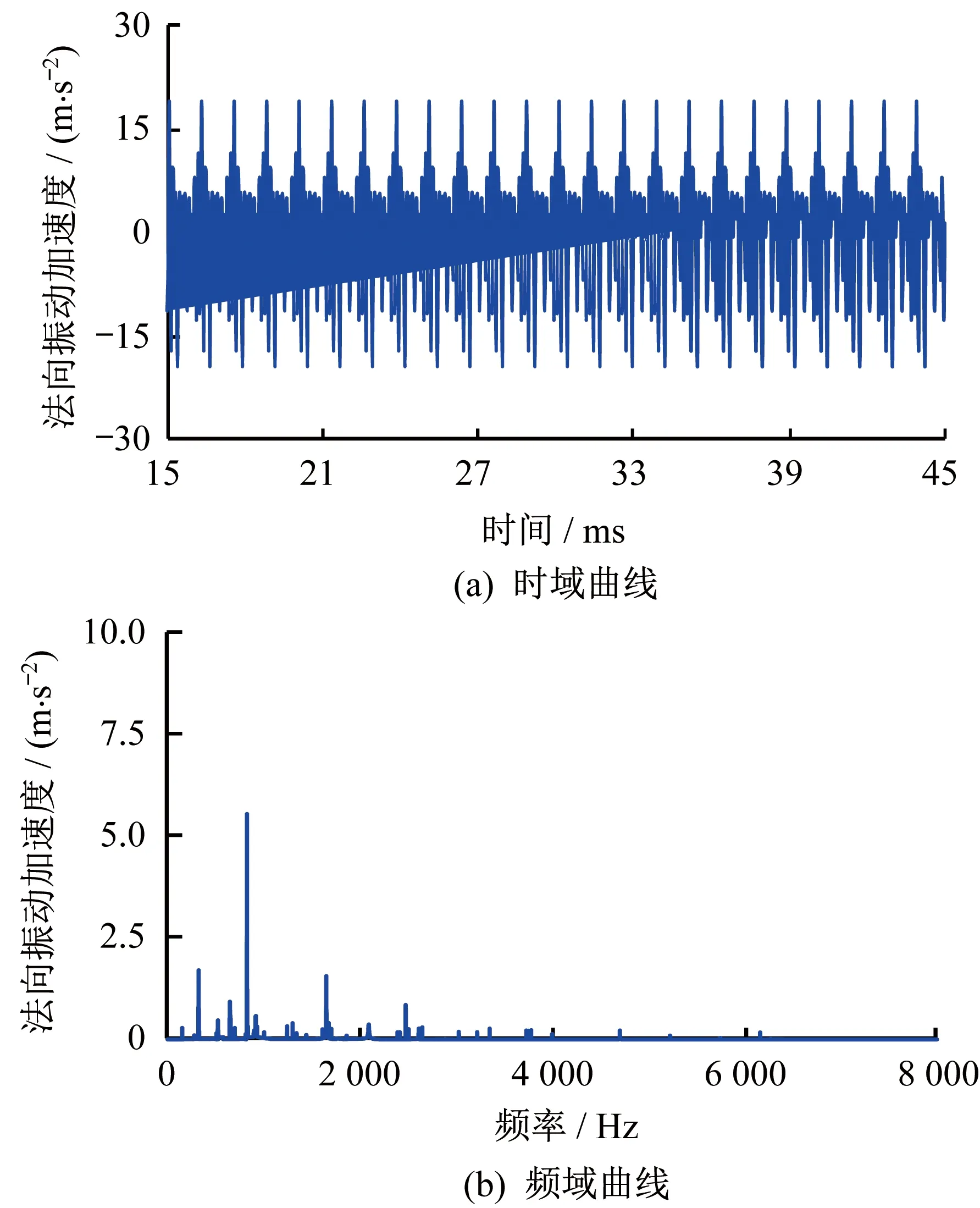
图9 有外部激励时节点4 Z向振动响应时频曲线

由图8、图9可以看出,系统振动规律基本保持一致,当受到外部轮轨激励影响时,低频附近变化不明显,而在300～500 Hz的中低频段附近频率更加丰富,且323 Hz附近呈现明显幅值,反映了轮轨间赫兹弹性接触的频率振动,以及轮对在外部激励作用下的整体弹性振动。

5 结束语

笔者通过对轨道功率谱密度函数的推导,得到轨道离散点不平顺时域序列频谱,计算得出在最高行驶速度下的轨道法向位移并转换为轮轨法向力。结果表明轨道高低不平顺产生的轮轨法向力在中低频约323 Hz附近出现峰值。考虑外部激励时,转向架轴桥装置输出端处节点3和节点4的振动响应明显增大,在中低频约323 Hz附近法向振动加速度幅值更加丰富,在轨道高低不平顺的作用下出现中低频车轮与轨道的耦合振动。