基于时变Markov状态转换的Realized GARCH族模型及其对期货波动率的预测
2023-01-02吴志敏蔡光辉
吴志敏,蔡光辉
(浙江工商大学统计与数学学院,浙江杭州 310018)
§1 引言
金融市场资产波动率是投资者和决策者进行风险管理,资产定价和投资组合的基础.由于金融数据存在异方差性和波动集聚等特征,波动率的建模和预测效果往往不尽人意.Bollerslev提出的GARCH模型能够较为精准地刻画上述特征,是最常见的波动率模型[1].然而,经典的GARCH族模型是基于日频数据或者更低频率的数据建立的,无法捕捉金融资产的大量日内交易信息.随着信息技术的发展,高频数据的可得性越来越高,其包含的大量交易信息能够帮助投资者做出更加合理的决策.因此,基于高频波动率模型对金融资产波动率进行研究已经成为了近几年的学术热点.
为利用高频数据衡量资产波动率,Andersen等[2]构建了对市场微观噪声较为稳健的已实现波动率测度(realized volatility,RV),该测度能够描述资产收益率的波动情况.由于其具有计算简便的特点,越来越多的学者以此为基础提出了一系列基于高频数据的波动率模型,如Engle和Gallo[3]的MEM模型,Shephard和Sheppard[4]的HEAVY模型以及Corsi[5]的HARRV模型.由于HAR-RV模型结构较为简单,越来越多的学者在该模型中考虑杠杆效应,跳跃测度和门限效应等特征以提升波动率的预测能力[6-11].
除此之外,借鉴GARCH模型的优良结构,Hansen等[12]提出了Realized GARCH模型,该模型通过在测量方程引入一个外生变量实现了隐含波动率与已实现波动率测度的联合建模.实证研究表明,Realized GARCH模型的波动率预测能力优于传统的GARCH模型.此外,与MEM模型,HEAVY模型相比,Realized GARCH模型的结构较为简洁,且收益率拟合效果和波动预测效果最佳.与HAR-RV模型相比,Realized GARCH模型能够反映资产收益率波动与已实现测度的内在联系,且考虑了金融市场的杠杆效应,从而能够更为灵活地刻画资产收益率的波动过程.因此,对Realized GARCH模型进行拓展已成为金融资产波动率研究的重点内容,具体见文[13-20].由以上可知,大多数学者围绕厚尾分布,长记忆性和已实现波动率测度等方面对Realized GARCH模型进行研究.
然而,Granger和Ding[21]研究发现,波动率的持续性并不是固定不变的.有研究[22-25]显示政府的经济政策和金融监管机制等诸多因素会使波动率的持续性存在结构突变[26-27]或在不同状态间切换[28]等特征,因此在高频波动率模型中考虑波动率的非线性结构显得十分必要.由于HAR-RV模型结构简单,其能够刻画金融市场的长记忆特征和多尺度行为,因此不少学者将HAR-RV族模型与能够捕捉波动率非线性结构的Markov状态转换机制相结合以提高波动率的预测精度[26,29-30].然而,国内外关于在Realized GARCH模型中考虑Markov状态转换机制的研究十分有限.
近年来,基于高频数据的波动率预测研究主要集中在股票,证券和期货市场.沪深300股指期货作为重要的金融衍生工具,分析其内部特征能够为股票投资者和管理者进行风险管理提供重要保障,也为资本市场的长期发展奠定了坚实基础.然而国内外研究很少通过Realized GARCH模型对沪深300期货波动率及其非线性结构进行研究.故本文选取Realized GARCH模型及其扩展模型来研究沪深300期货价格波动率的非线性结构及其对波动率预测的影响,从而为投资者对股指期货的非线性结构提供进一步认识,也为政府相关政策的制定提供了理论依据.
综上,本文旨在建立基于时变Markov转换机制的MRS-Realized GARCH族模型来预测沪深300股指期货的波动率.与已有的波动率模型相比,本文提出的模型不仅刻画了隐含波动率与已实现波动率测度的内在联系,而且同时考虑了波动率的杠杆效应,跳跃以及非线性结构等显著特征.针对国内外文献关于高频波动率建模的不足,本文作出如下贡献.
第一 采用Huang和Tauchen[31]提出的显著性跳跃检验来甄别跳跃,将显著跳跃方差纳入到Realized GARCH族模型以改善波动率预测效果.
第二 将Markov状态转换机制与基于显著性跳跃方差的时变Markov状态转换机制引入Realized GARCH族模型,构建了MRS-Realized GARCH族和时变MRS-Realized GARCH族模型,以研究已实现波动率的非线性持续结构,为认识和预测沪深300股指期货波动性提供新的方法.
第三 基于滚动时间窗预测技术和Hansen等[32]提出的模型置信集来从统计学意义上评估各模型的波动预测能力,并基于不同方面对模型进行稳健性检验,为该模型的构建合理性提供了重要保障.
§2 时变MRS-Realized GARCH族模型的构建及预测检验方法
2.1 已实现波动率与跳跃测度
根据Barndorff-Nielsen和Shephard[33]的研究,金融资产收益率的二次变差为

其中rt为资产收益率,为积分波动率,为离散的跳跃方差.当跳跃不存在且采样频率△→0时,已实现波动率RVt →[r,r]t.在实际的金融波动率研究中,由于采样频率不可能无限趋向于0,已实现波动率RVt通常由5分钟的高频收益率数据得到

其中△=1/48,rt−1+j·△为第j个采样间隔的对数收益率.考虑到金融资产价格的跳跃是普遍存在的,Barndorff-Nielsen和Shephard[33]提出了对跳跃稳健的已实现双幂次变差(BPV),其定义为

其中u1=则根据二次变差理论以及RVt和BPVt的计算公式便可推得
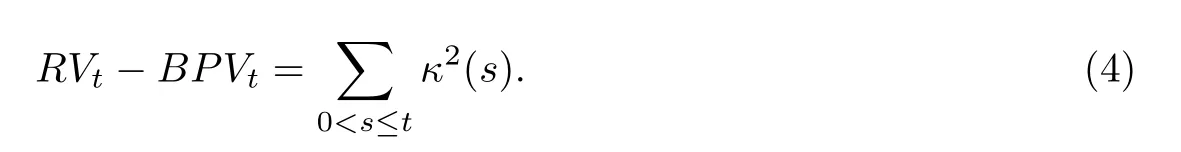
由式(1)-(3)可知,跳跃成分有正有负.为确保跳跃的非负性,Barndorff-Nielsen和Shephard[33]对跳跃成分作定义

考虑到根据式(5)提取出来的跳跃成分存在较多非零小跳跃且无法提供经济学解释,Huang和Tauchen[31]构建了显著性跳跃检验统计量
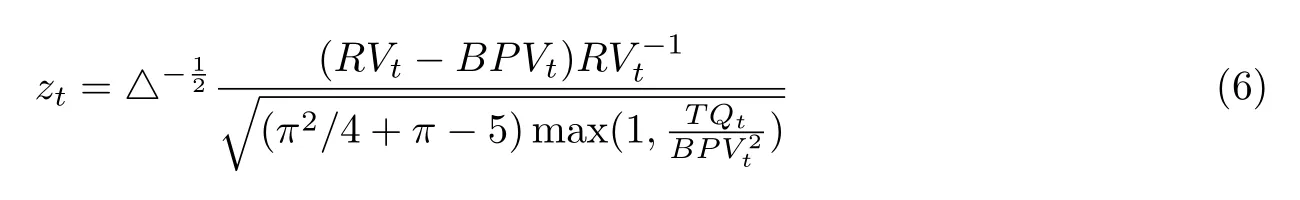
以剔除这些不显著的跳跃,其中TQt为三重次方变差,其具体的计算公式可参考[31].根据该统计量,可进一步提取出显著的跳跃方差

I(·)为示性函数,当跳跃显著即zt >φα时,I(zt >φα)=1;反之,I(zt >φα)=0.另外,φα为标准正态分布的上1−α分位数.
2.2 Realized GARCH模型
传统的GARCH模型是基于日频数据建立的,不能够捕捉大量的日内信息.针对这一缺陷,Hansen等[12]结合GARCH模型能够刻画金融资产对数收益率的波动特征和已实现波动率测度RV能够反映日内高频信息的优势,提出了Realized GARCH模型如下.
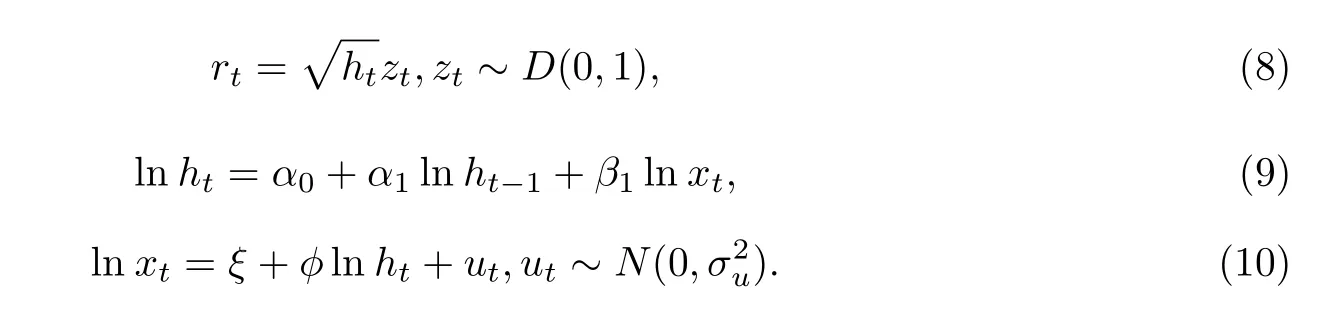
其中rt=100×ln(Pt/Pt−1)为对数收益率,Pt为第t个交易日的收盘价,zt为残差扰动项,ht为隐含条件波动率,xt为已实现波动率测度,ut为噪声扰动项.式(8)-(10)可分别记为均值方程,波动率方程,测量方程1考虑到本文基于Markov状态转换机制的Realized GARCH族模型的参数过多,增加了参数估计的复杂性.故为简便起见,在Realized GARCH族模型的测量方程中不考虑杠杆函数..Hansen等[12]的研究表明,相比于传统的GARCH模型,引入已实现波动率测度的Realized GARCH模型具有更好的预测精度,因此越来越多的学者致力于该模型及其拓展模型的研究.
2.3 Realized GARCH模型
为了能够更加灵活地捕捉收益率和波动率的联系,Hansen和Huang[34]在波动方程中引入杠杆函数,提出了Realized EGARCH模型如下.

杠杆函数δ(zt−1)=d1min{0,rt},这种设定有助于研究滞后负收益率对未来收益率波动的影响2通过实证发现Hansen和Huang[34] 设置的杠杆函数δ(zt)= d1zt +d2( −1)中的系数d2并不显著,故本文借鉴结合杠杆函数构建LHAR模型[8-9]的思想,在波动方程中引入这种新的杠杆函数结构以提高模型的参数拟合效果..实证研究表明,Realized EGARCH模型的样本内拟合和样本外预测效果优于Realized GARCH模型,故不少学者基于该模型对高频数据波动率展开了一系列研究[19,35].
2.4 基于Markov状态转换机制的时变MRS-RealGARCH族模型
由马锋等[26],Ma等[30],Pan等[36]以及蔡光辉和应雪海[37]的研究可知,在波动率模型中结合Markov状态转换机制确实能够改善波动率模型的预测效果,但国内外基于Markov状态转换机制的波动率模型的研究主要集中在GARCH族模型和HAR族模型.故本文借鉴Ma等[30]构建时变MRS-HAR族模型的思想,将基于显著跳跃方差(CJ)构建的时变Markov状态转换机制纳入到Realized GARCH族模型中,分别构建了时变MRS-Realized GARCH模型和时变MRSRealized EGARCH模型.为对比引入时变Markov状态转换机制与引入Markov状态转换机制的波动率模型的预测效果差异,本文还构建了MRS-Realized GARCH模型和MRS-Realized EGARCH模型.后文分别将这四种模型记为MRS-RealGARCH模型,MRS-RealEGARCH模型,时变MRS-RealGARCH模型和时变MRS-RealEGARCH模型.考虑收益率波动存在高波动状态和低波动状态,假设从交易日前一天的状态i到交易日当天的状态j的状态转移概率可以表示为

St为第t个交易日的状态变量,St=0表示高波动状态,St=1表示低波动状态,由此可得到状态转移概率矩阵

其中基于跳跃的时变状态转移概率为

其中CJt为第t个交易日的显著跳跃方差.由状态转移概率矩阵定义可知,(i,j=0,1).另外当λ0=λ1=0时,时变状态转移概率矩阵简化为状态转移概率矩阵.特别指出,由于本文仅考虑高波动和低波动这两种状态,则可参考Hamilton[38]的研究得到状态0的无条件概率
基于时变Markov状态转换机制,将Realized GARCH族模型的均值方程和波动方程分为两个状态,分别得到了时变MRS-RealGARCH模型和时变MRS-RealEGARCH模型3参考Ma等[30]构建MRS-HAR类模型的研究,本文的MRS-Realized GARCH族模型中波动方程的构建思想与其类似.

其中调整的已实现波动率测度为

由Pan等[36]的研究可知,第t个交易日的隐含波动率ht可由式(21)得到

其中Ωt为第t个交易日的信息域,P(St=i|Ωt−1)表示第t个交易日状态为i的先验概率.关于先验概率和参数估计的具体细节将会在后文叙述,在此不再赘述.
兰溪到衢州通常走的南岸,但南岸现在已基本落入鬼子之手,而兰溪的东南西三个方向也有日军重兵,唯一可能突围的就是往北,等突出包围圈,再折向西沿兰江而往上。
2.5 波动率模型的参数估计
为简便起见,本节仅给出了时变MRS-RealGARCH模型的参数估计过程,其余模型所对应的参数估计原理也可类似得到.
考虑资产波动率存在高波动状态(St=0)和低波动状态(St=1),则有

因此可根据全概率公式推导出zt的概率密度函数
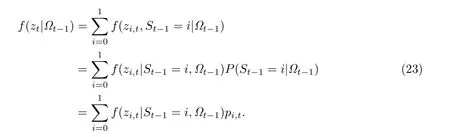
其中信息集Ωt包含了截止至第t个交易日的所有历史信息,pi,t为第t个交易日状态i的先验概率.根据全概率公式,pi,t具体为

由此便可得到时变MRS-RealGARCH模型的联合对数似然函数

根据条件设定参数初始值,逐步迭代计算联合对数似然函数,联合对数似然函数取最大值时所对应的参数便为各个参数的最优估计值.
2.6 波动率预测精度检验方法
采用滚动时间窗对样本外波动率进行预测和评估是衡量波动率模型预测效果好坏的常见方法,本节将详细介绍样本外滚动事件窗口技术和常见的波动率预测评估方法.将样本分为用于参数估计和模型拟合的样本内数据和用于模型评估的样本外数据,样本内和样本外数据分别包含H和M个交易日.通过舍弃最初的一个数据和在末端增加未来一个交易日的数据的滚动时间窗口技术,得到了长度为M的波动率预测序列.这保证了用于每一次滚动的样本内数据总量为固定值H,且预测区间不存在重叠现象.
由于损失函数无法在统计学意义上提供波动率模型预测精度的显著差异,本文采用Diebold和Mariano[40]提出的DM检验和Hansen等[41]提出的模型置信集(MCS)检验来评估波动率模型的预测能力的显著差异,这两种常见的评估方法在波动率预测精度评价的研究中得到了广泛应用.DM检验通过损失函数建立服从标准正态分布的DM检验统计量进行假设检验,根据检验统计量的p值是否落在拒绝域内来判断波动率模型的预测精度是否存在显著性差异.MCS检验是近年来比较流行的预测评估方法,与Hansen[39]提出的高级预测能力(SPA)检验相比,该方法不需要指定基准模型,且允许出现多个最佳模型的可能性.若某些模型MCS检验统计量的p值大于设定的临界值α,则这些模型可被称为幸存模型,其具有比剔除出最优模型集的模型更好的预测精度.若MCS检验的p值越大,则模型的预测效果越优.关于DM检验和MCS检验的具体介绍和原理可参见Diebold和Mariano[40]以及Hansen等[41].
§3 实证研究
3.1 数据说明
沪深300指数期货是中国金融期货交易所中极具代表性的期货合约,对金融产品的发展具有重要的推动作用.考虑到2015-2016年的牛熊周期复杂性,交易限制和2019年不稳定的贸易局势会对股指期货合约产生结构性影响,故选取2015年4月9日至2020年4月9日期间中国金融期货交易所的沪深300股指期货数据作为研究对象,共包含1221个交易日.结合Andersen和Bollerslev[42]和Liu等[43]的研究,已实现波动率测度RV对市场的微观噪声较为稳健,且在统计学意义上无法被多种波动率测度显著击败,选取5min间隔为采样频率,并根据式(2)计算RV.根据沪深300股指期货合约的交易规则,选取交易时间段收盘价数据,则每个交易日共包含48个收盘价数据.数据取自聚宽量化交易平台(JoinQuant),软件为R语言.另外,本文选取前721个样本作为样本内数据,后500个交易日数据作为样本外数据以用于模型的预测能力评估.
3.2 描述性统计分析
图1分别给出了沪深300股指期货数据的收盘价,对数收益率rt,已实现波动率测度RVt,调整的已实现波动率测度Ct和显著的跳跃方差CJt的折线图.表1给出了对数收益率rt,已实现波动率测度RVt,调整的已实现波动率测度Ct和显著跳跃方差CJt的描述性统计量.由表1可知,日对数收益率存在左偏和厚尾的现象,而已实现波动率测度RVt和它的两种成分Ct和CJt均存在右偏和厚尾现象,且波动程度较为剧烈.在5%的水平下,LM(10)和LB(10)检验统计量均显示金融时间序列存在10阶自相关性,且基于AIC准则的ADF检验结果显示金融时间序列不存在单位根,这表明利用基于高频数据的波动率模型进行建模是合理的.另外,JB统计量结果显示,在5%的水平下,序列并不服从正态分布的假设.
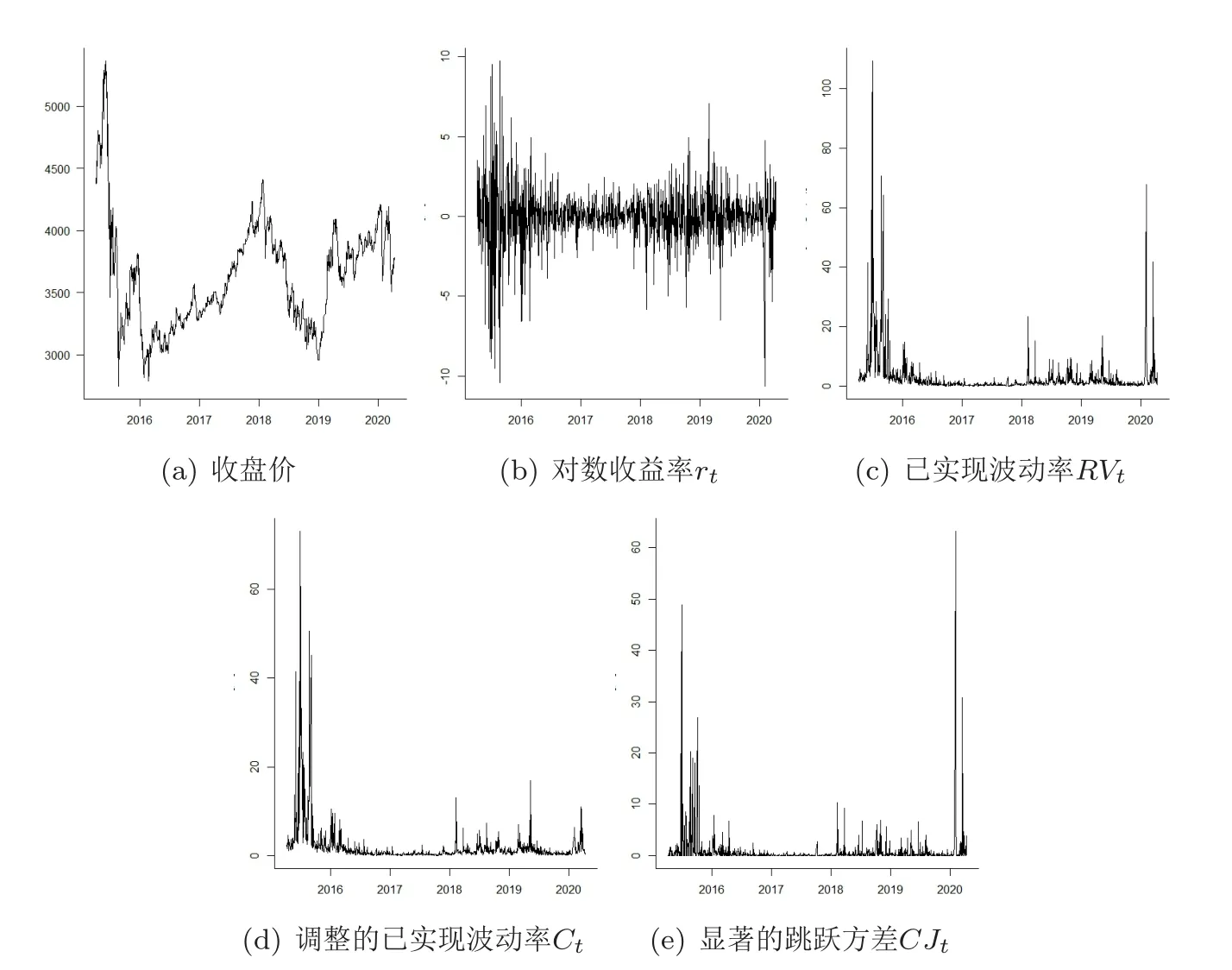
图1 描述性统计图

表1 描述性统计量
3.3 参数估计
表2给出了Realized GARCH模型和Realized EGARCH模型在残差服从标准正态分布下的参数估计结果.其中l(r)为半似然函数,l(x,r)为对数似然函数值,半似然函数值和似然函数值分别反映了波动率模型中收益率拟合情况和整体的拟合情况.半似然函数值越大,则收益率拟合情况越好;似然函数值越大,则波动率模型的整体拟合情况越好.由表2可知,Realized GARCH模型和Realized EGARCH模型的大部分参数在1%的水平下均显示显著.由Realized GARCH模型波动方程的参数估计结果可知,截距项系数α0显著为正,一阶滞后条件波动率系数α1与一阶滞后已实现波动率系数β1之和接近于1,且后者对隐含波动率的贡献更大,即前一期的已实现波动率对当期条件方差的正向冲击高于前一期条件方差.由Realized EGARCH模型波动方程的系数估计结果可知,截距项系数显著为负,一阶滞后条件波动率系数β1接近于1,表明金融资产的波动率具有较高的持续性.杠杆参数d显著为负,表明杠杆效应对未来一天的沪深300股指期货波动率存在显著的负向冲击.由测量方程的参数估计结果可知,两个模型的参数估计不存在较大差异,即测量方程中的噪声扰动项对于波动率模型的结构差异较为稳健.φ ≈1进一步表明隐含波动率与已实现波动率测度具有很强的相关性.另外,Realized EGARCH模型的半似然函数和似然函数值普遍高于Realized GARCH 模型,则前者的拟合效果优于后者,即在波动方程中引入杠杆效应确实能够提高金融资产收益率的拟合情况,这与Hansen和Huang[34]的研究结果一致.

表2 Realized GARCH族模型参数估计
表3给出了MRS-RealGARCH模型和MRS-RealEGARCH模型的参数估计结果.考虑金融资产波动率存在高波动率和低波动率两种状态,本文计算了样本内拟合过程中残差扰动项的方差来区分两种波动状态,分别将高波动率和低波动率记为状态0和状态1.两个模型状态0 的残差扰动项的方差分别为1.337,1.666;状态1的残差扰动项的方差分别为0.771,1.087.另外,大部分参数在1%的水平下显著.MRS-RealGARCH模型波动方程的参数估计结果显示,跳跃测度系数βi,2在不同波动状态下对波动率产生不同方向的冲击,其在低波动状态并不显著,对条件波动率的冲击也弱于高波动状态.特别地,在不同的波动状态下,一阶滞后已实现波动率测度对期货资产波动率的影响也存在较大差异.MRS-RealEGARCH模型波动方程的参数估计显示,杠杆系数d和噪声扰动项系数γ一负一正,且在1%的水平下显著,两者在高波动状态对波动率的影响明显高于低波动状态.另外,通过计算可得到MRS-RealGARCH模型状态之间转移的概率分别为p0,0=0.736,p0,1=0.264,p1,0=0.792,p1,1=0.208;MRS-RealEGARCH模型状态之间转移的概率分别为p0,0=0.630,p0,1=0.270,p1,0=0.716,p1,1=0.284.由两个模型的p0,0可知,若当前交易日处于高波动状态,则未来一期处于高波动状态的概率较高,这与图1(b)中观察到的波动集聚现象一致.根据Hamilton[38]的研究计算两个模型两个状态的先验概率,MRS-RealGARCH模型状态0的先验概率为0.250,而MRS-RealEGARCH模型状态0的先验概率为0.341.从收益率和收盘价的时间序列图可以看出处于低波动状态的概率要低于处于高波动状态的概率,且从前一天波动转换成低波动状态的概率也低于高波动状态,这与先验概率相吻合.另外,由半似然函数和似然函数可知,引入Markov状态转换概率机制的Realized GARCH族模型的拟合结果也有了显著提升.

表3 MRS-RealGARCH族模型参数估计
表4为时变MRS-RealGARCH族模型的参数估计结果.时变MRS-RealGARCH模型和时变MRS-RealEGARCH模型残差扰动项在高波动状态下的方差分别为1.342和1.294,在低波动状态下的方差分别为0.599和0.620.观察时变MRS-RealGARCH模型波动方程的参数估计可知,一阶滞后隐含波动率和已实现测度在高波动状态对波动率的冲击高于低波动状态,而跳跃测度对波动率的影响只有在低波动状态才显著为正,其对未来一天波动率的冲击高于高波动状态.在时变MRS-RealEGARCH模型中,所有参数在5%的水平下均显示显著,一阶滞后已实现波动率在高波动状态与未来一期的波动呈现更高的相关性.另外,前一天的负收益率在低波动状态会对未来一天波动造成更为显著的负向影响,而前一天的噪声扰动项在两种状态下均对当期波动产生显著的正向影响,且在高波动状态的影响更大.两个模型的测量方程参数的估计结果不存在显著差别,由状态转移概率矩阵的四个估计参数可知,显著跳跃方差CJt在两种状态下会对状态转移概率造成相反方向的显著影响.最后,半似然函数和似然函数值显示,引入时变Markov状态转换机制确实能够提高模型的拟合能力.

表4 时变MRS-RealGARCH族模型参数估计
3.4 样本外波动率预测效果评价
将样本量分为两个部分: 用于波动率模型拟合的样本内数据和用于评估滚动预测效果的样本外数据,数据长度分别为721和500.利用一步滚动窗口预测技术以保证用于模型拟合的样本长度不变,滚动500次便可得到Realized GARCH模型,Realized EGARCH模型,MRS-RealGARCH模型,MRS-RealEGARCH模型,时变MRS-RealGARCH模型和时变MRSRealE GARCH模型等6个波动率模型的波动率预测序列,每个序列的长度均为500.为比较引入Markov状态转换机制和时变Markov状态转换机制对模型预测精度的改进效果,本文将Realized GARCH模型,MRS-RealGARCH模型,时变MRS-RealGARCH模型归为一组,将Realized EGARCH模型,MRS-RealEGARCH模型,时变MRS-RealEGARCH模型归为另一组,通过DM检验来比较模型改进前后的波动率预测效果.
表5和表6分别给出了两组模型的DM检验结果,前3行为模型的损失函数值,Ratio1和Ratio2分别表示包含MRS和时变MRS机制的波动率模型的损失函数与原模型所对应的损失函数的差值比例.以Ratio1为例,其计算如下式所示.
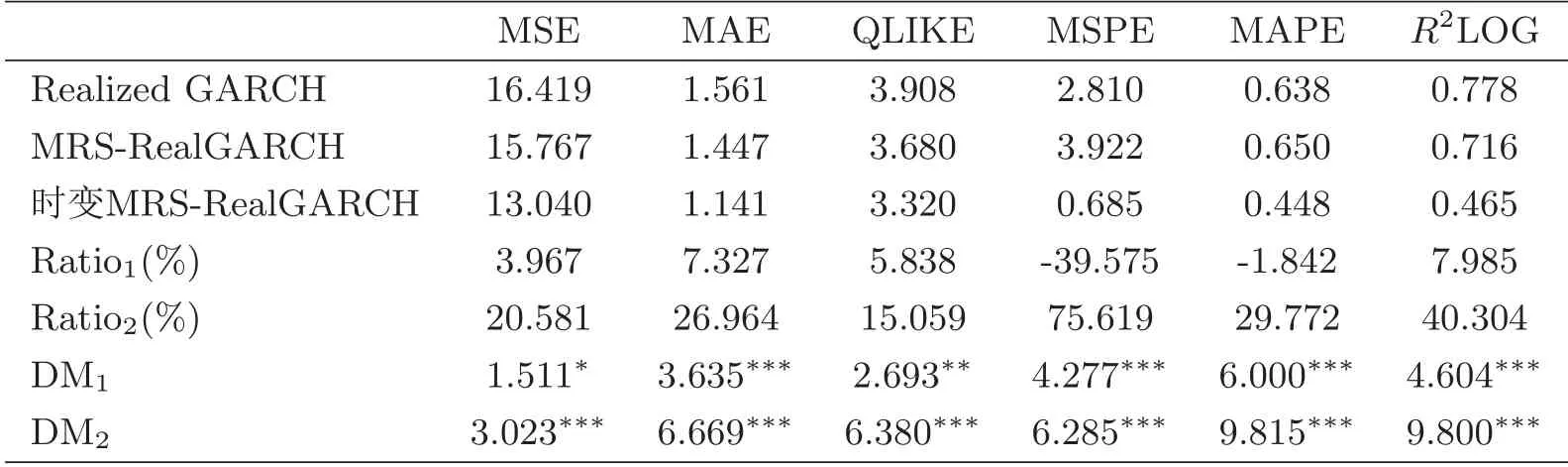
表5 Reallized GARCH模型及其改进模型的一步滚动预测结果

表6 Realized EGARCH模型及其改进模型的一步滚动预测结果

Lossi,bench为对照模型(Realized GARCH模型或Realized EGARCH模型)的第i个损失函数值,Lossi,model为改进模型的第i个损失函数值.若比例为正,则改进后的模型预测精度优于原模型;反之,改进后的模型预测精度劣于原模型.因此,若比例越大,则模型改进后的效果越好.DM1和DM2分别为通过包含MRS和时变MRS机制的模型一步滚动预测得到的DM 检验统计量.该统计量服从标准正态分布,若p值小于给定的水平,则DM检验拒绝原假设,表明改进后的模型具有显著的改进效果.特别指出,在拒绝原假设的情况下,DM检验统计量越大,模型的波动率预测精度更高.
由表5和表6,除了MRS-RealGARCH模型和MRS-RealEGARCH模型在MSPE和MAPE两个损失函数指标下的损失函数比原模型高以外,改进模型的损失函数均比原模型小.另外,包含时变MRS机制的波动率模型所对应的DM检验统计量在数值上显著高于包含MRS机制的波动率模型.值得注意的是,基于部分损失函数值得到的结论与DM检验结果并不一致(如MRSRealGARCH模型在MSPE和MAPE指标下的损失函数值和DM检验),这可能是因为某些特殊观察值对损失函数造成了较大的影响,因此采用DM检验等统计检验方法比较波动率模型预测精度在统计学意义上的显著差异显得十分必要.
另外,本文在接下来的MCS检验过程中将以上6类波动率模型归为一组以研究加入杠杆效应是否会对波动率模型的预测能力具有改进效果.表7给出了基于两种统计量TSQ和TR在5%的水平下的MCS检验p值.由表7可以看出,无论是Realized GARCH模型还是Realized EGARCH模型,它们的拓展模型在6大损失函数指标和两种检验统计量下的p值均高于原模型,且包含时变MRS机制的RealGARCH族模型相比于MRS-RealGARCH族模型具有更高的检验p值,即包含时变MRS机制的RealGARCH族模型具有最佳的波动预测表现.另外,Realized EGARCH模型和MRS-RealEGARCH模型在6大损失函数指标和两种检验统计量下的12次MCS检验p值在多数情况下高于Realized GARCH模型和MRS-RealGARCH模型,且时变MRS-RealEGARCH模型有10次被MCS检验认为是表现最好的模型,这意味着考虑杠杆效应的波动率模型具有更好的波动预测精度.

表7 MCS检验
§4 时变MRS-RealGARCH族模型的稳健性检验
为进一步说明引入时变Markov状态转换机制对Realized GARCH族模型的波动率预测能力具有显著的改善效果,本章分别从不同的波动率预测精度评估方法,误差分布假设,采样区间,滚动窗口以及跳跃测度等方面验证时变MRS-RealGARCH族模型的优越性.
4.1 不同的预测精度评估方法
样本外R2统计量()是金融市场波动率预测研究的常用方法,Campbell和Thompson[44],Rapach等[45]和Wang等[46]将其应用于各类金融波动率模型以比较预测精度.若为正,则改进模型的预测精度优于对照模型.本文也采用这一种流行的评估方法来评估波动率模型的预测精度差异.关于和其检验统计量ft的具体介绍见文[46].以Realized GARCH模型为对照模型,其余模型为改进模型,通过计算和检验统计量ft便可得到基于一步滚动预测的样本外检验结果(见表8).由表8可知,只有时变MRS-RealGARCH模型和时变MRSRealEGARCH模型的在1%的水平下显著,且其值远大于其他模型,这进一步说明了在高频波动率模型中引入时变MRS机制的优越性.

表8 样本外R2oos
4.2 不同的误差分布假设
在上章的实证研究中,仅仅假设波动方程中的误差分布服从标准正态分布.然而,根据表1的描述性统计分析可知,收益率序列存在显著的尖峰厚尾性,即其不服从正态分布的假设.因此,考虑到t分布和GED分布作为常见的厚尾分布在金融数据波动率模型研究中得到了广泛应用,本节将高频波动率模型的残差分布分别拓展到t分布和GED分布,期望以此来研究时变MRS机制对模型的改进效果对于误差分布为厚尾分布的假设是否依旧稳健.受篇幅所限,本文并未展示时变MRS-RealGARCH族模型在误差分布分别服从学生t分布和GED分布情况下的联合对数似然函数.
同样将数据分为长度为721的样本内数据和长度为500的样本外数据,通过一步滚动窗口预测技术得到了各模型的波动预测序列.表9给出了误差分布服从学生t分布和GED分布假设下的各模型MCS检验结果.观察表9可知,在5%的水平,任意损失函数和MCS检验统计量指标下,MCS检验均将Realized GARCH模型和Realized EGARCH模型剔除出最优模型集.包含MRS机制和时变MRS机制的Realized GARCH族模型的p值在大多数情况下高于原模型.在12次的MCS检验过程中,MCS检验均认为时变MRS-RealGARCH族模型是预测精度最高的波动率模型,这表明基于跳跃测度的Markov状态转换机制对波动率模型的改进效果更为显著.另外,在两种厚尾分布的假设下,MCS检验认为时变MRS-RealGARCH模型为最优模型的次数高于时变MRS-RealEGARCH模型.

表9 基于厚尾分布的MCS检验结果
4.3 不同的采样区间
为验证本文所构建的模型的波动率预测效果对于不同的采样区间依旧稳健,选取沪深300股指期货的2013年4月10日至2018年4月11日共1221个交易日的高频数据和低频数据.同样将前721个数据归为样本内数据,将后500个数据归为样本外数据,通过一步滚动窗口预测技术便可得到各模型的波动率预测序列.表10给出了基于不同采样区间的模型样本外波动率预测的MCS检验结果,由各模型在六种损失函数和两类检验统计量下的MCS检验p值可知,在5%的水平下,Realized GARCH模型,Realized GARCH模型,MRS-RealGARCH模型和MRS-RealEGARCH模型等4个波动率模型在任意损失函数(除MSE外)和检验统计量下的MCS检验p值均小于0.05,即在10次检验过程中,MCS检验均将它们剔除出最优模型集.而在12次MCS检验中,MCS检验共有8次认为时变MRS-RealEGARCH模型是表现最佳的波动率模型,有4次认为时变MRS-RealGARCH模型为最优模型.

表10 基于不同采样区间的MCS检验结果
4.4 不同的滚动窗口
上文的实证分析选择长度为721的一步滚动窗口来预测波动率得到了长度为500的预测序列,本节为验证基于时变Markov状态转换机制对Realized GARCH族模型的改进效果是否对不同的预测窗口长度稳健,分别选取长度为821,921和1021的一步滚动窗口来预测波动率,得到了长度为400,300和200的预测序列.
表11给出了预测序列长度为200,300和400的波动率序列的MCS检验结果.MCS检验结果显示,不同滚动预测窗口的MCS检验存在较为显著的差异.在任意一步滚动预测窗口(200,300和400)的设定下,对于任意的损失函数和检验统计量,MCS检验在12次检验中均认为时变MRS-RealGARCH族模型是最佳的波动率模型,即在高频波动率模型中引入基于跳跃测度的Markov状态转换机制来刻画金融资产的非线性结构能够提升模型的预测效果.另外,MCS检验判定时变MRS-RealEGARCH模型为最优模型的次数多于时变MRS-RealGARCH模型,这意味着沪深300期货市场存在显著的杠杆效应,在波动率建模中考虑这一金融特征能够提高模型的波动预测能力.

表11 基于不同滚动窗口的MCS检验结果
4.5 不同的跳跃测度
考虑到双幂次变差跳跃Jt,符号跳跃SJVt,符号正向跳跃和符号负向跳跃等常见的跳跃测度已被广泛应用于金融市场高频波动率模型的研究[30,37,48-49],本文期望通过这几种常见的跳跃测度来构建时变MRS机制,并通过一步滚动窗口预测技术和MCS检验来比较模型预测精度.

表12 基于不同跳跃测度的MCS检验结果
§5 结论
基于跳跃测度和Markov状态转换视角,考虑到金融资产波动率存在结构突变和非线性结构等特征,文章将时变Markov状态转换机制与Realized GARCH族模型相结合,构建了时变MRS-RealGARCH族模型,推导其参数估计方法,应用一系列预测检验方法评估新模型的波动预测效果,并基于不同方面对该模型进行稳健性检验.
本文的主要结论有: 第一,样本内拟合结果表明期货市场存在高波动和低波动状态,在不同状态下跳跃测度对未来一期的波动具有不同的影响效果,其中负收益率在高波动状态会对未来一期的波动造成更为显著的影响.第二,DM检验和MCS检验均显示,引入非线性结构的时变MRS机制能够提高波动率的预测效果.在任意损失函数指标下,时变MRS-RealGARCH族模型均为最佳的波动率模型,且考虑杠杆效应的时变MRS-RealEGARC模型的波动预测精度高于时变MRS-RealGARCH模型.第三,稳健性检验结果均显示,时变MRS-RealGARCH族模型均具有更优的预测能力.
此外,本文揭示了我国沪深300期货的波动规律,对于研究我国沪深300期货市场的风险度量和投资组合等问题均具有重要的理论和实际价值,为投资者和管理者认识期货市场波动规律提供了借鉴意义.
