Buck开关电源的极限学习机滑模控制器设计

陈 龙，储梦贤

（杭州电子科技大学电子信息学院，浙江杭州 310018）

0 引言

线性电源需要体积庞大的散热片，而开关电源具有小型、轻量、高效率等特点，成为电源的主流选择［1-3］。Buck开关电源采用控制开关管达到降压的目的，这种开关控制使得各种控制算法非常适合应用于此，但设计其控制策略时，电磁干扰、寄生电阻、元件内阻的功耗问题均会对其性能产生一定影响［4］。

近年来业内涌现了神经网络控制、模糊控制、自适应控制、滑模控制（Sliding Mode Control，SMC）等控制算法［5-6］，其中滑模变结构控制不要求高精度数学模型，对外部扰动和系统参数摄动具有强鲁棒性［7］，因此非常适用于Buck 开关电源的控制。然而经典SMC 算法的响应速度仍然需要得到进一步提升，为此文献［8］提出一种变指数多幂次趋近律，以提高永磁同步电机系统的收敛速度，但未解决时变干扰对控制器性能的限制性，在外部环境发生剧烈变化时，系统品质明显变差。为解决系统干扰变化的问题，文献［9］使用扩张观测器追踪系统的扰动，并设计了积分时变滑模面以提高系统鲁棒性。该方案虽然改善了系统动态性能，但并未将趋近律考虑到控制器的设计中，会进一步缩短趋近运动的时间；文献［10］提出的径向基神经网络对系统的不确定性和电机力矩扰动进行实时估计，但径向基神经网络结构复杂且对参数具有依赖性，从而导致控制器的输出品质存在波动的缺点。

极限学习机（Extreme Learning Machine，ELM）是基于前馈型神经网络的算法，与传统神经网络学习方法相比，其输入层和隐藏层的连接权重可以随机设定且不用再次调整，隐藏层节点的权重则是通过方程组求解的方式一次确定，大幅度提高了ELM 的训练速度［11-12］。本文针对Buck 开关电源，提出将ELM 设计干扰观测器用于快速逼近系统的集总干扰，训练过程只涉及广义逆矩阵的求解，结构简单。结合终端滑模函数、线性滑模函数、积分滑模函数的优点，本文设计了积分终端滑模函数，并使用指数趋近率，综合考量趋近运动与滑模运动的效率，使用李雅普诺夫函数证明系统的稳定性；然后在PSIM 软件中建立了Buck 开关电源仿模型，与传统滑模控制算法进行比较，结果表明所设计的控制器不仅在启动响应速度方面有明显提升，在发生外部干扰时亦表现出更强的鲁棒性，抖振的超调量更小。

1 Buck开关电源系统模型建立

图1 为Buck 开关电源的拓扑结构，开关管导通St时，储能电感L被充磁，同时给电容C充电，给负载R提供能量。开关管St关断时，储能电感L通过续流二极管放电，输出电压靠输出滤波电容C放电以及减小的电感电流维持［13-14］。在输入电压Vin恒定的情况下，可以通过脉冲宽度调制控制开关管St 的导通时间和截止时间改变输出电压Vo。导通时间Ton和开关周期T的比值为占空比D，且D∈（0，1），因此

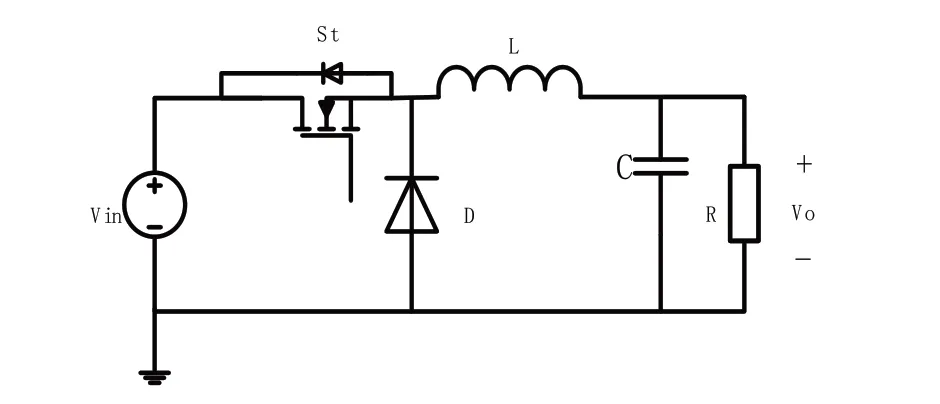
Fig.1 Buck switching power supply topology图1 Buck开关电源拓扑结构

经过上述分析，得到系统的二阶数学模型为：

式中，d0为外部时变干扰；u为开关控制函数，其值由滑模控制器的输出经过脉冲宽度调制电路得到。为达到精确的控制效果，采用名义模型对系统建模［15］，式（1）可表示为：

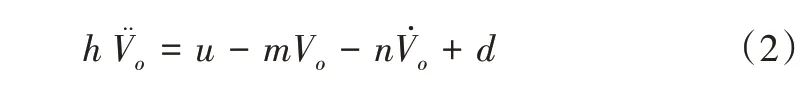
式中，h=h0+h1，m=m0+m1，n=n0+n1，其中h0、m0、n0表示系统参数的标准值，h1、m1、n1为系统参数中不能精确获得的值表示系统的集总干扰。

2 控制器设计

2.1 积分终端滑模控制器设计

Buck 开关电源的理想输出电压Vref为1 个常数，系统的跟踪电压误差e=Vo-Vref，则由式（3）得到：

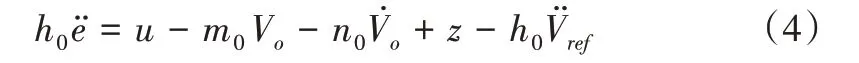
在普通的终端滑模函数中引入积分项和线性项构造积分终端滑模函数s，表示为：

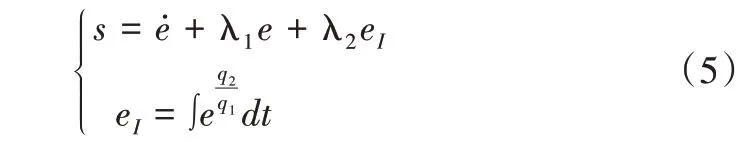
式中，λ1和λ2为大于零的常数，q1和q2为正奇数，且q1/q2>1。

计算滑模函数s的一阶导数，表示为：

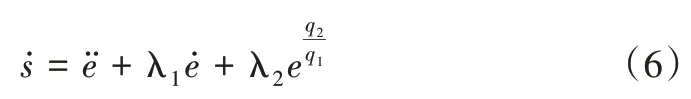
在理想模型中，忽略不确定因素对系统的影响，可得到系统的等效控制输入ueq为：

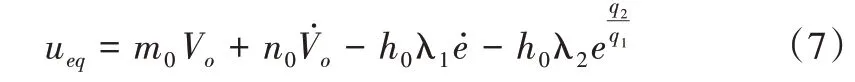
为了补偿系统的不确定性和干扰，引入ELM 对z进行拟合作为干扰补偿输入项uELM，表示为：

最后滑模趋近率选择：

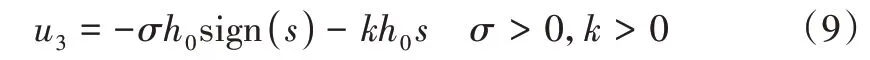
综合式（7）-（9）得到最终的控制器输入为：

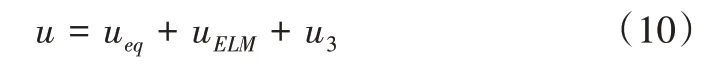
2.2 ELM观测器设计

ELM 有比传统神经网络模型更快的学习速度和更高的效率［16］。系统中对误差的补偿项恰恰需要快速而准确的估计，因此ELM 很适用于Buck 开关电源的误差跟踪。图2为含单隐层的三层前馈ELM 的网络结构。

三层前馈ELM 的网络结构主要包括输入层、隐藏层和输出层。将输入层的数据x=[x1，x2，…，xn]T和输入权重W=[w1，w2，…，wL]T相乘，再加上相应的偏置b=[b1，b2，…，bL]T作为隐藏层激活函数的输入，其中W和b由随机概率得到［17］。

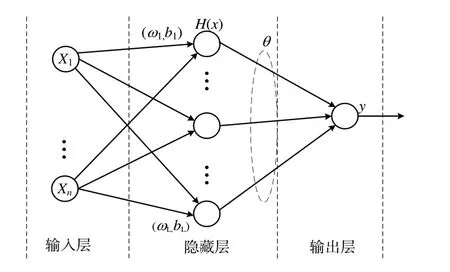
Fig.2 Three layer feedforward ELM network structure图2 三层前馈ELM网络结构

隐藏层的输入WTx+b经激活函数G(·)的作用后得到隐藏层的输出H，其中G(·)为激活函数，选用非线性的函数Sigmoid，满足ELM 通用逼近能力定理［18］，表示为：

隐藏层的输出乘以隐藏层到输出层之间的权重θ=[θ1，θ2，…，θL]T，得到EL M的输出，表示为：

为得到输出权重θ的最优解，采用ELM 的输出和训练样本集输出的平方差最小值作为目标函数，得到目标函数最小的输出权重θ值即为最优解θ*，表示为：

式中，H为N 组训练数据的隐藏层输出矩阵，Y为N 组训练样本的标签，分别表示为：

最后得到最优解θ*为：

式中，H+为矩阵H的广义逆矩阵。

通过ELM 得到的系统误差估计值为：

实际干扰z为：

式中，δ表示ELM 的估计误差，其在量值上相对于拟合量是一个比较小的正数。

2.3 稳定性分析

李亚普诺夫方程V表示为：

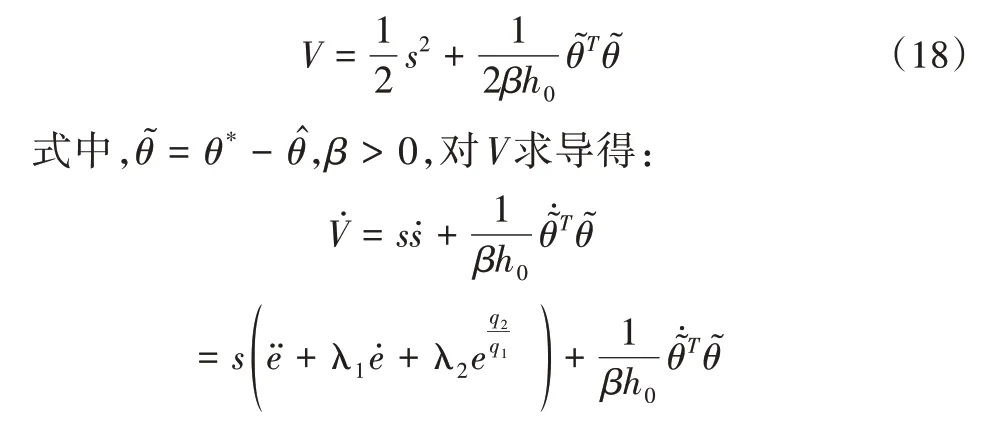
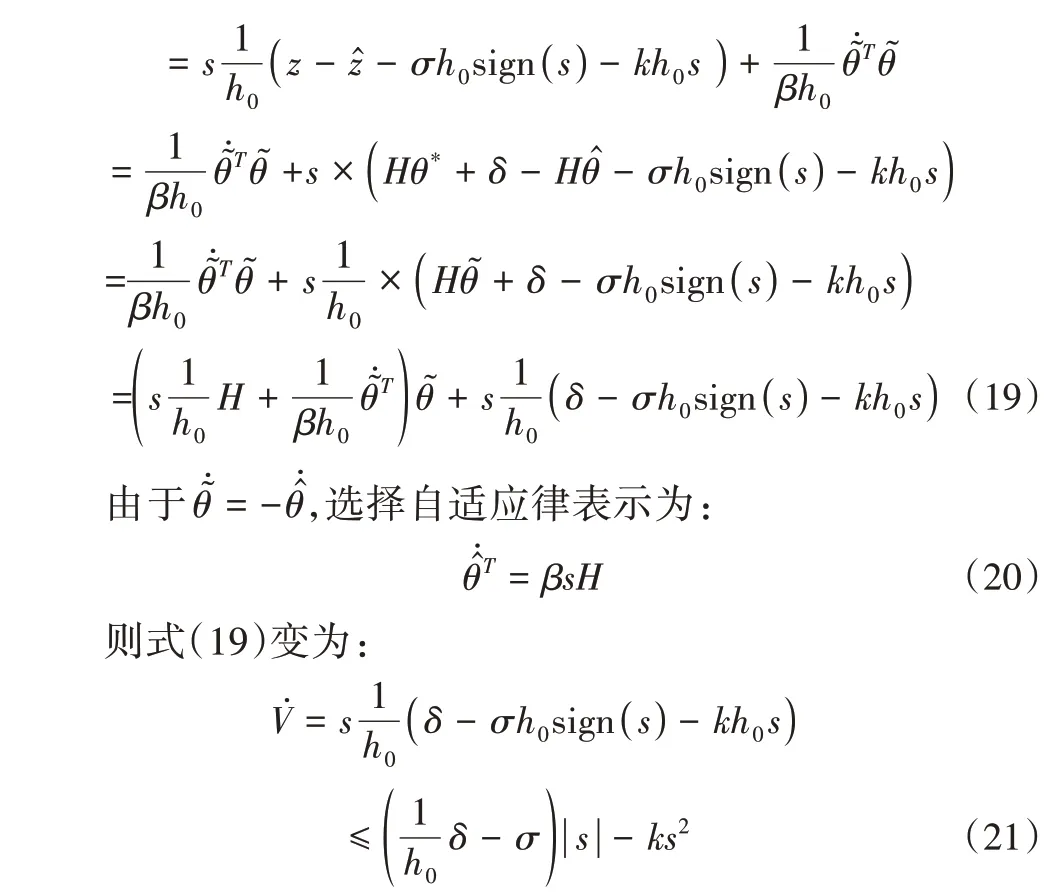
3 系统仿真与分析

设计完成滑模控制器后在PSIM 软件中对系统进行建模，其中电流内环采用PID 控制，外电压环分别使用普通滑模控制器（SMC）与本文设计的ELM 积分终端滑模控制器（ELM Integral Terminal Sliding Mode Controller，ELMITSMC）进行仿真比较，Buck 开关电源仿真模型见图3（彩图扫OSID 码可见，下同）。

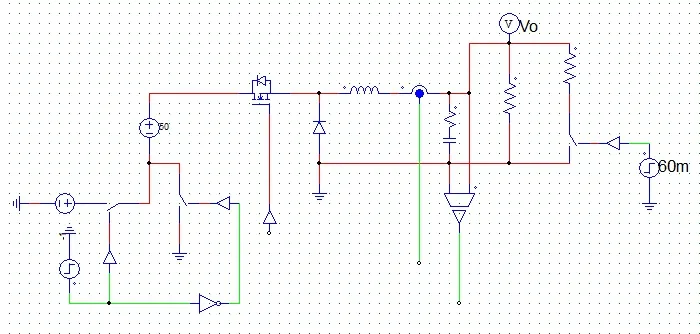
Fig.3 Buck switching power PSIM simulation model图3 Buck开关电源PSIM仿真模型

仿真系统中Buck 开关电源各项参数设置如表1所示。

Table 1 Buck switching power supply parameters表1 Buck开关电源参数

本文设计的控制器主要分为两个部分：一部分由等效控制ueq和趋近率控制器u3组成；另一部分则由ELM 对系统总干扰的观测值uELM构成。电压环的控制经由数学变化得到内环电流的参考值，与电感电流经过PI 控制，由脉冲宽度调制技术产生开关管St的方波。系统总体设计框图如图4所示。

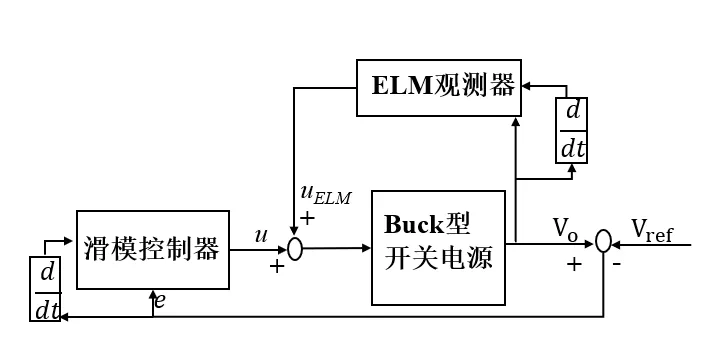
Fig.4 Block diagram of the overall system design图4 系统总体设计框图

选取合适的控制器参数，比较SMC 与本文设计的ELMITSMC 算法的性能。图5 为两种控制器输出电压的启动响应。仿真结果显示，SMC 算法在启动后18 ms 恢复到参考电压，而ELMITSMC 算法可在9.6 ms内恢复。

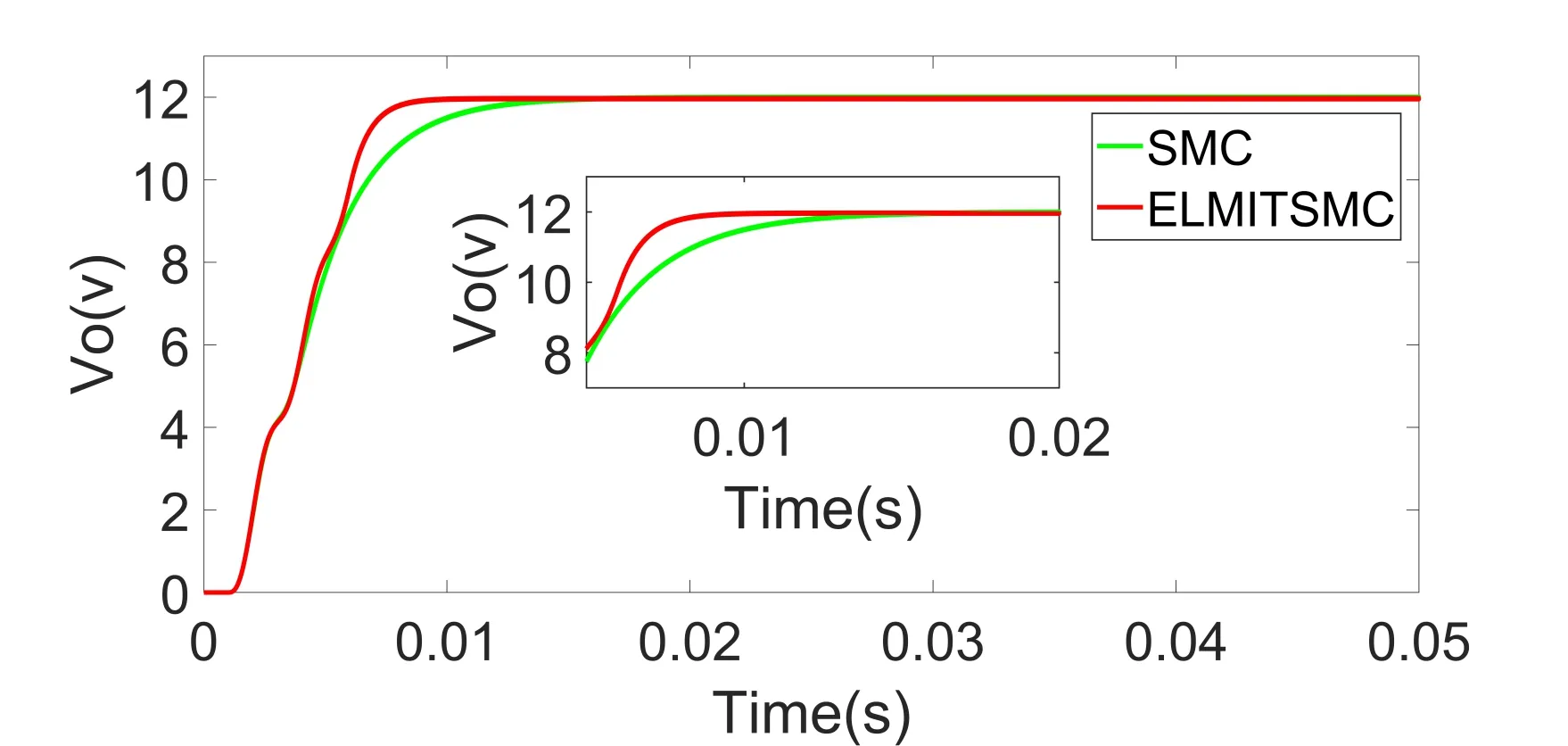
Fig.5 Two kinds of controller output voltage start-up response图5 两种控制器输出电压启动响应

为验证所设计的ELM 观测器估计系统干扰的能力，在系统处于稳定的情况下，t=0.06 s 时将输入电压减小0.5V以模拟系统的输入电压干扰，结果如图6 所示。两种控制算法在系统发生干扰时输出电压均会减小，ELMITSMC 算法在2ms 内迅速收敛，而SMC 算法则长达12.3ms，且ELMITSMC 算法受到干扰时电压下降幅度也更小。

Fig.6 Two controller output voltage interference response图6 两种控制器输出电压干扰响应

图7 为系统稳定状态下，t=0.06 s 时将负载电阻减小为12Ω 的输出电压响应。可以看出，当负载电阻减小时，系统输出电压先减小，后经过一段时间恢复到参考电压。ELMITSMC 算法经过2ms 恢复，比SMC 算法快了18ms。SMC 算法控制下最大抖动幅度为0.99V，扰动量为8.25%；ELMITSMC 算法在发生负载切换时最大的抖动幅度为0.27V，扰动量为2.25%，受到干扰后抖动幅度明显减小，并且恢复极快。

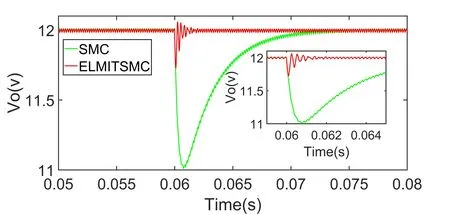
Fig.7 Load switching interference response of two controllers图7 两种控制器负载切换干扰响应

4 结语

本文针对Buck 开关电源系统，关注于外界非线性时变干扰对控制器品质的影响，设计了一款带有ELM 干扰观测的积分终端滑模控制器。该滑模控制器能有效消除系统稳态误差，自动调整平衡状态吸引因子，在有限时间内使Buck 开关电源系统收敛，同时将ELM 神经网络的预估结果快速准确地前馈补偿到控制器模型中，以减弱控制输出的高频抖动幅度，与传统SMC 的仿真对比结果体现了本方案输出电压的快速跟踪性和平滑性。基于该控制器设计的Buck 开关电源对于设计高效率、高稳定的供电设备具有一定的参考价值。后续可从对趋近律的改良以及ELM 神经网络结构的优化等方向出发，探索开发更高品质的控制器结构。