基于SARIMA-SVM 组合模型的地铁客流量预测研究

邵必林，饶 媛，何 欣

（西安建筑科技大学管理学院，陕西西安 710055）

0 引言

中国作为基础建设工程大国，城市轨道交通发展十分迅速，处于世界轨道交通发展前列。截至2020 年，中国地铁运营线路6 280.8km，中心城市轨道交通客运量占公共交通客运总量出行率的38.7%，相较于2019 年提升4.1%。从交通运输部的客流月报中可知，人们出行选择公交的占比降低，地铁客流运输量占比逐渐增加。

地铁相较于其他交通方式，具有速度快、客运乘载量大、准点率高的突出优势。随着地铁成为日常出行的主要交通工具，人们对地铁建设、运营及规划提出更高的要求。在地铁建设和运营过程中，预测客流量是一个不可或缺的工作，该结果的可靠性对地铁的建设投资、运营效率及经济效益起到至关重要的作用［1-2］。

现有客流量预测模型主要分为以时间序列模型为主的参数模型、以机器学习为主的非参数模型及多方法混合的组合预测模型。其中，时间序列预测模型包括自回归模型（Auto-Regressive，AR）、移动平均模型（Moving Average，MA）、差分自回归移动平均模型（Auto-Regressive Integrated Moving Average model，ARIMA）［3］及季节性差分自回归移动平均模型（Seasonal Autoregressive Integrated Moving Average，SARIMA）［4］。赵鹏等［5］运用ARIMA 模型预测北京地铁路网中的典型车站的客流量，验证差分自回归移动平均模型的有效性。蔡昌俊等［6］以广州地铁各车站进出站客流数据为例，证实ARIMA 模型的平均绝对百分误差可保持在5%以内。李洁等［7］将预测步长作为短期客流预测的影响因素，以广珠城际铁路为例证实SARIMA 模型可运用于多步预测，相较于其他预测模型具有一定的优势。孙湘海等［8］研究发现考虑交通流数据中日及周周期性的SARIMA 模型的预测效果最好。

此外，由卡尔曼滤波理论（Kalman Filtering Theory）衍生的卡尔曼滤波模型也属于参数预测模型。朱中等［9］构建长春市重要交通通道的交通流量预测模型，模型结构简单，仅利用历史数据进行预测。但该模型需要设置诸多假设、映射关系等条件，在实际应用过程中的适应性较差。

非参数模型包括支持向量机（Support Vector Machines，SVM）模型、神经网络模型等。其中，支持向量机模型属于传统机器学习模型，能够拟合观测数据中的非线性规律，该模型利用数据规律对未来数据或无法观测的数据进行预测。付晓刚等［10］运用SVM 预测模型对春运期间的客流进行预测，验证SVM 模型预测客流的可行性。杨军［11］使用SVM 模型预测北京轨道交通客流，实验结果表明SVM 模型在不同时间粒度情况下，均具有较高的预测精度。神经网络模型模型包括BP 神经网络（Back Propagation Neural Network，BPNN）、卷积神经网络（Convolutional Neural Networks，CNN）、长短期记忆网络（Long Short-Term Memory Networks，LSTM）等［12-13］。杨新苗等［14］将自适应性较强的模糊神经网络（Fuzzy Neural Networks，FNN）引入公交线路客流的预测研究中，实验结果表明该模型的预测精度优于常规AR、ARMA 模型。Wang 等［15］分析BP 神经网络与铁路客流时间序列的适用性，以此指导列车运输组织方案。Gallo 等［16］使用人工神经网络（Artificial Neural Network，ANN）预测地铁客流，并使用仿真数据及那不勒斯地铁一号线的客流进行实例测试。实验结果表明，神经网络模型相较于以往模型具有更高的预测精度，但神经网络模型通常需要计算大量数据，所需时间过长，易受到数据规模、网络深度及算法复杂度的影响。

为此，目前通常结合两个及以上模型以精确、有效地预测地铁客流量［17］。徐熠明等［18］结合指数平滑法与改进马尔可夫模型预测上海市轨道交通节假日的客流量。滕靖等［19］等使用粒子群优化（Particle Swarm Optimization，PSO）算法对传统的LSTM 模型进行优化，同时考虑天气、日期等因素对模型预测精度造成的影响，证明混合模型的预测效果优于单一模型。翁钢民等［20］使用PSO 算法选取支持向量回归机（Support Vector Regression，SVR）的回归参数，模型预测的均方差相较于SVR 提高67.3%。屈晓宜［21］结合神经网络与集成经验模态分解（Ensemble Empirical Mode Decomposition，EEMD），构建城市轨道交通客流预测的统计分析模型，缩短了神经网络模型的预测时间，并将预测精度提高到90%以上。刘维源等［22］运用ARIMA模型拟合短时客流量均值，引入广义自回归条件异方差模型（Generalized Autoregressive Conditionally Heteroskedastic Models，GARCH）对客流方差进行拟合，相较于单一模型预测精度提高30%。综上所述，组合模型既能充分发挥各预测模型的优点，又能提高预测精度，缩短预测时间。

然而，以上的方法均未考虑不同日期类型的地铁客流规律。为了解决该问题，本文结合SARIMA 与SVM 模型预测不同日期类型的地铁日客流量。其中，SARIMA 对客流数据线性部分具有良好的分析能力［23-24］；支持向量机（SVM）能很好的适应非线性映射，防止模型发生过拟合，泛化错误率低，结果易解释［25-26］。

1 相关理论

1.1 SARIMA模型

自回归模型（AR）和移动平均模型（MA）共同构成常用的时间序列预测模型——ARIMA 模型。具体的，AR 模型基于变量历史时间数据对自身进行预测，描述的是当前值与历史值间的关系；MA 模型通过累加AR 模型中的误差项消除预测中发生的随机波动。

由于AR 模型和MA 模型预测时，要求时间序列必须属于平稳阶段，然而在实际生活中获取的时间序列通常为非平稳数据，无法适用于以上两种模型。

由于地铁客流数据是典型的时间序列，属于季节性、非平稳的时间序列。为此，本文先对非平稳数据进行差分，待形成平稳时间序列后利用ARIMA 模型进行预测。

季节性时间序列指该序列存在周期性波动，需要先进行序列差分、季节差分才能输入至ARIMA 模型中进行处理，由于处理后的ARIMA 模型包含了季节差分参数，因此将其称为季节差分自回归移动平均模型，即SARIMA，记为SARIMA（p，d，q）（P，D，Q）s，由式（1）—式（5）所示：

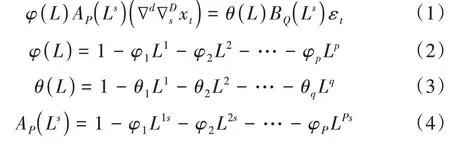
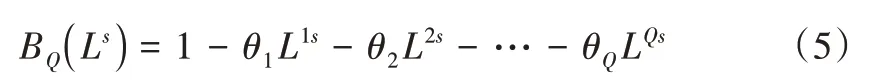
式中，p、q、d分别为非季节性自回归阶数、非季节性移动平均阶数及非季节性差分次数，P、Q、D分别为季节性自回归阶数、季节性移动平均阶数及季节性差分次数，s表示季节长度，εt为白噪声序列，L为滞后算子，xt为t时刻的客流量。

1.2 SARIMA模型构建

SARIMA 模型的建模过程主要可分为以下4个部分：

（1）数据平稳化。观察地铁客流历史数据，若存在明显非平稳趋势和季节性，可通过季节差分和序列差分法使序列转化为平稳序列，或采用扩充的迪基一富勒（Augmented Dickey-Fuller，ADF）检验对原始时间序列进行差分，并进行平稳性检验以确定差分阶数（d，D）。

（2）确定模型参数。利用自相关函数（Autocorrelation Function，ACF）图和偏自相关函数（Partial autocorrelation Function，PACF）图初步确定模型参数p、P、q、Q的取值范围。

（3）模型检验。利用赤池信息准则（Akaike Information Criterion，AIC）和贝叶斯信息准则（Bayesian Information Criterion，BIC）筛选同一个样本数据拟合参数p、P、q、Q分别在不同取值范围内存在的SARIMA 模型，并根据最小信息准则原则选取结果最优的模型。

（4）模型预测。

1.3 SVM模型

SVM 是机器学习中实际效果最好的分类算法之一，属于二分类模型，被定义为特征空间上间隔最大的线性分类器，其学习策略为间隔最大化，可转化为一个凸二次规划问题进行求解［27］。

SVM 设定存在分类超平面ωTx+b=0 能够将样本准确地划分为两类，与超平面平行的边界平面如式（6）所示：

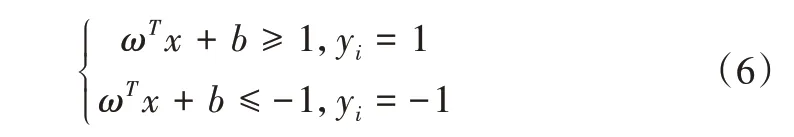
最优分类函数如式（7）所示：

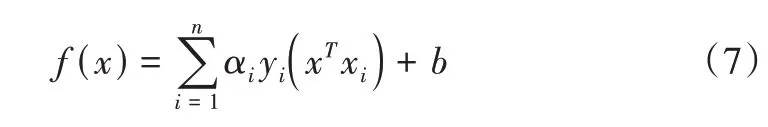
式中，xi为样本数据，ω为平面的法向量，b为参数，αi>0，i=1，2，…，n为拉格朗日系数，yi值取-1 或1。若数据不是线性可分的，则引入核函数对最优分类函数进行优化，如式（8）所示：

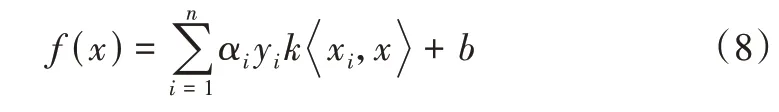
常见的核函数包括线性核函数、多项式核函数及径向基核函数（Radial Basis Function Kernel）。由于径向基函数在对面大样本或小样本数据、低维或高维数据、线性或非线性数据时，均具有良好的性能。并且，相较于多项式核函数，径向基核函数的参数更少。因此，本文采用径向基核函数进行实验，具体表达式如式（9）所示：

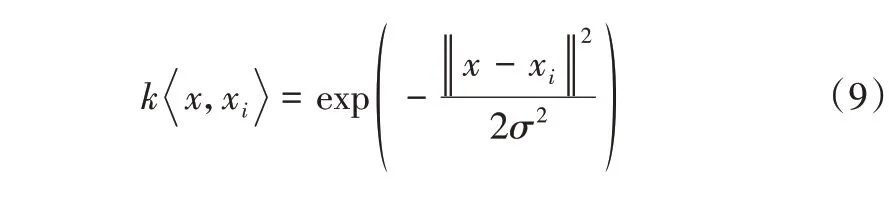
2 SARIMA-SVM 的地铁客流量预测模型

2.1 数据分类

根据西安4 号线7-8 月客流趋势图（见图1）可见，周一—周五的地铁客流趋势相对稳定，在双休日会出现异于前5 日的客流趋势。然而，以往研究将所有日期输入至模型中进行预测，造成预测结果较差。为此，本文将日期类型分为工作日和双休日，工作日指周一—周五共5 天，双休日指周六、周日2 天，并对这两种类型分别进行实验研究。

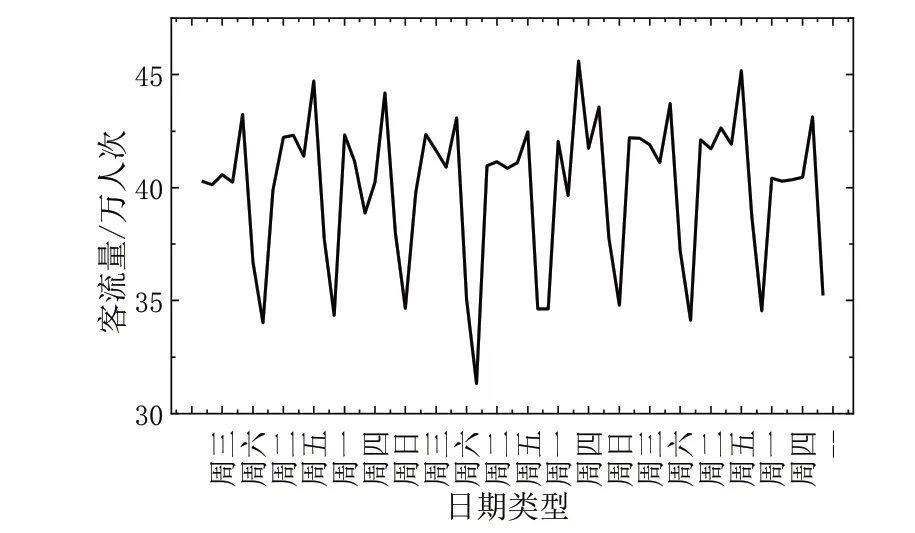
Fig.1 Passenger flow trend of Xi'an line 4 in July and August图1 西安四号线7-8月客流趋势图

2.2 数据处理

由于官方未公布完整的客流数据，导致在获取地铁客流信息和数据的过程中，收集到的数据存在空缺。为了解决该问题，通常利用删除、统计填充、预测填充、插值法等方法对数据进行预处理。其中，删除是最简单的处理方式，但只适用于数据集中缺失较少的情况；随机插值、牛顿插值及拉格朗日插值法是插值法填充最常用的3 种方法。由于牛顿插值法在增加额外插值点时，可利用之前的运算结果降低运算量，因此本文选取牛顿插值法对数据进行填充。

此外，节假日期间地铁出行人次增加，但节假日的客流数据既不属于工作日客流，也不能简单归于双休日客流。于是，将节假日客流定义为异常数据，进行删除处理。剩余客流数据按照工作日和双休日进行划分，将调休日客流划分为工作日客流。

2.3 预测模型

SARIMA 和SVM 的组合模型能够拟合客流数据中线性和非线性部分。其中，地铁客流量数据中的线性部分由SARIMA 模型进行拟合；SVM 模型则拟合SARIMA 模型残差中的非线性部分。模型拟合结果如式（10）所示：

式中，Zt为地铁客流量的实际值，Mt为SARIMA 模型拟合的线性部分，Nt为SVM 模型拟合的非线性部分，t=1，2，3，…，n。

2.4 模型构建

SARIMA-SVM 客流量预测模型结构由图2 所示，具体建模步骤为：

步骤1：对数据进行预处理。包括划分工作日和双休日客流数据、采用牛顿插值法补充数据缺失值、剔除节假日数据。

步骤2：构建SARIMA 预测模型。分别对工作日与双休日客流数据进行建模和预测，预测结果和预测残差{ηt}。

步骤3：构建SVM 模型。利用工作日和双休日客流预测残差数据分别构建SVM 模型并进行训练，使用网格搜索算法获取SVM 模型的最优参数，得到SVM 最优模型及SVM 模型的预测结果。

步骤4：将{ηt}导入训练好的SVM 模型中进行残差预测，得到预测结果

2.4 评价指标

选取平均绝对误差、均方误差及平均绝对误差百分比3 个指标检验各模型对地铁客流量的预测效果。具体的，平均绝对误差（Mean Absolute Error，MAE）表示实际值和预测值之间的误差绝对值的平均值，由式（11）所示；均方误差（Mean Square Error，MSE）表示实际值和预测值的相对误差，由式（12）所示；平均绝对误差百分比（Mean Absolute Percentage Error，MAPE）表示实际值跟预测值的绝对误差，由式（13）所示。

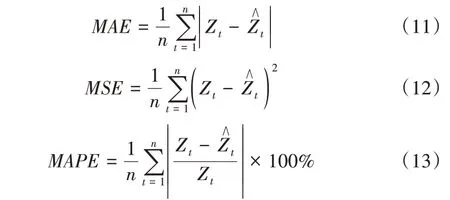
式中，n表示样本的数量，Zt为地铁客流的实际值为地铁客流的预测值。

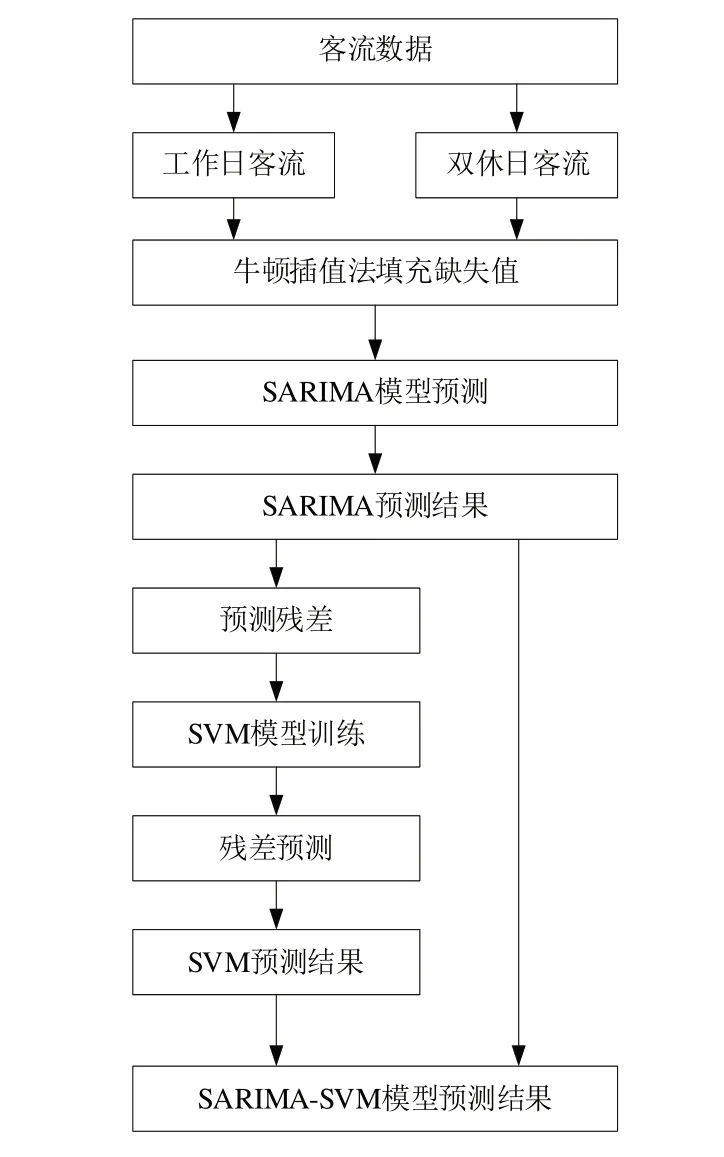
Fig.2 SARIMA-SVM model structure图2 SARIAM-SVM 模型结构

3 实验结果与分析

3.1 数据来源

考虑到数据的完整性，以西安市2019 年1 月14 日—2020 年1 月13 日地铁4 号线每日客流量为例，共收集客流数据365 条，客流量单位为万人次/日，数据来源于西安地铁运营分公司运营日报。经过数据处理后，共得到250 条工作日客流数据，88 条非工作日客流数据，非节假日数据338条。

3.2 预测效果

3.2.1 工作日地铁客流

（1）SARIMA 模型。将2019 年1 月14 日—2020 年1月13 日中250 条工作日客流数据作为实验数据。在观察客流数据图时发现，工作日地铁客流数据存在明显的季节规律。因此，设置SARIMA 模型的季节参数为5。首先，经过一次季节差分及序列差分后获得平稳的时间序列；然后，根据PACF 图和ACF 图选取合适的p、q、P、Q阶数范围进行试算；最后，根据信息准则最小原则进行定阶。实验最终确定p=5、q=2、P=1、Q=0，预测模型为SARIMA（5，1，2）（1，1，0，5），具体预测结果见表1、表2。

（2）SVM 模型。在2019 年1 月14 日—2020 年1 月13日的工作日客流数据中随机抽取200 条数据作为训练集，剩余数据作为测试集。首先，根据式（14）对数据进行归一化处理：

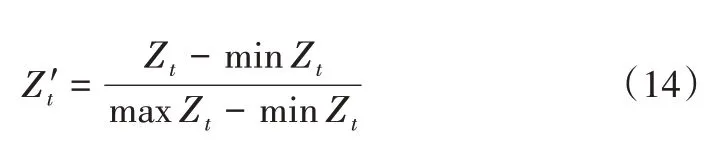
式中，Zt为客流实际值，minZt为客流最小值，maxZt为客流最大值，Z't为归一化后的客流值。

然后，利用sklearn 中的网格搜索方法GridSearchCV 寻找SVM 最优模型参数，确定最优的参数组合为惩罚参数c=0.2，核函数gamma=3.3。

最后，根据式（15）对SVM 模型预测的结果进行反归一化：

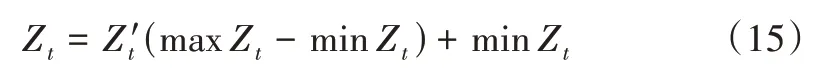
如此，模型才能最终输出所需要的客流预测结果，具体预测结果及指标检验结果见表1、表2。

（3）SARIMA-SVM 模型。在2019 年1 月14 日—2020年1 月13 日工作日客流数据中随机抽取200 条数据作为训练集，剩余数据作为测试集，SVM 模型参数为c=0.01，gamma=0.001。具体模型预测结果及指标检验结果见表1、表2。

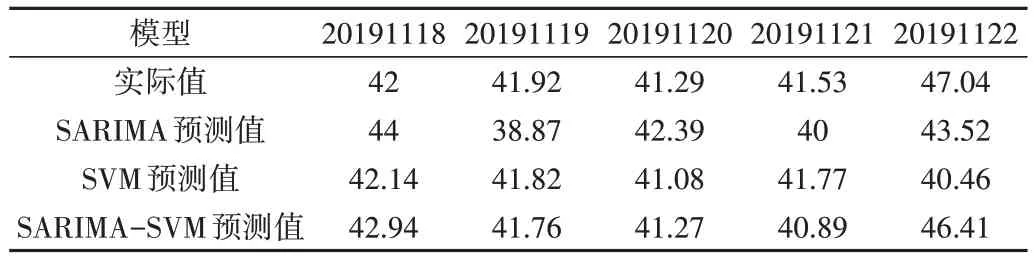
Table 1 Forecast results of the three models in weekdays表1 工作日三种模型的预测结果 （万人次）

Table 2 Comparison of prediction error indexes of the three models in weekdays表2 工作日三种模型的预测误差指标比较

3.2.2 双休日地铁客流预测

（1）ARIMA 模型。将2019 年1 月14 日—2020 年1 月13 日中88 条双休日客流数据作为实验数据。在观察双休日的客流没有明显的季节变化后，只进行一次序列差分计算，即d=1。利用AIC 和BIC 准则定阶后的模型为ARIMA（2，1，2），模型预测结果及指标检验结果见表3、表4。

（2）SVM 模型。相较于工作日SVM 预测模型，采用径向基函数作为核函数，通过网格搜索得到的最优参数组合惩罚系数c=0.3，核函数gamma=1.1，模型预测结果及指标检验结果见表3、表4。

（3）ARIMA-SVM 模型。在2019 年1 月14 日—2020年1 月13 日中88 条非工作日客流数据中随机抽取52 条数据作为训练集，剩余数据作为测试集，且分别构建训练集和测试集的对应序列{ηt}，SVM 模型参数精选后结果为c=1，gamma=2，模型预测结果及指标检验结果见表3、表4。

3.2.3 不考虑日期类型的SARIMA-SVM 预测模型

将2019 年1 月14 日—2020 年1 月13 日收集到的338天数据全部作为实验数据，直接进行建模。SVM 模型参数为c=0.01，gamma=2，模型检验指标见表5。

图3、图4 分别为工作日与双休日时，SARIMA 模型、SVM 模型、组合模型的预测值与实际值的区别。

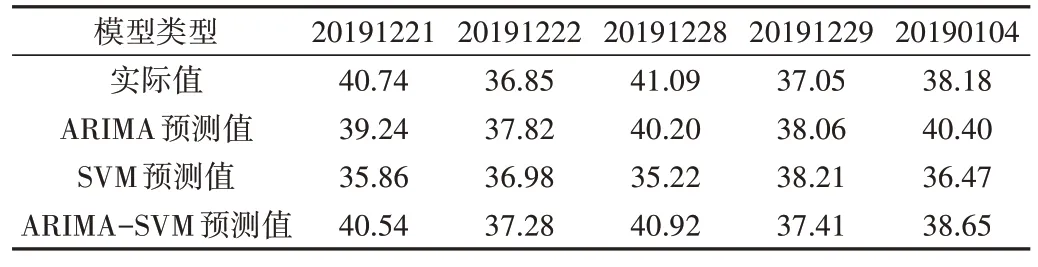
Table 3 Forecast results of the three models in weekends表3 双休日三种模型的预测结果 （万人次）

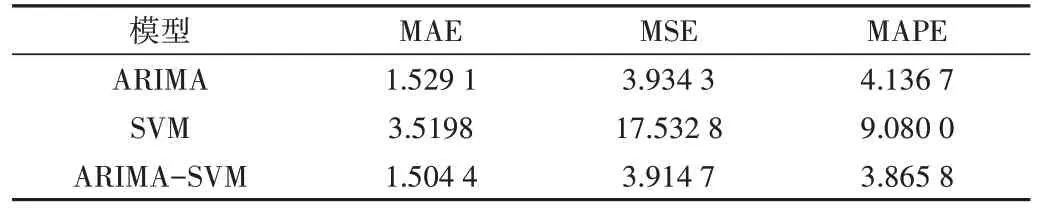
Table 4 Comparison of prediction error indexes of the three models in weekends表4 双休日三种模型的预测误差指标比较

Table 5 Comparison of prediction error indexes of two combined models表5 两种组合模型的预测误差指标比较

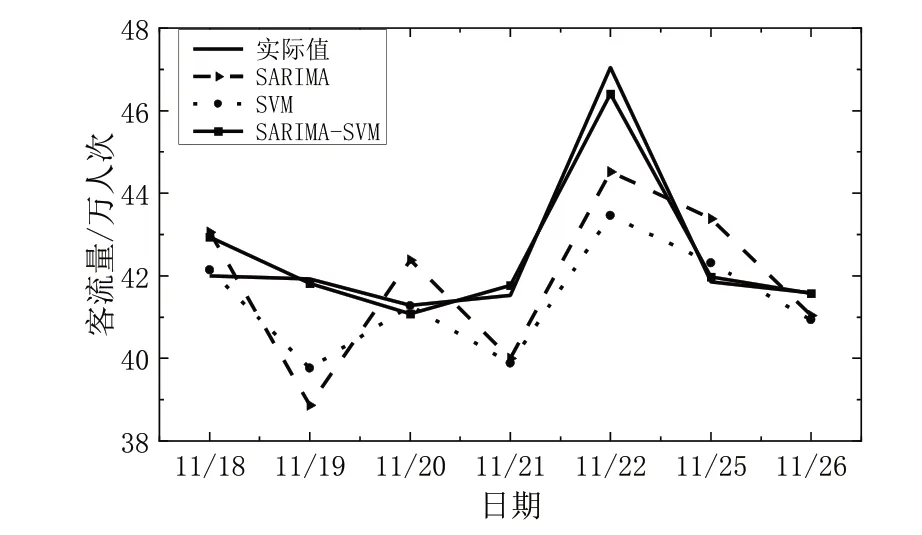
Fig.3 Comparison of prediction results of various models of subway passenger flow on weekdays图3 工作日地铁客流各模型预测结果比较

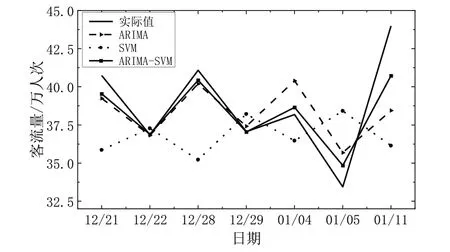
Fig.4 Comparison of prediction results of various models of subway passenger flow on weekends图4 双休日地铁客流各模型预测结果比较

由表1、表2 和图3 可见，地铁工作日客流局部存在线性特征，整体上呈现为非线性特征；SARIMA 模型预测结果曲线与实际值曲线相近，能够较好拟合线性特征，非线性特征通过以时间为参照的客流统计得到了一定程度的消减。

根据预测误差指标最小原则，SVM 模型在非线性预测中展现了优秀的拟合能力，与SARIMA 模型能够有效互补。此外，相较于单一模型，组合模型的误差指标更小，优势显著。

由表3、表4 和图4 可见，在预测双休日客流时，组合模型相较于单个模型的MAPE 值更低；考虑日期类型的组合预测模型相较于其它模型，3 个检测指标值均有所减少，证明划分工作日与非工作日建模有助于提高模型预测精度。

4 结语

本文分析地铁日客流量在各日期类型中存在的不同特点，结合SARIMA 和SVM 方式拟合地铁客流量的线性和非线性特征。通过与单一模型的比较发现，组合模型在工作日时，预测精度相较于SARIMA 模型、SVM 模型分别提高23.39%、15.43%；在双休日时，分别提高1.62%、57.26%。实验数据表明，SARIMA 和SVM 的组合模型预测准确率更高，基本达到交通客流的预测要求，能够为轨道交通运营提供一定的参考。

但由于地铁客流不仅存在周客流规律，还具有日客流规律，后续将采取更小的时间粒度对客流进行划分与预测。此外，由于影响客流规律的因素众多，本文仅以工作日和双休日对数据进行划分，尚未能完全体现客流的真实规律，后续也将引入多种因素进行建模，以获得更高的预测精度。