基于多源数据聚类与奇异值分解的混合推荐算法

刘伟友，吴 陈

（江苏科技大学计算机学院，江苏镇江 212100）

0 引言

在互联网深度融合和大数据蓬勃发展的时代背景下，信息资源呈现爆发式增长，由此带来信息过载、用户需求不明确等问题［1］。目前，应对这些问题的主要手段包括搜索引擎和推荐系统。其中，搜索引擎可对信息资源进行过滤、筛选，但当用户难以键入需求时，搜索引擎便无法发挥作用；推荐系统则是一种智能化应用软件，旨在满足用户当前最需要或最感兴趣的信息［2］，即使在用户需求不明确的情况下，也能提供持续、有效的个性化推荐服务，因而具有巨大的应用优势和商业价值，被广泛运用于新闻、音乐、视频和电商等领域，例如谷歌新闻［3］、网易云音乐、Netflix网络流媒体、Amazon 电商等。

推荐算法作为推荐系统的核心引擎，是专家学者研究的热点与重点，主要可分为基于内容的推荐算法、基于协同过滤（Collaborative Filtering，CF）的推荐算法和混合推荐算法［4］。具体的，基于协同过滤的推荐算法是影响最深远、应用最广泛的传统推荐算法，最早可追溯至1992 年Goldberg 等［5］设计的Tapestry 电子邮件过滤系统，但由于算法的输入数据通常呈现高维性和稀疏性，存在准确性、实时性、可扩展性不足等问题［6-7］。为此，刘晴晴等［8］采用奇异值分解（Singular Value Decomposition，SVD）算法分解、填充评分矩阵，有效缓解数据稀疏问题，但传统SVD 算法并未考虑用户评分习惯和上下文环境因素，预测评分效果一般。张阳等［9］提出一种融合用户显式反馈和隐式反馈的SVD++自适应推荐算法，但算法实时性较差。Frémal 等［10］利用组合聚类算法对项目特征进行聚类。Chen 等［11］根据群体智能思想划分用户群组，加快查找最近邻居的时间，提升算法实时性，但忽视输入数据自身稀疏性。

由此可见，仅使用单一算法推荐存在明显的性能瓶颈，目前往往混合使用多种推荐算法解决该问题。例如，魏浩等［12］先对用户进行聚类得到近邻用户集，再取用户集的平均评分填充稀疏矩阵，最后使用SVD 算法分解重构矩阵产生推荐结果。刘超等［13］利用改进BiasSVD 算法预测评分，对用户进行聚类并调整预测偏差。Nilashi 等［14］结合主成分分析（Principal Component Analysis，PCA）、自组织映射（Self-Organizing Map，SOM）和期望最大化（Expectation Maximization，EM）技术构建旅游推荐系统。以上混合推荐算法兼顾了数据稀疏性问题和算法准确性要求，但均未解决用户冷启动问题［15］，且无法反映用户兴趣变化造成的评分影响。

为此，本文提出一种基于多源数据聚类和奇异值分解的混合推荐算法，主要贡献包括：①提出一种从多源数据中充分挖掘并有效整合用户信息的处理办法，改善传统K-means 聚类算法输入数据单一的问题，提升算法推荐准确性，在一定程度上缓解了用户冷启动问题；②定义一种新的时间衰减函数改进预测评分计算公式和BiasSVD 算法的损失函数，以反映用户兴趣变化对电影评分造成的影响；③将基于多源数据的K-means 聚类算法和融合时间衰减函数的BiasSVD 算法相互结合，通过实验选取模型最佳参数进行比较，分析两种改进因素各自的作用效果和本文所提出算法的推荐性能。

1 相关工作

1.1 K-means聚类算法

由于用户—项目评分矩阵具有高维性和稀疏性特性，首先引入K-means 聚类算法［16］对用户进行聚类，以此构建多个较低维的用户类簇评分矩阵。如此，一方面可减少系统内存消耗，加快后续矩阵分解计算，提升算法整体运行效率；另一方面，基于相似度较高的用户类簇进行评分预测，推荐结果更准确。

聚类是将一个数据集合划分为多个由相似数据对象组成的子集合（即类簇）的过程，每一个数据对象和本类簇的其它数据对象相似，但与其它类簇的数据对象相异。Kmeans 算法是一种简单、有效的聚类算法。其中，K 为要划分的类簇数目，即质心个数；means 代表类簇中全部数据对象的均值，数据对象之间的相似度通过彼此的距离来衡量，距离越小表明数据对象之间相似度越高，越应该被划分至同一类簇。K-means 算法具体过程如算法1所示。

算法1K-means 聚类算法

1.2 词频—逆文档频率公式

为评估用户对某一类型项目的喜爱偏好程度，利用词频—逆文档频率（Term Frequency-Inverse Document Frequency，TF-IDF）公式［17］对该指标进行评估：

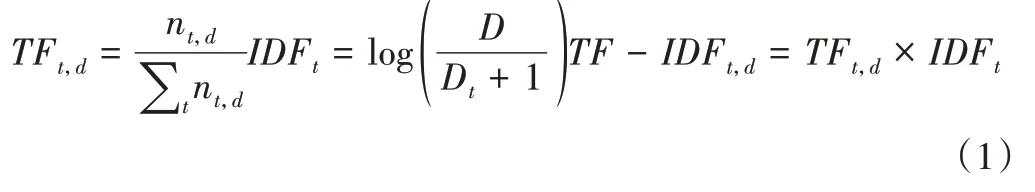
其中，t为文档d中的某一词条，TFt，d为词条t在文档d中出现的频率，nt，d为词条t在文档d中出现的次数表示文档d的总词数，IDFt为词条t在文档总集中的逆文档频率，表示词条t的普遍程度，D为文档总集中的文档总个数，Dt为文档总集中包含词条t的文档个数，将两者相乘可得到词条t的词频—逆文档频率TF-IDFt，d。

由式（1）可知，当某一词条在某篇文档出现的频率越高（即TF值越大），且在文档总集中被较少的文档包含（即IDF值越大）时，TF-IDF值越大，说明该词条越重要。

1.3 SVD算法

基于协同过滤的推荐算法包含基于用户和基于物品的传统协同过滤推荐算法及基于模型的推荐算法。基于模型的推荐算法将机器学习的思想运用到推荐算法中，主要包括矩阵分解算法、图模型算法、隐语义模型算法、神经网络算法等。其中，矩阵分解算法［18］由于易于实现且可扩展性好被普遍使用。

本文采用矩阵分解算法对稀疏的用户—项目评分矩阵进行降维处理，由此得到用户和项目的多维隐式特征向量，并利用随机梯度下降算法产生预测评分，进而填充稀疏评分矩阵。现有矩阵分解算法有很多种，奇异值分解（SVD）算法［19］最为经典，该算法主要将评分矩阵R分解为3个低维矩阵乘积，计算公式定义如下：

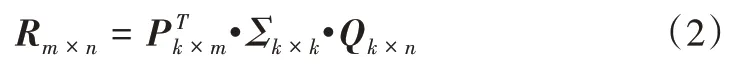
其中，Rm×n为评分矩阵为用户隐式特征正交矩阵的转置，Qk×n为项目隐式特征正交矩阵，Σk×k为奇异值对角矩阵。

然而，SVD 计算过程非常复杂，且运用SVD 的前提是Rm×n是稠密的，但推荐系统中Rm×n往往非常稀疏。为此，Simon［20］提出一种FunkSVD 算法，将评分矩阵R近似分解为两个低秩矩阵乘积的形式，计算公式如下：

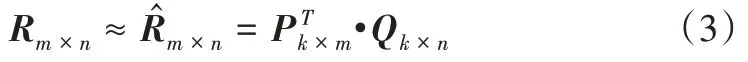
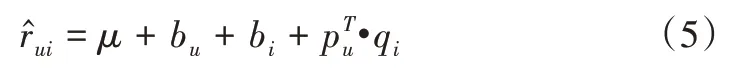
其中，μ为所有用户对所有项目评分的均值，bu为用户评分的偏置，bi为项目被评分的偏置。

2 混合推荐算法

2.1 数据预处理

传统K-means 聚类算法的输入通常为用户—项目评分数据，但该输入的基本假设是推荐系统已经运行了一段时间，采集到用户和项目之间的显式和隐式反馈数据。为进一步提高推荐算法准确性，缓解推荐系统用户冷启动的问题，结合基于人口统计学的推荐和基于内容的推荐的算法思想，对传统K-means 聚类算法的输入数据进行改进。

以MovieLens 数据集为例，改进后的K-means 聚类算法在用户—电影评分数据的基础上增加了用户特征数据和电影类型特征数据。为此，对于输入的多源数据，首先要进行以特征工程为主的数据预处理，具体操作如下：

（1）特征选择。例如，去除电影的来源网址数据。

（2）连续数值型特征的归一化和离散化。例如，将用户年龄从小到大划分为7个年龄阶段。

（3）非数值型特征采用One-Hot 编码。例如，将用户性别采用［0］、［1］进行编码；将电影分为19 种类型，按照类型假定的先后顺序分别用［0］、［1］进行编码。

数据预处理完成后，可得到用户特征矩阵A、用户—电影评分矩阵R和电影类型特征矩阵B：

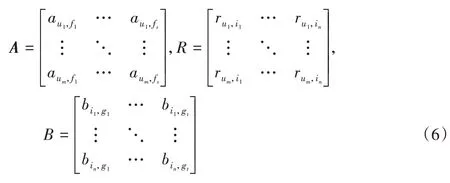
其中，um表示第m位用户，fs表示用户的第s个特征，表示第m位用户在第s个特征上的取值，in表示第n部电影，gt表示电影的第t种类型特征表示第n部电影在第t种类型特征上的取值，该值为0 时，代表电影in没有类型特征gt。由于某些电影包含多种类型，因此表示第m位用户对第n部电影的评分，该值取[1，5]内的整数。

此外，用户对电影的喜好除了直接通过用户对某电影的评分进行衡量，还可通过用户观看某类型电影的个数进行体现。因此，对用户—电影评分矩阵R进行统计处理可得到用户—电影观看矩阵R'，在此基础上，结合电影类型特征矩阵B并利用TF -IDF 公式可得到用户—电影偏好矩阵H。R'和H的形式分别定义如下：

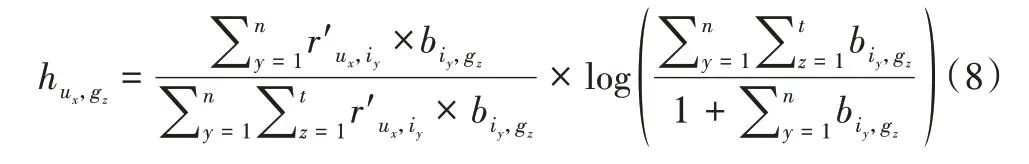
其中，被乘数的分子表示用户ux观看过的电影中含有类型gz的电影总数，分母表示用户ux观看过的电影中各个类型的电影个数的和，log 中的分子表示所有电影中各个类型的电影个数之和，分母表示所有电影中含有类型gz的电影总数。由式（8）可知，当某一类型电影在某用户的观看列表中出现的频率越高，且包含该类型的电影在所有电影中占比较小时，对应的值越大，说明该用户更偏爱此类型电影。

最后，合并用户特征矩阵A，用户—电影评分矩阵R和用户—电影偏好矩阵H可得到用户矩阵W，定义如下：

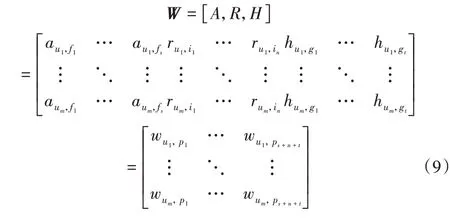
2.2 基于多源数据的K-means聚类算法

传统的K-means 聚类算法中距离包括欧氏距离及余弦相似度。其中，欧氏距离反映的是向量各维度数值上的绝对差异性，余弦相似度反映的是向量整体方向上的相对差异性。由于本文算法输入包含较多的非数值型特征，例如用户性别、电影类型等信息，采用余弦相似度更能刻画两个用户特征向量之间的相似程度。余弦相似度定义如下：

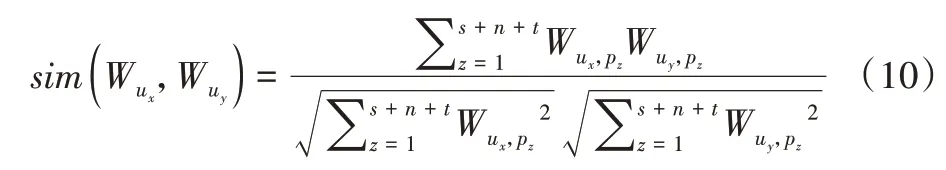
多源数据的K-means 聚类算法如算法2，对应的算法流程图如图1所示。

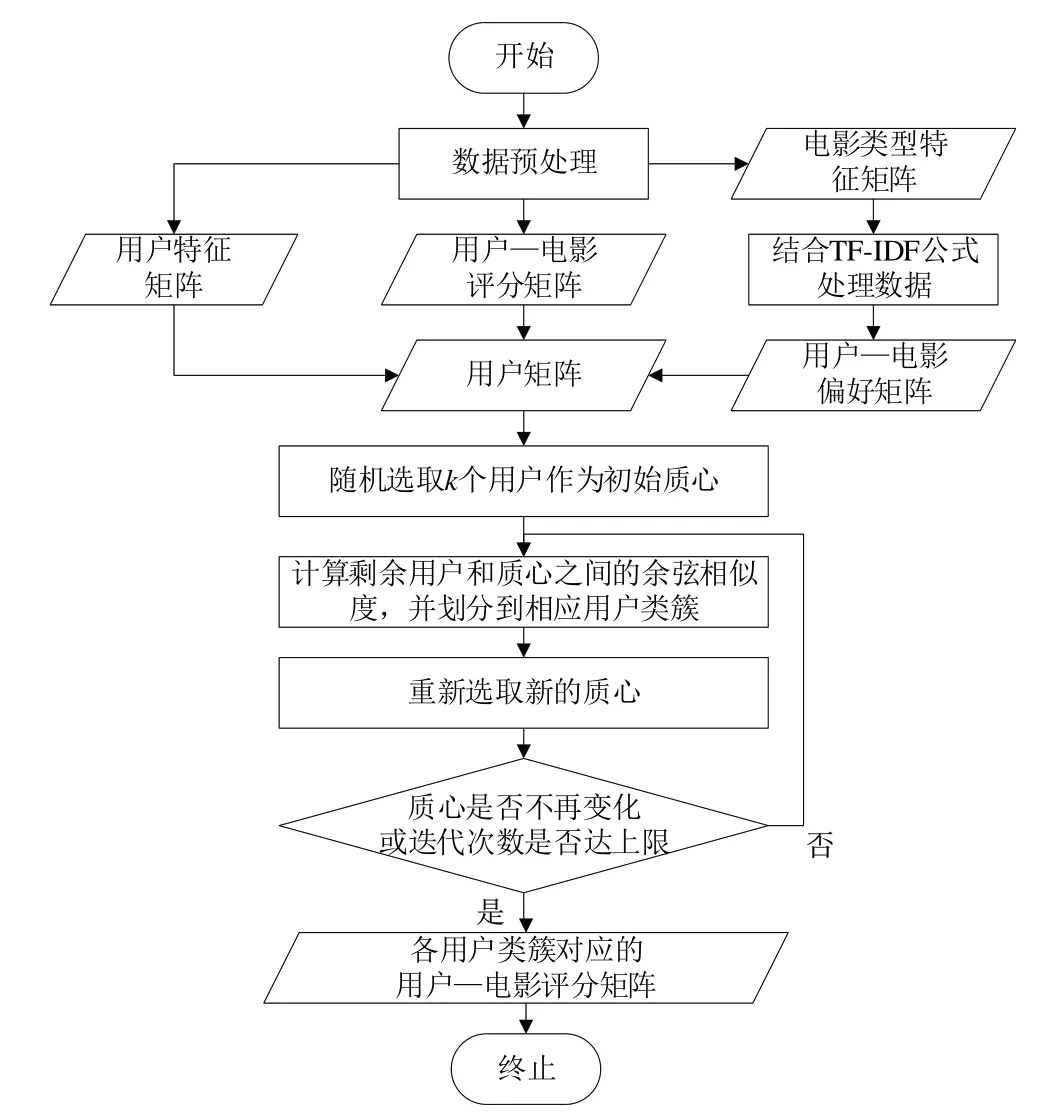
Fig.1 Flow chart of K-means clustering algorithm based on multisource data图1 基于多源数据的K-means聚类算法流程图

算法2基于多源数据的K-means 聚类算法

2.3 融合时间衰减函数的BiasSVD算法

一般情况下，用户对电影的兴趣并非一成不变，而随着时间发生变化。相较于用户早期观影行为，用户近期观影行为更能反映用户当前的兴趣。

然而，传统BiasSVD 算法并未考虑时间因素的影响，无法反映用户兴趣的变化。因此，本文引入一种时间衰减函数对该算法进行优化：

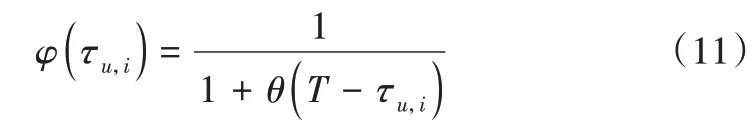
其中，τu，i为用户u对电影i评分时的时间，T为系统当前时间，θ为时间衰减参数，根据推荐系统中用户兴趣变化的快慢程度自行设定。如果用户兴趣变化较快，则θ取较大数值；反之，θ取较小数值。鉴于用户观影兴趣变化较慢，本文θ取较小数值。

其中，μ为所有用户对所有项目评分的均值，bu为用户评分的偏置，bi为项目被评分的偏置，β为调节参数，qi，l(τu，i)表示时间衰减函数φ(τu，i)对电影i的隐式特征l的影响程度。可得融合时间衰减函数的BiasSVD 的损失函数为：

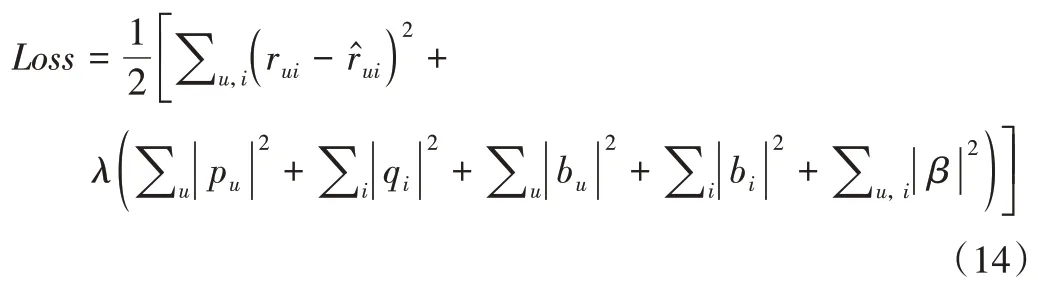
其中，Loss前半部分为平方误差项，后半部分为正则化项，λ为正则化系数，设学习率为α，分别对pu、qi、bu、bi和β求偏导，根据随机梯度下降算法的思想，可得如下递推公式：

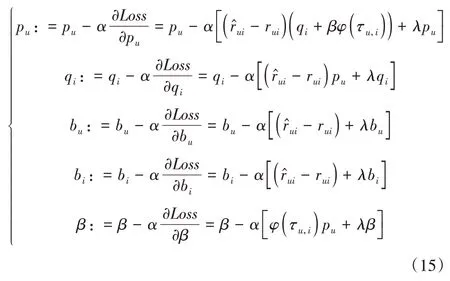
2.4 混合推荐算法

结合多源数据的K-means 聚类算法与融合时间衰减函数的BiasSVD 算法，可发挥两种算法的各自优势。混合推荐算法如算法3所示：

算法3基于多源数据聚类和奇异值分解的混合推荐算法

3 实验结果与分析

3.1 数据集

采用美国明尼苏达大学收集整理的MovieLens-100k公开数据集进行实验［22］，该数据集的评分数据整体稀疏度约为93.70%，属于高维稀疏矩阵。其中，文件u.item 为电影属性数据，主要包含电影ID、电影名称、发布日期、电影类型4 个字段；文件u.user 为用户人口统计学数据，主要包含用户ID、年龄、性别、职业4 个字段；文件u.data 为用户—电影评分数据，包含用户ID、电影ID、电影评分、时间戳4个字段。每位用户至少对20 部电影进行评分，评分取[1，5]内的整数值，评分越高表明用户对该电影越喜爱。实验采用5 折交叉验证法，最终实验结果取多次实验的平均值。

3.2 评测指标

采用平均绝对误差（MAE）评估用户实际评分与算法预测评分之间的差异，计算公式如下：

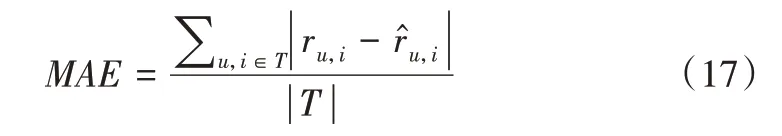
其中，|T|为测试集中的评分总数分别为用户u对电影i的实际评分和预测评分。MAE越小，说明模型预测评分与用户实际评分越接近，算法预测评分准确度越高。

晨读时，我发现教室内空位很多，一问才知道，两人在机房准备余姚市编程复赛，三人在书法教室准备校书法比赛，两名校男足队员正在操场训练……一日之计在于晨，见到这种情形，班主任兼语文老师的我是不是该着急了呢？更着急的是家长，眼看再过半年多就要毕业了，先后好几位家长都十分担心地问我：参加这些活动会不会影响孩子的成绩？

采用精确率（Precision）和召回率（Recall）评价算法的推荐性能，计算公式如下：

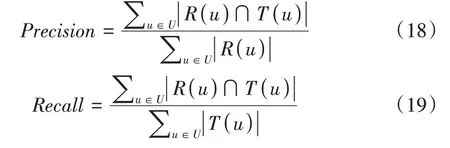
其中，R(u)表示训练集中为用户u生成的推荐列表，T(u)表示测试集中用户u实际的兴趣列表。Precision值越高，说明推荐列表中用户喜欢的电影部数占推荐列表总数的比例越高；Recall值越高，说明推荐列表中用户喜欢的电影部数占用户喜欢的电影总数的比例越高。

采用F_measure对Precision、Recall的值进行调和，计算公式如下：

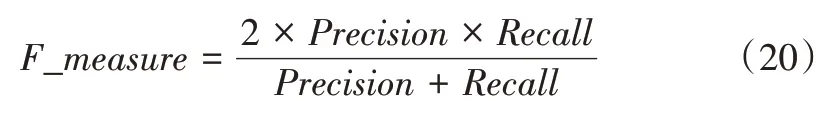
3.3 参数选取

为了使算法取得最佳效果，首先对相关参数进行调节。具体参数包括聚类质心个数k、隐式特征维度K、学习率α、最大迭代次数svd_max_iter和推荐列表长度N。由于α和svd_max_iter对推荐算法的性能影响较小，根据以往经验，先取α=0.02、svd_max_iter=100 并结合评测指标进行控制变量实验。

为了确定聚类质心个数k的最优取值，固定K=5、N=3观察k的取值变化对MAE的影响，结果如图2所示。

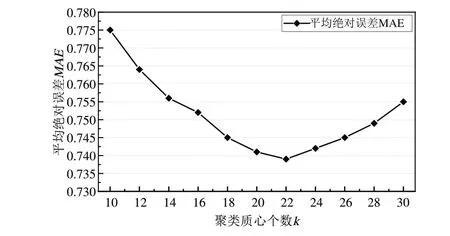
Fig.2 The influence of different clustering number k on MAE图2 聚类质心个数k对平均绝对误差MAE的影响

由图2 可见，随着k取值不断增大，MAE先递减后递增，在k=22 处取得最小值，故选取k=22 作为聚类的质心个数。

由于隐式特征维度K的大小直接影响到重构后评分预测的准确度，K过小会导致原评分矩阵信息损失严重，最终预测误差大；K过大会导致算法的时间和空间复杂度过高。为此，设定k=22、N=30 评估K对MAE值的影响，结果如图3所示。

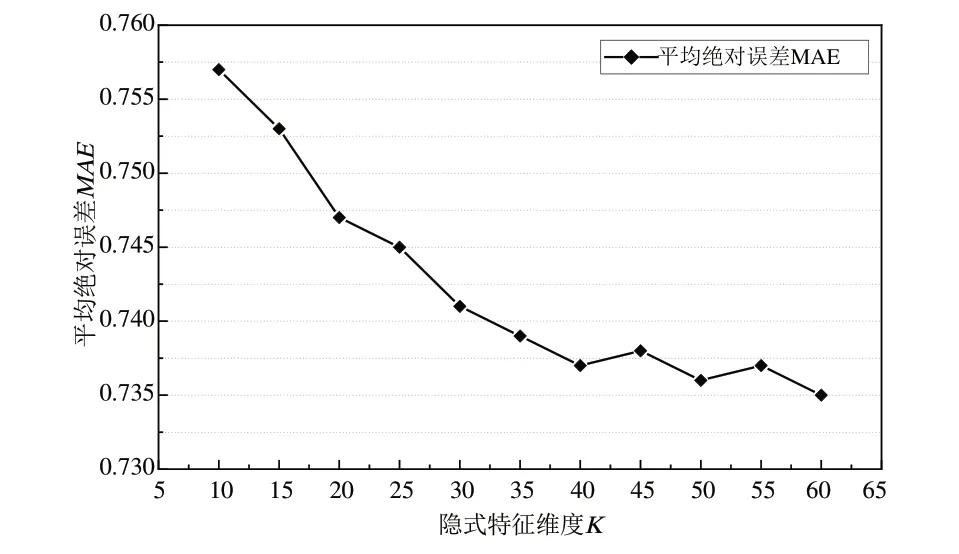
Fig.3 The influence of different implicit feature dimension number K on MAE图3 隐式特征维度K对平均绝对误差MAE的影响

由图3 可见，当K<40 时，MAE随着K的增大而下降；当K≥40 时，MAE的下降趋势趋于平缓。综合考虑算法准确度、时间复杂度和空间复杂度等方面的要求，设定K=40。

为了确定学习率α和最大迭代次数svd_max_iter，实验采取调节学习率α，记录算法收敛时的迭代次数Steps和MAE分析α的取值，结果如表1所示。

Table 1 The influence of different learning rate α on iterations number Steps and MAE表1 学习率α对迭代次数Steps和平均绝对误差MAE的影响

由表1 可知，在0.010～0.031 内，以0.003 递增调节α的过程中，当α=0.016 时迭代次数最少，算法收敛最快，对应的MAE也相对较小。

在 确 定k=22、K=40、α=0.016、svd_max_iter=90后，研究推荐列表长度N对算法精确率Precision和召回率Recall的影响，并结合F_measure选取最佳N值，结果如图4所示。

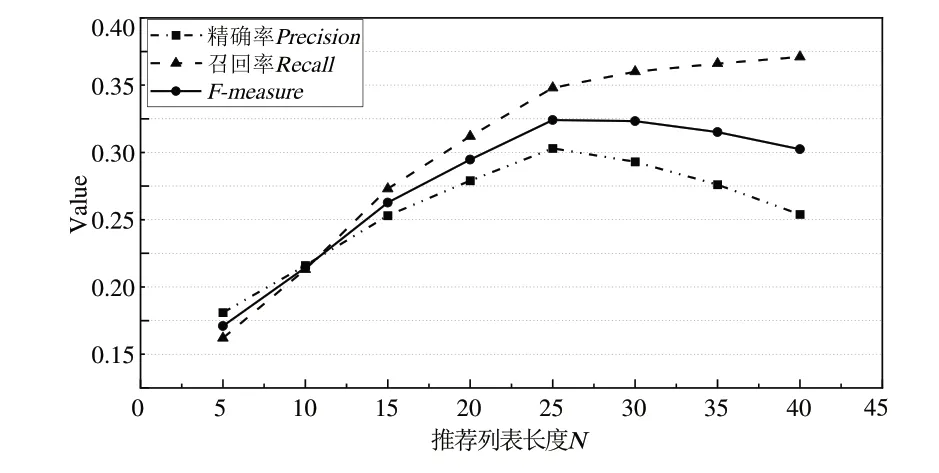
Fig.4 The influence of different recommended list length N on Precision，Recall and F-measure图4 推荐列表长度N对精确率Precision、召回率Recall和F-measure值的影响

由图4 可见，随着N值的不断增大，Precision先增大后逐渐减小，而Recall则不断上升。当N∈[25，30]左右时，F_measure最大，当N=27，此时综合推荐性能最佳。

根据上述实验结果表明，本文算法的模型最佳参数分别为k=22、K=40、α=0.016、svd_max_iter=90、N=27。

3.4 实验比较

采用MovieLens-100k 公开数据集，将本文提出的混合推荐算法（MC-TimeSVD）与只考虑单一改进因素的基于多源数据的K-means 聚类协同过滤推荐算法（MCKMeans）、融合时间衰减函数的BiasSVD 协同过滤推荐算法（TimeSVD）、传统基于K-means 聚类的协同过滤推荐算法（K-Means）和基于SVD 的协同过滤推荐算法进行比较。具体结果如表2所示。

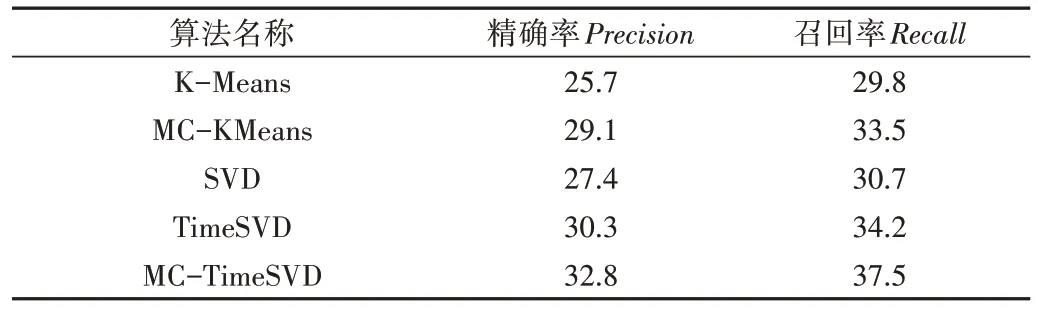
Table 2 The best precision and recall of each algorithm表2 5种算法各自最佳的精确率Precision和召回率Recall（%）

由表2 可知，相较于传统K-Means 推荐算法，MCKMeans 推荐算法在Precision和Recall分别提升3.4%和3.7%，证实从多源数据中充分挖掘并有效整合用户信息能够改善用户聚类效果，缓解用户冷启动问题；相较于传统SVD 推荐算法，TimeSVD 推荐算法在Precision和Recall上分别提升2.9%和3.5%，证实融合新的时间衰减函数能够较好反映用户兴趣的变化对电影评分造成的影响；相较于SVD 推荐算法，MC-TimeSVD 混合推荐算法在Precision和Recall上分别提升5.4%和6.8%，证实MC-TimeSVD 混合推荐算法能够较好结合两者算法的各自优势，有效提升了推荐综合性能。

相较于综合考虑两种改进因素的MC-TimeSVD 混合推荐算法，只考虑单一改进因素的MC-KMeans 推荐算法和TimeSVD 推荐算法在Precision和Recall上分别下降3.7%、4.0%和2.5%、3.3%，既证实MC-TimeSVD 混合推荐算法的推荐性能是两种改进因素共同作用的结果，又说明MC-KMeans 推荐算法对混合推荐算法性能提升的作用更大。

4 结语

本文提出基于多源数据聚类和奇异值分解的混合推荐算法，以提升算法的推荐性能，缓解用户冷启动问题。该算法将用户属性数据、用户—电影评分数据和项目属性数据作为输入数据，较好地缓解了用户冷启动问题，并且引入改进的K-means 聚类算法和时间衰减函数的BiasSVD算法的优势。实验结果表明，以上改进方法均提升算法的综合推荐性能，但仅集中在一个用户全特征矩阵处理多源数据，后续将从多视图聚类和模型结构优化角度进行研究。