基于EMD的铁磁性物质检测研究
2023-01-02董建荣李丕丁
董建荣,李丕丁,王 成
(上海理工大学健康科学与工程学院 上海 200093)
0 引言
核磁共振成像(Magnetic Resonance Imaging,MRI)作为临床诊断的主要成像技术[1],在工作过程中会产生强磁环境(0.2-3T),容易受铁磁性物质影响,甚至对被测试者身体安全产生危害。因此,必须对所有进入MRI 工作环境中的人员进行铁磁性物质检测。
磁异常探测(Magnetic Anomaly Detection,MAD)作为一种被动探测技术,通过分析目标物体磁性特征在环境磁场中产生的磁异信号检测目标物体。现已被广泛应用于航空探浅、水下铁磁性物质探测、地震预测、医学核磁共振等领域[2]。目前,MAD 技术已与多种算法相结合,例如Pradhan 等[3]提出基于正交基函数的匹配滤波方法(Orthogonal Basis Functions,OBF),将磁异信号表示为3 个正交函数的线性组合匹配滤波。王磊等[4]提出基于自回归(Auto Regression,AR)模型的白化滤波器,现将测量信号滤波处理,然后进行OBF 检波,最后利用最小熵检测法(Minimum Entropy Detector,MED)和高阶过零检测法(High Order Croossing,HOC)检测较低信噪比条件下的磁目标。
然而,以上方法均建立在背景噪声不变的前提下进行实验,OBF 还需要获取测量信号的先验信息。为解决以上问题,Nezhadshahbodaghi 等[5]提出基于能量检测器的非抽样离散小波变换法(Undecimated Discrete Wavelet Transform,UDWT)。该算法无需测量信号任何先验信息即可直接检测磁异信号,但由于小波分析首先需要确定小波基,因此对不同特性目标信号,可能显示不同性能。此外,针对非线性、非平稳性复杂信号,Inturi 等[6]提出经验模态分解方法(Empirical Mode Decomposition,EMD),该方法将信号分解成多个固有模态函数(Intrinsic Mode Function,IMF)以表征信号的基本信息,根据磁异信号特征自适应调整分析精度,无需信号的任何先验信息和对背景噪声进行假设。
虽然MAD 方法已在各领域广泛应用,但在核磁共振成像领域鲜有研究。为此,本文采用MAD 方法检测MRI工作环境中的铁磁性物质。在基于磁通门传感器的铁磁性探测系统基础上,特征分析探测的铁磁性物质产生的磁异信号,并使用EMD算法从强噪声背景中提取目标磁异信号。
1 磁异常探测模型
本文设计磁探测系统处于静止状态,检测移动中的铁磁性目标物质,假设铁磁性目标物体以恒定速度V沿直线运动经过磁探测系统,磁矩m在方向上和大小上恒定,CPA(closest proximity approach)为目标物体距离磁探测系统的最小距离,当目标物体移动到CPA 位置附近,获得的目标信息最丰富。磁异常探测模型[7]如图1所示。
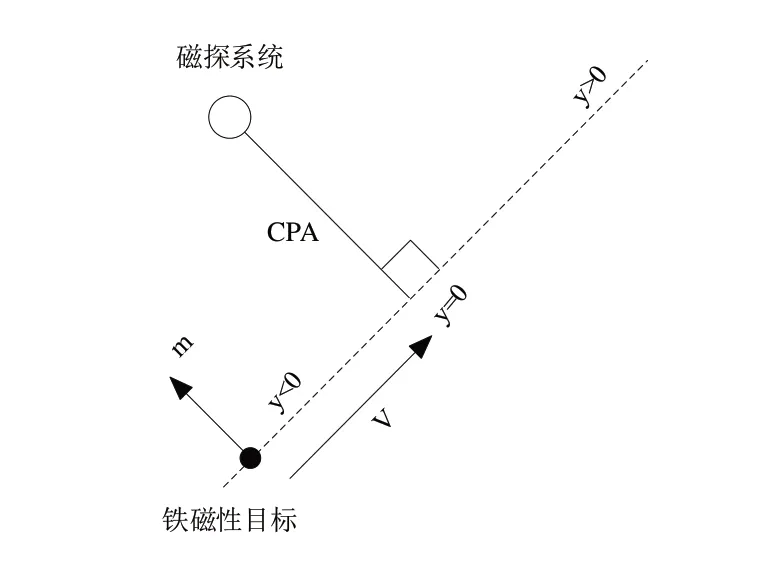
Fig.1 Model of magnetic anomaly detection图1 磁异常探测模型
由于地磁场作用,铁磁性物质会在区域范围内地磁场Be中产生扰动磁场Bi,从而产生磁场异常信号Ba,三者间的矢量关系如式(1)所示:

当铁磁性目标物体直径远小于其与磁探测系统的距离时,目标磁场可等效于磁偶极子磁场[8]。根据毕奥萨伐尔定律,在远离磁矩m(目标)处(距离为R)所产生的磁感应强度Bm可表示为:

式中,m为偶极子磁矩,单位为A·m2,真空磁导率μ=4π× 10-7H/m,R为目标物体与磁探测系统间的距离。因此,探测的磁异信号S可近似表示为磁偶极子场Bm在地磁场T(T>>Bm)上的投影[8]:

根据式(3),采用MATLAB 仿真软件对磁异信号的等价模型进行模拟。考虑到地磁矢量在实际应用中变化范围有限,因此设为不变量[9],磁异信号仿真波形如图2所示。

Fig.2 Magnetic anomaly signal simulation waveform图2 磁异信号仿真波形
当检测到磁异信号后,还需要能量检测器探测磁异信号,对探测到的信号进行平方求和,得到信号能量E,并将其与设定的能量阈值Em进行比较,以完成磁异信号检测[10]:
2.3 吸烟组、戒烟组及非吸烟组的椎体骨折阳性率比较 结果表明:吸烟组、戒烟组及非吸烟组的椎体骨折阳性率分别为23.3%(496/2 129)、21.8%(76/349)和14.2%(131/925),组间差异有统计学意义(P<0.05);经两两比较,发现吸烟组与非吸烟组(P<0.001)、戒烟组与非吸烟组(P=0.001)的差异均有统计学意义。

由式(4)可知,当E>Em时,表示探测系统检测到磁异信号;当E<=Em时,表示信号未达到设定能量阈值,无铁磁性物质磁场干扰。
2 EMD算法
经验模态分解法能将任何复杂的时间、空间信号分解为从高频到低频的若干阶固有模态函数(Intrinsic Mode function,IMF)[11],每个IMF 均为稳定的窄带信号,分别表征信号的具体特征,而分解成固有模态函数的限制条件包括整个数据段极值个数和零点个数相差不超过1,在任何数据点上包络(由局部极大值点形成)和下包络(由局部极小值点形成)的平均值为0,即上下包络局部对称[12]。EMD 算法基本计算流程如图3所示。

Fig.3 EMD algorithm flow chart图3 EMD算法流程图
由图3 可见,EMD 算法的基本计算流程可分为以下4个步骤:
步骤1:取原始信号S(t)的局部极大与极小值点,分别采取三次样条插值的方法构建S(t)的上包络Su(t)和下包络Sl(t)。
步骤2:平均处理上包络Su(t)和下包络Sl(t),获得平均值函数m(t),该值代表原始信号S(t)的低频成分,通过S(t)减去m(t)得到新数据序列h1(t)。
步骤3:利用IMF 评判标准判断h1(t)是否符合要求,若不符合,将h1(t)代入重复步骤1、步骤2,直至h1(t)达到IMF 标准,如此可得到表征S(t)最高频率组成部分的第1个IMF 分量x1(t)。
步骤4:首先利用原始信号S(t)减去x1(t)得到剩余分量r1(t)。


最后,当数据序列呈现单调特性或整个序列只存在一个极点的条件下,原始信号S(t)将终止分解。最终剩余分量即为EMD 分解所产生的残差分量Res(t),该分量代表原始信号的整体趋势。综上,EMD 将原始信号分解为若干个IMF 分量和残差分量,即可用式(7)表示原始信号S(t)。

EMD 是一种时间尺度分析方法,对原始信号进行EMD 分解所产生的若干IMF 分量,每个分量分别体现不同时间尺度特征,而该特征显示的是非平稳非线性信号的固有模态特征,因此需要选择合适的分解层次进行组合[13],保证信号完整性,过滤高频噪声信号,获取高信噪比目标信号。本文在图2 的磁异仿真信号上增加不同高斯噪声,组成信噪比分别为-5dB、-7dB、-10dB 复杂背景下的磁异仿真信号,并使用EMD 算法对上述仿真信号进行分解,获取不同的IMF 分量并对其进行筛选和重组[14],由于高频噪声信号往往在高阶IMF 分量中占比较高,因此在重组时将首先剔除高阶IMF 分量。其中,一阶、二阶IMF 分量中高频噪声占比较大,故可选择性地去除一、二、三阶IMF 分量[15],仿真结果如图4所示。
图4(a)、图4(c)、图4(e)分别为信噪比为-5dB、-7dB、-10dB 噪声干扰的磁异仿真信号,经过EMD 分解重构的数据波形分别如图4(b)、图4(d)、图4(f)所示。通过上述EMD 分解结果可知,对不同信噪比的磁异信号数据,EMD 均能较好地剔除高频噪声,提取磁异信号的准确性较高,得到的处理信号具有较高的信噪比和稳定性。但在实际探测环境中,由于MRI 受到强磁干扰、铁磁性目标物质体积材质不宜探测、人员体内植入铁磁性目标物质等因素,导致磁异信号被噪声信号覆盖。为了验证该算法的通用性和鲁棒性,本文将采用实测磁异信号数据对EMD 算法进行实验。

Fig.4 EMD decomposition and reconstruction results of different SNR simulation signals图4 不同SNR仿真信号的EMD分解重构结果
3 仿真实验
3.1 数据采集
本文实验数据由实验室自主设计的基于磁通门传感器的铁磁性物质探测系统收集,该系统通过ADC 模块将模拟磁异信号转化为数字信号,配置了蓝牙串口传输功能的上位机以显示和保存数据。数据采集地点为不同医院核磁共振室门外,以钳子、手机、钥匙和硬币共4 种常见的铁磁性物质被测目标。首先固定被测目标与探测系统的距离,测试探测系统在不同角度下的探测性能;然后固定被测目标与探测系统的角度,测试探测系统在不同距离的探测性能。
3.2 EMD算法验证
在测试实验中,为了避免复杂背景环境会给磁异信号与无关因素对检测造成干扰,采取控制变量法进行测试。同时,为避免实验数据量较大,本文仅以4 种被测物体在0°测试角度、120cm(钳子、手机的最远测试距离)和50cm(钥匙、硬币的最远测试距离)距离条件下进行测试,在MATLAB 中编写EMD 数据处理的算法模型,使用UDWT算法对数据进行滤波处理,处理结果如图5所示。

Fig.5 EMD processing results of the magnetic abnormal signals of four measured substances图5 4种被测物质磁异信号的EMD处理结果
图5(a)、图5(d)、图5(g)、图5(j)分别为钳子、手机、钥匙、硬币在MRI 室外复杂环境下由铁磁性探测系统探测的磁异信号波形,可明显看到信号存在较大噪声干扰。由于被测物体对磁场的影响程度不同,因此造成平均幅值依次降低。图5(b)、图5(e)、图5(h)、图5(k)分别为上述磁异信号经过EMD 处理过后重构的信号波形,图中圆圈部分波形为被测目标所产生的磁异信号。图5(c)、图5(f)、图5(i)、图5(l)分别为上述磁异信号经过UDWT 处理后的信号波形,经过UDWT 滤波后虽保留了信号的有效信息,但信号仍然存在毛刺。
通过比较可知,EMD 处理后的波形相较于UDWT 滤波后更平滑,在去除高频噪声信号的同时保留了原始信号的有效成分,保证了原始信号的完整性。由测试结果可知,EMD 算法相较于传统方法,处理不同测试物体的磁异信号更稳定,能有效过滤提取MRI 复杂背景环境下铁磁性物质的磁异信号。此外,本文采用信号信噪比SNR 作为数据处理效果衡量指标,并将EMD 方法与UDWT 方法所处理的结果进行比较,结果如图6-图7所示。

Fig.6 SNR of EMD processing signals图6 EMD处理信号的信噪比

Fig.7 SNR of UDWT processing signals图7 UDWT处理信号的信噪比
图6 中4 条折线分别代表4 种被测物体,横坐标为测试距离,纵坐标为信噪比。由此可见,磁异信号经过EMD处理过后的信噪比高达到16dB 以上,相较于原始信号具有较大提升。由图7 可见,UDWT 方法对磁异信号的滤波效果不佳,滤波后信号的信噪比处于8dB 以下,且当被测物体距离增加,磁异信号强度会随之减小,信噪比处于下降趋势。
综上所述,EMD 方法相较于UDWT 方法,去除高频噪声更高效,能大幅度提升信号信噪比,对磁异信号的探测效果良好。同时,该方法可提高探测距离与灵敏度,更好的保证信号完整性,为检测铁磁性目标物质提供良好的数据保证。
4 EMD方法改进
目前,EMD 方法存在模态混叠问题。模态混叠是指同一IMF 分量包含差异较大的特征时间尺度,或相近特征时间尺度分布在不同的IMF 分量中,该问题主要由于在分解的过程中局部极值在短时间内发生多次跳变所导致,将致使IMF 分量失去物理意义,影响后续时频分析处理。
为此,邹瑛珂等[16]提出协方差叠加经验模态分解(Covariance Superposition Empirical Mode Decomposition,CSEMD)的改进型EMD 方法,基本原理是加强信号中具有高相关性的信号,减少低相关性的信号(一般为噪音)。CSEMD 方法首先对原信号进行EMD 分解取得IMF 分量;然后对各IMF 分量和原信号进行协方差运算,将协方差标准化后进行排序,将最大值与最小值相减后取平均;最后在原信号基础上增加平均值进行EMD 分解得到高信噪比的IMF 分量。
本文实验测试数据共200 组,4 种被测铁磁性物质各50 组,由于磁异信号与探测角度、探测距离、被测物质的铁磁性成分占比相关,因此固定测量角度,依次增加测试距离进行实验。其中,钳子与手机的测试距离为10cm、30cm、50cm、80cm、120cm,钥匙与硬币的测试距离为10cm、20cm、30cm、40cm、50cm,每个均距离测试10次。
首先将实验数据分别进行CSEMD、EMD、UDWT 处理,然后通过能量检测器检测磁异信号。若无磁异信号时,能量检测器的输出较为平缓;当出现磁异信号时,检测器表现为能量波形凸起;若能量幅值超过设定能量阈值,则将触发光声报警。铁磁性物质检出率如表1所示。
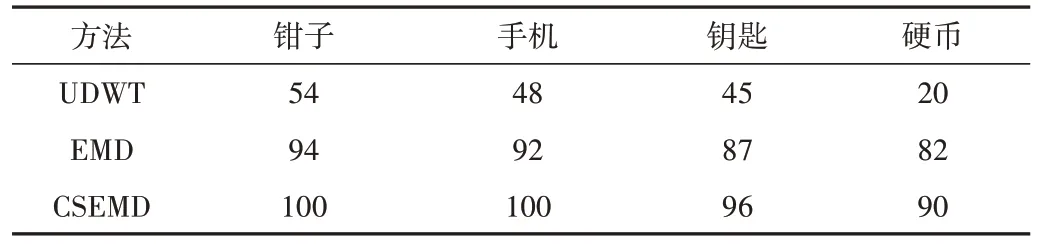
Table 1 Detection rate of different ferromagnetic substances by three methods表1 3种方法对不同铁磁性物质的检测率 (%)
由表1 可知,UDWT 方法对于磁异信号的检测效率较低,并且随着铁磁性物质含铁磁量减小而降低,无法有效检测被测铁磁性物体;EMD 方法在磁异信号的检测方面明显优于UDWT 方法,大幅度提升了检测铁磁性物质的准确率;CSEMD 方法在EMD 的基础上对模态混叠问题有所抑制,提高了磁异信号的检测效率。
5 结语
本文提出无需任何先验信息且适用于非平稳、非线性信号的EMD 算法,并将该算法应用于MRI 室外强磁环境中检测微弱的磁异信号。首先对包含高频噪声的磁异信号进行EMD 分解,剔除含有高频噪声的IMF 分量再重构其他分量以保证信号的完整性;然后使用改进型CSEMD 方法抑制EMD 方法模态混叠问题;最后通过能量检测器检测磁异信号,提高EMD 方法对铁磁性物体检测准确率。
实验数据表明,EMD 算法将磁异信号波形的信噪比提高至16dB 以上,相较于传统的UDWT 算法提高了8dB 以上。同时,使用改进EMD 方法检测磁性物质的准确率高达90%以上,能有效检测MRI 复杂环境背景下微弱的磁异信号,显著提高了铁磁性探测系统的检测距离和检测效率。然而,本文仅将该方法运用于MRI 领域,下一步将在不同领域测试算法的适用性。
