改进未知互耦信息下矩阵重构算法的波束形成

谢 宇，黄 鹏，李 震，李良荣*

(1.贵州大学 大数据与信息工程学院，贵州 贵阳 550025；2.北京航空航天大学 电子信息工程学院，北京 100083)

0 引言

波束形成的实质是接收期望信号的同时抑制内部的干扰和噪声[1-3]。但在实际应用中，总有各种不确定因素影响导致波束形成器的性能下降。如导向矢量存在误差[4-6]、期望信号来波方向失配等。Gershman等人提出了最差情况性能最优(Worst-Case Performance Optimization，WCPO)算法[7]解决了导向矢量的误差情况，该算法在不确定集约束的范围内，让所有导向矢量的波束响应均大于等于1的前提下，求取满足目标函数的最优权矢量。针对导向矢量失配问题，Gu等人[8]于2012年提出干扰加噪声协方差(Inter-ference Plus Noise Covariance，INC)矩阵重构的算法，为了收集干扰信息，首先在不含有期望信号的角度区间上积分，然后通过求解二次约束等问题估计期望信号的方向矢量失配量，能够有效抑制噪声。

上述算法虽然在改善波束形成器性能方面能达到较好的效果，但是在面对阵列互耦时却不能很好地抑制干扰。互耦的存在导致数据矩阵结构改变，使得传统波束形成器输出效果变差。因此，陆续有学者提出了改善此问题的办法。Huang等人[9]提出一种基于迭代思想的最优化二次约束问题来同时估计信号DOA以及互耦矩阵的互耦系数，利用Capon空间功率谱得到针对阵元互耦情况时的波束形成器，能有效校正阵元互耦现象。文献[10]提出了先估计互耦系数，再重构INC矩阵的抗互耦算法。而未知互耦信息下的波束形成算法不需要预先估计互耦系数，可利用最大化输出信干噪比准则求出权向量。文献[11]提出的基于未知互耦信息下矩阵重构的算法，利用协方差矩阵锥化理论(Covariance Matrix Taper，CMT)和空间功率谱采样重构包含互耦信息的INC矩阵，并对其进行特征分解，经过计算得到最优权矢量。该算法在高信噪比时抗互耦性能较好，但在低信噪比下，不能有效抑制干扰和噪声，使得波束形成器性能下降。

本文研究一种基于未知互耦信息下矩阵重构的算法(Matrix Reconstruction with Unknown Mutual Coupling Information，MUMC)，并在此算法基础上进行改进。原算法解决了互耦信息未知的矩阵重构，但是没有考虑到低信噪比(Signal Noise Ratio,SNR)下导向矢量损耗的情况，导致波束形成输出不稳定。针对原算法在低输入信噪比下干扰方向不能准确地形成零陷[12]，且波束形成器不够稳健的问题，本算法首先通过计算在不含有互耦信息的期望信号导向矢量上适配一个误差值，以减消低信噪比下矩阵重构和特征分解对导向矢量的损耗，然后设定一个输入信噪比的门限，针对不同信噪比输出不同的导向矢量值，目的是将导向矢量准确输出得到平稳的计算结果。仿真实验证明不论在高信噪比还是低信噪比下，该波束形成器都能稳健输出。

1 算法原理

1.1 算法模型

假设阵列形式为M元半波长等间距的均匀直线阵[13-14]，所有信号都是窄带信号。当存在互耦[15]时，θ方向的导向矢量经过转换可建模为：

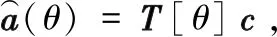
(1)

式中，T[θ]=T1(θ)+T2(θ)为一个M×Q的矩阵[14]。T1(θ)和T2(θ)表示为：

(2)

(3)

则存在互耦时的阵列接收信号矩阵可写为：

(4)

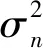
接收信号的协方差矩阵为:

(5)

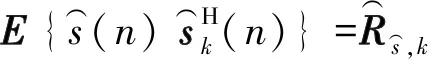
(6)

对式(6)进行优化问题的构造求解，即得到存在互耦时的自相关矩阵以及接收信号复包络的估计值，可估计出存在互耦时的INC矩阵。

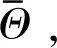
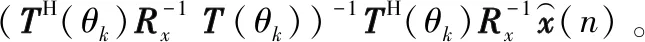
(7)

由于干扰的真实数量少于潜在干扰的数量，为了让潜在信号的功率达到干扰所在的位置，限定一个范围，对估计功率进行升序排序，使得能到达一定水平的潜在信号的功率筛选通过。因此，潜在信号的功率估计为：

(8)

式中，trace[·]代表矩阵的迹[15]。

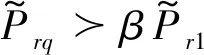
(9)

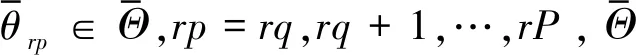
(10)

利用存在阵列互耦信息的接收信号表达式(4)，让其通过子空间D后，可求得只包含期望信号和噪声信息的接收信号y(n)：

DZa(θ0)s0(n)+De(n)=a′(θ0)s0(n)+De(n),

(11)

式中，n=1,2,…,N。

因为实际中无法计算真实的接收信号自相关矩阵，则用y(n)的样本协方差矩阵取代：

(12)

式中，N为样本数目。

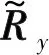
(13)

滤波器输出为：

(14)

则最优权矢量为：

(15)

通过上述步骤，在存在未知阵元互耦时的信号模型中仅需要估计出接收信号复包络及其协方差矩阵，再选择功率较大的角度进行干扰加噪声协方差矩阵的重构，在对INC矩阵和接收信号自相关矩阵进行特征分解后，经过计算得到最优波束形成。

1.2 原算法仿真

对上述算法的性能进行Matlab仿真实现。仿真环境为：具有互耦存在的16元阵元数的均匀线阵，入射信号有3个，其中两个是干扰方向信号，入射角度设置为-30°和+30°；另一个是期望信号，角度设置为0°，将输入信噪比设置成20 dB，干噪比设置成30 dB，信号采样点数200，互耦门限为5，则互耦向量设定为：[1，0.512 8+0.387 5j,0.355 8+0.278 5j,0.363 6-0.363 6j,0.102 4+0.052 1j],图1为算法的归一化波束图仿真。

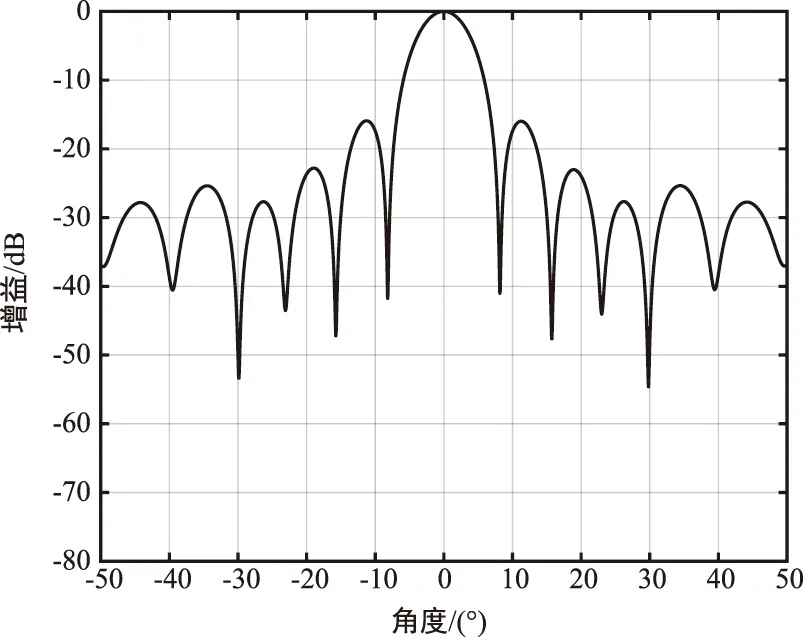
图1 基于未知互耦信息的矩阵重构算法的归一化波束图Fig.1 Normalized beam diagram of matrix reconstruction algorithm based on unknown mutual coupling information

从图1可以看出，该算法能准确地在期望来波方向上形成主波束，并在两个干扰角度-30°和30°上都形成了零陷，说明该算法具有一定的抗互耦作用。但是两边的零陷深度较浅，未超过-55 dB，说明互耦信息的影响较大，当噪声等干扰信息方向有偏差时,则算法性能将会下降。

2 改进算法

2.1 原算法存在问题

在对如上算法的分析中可以得知，在高信噪比和高干扰输入功率下，原算法在对抗阵元互耦上不需要预先估计互耦系数，只需利用最大化输出信干噪比准则对权向量进行求解。无论期望信号功率增强还是减弱都保持了很好的性能。但是当输入信噪比较低时，原算法对干扰的抑制能力明显下降，且不能在干扰方向形成准确的零陷，整个算法性能失衡。图2为原算法在-20 dB信噪比输入下的波束形成图。

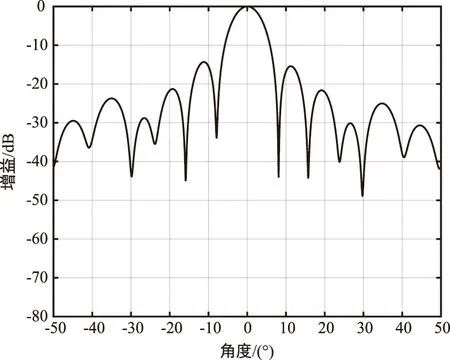
图2 低输入信噪比之下波束形成归一化方向图Fig.2 Normalized pattern of beamforming under low input SNR

如图2所示，原算法实验一旦进入较低的信噪比环境时其抗干扰能力变差，在两个干扰角度未形成明显的零陷，且并没有减弱因阵元互耦带来的影响，意味着在低信噪比下该算法的性能仍有需要改进的空间。

2.2 算法改进

阵列间互耦的存在使得干扰零陷抬高、波束形成的主瓣偏移等，这严重影响了波束形成器的性能。在经过多次试验仿真发现，原算法在信噪比大于10 dB时表现良好。因此，只需要设定一个条件在低于此环境时适配精确的导向矢量，使得优化后的矢量不被阵元间的互耦所干扰，能够抵抗因低输入信号而带来的不同程度噪声的干扰。

已知阵元上的接收信号可表示为：

(16)

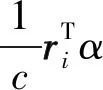
因为阵列信号一般都是转变到基带再进行处理，所以可将其用矢量形式表示为：

s(t)≜[s1(t),s2(t),…,sM(t)]T=

(17)

当确定了波长和阵列的结构时，式(17)中的矢量部分只与到达波的空间角矢量θ有关，称为方向矢量：

(18)

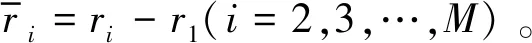
因为阵列间互耦的存在将不同位置的阵元所处的电磁环境改变，加上输入信号中携带的噪声过杂，在低信噪比下将会损耗方向矢量，令误差产生。因此，为了降低噪声对转换过程的消耗，经过不断地实验计算，最终确定在建立互耦信息前的方向矢量上赋予一个误差值，可增加互耦之后的导向矢量准确性：

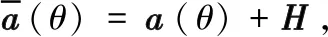
(19)

其导向矢量矩阵为：

(20)

计算时，若是在存在互耦信息的导向矢量上赋予误差，则互耦与误差将会产生混淆，导致抗互耦效果变差，因此要在这之前就给导向矢量适配误差。加入误差之后，在导向矢量的左侧再乘上互耦矩阵，则存在互耦时的导向矢量为：

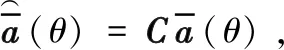
(21)

对应的导向矢量矩阵为：

(22)

式中，C为反映互耦影响程度的互耦矩阵MCM。因为C为Toeplitz矩阵，则经过推导可以得到：

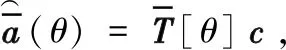
(23)

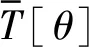
(24)

进行到这一步，对导向矢量的误差适配就基本完成了。接下来，需要对算法当前信噪比环境进行一个门限判断。如果当前信噪比环境大于或等于10 dB，则算法继续，如果当前信噪比低于10 dB，说明算法此时处于一个低信噪比环境下，则需要在导向矢量上增加一个误差值，保证算法能够稳健输出。部分算法流程如图3所示。

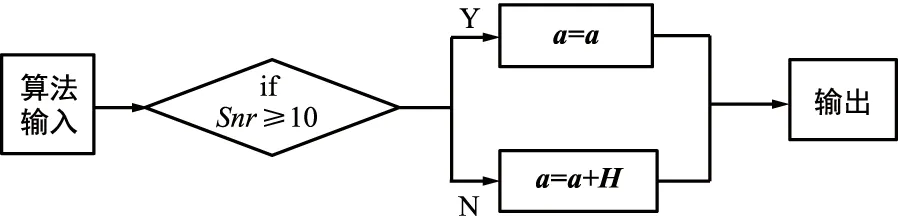
图3 部分算法流程图Fig.3 Partial algorithm flowchart

另外，设定信噪比门限为了防止在高信噪比时加入的导向矢量误差影响到算法运算，造成方向图输出不准确。因此，在低于10 dB的信噪比下给导向矢量适配误差，使得算法无论在高信噪比还是低信噪比下都能够保证算法稳定输出。

3 仿真实验

3.1 改进算法仿真

通过仿真验证改进算法的性能，假设期望信号来波方向为0°，同时加入两个干扰方向为[-30°,30°]，干噪比设为30 dB，输入端SNR设为-20 dB，互耦系数设置为[1，0.512 8+0.387 5j,0.355 8+0.278 5j,0.363 6-0.363 6j,0.102 4+0.052 1j]，图4为改进算法仿真得出的归一化方向图。

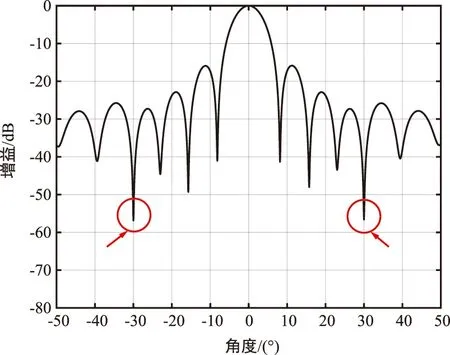
图4 低信噪比情况下改进算法的波束归一化方向图Fig.4 Beam normalization pattern of the improved algorithm in the case of low SNR

可以看到，图2的仿真与图4的仿真区别在于对干扰的抑制能力以及波束输出的稳健性。图4仿真的波束图，其主瓣对准了真实的期望信号来波方向，在干扰方向零陷深度均超过-55 dB，且界限清晰波达方向明确，很好地说明了算法的有效性。

3.2 综合仿真对比

为了更加清晰地对比改进算法与其他算法的性能，将本算法与其他算法放置在同一环境中进行仿真验证。

对比的算法：改进前的Yang算法、SMI算法、基于互耦系数估计的抗互耦算法(Mutual Coupling Coefficient Estimate Based，MCCEB)、常规ESB算法。

综合仿真：设置输入信噪比为-20 dB，干噪比设为30 dB，期望信号估计来波方向为0°，两个干扰信号的真实来波方向分别为-30°和30°，快拍数L=200。

由图5可以看出，在波达方向为0°的情况下，本文算法(记为IMPROVE)假设的来波方向与实际的来波方向完全一致，在所对比算法中对干扰的指向也是最准确的。Yang的算法在低信噪比下波束赋形不稳定。ESB算法对干扰抑制混乱，在其他角度形成了零陷，与设定的仿真环境不符。而SMI算法则是将期望来波信号当成了干扰抑制，出现了信号自消的现象。MCCEB算法是主要针对抗互耦的算法，但是在仿真图中可以看到，它在未知互耦条件下对干扰的抑制能力尚欠缺。综合来看，本文算法在低信噪比的环境中表现是很突出的。

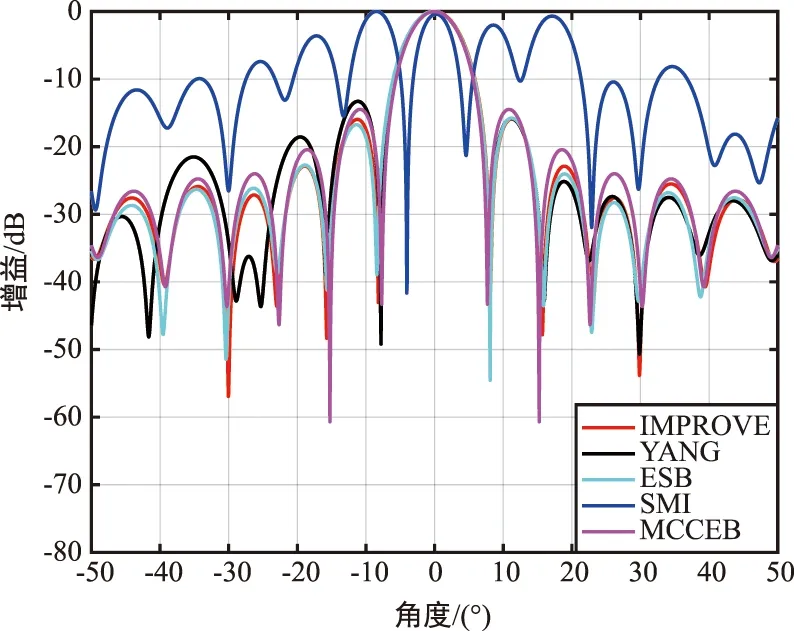
图5 各种算法在互耦情况下的方向图对比Fig.5 Direction diagram comparison of various algorithms in the case of mutual coupling

4 结束语

本文针对基于未知互耦信息下矩阵重构算法存在的问题，即在低输入信噪比下，波束形成器输出结果不理想，抗干扰效果不明显。对此现象进行分析，并对算法改进，当输入SNR低于10 dB时，在期望信号的导向矢量上补充一个误差值，使得后续重构干扰加协方差矩阵以及进行二次特征分解时含有的部分期望信号导向矢量消耗得以补偿，当输入SNR大于10 dB时，则按照原算法计算思路进行未知互耦信息下的波束输出。通过理论剖析和仿真实验对比，验证了该算法提高低信噪比下的抗互耦性能，无论在高信噪比还是低信噪比下都能良好运行，在解决未知互耦信息的耦算法中，该算法具有较强的实用性及稳健性。而对于来波信号靠近时，干扰的进一步准确识别是下一阶段需要解决的问题。