无人机虚拟天线阵列安全节能通信多目标优化

李洪娟，潘雯敬，李家辉，孙 庚*

(1.吉林大学 软件学院，吉林 长春 130012；2.吉林大学 计算机科学与技术学院，吉林 长春 130012)

0 引言

由于其高机动性、较广的覆盖范围和部署的灵活性，无人机(Unmanned Aerial Vehicle，UAV)被广泛应用于各领域[1]。近年来，基于无人机的无线通信和网络受到愈来愈多的关注[2]，例如，无人机可以部署为空中基站，为地面用户(Ground Users，GUs)提供高效、低成本的网络服务[3]。又如，无人机可以作为新的空中用户，在空中接入蜂窝网络加入通信[4]。再如，无人机也可以用于物联网通信，在分布广泛的无线设备之间完成数据收集、传播等任务[5]。然而，由于无线信道的广播特性以及无人机和地面用户之间的视距(Line-of-Sight，LoS)信道特点，安全性和保密性问题成为无人机通信中一个具有挑战性的问题[6-7]。

在无线通信中，上层加密是实现保密通信的常用方案，但这种方法对设备的计算能力要求较高，因此并不适用于硬件资源有限的无人机网络。物理层安全(Physical Layer Secure，PLS)是实现安全通信的另一种有效方案，该技术利用信道特性向未经授权的接收者隐藏信息，不需要复杂的加密解密操作，因此，PLS是解决无人机安全通信的有效手段。例如，文献[8]根据无人机具有高机动性的特点，通过联合优化无人机的轨迹和在有限范围内的传输功率，以最大化无人机通信系统的保密率。再如，Wen等人[9]通过联合优化无人机轨迹、发射功率和用户调度，以最大化无人机到所有地面用户之间的最小平均保密率。然而，传统的基于无人机的PLS方法往往需要无人机飞行至目标接收者周围实施PLS策略，该过程将极大增加无人机的推进能耗。

协作波束成形(Collaborative Beamforming，CB)是在无人机通信中实现PLS策略的一种可行方法。具体而言，多个无人机组成一个基于无人机虚拟天线阵列(UAV-enabled Virtual Antenna Array，UVAA)，其发射的电磁波在传播过程中发生叠加和偏移，从而形成具有高增益主瓣和低信号强度的旁瓣波束方向图，通过将主瓣指向目标接收者和旁瓣指向窃听者可以有效提高传输距离和保密效果。例如，Zhu等人[10]制定了一个无人机位置、模拟波束成形和功率控制联合优化问题，以最大化从源节点到目标节点的可实现速率。Mohanti等人[11]设计了一种分布式空对地波束成形方法，即AirBeam，该方法在满足地面接收者服务质量要求的同时，实现了高度定向传输。然而，无人机通常是随机分布的，这将降低UVAA的性能。在这种情况下，无人机可以被分配更优的CB位置，但这无疑会增加无人机的推进能耗。此外，无人机天线用于CB的激励电流权重也会直接影响UVAA的性能。因此，亟需一种优化方法来确定无人机的最优位置以及激励电流权重来通过CB实现安全且能量有效的通信。

基于上述考虑，本文构建了一个安全和能量最小化通信多目标优化问题(Secure and Energy Minimization Communication Multi-objective Optimization Problem，SEMCMOP)，以同时最大化UVAA对多个地面用户的总保密率，并降低无人机的总推进能耗。此外，本文使用多目标粒子群优化算法(Multi-objective Particle Swarm Optimization，MOPSO)求解SEMCMOP并进行相关仿真实验。

1 系统模型和问题构建

本章首先介绍所使用的系统模型，然后基于上述模型构建SEMCMOP。

1.1 系统模型

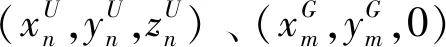
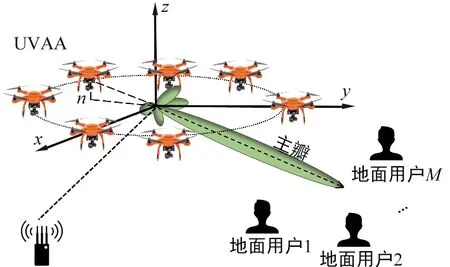
图1 无人机虚拟天线阵列通信系统Fig.1 UAV-enabled virtual antenna array communication system

1.1.1 基于UAVV的阵列因子模型

在UVAA中，无人机的位置和用于CB的激励电流权重会影响阵列因子(Array Factor，AF)的辐射分布，ωn表示UAVV中第n个无人机的激励电流权重，根据电磁波叠加原理，AF可以建模为[12]：

(1)

式中，θ∈[0,π]和φ∈[-π,π]分别表示仰角和方位角，k=2π/λ为相位常量,λ为信号波长。

1.1.2 无人机保密率模型

本文使用LoS信道模型，UAVV与第m个地面用户通信时，第m个地面用户所在方向的增益为[13]：

(2)

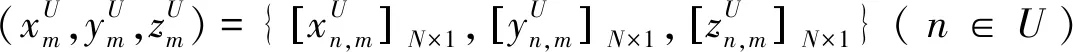
同理，UAVV与第m个地面用户通信时，窃听节点所在方向的增益为：

(3)

在不考虑窃听节点的情况下，UAVV到第m个地面用户的通信速率可以表示为[14]：

(4)

式中，B为传输带宽，dGUm表示UAVV原点与第m个地面用户之间的距离，KGUm为无人机与第m个地面用户之间的恒定路径损耗系数，Pt为无人机的总发射功率。相似地，UAVV到窃听节点的通信速率可以表示为：

(5)

式中，dEN表示UAVV原点与窃听节点之间的距离，KEN表示无人机与窃听节点之间恒定的路径损耗系数。

当UAVV向第m个地面用户发送一些机密信息时，系统中的窃听节点会截获UAVV发送的信息。当UAVV与第m个地面用户的通信速率RGUm一定时，UAVV与窃听节点之间的通信速率REN越小，窃听节点窃听到机密信息的概率越小。因此，UAVV与第m个地面用户通信时保密率CGUm可以表示为：

CGUm=RGUm-REN=

(6)

1.1.3 无人机能量损耗模型

在文献[15]中，无人机的能量损耗主要分为通信能耗和推进能耗两部分。一般来说，无人机的推进能耗远超通信能耗，因此与通信相关的能耗可忽略不计。

旋翼无人机在二维(Two Dimensional，2D)平面飞行时的推进能耗可以表示为[15]：

(7)

式中，v表示无人机的速度，其他参数可视为与无人机相关的常数。根据文献[15]，本文合理地忽略无人机水平飞行时由于加速或减速引起的额外的能量损耗。

此外，无人机在形成UAVV过程中会产生上升和下降的3D轨迹，3D无人机轨迹的推进能耗为[16]：

(8)

式中，v(t)和T分别表示无人机在t时刻的瞬时速度以及无人机结束飞行的时间，mU和h分别为无人机的机体质量和高度变化，g为重力加速度。

1.2 问题构建

本文所考虑的基于无人机的通信系统中无人机与地面用户相距遥远，因此，当无人机需要发送数据给地面用户时，这些无人机会组成一个UAVV并使用CB向地面用户传输数据。

然而，由于UAVV与地面用户通信时存在窃听节点对传输数据进行拦截，因此安全性和保密性问题必须引起重视。可以考虑通过改进UAVV的性能从而使窃听节点无法获得足够的通信速率。具体而言，通过确定无人机的最优位置和最佳激励电流权重来生成具有高增益主瓣和低信号强度旁瓣的波束图，将主瓣对准合法的地面用户而被抑制的旁瓣指向窃听节点，从而降低UAVV到窃听节点的传输速率。然而，无人机在形成UAVV过程中必然会产生额外的推进能耗，从而降低无人机网络的寿命。因此这两个条件之间是互相权衡的，需要综合考虑。

本文假设无人机需要将收集到的数据传递给所有地面用户。然而，UAVV的主瓣每次只能指向一个地面用户，这意味着UAVV每次与地面用户传输完成后需要重新定位。因此需要考虑UAVV与每个地面用户的通信顺序，因为UAVV与地面用户的通信顺序会影响无人机的推进能耗。因此，优化目标详述如下。

优化目标1为解决在存在窃听节点的情况下无人机与地面用户安全通信的问题，无人机需要组成UAVV与不同的地面用户通信，本文首先最大化UAVV与所有地面用户通信的总保密率，表示为：

(9)

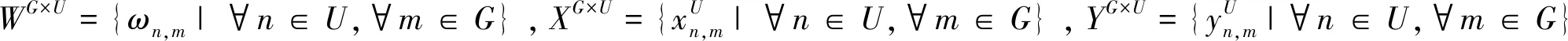
优化目标2为实现第一个优化目标，无人机需要飞到更好的位置形成UAVV与不同的地面用户通信，这会增加无人机的推进能耗，为减少无人机形成UAVV过程中的总推进能耗，第二个目标函数可以表示为：

(10)

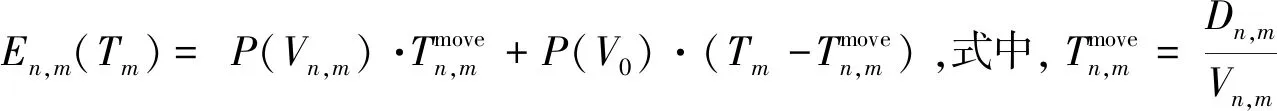
因此，基于UAVV实现的安全节能通信多目标优化方法可以表示为：

(11a)

s.t. 0≤ωn,m≤1,∀n∈U,∀m∈G，

(11b)

(11c)

QG×1∈，

(11d)

D(n1,n2)≥Dmin,∀n1,n2∈U，

(11e)

本文构建的SEMCMOP是一个NP难问题，为了便于分析且不失一般性，本文对f2进行简化并通过证明简化后的f2是一个NP难问题,从而证明SEMCMOP是一个NP难问题。

假设组成UAVV的无人机位置和激励电流权重固定且已知，f2和相应的约束条件如下：

(12a)

s.t.QG×1∈，

(12b)

式中，Eqm,qm+1表示N个无人机从与第qm个地面用户通信到与第qm+1个地面用户通信的总推进能耗，可以看出简化后的f2实际上是一个旅行商问题(Traveling Salesman Problem，TSP)[14,18]，而TSP已被证明是NP难问题。由于f2是一个NP难问题，因此SEMCMOP是一个NP难问题。

2 求解方法

本章首先介绍多目标优化问题的相关概念，然后引入MOPSO算法来解决本文提出的多目标优化问题(Multi-objective Optimization Problems，MOP)。

2.1 多目标优化问题

本节简要地介绍MOP中一些重要的概念[19]。

多目标优化模型MOP是涉及多个目标函数同时优化的问题，其主要目标是找到满足约束条件的最小化向量函数的决策变量X=(x1,x2,…,xd)，MOP可以建模为：

F(X)=(f1(X),f2(X),…,fM(X))T，

(13)

式中，fi(X)表示第i个目标函数，M为目标函数的总数。

帕累托支配对于任意两个解X，X′∈Ω，对应的目标函数值为F(X)、F(X′)。如果X支配X′并记为XX′，则有：

(14)

帕累托最优如果在整个决策变量空间内不存在任何决策变量支配X*，则称决策变量X*∈Ω是帕累托最优的。

帕累托最优集在MOP中，对于给定的一组最优解，如果解集中的解都是非支配解，也就是说，解集中的解彼此互不支配，则该解集称为帕累托最优集。

帕累托前沿帕累托最优集中的每个解相对应的目标函数值构成的向量集称为帕累托前沿。

2.2 粒子群优化算法

粒子群优化(Particle Swarm Optimization，PSO)算法是一种群体智能(Swarm Intelligence，SI)算法，主要通过群体中个体之间的协作和信息共享来寻找最优解[20]。具体而言，在PSO中每个解想象为搜索空间中的一只鸟，称为“粒子”，每个粒子有两个属性：速度v和位置x，前者表示移动的快慢，后者代表移动的方向。每个粒子在搜索空间中独立搜索最优解，并将其记为当前个体极值(pbest)，粒子之间通过信息共享，找到所有粒子个体极值中最优的那个值记为全局极值(gbest)。在每次迭代中，粒子根据pbest和gbest来调整自己的速度和位置，具体方式如下：

vi=ω×vi+c1×rand()×(pbesti-xi)+

c2×rand()×(gbestg-xi)，

(15)

xi=xi+vi，

(16)

式中，vi和xi分别表示第i个粒子的速度和当前位置，ω表示惯性因子，是一个非负值，rand()是介于(0,1)之间的随机数，c1和c2是学习因子。

2.3 MOPSO算法

本节首先介绍MOPSO算法，然后给出MOPSO解决SEMCMOP的主要步骤以及相关分析。

2.3.1 算法简介

MOPSO算法是PSO算法的一种扩展，在解决多目标优化问题方面有强大的性能[21]。具体而言，MOPSO算法首先通过随机的方式生成一组粒子(解)，然后在每次迭代中通过式(15)～(16)更新每个粒子的速度和位置，直到找到满足终止条件的帕累托最优集。相较于PSO算法，MOPSO算法通过引入存档和自适应网格法以解决多目标优化问题。

存档是一个全局存储库，存储着每一次迭代产生的帕累托最优解。最初存档为空，随着不断的迭代，每一次迭代产生的帕累托最优解Snew会更新存档，存档的更新机制如下：

①Snew被存档中的解支配，则直接将Snew丢弃；

②Snew和存档中的解互不支配，则将Snew加入到存档中；

③Snew会支配存档中的一些解，则将这些解移出存档并将Snew加入到存档中；

④ 当存档已满时，根据自适应网格法删除存档中的部分解并将Snew加入到存档中。

自适应网格法通过自适应网格法会将整个目标空间划分成多个网格，然后计算存档中每个粒子的网格编号，由此可以计算每个粒子的拥挤度，也就可以得到每个网格中帕累托最优解的密度。

MOPSO中pbest和gbest的更新方法如下：

①pbest的更新：当粒子通过位置更新公式得到一个新位置xnew后，需要通过帕累托支配来比较xnew与pbest的优劣，从而更新pbest；然而，xnew和pbest可能互不支配，在这种情况，本文将随机选择其中一个值作为pbest。

②gbest的更新：gbest需要从在存档中获取，首先根据自适应网格法计算出每个网格中帕累托最优解的密度，然后使用轮盘赌机制在密度最小的网格中选择一个解作为gbest。

2.3.2 MOPSO的主要步骤和分析

MOPSO的伪代码如算法1所示。在MOPSO中，首先通过随机的方式初始化一组粒子P，使用适应度函数评估每个粒子的值，将每个粒子的pbest初始化为其本身，根据存档A中粒子的拥挤度信息初始化gbest。在每次迭代中，对粒子的速度和位置进行更新，然后重新计算每个粒子适应度，根据适应度更新存档A、每个粒子的pbest以及gbest，直到收敛或达到最大迭代次数则退出算法。MOPSO使用自适应网格法更新gbest，即需要在存档中根据拥挤度大小更新gbest，拥挤度越小，该粒子被选择的概率越大，反之越小。MOPSO的计算复杂度主要在于目标函数和拥挤度的计算，当Nobj表示优化目标数时，目标函数的计算复杂度为O(Nobj·Npop)。而拥挤度的计算成本主要在于需要对存档中的解进行排序，为O(Nobj·NArc·logNArc)，其中NArc表示存档的大小。本文将存档A的大小设置为Npop，因此MOPSO的复杂度为O(Nobj·Npop2)。

算法1 MOPSO算法Input:粒子群P,粒子群总数Npop,最大迭代次数tmax,存档A等。Output:帕累托最优集。1.Initial:P为空,A为空。2.fori=1toNpop:3.以随机的方式初始化粒子Xi的位置xi,速度vi初始化为0;4.将粒子Xi(xi,vi)加入到粒子群P;5.初始化粒子Xi的个体极值pbesti=xi;6.end7.使用帕累托支配比较P中的粒子,将其中表示非支配向量的粒子的位置xnon存储到A中。8.fort=1totmax:9.根据式(15)更新每个粒子的速度;10.根据式(16)更新每个粒子的位置;11.更新A;12.更新每个粒子的pbesti;13.end

3 仿真结果与分析

本文使用Matlab进行仿真，其中路径损耗系数α、每个无人机的发射功率Pm和载波频率fc分别设置为2,0.1 W和2.4 GHz。此外，无人机和地面用户的数量分别设置为16和8。其他关键参数参考文献[13,15]。

表1显示了使用MOPSO方法在总保密率(目标1)和无人机的总推进能耗(目标2)方面获得的数值结果。可以看出，与未进行优化的情况相比，MOPSO在两个优化目标上获得了更优的结果。图2显示了无人机与第1个地面用户通信时在飞行路径方面的优化结果。可见，无人机的位置相较初始位置分布的更加紧密，更加适合进行无人机CB任务。此外，图3显示了通过MOPSO算法获得的解分布情况，可以看出通过MOPSO算法求得的解分布较为均匀，表明MOPSO可以有效地解决SEMCMOP问题。

表1 使用MOPSO算法获得的数值优化结果Tab.1 Numerical optimization results obtained by MOPSO

图2 无人机飞行路径Fig.2 Flight paths of UAVs

图3 使用MOPSO算法获得的解分布情况Fig.3 Solution distributions obtained by MOPSO

4 结论

本文研究了基于UAVV的安全节能通信问题。在所考虑的场景中，存在一个位置已知的窃听节点，其会对无人机与地面用户之间的通信进行窃听，因此多个无人机组成UAVV与地面用户通信以提高通信保密率。本文构建了SEMCMOP，以提高总保密率和降低无人机的总推进能耗，并证明了SEMCMOP是一个NP难问题。此外，本文使用MOSPO算法对SEMCMOP进行求解，仿真结果表明MOPSO可以有效地解决SEMCMOP问题。