基于等积环形分割的高频元件快速识别算法

尹可鑫，欧 阳，李柏林，林冬婷

（1.西南交通大学牵引动力国家重点实验室，四川 成都 610031；2.西南交通大学机械工程学院，四川 成都 610031）

1 引言

高频元件的智能精密加工工序流程中采用射频芯片技术，即将高频元件的加工工艺参数、电性能参数等信息载入射频芯片中，并与该元件所放置的托盘进行关联。由于在元件的热处理阶段，元件与托盘脱离导致元件原有的射频芯片失效，无法完成后续的智能加工所以需要对元件二次匹配识别。传统的元件识别方法是依靠人工完成，存在检测速度慢、主观性强、误检率高等缺陷。因此需要在热处理前后使用图像识别技术识别工件图像，完成元件信息的关联，实现整个加工过程的智能化。

针对图像识别技术，国内外学者提出了一些相关算法，主要可分为优化特征提取算法及优化特征匹配算法。文献针对多尺度[1−3]、大仿射、大规模复杂场景等不同的适应条件进行改进，但无法区分具有纹理复杂的工件。文献[4]提取图像中各设备的SIFT特征，并与标准库中的设备图像进行对比实现目标识别，由于该方法需要手动标注，因此难以应用于大批量的工件生产中。文献[5]通过计算文献[6]获取图像多个矩的互相关性以确定配准点位置，该方法虽然具有旋转及尺度不变性，但针对相似度较高的高频元件，识别能力较弱。此外，扩展的圆投影算法或者改进环投影向量模板匹配算法[7−8]由于使用像素平均值作为评判依据，导致高频元件的细节特征丢失。

针对上述算法应用于高频元件图像识别存在的问题，提出了一种基于等积环形分割特征的图像识别算法。首先使用滑动窗口的方法根据互信息熵快速定位，再利用等积环形对图像进行分割，通过计算各个环上的梯度幅值及方向得到匹配系数MRR，由此对不同的高频元件进行定位及识别。

2 图像识别算法

以精密加工的高频工件为研究对象，提出基于等积环形分割特征的图像识别算法，其整体框架流程，如图1所示。

图1 算法整体框架流程Fig.1 Overall Framework Flow of Algorithm

2.1 基于互信息熵的图像快速定位

由于互信息熵使用的是图像相关性的统计特征，因此具有旋转不变性。待检测图像与不同模板的定位结果，如图2所示。

图2 待检测图像与不同模板的定位结果Fig.2 Positioning Results of the Image to be Detected and Different Templates

根据图2所示，虽然互信息熵法根据图像本身的灰度值及形状信息来对其进行定位的准确度较高，对图像的水平、垂直、旋转变化的鲁棒性较好，但是对于相似度极大的精密加工高频元件，不能直接通过最大互信息熵I进行区分。因此，互信息熵法只能用于快速定位，在定位后的所有互信息熵点集结果中，选择互信息熵最大的n2个点作为待检测角点集。并且根据图像大小选择不同数目的待检测角点n2，其计算方式如下：

其中，cols及rows为图像的长、宽，得出的n2个滑动窗口的左上角点的点集分布图，如图3中黑色区域所示。

图3 互信息熵点集分布Fig.3 Distribution of Mutual Information Entropy Point Set

2.2 等积环形图像分割

图4 目标图像等积环分割结果Fig.4 Segmentation Results of Target Image with Equal Product Ring

2.3 匹配系数MRR的推导

2.3.1 Sobel算子的改进

Sobel算子是考虑了±0°、±90°4个方向的梯度加权求和的3×3各向异性的梯度算子。而待检测图像的内部加工纹理较为复杂且相对密集，传统的Sobel算子只描述了水平、垂直方向的特征并不能很好地描述其斜方向的细节特征，因此增加±45°以及±135°四个方向的卷积核。改进后的Sobel算子卷积核，如图5所示。卷积效果对比，如图6所示。可见加上±45°以及±135°卷积核后，对于斜方向的加工纹理表达能力更强，在原4方向卷积效果的基础上，添加更多有效描述。

图5 改进后的Sobel算子8方向卷积核Fig.5 Improved 8−Direction Convolution Kernel of Sobel Operator

图6 卷积核卷积结果对比Fig.6 Comparison of Convolution Results of Convolution Kernel

2.3.2 计算等积环的梯度幅值与梯度方向

在各个等积环中使用8方向Sobel算子计算梯度幅值（Pixel Gradient Amplitude，PGA）与梯度方向（Pixel Gradient Direction，PGD）的步骤如下：

（1）计算各方向的梯度幅值。设原图M为f(x,y)，0°方向卷积结果为T0，45°方向卷积结果为T45，90°方向卷积结果为T90，

PGA与PGD的整体计算流程，如图7所示。

图7 计算流程Fig.7 Calculation Flow

2.3.3 有效特征点的筛选

将上述所得到的梯度幅值PGA与梯度方向PGD分别进行统计分组，使用预先设置的阈值筛选出符合条件的有效特征。

（1）利用梯度幅值筛选每个圆环中的有效特征点。图8（b）为图8（a）的梯度幅值3维分布图。由于模板是由程序自动分割，在模板的4个边界不可避免的出现部分背景区域也因此导致了图8中4边界区域梯度方向发生畸变，虽再次使用等积环分割，但不能保证分割后的图像中不出现背景区域，为过滤可能出现的背景区域，需要使用阈值600过滤。在剩余区域，使用数理统计的方法最终确定本次实验中有效特征点的梯度幅值阈值为400。因此特征点的梯度幅值区间为[400，600]。

图8 梯度幅值计算Fig.8 Gradient Amplitude Calculation

（3）利用梯度方向筛选每个圆环中的有效特征点。图8（a）的梯度方向分布图，如图9所示。同样为过滤可能出现的背景区域，将梯度方向的阈值设为[−80，+80]。根据所得数据进行分析，将有效梯度方向的筛选阈值区间设为[−70，+70]。

图9 原图像的梯度方向3维分布图Fig.9 Gradient Direction 3 Dimensional Distribution of the Original Image

2.3.4 特征匹配

首先将模板图像中的n2个圆环的平均梯度幅值与待检测图像依次进行欧氏距离的比较，得到梯度幅值的特征匹配度。为比

2.3.5 匹配系数MRR的适应性分析

算法MRR 的参数梯度幅值PGA、梯度方向PGD的分析结果，如图10、图11所示。

图10 待检测图像与正确模板的参数三维分布图Fig.10 Three Dimensional Distribution of Parameters Between the Image to be Detected and the Correct Template

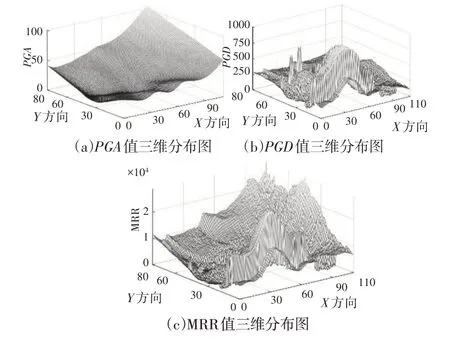
图11 待检测图像与错误模板的参数三维分布图Fig.11 Three Dimensional Distribution of the Parameters of the Image to be Detected and the Error Template

对于PGA匹配，当滑动窗口越接近目标图像所在位置时其PGA指数越低，说明PGA匹配对于目标的位置信息具有越好的描述作用；对于PGD匹配，在滑动窗口的滑动过程中，PGD指数跳变严重，尤其在目标图像所在区域PGD指数变化最为明显，因此PGD对于滑动窗口区域的特征描述能力较强，但由于周边环境对其影响较大，导致其定位能力较弱。根据基于等积环形分割特征的图像识别算法得出的MRR指数，综合了梯度幅值与梯度方向各自的优点，在保留了PGA对于图像定位能力的同时，也加入了PGD对高频元件细节特征的表达能力，因此可以作为一个对于图像定位以及识别的重要参数。

3 实验结果与分析

3.1 实验配置及数据集

实验选用的计算机配置为英特尔酷睿I5−6400（2.7GHz）CPU，NVIDIA GeForce GTX 730 GPU，8.00GB 内存，Windows10系统，实验使用的编译工具为Matlab 2018。

本次验证实验中选择元件共计30种，每种元件选取5张图像。为验证旋转不变性，我们将各个图像绕与轴的旋转角度固定，绕 轴从（0～324）°步长为36°进行旋转，组成1350张图像的测试集。对比试验选用其他4种常用的模板匹配算法，通过实验将本算法与ARRCH[11]、互信息熵、SIFT、SURF在定位性能、识别性能与时效性上进行比较。

3.2 定位性能对比

为评估各个算法的定位性能，给出一种评估方法用于衡量定位准确度的指标ACC：

式中dM1—目标图像的中心位置；dM—待检测模板中准确区域的中心位置；D—目标图像的对角线长，ACC对比结果，如图13所示。从图13中可以看出，提出的算法在定位性能上与同类算法相比有所提升，其ACC值均保持在0.945以上。

图12 5种算法的ACC对比结果Fig.12 ACC Comparison Results of Five Algorithms

3.3 识别性能对比

使用1350张测试图像比较SURF、ARRCH、互信息熵、SIFT及本算法的识别性能，将识别的准确率作为识别性能的对比指标结果，如表1所示。根据表1所示的对比结果，本算法对高频元件的识别准确率达到了95.9%，在识别性能上高于其他4种算法。

表1 识别性能对比结果Tab.1 Comparison Results of Recognition Performance

3.4 时效性对比

使用1350张测试图像来比较5种算法的时效性，以每张图的平均处理时长作为对比指标结果，如表2所示。

表2 时效性对比结果Tab.2 Time Effect Comparison Results

由于本算法使用了较复杂的计算过程，不可避免的在分析图像的时间上有所增加。根据表2所示的对比结果，处理每张图像的平均时长为10.4s。

4 总结

针对高频元件纹理复杂、相似度高，因而不能用传统模板匹配技术进行区分及定位的问题，提出了一种基于等积环形分割特征的图像识别算法。使用等积环形分割、改进的Sobel算子卷积，根据其梯度方向及幅值进行计算，综合考虑了匹配过程中定位的精准度以及显著特征点的提取匹配。实验结果表明本算法能够以95.9%的准确率区分外表相似度极高的高频元件，具有实际的应用价值。