多学科可靠性设计优化的协同求解方法
2022-12-30孟欣佳张立香王晓敏
孟欣佳,张立香,王晓敏
(河北工程大学机械与装备工程学院,河北 邯郸 056000)
1 引言
多学科可靠性设计优化(Reliability−Based Multidisciplinary Design Optimization,RBMDO)是将多学科设计优化(Multidisci⁃plinary Design Optimization,MDO)[1]与可靠性分析[2]有机结合,使复杂产品的设计可以充分利用各学科间相互作用的协同效应达到整体最优,同时保证产品具有足够的可靠性,从而达到提高产品性能和缩短设计周期的目的。该技术被认为是解决不确定性因素影响下复杂产品设计优化问题的有效方法[3],已经在航空航天、汽车、机器人等领域得到了应用[4−6]。
RBMDO 过程中不仅要执行确定性MDO(Deterministic MDO,DMDO),还要对每一次得到的优化值进行多学科可靠性分析(Multidisciplinary Reliability Analysis,MRA),而且DMDO 和MRA都需要进行多学科分析,也就是说RBMDO是一个确定性优化、可靠性分析、多学科分析三重嵌套的循环寻优过程[7],这使得采用RBMDO进行复杂产品设计时产生了高昂的计算花费,严重阻碍了RBMDO的进一步工程应用。
目前,针对RBMDO问题的解耦主要是以单学科下的序列可靠性设计优化(Sequential Optimization and Reliability Assess⁃ment,SORA)方法[8]为基础,将嵌套循环的RBMDO解耦成确定性优化和可靠性分析顺序执行的过程,同时将多学科分析集成到顺序执行的确定性优化和可靠性分析环节中。
文献[9]将单学科可行性分析法(Individual Disciplinary Feasi⁃ble,IDF)和多学科可行性分析法(Multidisciplinary Feasible Ap⁃proach,MDA)应用到SORA 框架中,分别提出了RBMDO 问题的IDF−SORA和MDA−SORA求解方法。文献[10]以SORA法为基础,结合层次思想和凸线性化近似技术,提出一种混合层次的序列化RBMDO计算框架。
文献[11]将基于近似并行子空间优化策略(Approximate Con⁃current Subspace Optimization,ACSSO)和角度更新功能测度法应用到RBMDO 过程,提出了ACSSO−SORA 求解方法。文献[12]对SORA法进行改进,提出了基于增量移动矢量法的RBMDO求解方法。
在前述研究的基础上,提出一种多学科协同可靠性设计优化方法(Multidisciplinary Collaborative Reliability Design Optimi⁃zation,MCRDO)。该方法利用可靠性分析的性能测量法(Perfor⁃mance Measure Approach,PMA)和库恩−塔克(Karush−Kuhn−Tucher,KKT)条件将多学科可靠性约束等效为确定性约束,然后基于CO策略的思想,将RBMDO 问题分解成并行的单学科优化问题,采用一致性约束对各学科进行协调,从而达到多学科可靠性设计优化的并行执行。
2 多学科协同可靠性设计优化方法
2.1 多学科可靠性设计优化的数学模型
当耦合的多学科系统中含有随机不确定性时,考虑不确定性产生的影响,RBMDO方法以各学科性能概率约束的方式来保证复杂产品的可靠性,其典型的优化数学模型为:

式中:d—确定性设计变量;x—随机变量;p—随机型的设计参量,即随机参数;μx—随机变量x对应的均值;μP—随机参数p对应的均值;f—目标函数;Gi—第i个学科所有的随机型性能约束函数;gi—第i个学科所有确定性性能约束函数;L—边界约束的下限;U—边界约束的上限;下角标i—第i个学科;y•i—耦合变量,其值是通过下式(2)的学科分析获得的:

式中:y•i—耦合变量的一般表示形式,其中下角标中的•表示该耦合变量的产生来源,下角标中的i表示该耦合变量要输往的学科分析。
优化模型(1)中的多学科概率约束可以利用性能测量法进行评估,此时典型的RBMDO模型可被转化为:

式中:下角标iMPP—该变量∕参量取逆最有可能失效点处的值。
在式(3)的优化过程中,每次迭代寻优时xi−iMPP、piMPP和y•i−iMPP均为定值,但每次迭代求解出设计变量后,都需要经过一次多学科可靠性约束的评估,以确定下次迭代时xi−iMPP、piMPP和y•i−iMPP的值。
2.2 多学科可靠性约束的等效
对RBMDO模型(3)中的多学科可靠性约束的评估通常由式(10)所示的优化问题获得,即式(3)中每次迭代的xi−iMPP、piMPP和y•i−iMPP值可通过式(4)求解获得。

式中:u=[uxi,uP]—随机变量xi和随机参数p向标准正态U空间转化后的变量;hequ—学科耦合方程的等式约束形式。
上述式(4)属于含等式约束的优化问题,其最优点满足KKT条件,即:

式中:∇u,y— 对u和y求偏导。

2.3 多学科可靠性设计优化的协同求解
在性能测量法和KKT 条件等效的基础上,典型的RBMDO模型可以转化为一个确定性优化求解模型,为:

式中:下标i−iMPP—对应于第i个学科iMPP点的量;下标m—对应于随机均值的量;ui−iMPP—第i个学科U空间的iMPP,由随机变量和随机参数的iMPP组成,即ui−iMPP=[uxi−iMPP,upi−iMPP];xi−iMPP—随机变量在X空间的iMPP;pi−iMPP—随机参数在X空间的iMPP;yi−iMPP—对应于随机变量和随机参数的iMPP的耦合变量;yi−m—对应于随机变量和随机参数的均值的耦合变量;λi—第i个学科可靠性分析的拉格朗日乘子矢量。
值得注意的是,在该优化模型中,xi−iMPP、pi−iMPP、uxi−iMPP和λi均为变量称为辅助设计变量,而yi−iMPP称为辅助耦合变量,统称为辅助变量;这些辅助变量不需要再额外的通过式(4)的优化模型去求解,而是随着设计变量[d,μx]通过式(6)直接求解获得。
借助CO策略[13]上述优化模型(6)可以分解一个并行协同执行的设计优化过程,即分解为系统级优化和子系统级优化两个层次。在子系统级,各学科独立并行执行本学科的可靠性设计优化,而系统级则执行对每次优化结果的协调,其具体的优化模型为:
系统级:

式中:d̂i—系统级传递给第i个学科的确定性变量的副本;μ̂i—系统级传递给第i个学科的随机变量均值的副本;ûi−iMPP—系统级传递给第i个学科的iMPP点的副本;ŷi−m—系统级传递给第i个学科的对应于随机均值的耦合变量的副本;ŷi−iMPP—系统级传递给第i个学科的对应于iMPP点的耦合变量的副本。
上述式(7)和式(8)所示的系统级和子系统级优化模型共同构成了所提MCRDO方法的数学模型,具体计算流程,如图1所示。MCRDO主要的计算步骤包括:

图1 MCRDO计算流程图Fig.1 Flow Chart of MCRDO
(1)初始化。设定初始的迭代步数k=1,定义确定性设计变量d、随机变量x、随机参量p的均值和均值的初始值,设定迭代的收敛精度ε,并通过设计变量的初始值计算耦合变量的初始值y;
(2)系统级目标值分配。将当前的设计变量值依据所属学科分配到各子系统,分配的值包括d̂i、μ̂i、ûi−iMPP、ŷi−m和ŷi−iMPP;
(3)并行的子系统级优化。在分配的系统级目标值的基础上,各学科并行的执行单学科的可靠性设计优化,优化模型为式(7);
(4):系统级优化。在各子系统优化结果的基础上,构建一致性约束条件,并执行系统级优化,其优化模型为式(7);

(6)获得满足可靠约束下的最优设计方案。
3 算例验证及分析
3.1 数值算例
该算例[9,14]包括3个确定性变量、3个随机参数和2个耦合变量,多学科优化框架,如图2所示。

图2 数值算例优化框架Fig.2 Optimization Framework of Numerical Example
该算例中,随 机 参 数均服从正态分布:xs∼N(0,0.3),x1∼N(5,0.5),x2∼N(1,0.1);可 靠 度 取 值 为R1=R2=Φ(β)=Φ(3)=0.9987,Φ为标准正态分布。
采用不同RBMDO求解方法对式(9)进行求解,其结果,如表1所示。绘制这里所提方法求解的迭代历程,如图3所示。
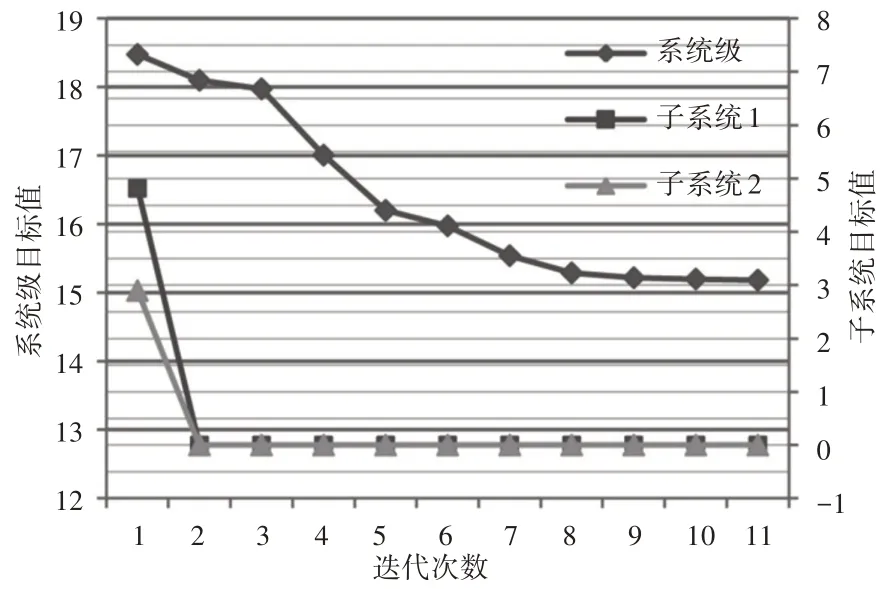
图3 数值算例迭代历程图Fig.3 Iteration Process of Numerical Example
表中:Nf—函数评估次数;Nv—变量个数。
IDF−SORA和MDF−SORA方法的结果来源于文献[9]。由表1可知,在优化点处两个学科的性能函数g1和g2的值均在各自的可靠区域内,且学科1的性能函数值接近于0,即位于可靠与失效的临界状态。同时结合图3可知,子系统1和子系统2的优化过程是并列执行的,除初始值外子系统级的一致性协调函数值均接近于0,系统级在经过8次迭代后,系统级目标函数值的变化逐渐趋于稳定,最终于第11次迭代时达到收敛。由此说明在满足可靠性约束条件,同时满足协同求解一致性约束条件的情况下,求解结果已经达到了最优状态。

表1 数值算例优化结果Tab.1 Optimal Results of Numerical Example
由表1亦可知,采用所提的MCRDO方法求解的设计变量值和目标函数值与采用序列方法的IDF−SORA、MDF−SORA 求解的结果一致,但是所用的函数评估次数是三种方法中最少的。这说明MCRDO方法可在保证求解精度的同时,使得计算的花费最小。此外,采用MCRDO 方法求解时,优化涉及到的总变量数为21个。采用IDF−SORA方法时,确定性优化与可靠性分析的总变量数为15个。而采用MDF−SORA方法时,其外显的变量个数为9个,用于内部学科分析的变量是6个,总变量数亦是15个。这是由于MCRDO方法在优化求解时,利用KKT条件将确定性分析与可靠性分析进行统一优化时,增加了各学科可靠性分析所对应的拉格朗日乘子变量,增加了额外的辅助变量。
3.2 工程设计实例
该工程实例为一复合缸的多学科可靠性设计优化。该复合缸由内缸和外缸两部分组成[15−16],其结构,如图4所示。
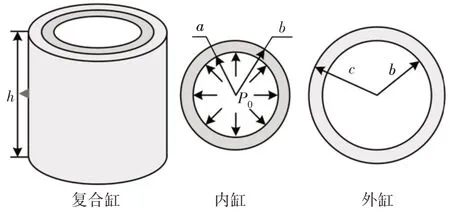
图4 复合缸结构图Fig.4 Sketch of the Compound Cylinder
该多学科可靠性设计优化问题由内缸和外缸两个子系统组成,每个子系统包含4个可靠性约束条件,具体优化模型为:

该多学科可靠性设计优化问题共包括6个随机不确定性量,其中3个为随机变量,3个为随机参量,其分布参数,如表2所示。

表2 复合缸随机不确定性量分布Tab.2 Random Uncertainty Distribution of Compound Cylinder
该问题中,内外缸的最大等效应力和不同半径处的最大切应力均是关于随机不确定性量的隐函数,在此通过ANSYS 和MATLAB的联合仿真,再利用数据拟合获得[16]。利用本文所提的方法对该问题进行求解,其结果,如表3所示。同时绘制该复合缸多学科可靠性设计优化的迭代历程,如图5所示。
由表3可知,子系统1和子系统2的约束函数在MPP点处的函数值均小于等于0,说明优化结果满足可靠性要求。且约束函数g1的值近似等于0,说明该优化结果已达到了最优。表3中,第一行数据是在不考虑不确定性的情况下获得的确定性设计优化结果,其余4行是在考虑不确定性的影响下,采用不同求解方法获得的可靠性设计优化结果。由表3可知,可靠性设计优化求得的最大目标值比确定性优化求得的值要小,说明在考虑不确定性影响的情况下,可靠性设计优化的结果比确定性优化结果更保守,设计结果也更可靠。由此设计的复合缸,在受到外来因素干扰时,可在一定范围内仍然满足其性能要求。
由表3还可看出,不同RBMDO求解方法获得的最优值和随机变量的优化值均比较接近,且传统的三层嵌套方法需要的函数评估次数最多,而这里所提的MCRDO方法需要的函数评估次数最少。图5表明,在对该复合缸进行多学科可靠性设计优化时,采用IDF−SORA、MDF−SORA、MCRDO三种方法求解时,所需的收敛次数分别为20、19和16。由此说明本文所提的MCRDO方法相对于IDF−SORA、MDF−SORA 具有较好的计算效率。这主要有两个原因:(1)由于MCRDO在求解时,利用KKT条件将可靠性分析环节嵌入到确定性优化中,使二者一起完成分析,减少了可靠性分析环节;(2)由于求解时采用了协同优化设计的原理,将不同学科并行执行,避免了MDA分析和优化的分割操作,提高了计算效率。
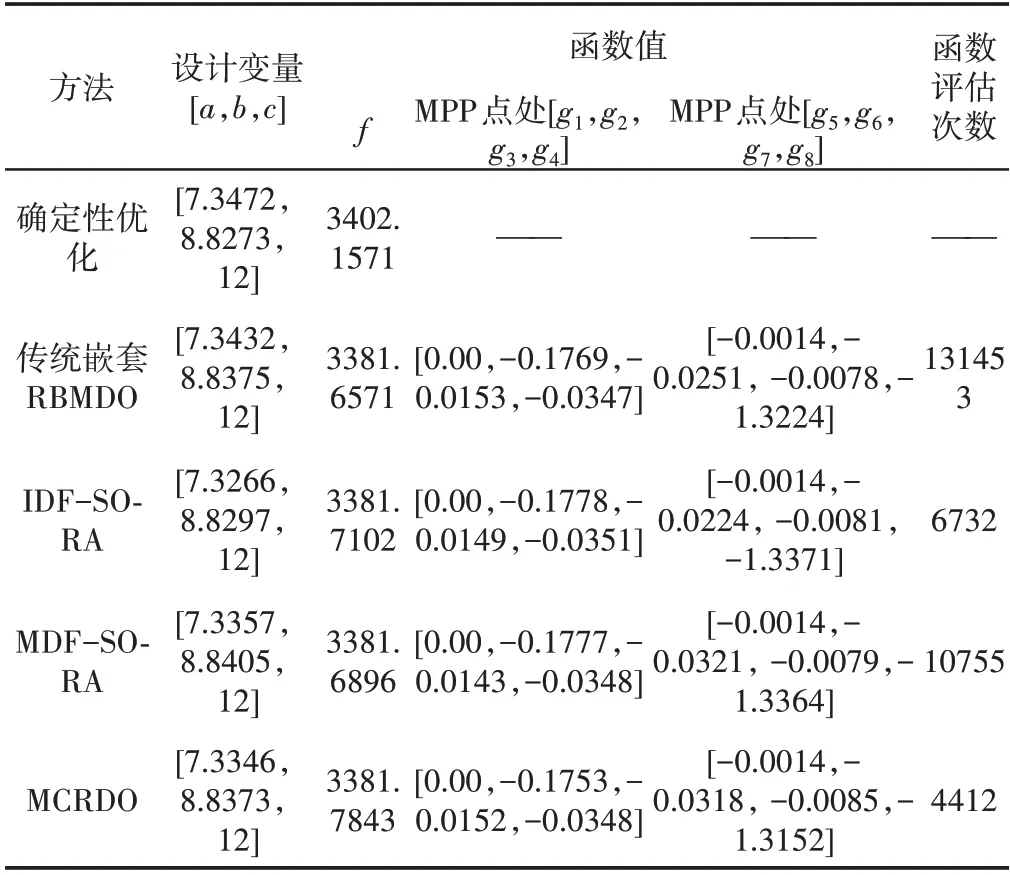
表3 复合缸多学科可靠性计优化结果Tab.3 Results of Multidisciplinary Reliability Optimization of Compound Cylinder

图5 复合缸多学科可靠性设计优化迭代历程Fig.5 Iteration Process of Multidisciplinary Reliability Optimization of the Compound Cylinder
4 结论
(1)基于性能测量法和KKT条件提出了一种多学科协同可靠性设计优化方法。该方法将多学科的可靠性设计优化问题分解成几个并行的子学科优化问题和一个用于协调子学科优化结果的系统级优化问题,实现了复杂产品设计时各学科可靠性设计优化的并行执行,扩展了多学科可靠性设计优化的学科自主性。
(2)由于所提MCRDO是并行执行的寻优过程,其求解计算效率要高于嵌套循环式的RBMDO 和基于SORA 的RBMDO 方法。数值算例和工程实例均表明MCRDO 能够实现多学科可靠性设计优化的并行执行,且其计算效率要优于传统嵌套RBMDO、IDF−SORA和MDF−SORA。
(3)由于采用了KKT条件对多学科可靠性约束进行等效,等效后的优化模型较初始的RBMDO模型增加了额外的辅助变量,且初始设计优化问题越复杂,变量越多,等效后的优化模型的额外变量也会越多,这会进一步增加求解的计算花费,为此如何减少由于等效带来的额外变量的数量是下一步需要解决的问题。
