自由漂浮双臂空间机器人末端轨迹跟踪控制

王 琪，孔德彭

（1.浙江省机电技师学院电气工程系，浙江 义乌 322000；2.浙江工业大学机器人教育研究中心，浙江 杭州 310000）

1 引言

空间机器人可以代替人类更安全、更精确、更便捷地完成空天科研实验和生产作业，得到广泛的研究并已大量应用于太空在轨服务任务[1−4]。由于太空环境中机器人的基座与机械臂之间运动相互干扰，导致其运动控制问题十分复杂且种类各异[5−8]。其中，根据机器人基座受控情况，可区分为自由漂浮、姿态受控、位置受控和基座固定四种状态下的运动控制；根据机械臂的数量区分，可分为单臂和多臂空间机器人运动控制；根据研究的空间不同，又可分为关节空间和惯性空间运动控制。

综合考虑燃料损耗、系统稳定性、执行任务可靠性等实际工程因素，自由漂浮状态下多臂空间机器人惯性空间末端的运动控制问题更具研究价值。文献[9−10]结合增广变量思想，分别提出一种鲁棒控制和自适应控制方法，实现了自由漂浮双臂空间机器人（Dual−Arm Free Floating Space Robot，DFFSR）末端抓手跟踪期望轨迹运动控制，但均需要实时测量基座角速度和角加速度信息；文献[11]针对惯性参数未知DFFSR惯性空间运动控制问题，设计了一种基于速度滤波器的鲁棒控制方法，实现了末端轨迹精确跟踪，但该控制方法未考虑外界扰动；文献[12]针对具有外部扰动和不确定载荷情况下的DFFSR末端运动控制问题，设计了一种拟增广鲁棒与自适应混合控制方法，实现了末端轨迹精确跟踪且大大减少了计算量。上述文献较好的解决了DFFSR动力学方程惯性参数呈非线性关系的问题，但均未考虑能量优化问题。

针对DFFSR系统机械臂末端轨迹跟踪控制问题，提出了一种增广优化控制方法。首先，基于DFFSR关节空间的动力学方程和运动学方程，推导出其机械臂惯性运动空间动力学方程；而后，基于增广变量思想，将动力学方程扩展成以末端位置和线速度为状态变量的伪线性状态方程，获取系统SDC（State−depen⁃dent Coefficient）矩阵，以此提出一种增广SDRE优化控制方法，并给出能量优化指标，通过Lyapunov方法证明系统渐近稳定性；一个针对平面二连杆的DFFSR系统数值仿真验证了所提控制方法的可行性。

2 系统建模

2.1关节空间动力学方程

DFFSR系统由基座M0及机械臂M1、M2、M3、M4组成，如图1所示。

式中：M(q) ∈R5×5—正定−对称质量矩阵；C(q，q̇)q̇h∈R5—包含哥氏力和离心力的广义列向量，且满足如下性质：

（1）M(q) ∈R5×5对称正定且有界。

（2）对于任意向量Z∈R5，存在zTṀ(q)z= 2zTC(q，q̇)z。

2.2 系统运动学方程

式中：K∈R1×4—基座姿态角速度与关节角速度的雅克比关系向量；Jmh(q) ∈R2×5—基座线速度与姿态角及关节角速度的雅克比关系矩阵；J(q) ∈R4×7—双臂末端抓手线速度与基座线速度、姿态以及关节角速度之间的广义雅克比关系矩阵，其表达式为：

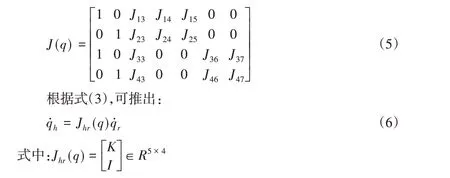
2.3 系统惯性空间动力学方程

3 控制器设计

3.1 预备知识

考虑仿射非线性系统：

3.2 基于增广变量优化控制器设计

3.3 稳定性分析

4 数值仿真

以图1所示平面二连杆DFFSR系统为对象，进行数值仿真。选定其惯性参数为：

仿真时长t= 20.0s，如图2～图4所示。其中，DFFSR左臂末端位置及其在x、y轴坐标分量的轨迹跟踪效果，如图2 所示。DFFSR右臂末端位置及其在x、y轴坐标分量的轨迹跟踪效果，如图3所示。DFFSR机械臂各关节控制力矩变化曲线，如图4所示。

在图2 和图3 的仿真结果中，左∕右机械臂末端在惯性坐标系下x方向以及y方向分量的轨迹跟踪情况，图中横坐标为仿真运行时间，纵坐标为机械臂位置的分量坐标值，如图2（a）、图3（a）所示。从图中可以看出，两个分量坐标能够克服初始误差迅速实现对期望轨迹的跟踪；左∕右机械臂末端在惯性坐标系下运动轨迹的跟踪情况，如图2（b）、图3（b）所示。图中横坐标为机械臂位置的x坐标分量，纵坐标为机械臂位置的y坐标分量，期望运动轨迹为一个圆形轨迹，从图中可以看出，机械臂末端能够从初始点位迅速运动到期望点位并对期望轨迹进行跟踪；左∕右机械臂末端在惯性坐标系下x方向以及y方向的轨迹跟踪误差，如图2（c）图3（c）所示。图中横坐标为仿真运行时间，纵坐标为期望轨迹与实际轨迹的跟踪误差值，从图中可以看出，x方向和y方向的轨迹跟踪误差均保持在一较小范围内，进一步证明了控制器的有效性。

在图4的仿真结果中，左∕右机械臂各关节铰的输出力矩，如图4（a）、图4（b）所示。图中横坐标为仿真运行时间，纵坐标为关节铰输出力矩值，从图中可以看出，左∕右机械臂的两个关节铰出初始输出力矩较大外，后续持续输出力矩均很小，在一定程度上实现了输出力矩的优化，满足实际工程需求。

综合分析仿真结果，图2、图3验证了所设计控制器能实现机械臂末端对期望轨迹的快速跟踪，且误差保持在合理范围内；图4表明所提优化控制方法在保持跟踪精度的同时对输出力矩进行了能量优化，除存在初始冲击力矩外，后期控制输出力矩值均很小。

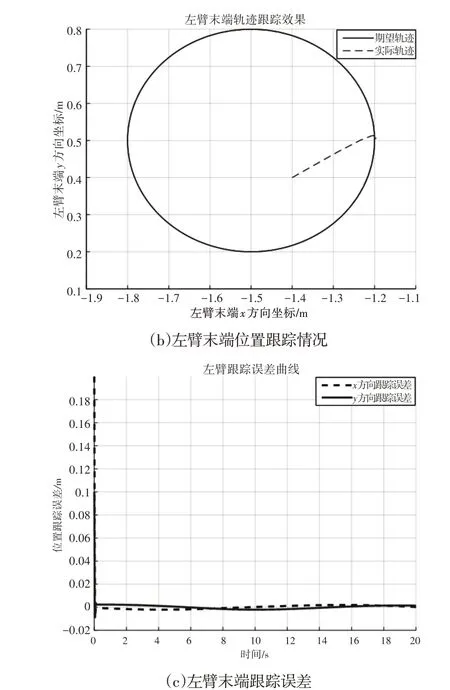
图2 左臂末端位置跟踪效果Fig.2 The End Position Tracking Effect of Left Arm

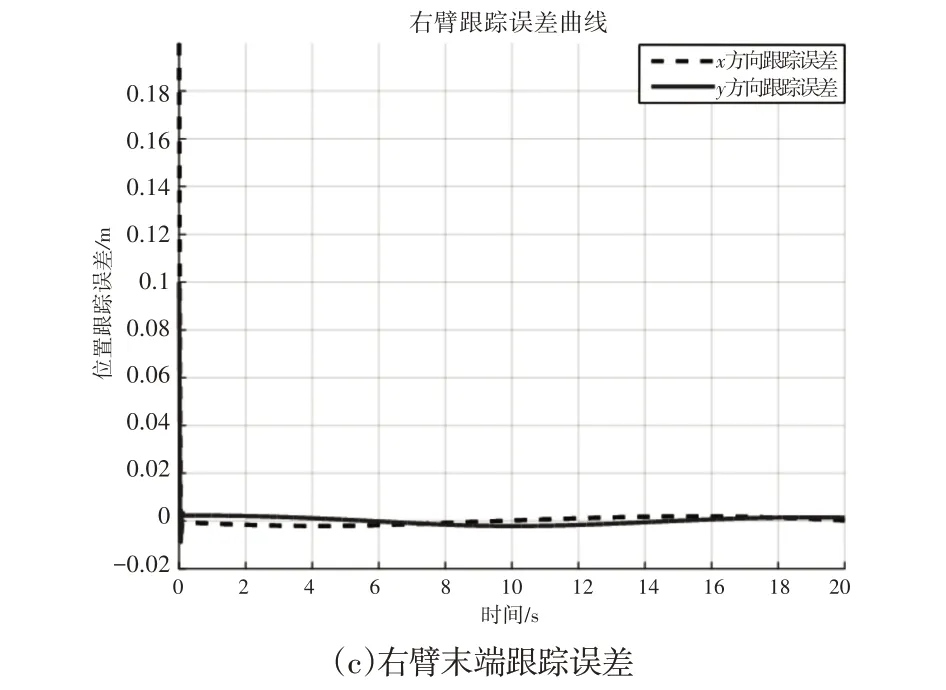
图3 右臂末端跟踪效果Fig.3 The End Position Tracking Effect of Right Arm

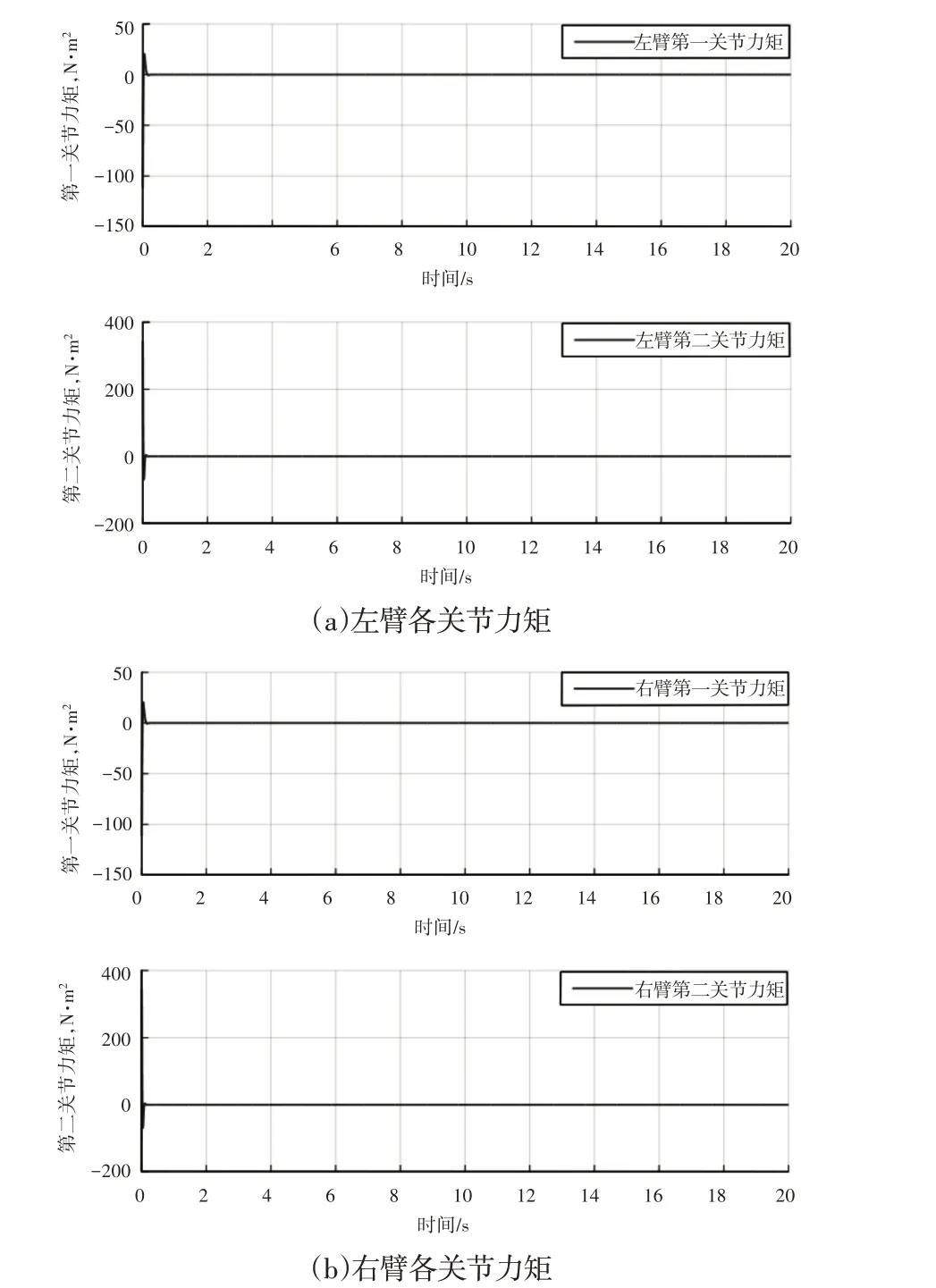
图4 各关节控制力矩Fig.4 The Control Torque of Each Joint

5 结论

根据DFFSR关节空间的动力学方程和运动学方程，推导出其机械臂惯性运动空间动力学方程，并基于增广变量思想，将动力学方程扩展成以末端位置和线速度为状态变量的伪线性状态方程，以此提出一种增广状态依赖Riccati方程（SDRE）优化控制方法，实现了DFFSR系统末端位置的快速有效跟踪。所提控制方法通过增广变量实现了末端位置和速度的同步跟踪，大大提高了跟踪速率，且考虑了能量优化问题，使得输出控制力矩较小。