基于质心自适应选取的密度万有引力聚类算法

陈金鹏，李睿熙，杨 然，安俊秀+

(1.成都信息工程大学 并行计算实验室，四川 成都 610225；2.成都锦城学院 计算机与软件学院，四川 成都 611731)

0 引 言

聚类分析是大数据分析中极其重要的方法之一，目的是将多个对象按照其相似性划分成多个差异度较大的类，而这些类别中的对象相似度较高。划分聚类算法[1]是在给定数据集的基础上，通过一些相似性度量的公式，将这些数据点划分成多个簇，每个簇中的点相似度较高而不同的簇之间相似度较低[2]。基于划分的聚类算法有很多种，其中最典型的聚类算法是K-means算法[3]，该算法的主要思想是通过迭代计算不同数据点和给定簇中心的距离不同而分配给距离最近的簇。然而传统的K-means算法有4大缺陷，这些缺陷主要是聚类效果对初始簇中心的选取结果具有依赖性[4,5]，k值难以确定[6,7]，没有考虑簇与簇之间的关系[8]，只能发现圆簇以及离群点对聚类效果有影响[9]。基于以上问题，Chunhui Yuan等在文献[10]中针对k值选择的不同，导致的聚类结果差距较大的问题，给出了4种k值选择方法，即肘部法、间隙统计、轮廓系数和Canopy算法。王建仁等在文献[11]中对肘部法进行了详细的实验和运用，通过k值和“肘点”的关系来确定k值点，提出了ET-SSE算法，该算法可以改进k值的选择。

万有引力聚类是将物理学中任意两个粒子之间都存在相互吸引的引力这一思想引入到聚类中，使得聚类过程中不仅要考虑数据之间的距离，还要考虑数据的“质量”，杜洁等在文献[12]中提出数据的“质量”可以使用局部合力来代替，使得数据点之间的关系变得更加紧凑，使用局部合力来替代万有引力公式中的质量也为万有引力在聚类算法中的应用起到了至关重要的效果。引力搜索算法GSA[13]将物理学的万有引力作为算法核心进行了研究，为后续的引力算法研究奠定了基础，该算法也存在一些缺点，容易早熟收敛，并且存在需要设定较多参数值的缺点。基于GSA算法的提出，Chao Liu等在文献[14]中对粒子初始位置进行了优化，提出了AC-GSA算方法，该算法将自适应惯性权重系数引入到公式中。Seyedali Mirjalili等在文献[15]中对引力系数G进行了改进，使得算法能够突破局部最优解对全局聚类的影响。魏康园等在文献[16]中针对经典的引力搜索算法很容易在搜索的过程中得到一个局部最优解，从而很早发生收敛的现象提出了A2F-GSA算法，该算法相比其它算法拥有更好的收敛性。Chen Lei等在文献[17]中提出了Gravc算法，该算法通过设计一种基于局部密度的数据压缩策略，减少了参与引力聚类算法的数据对象数量和每个对象的邻域数量，并对传统的重力模型进行了优化，以适应数据压缩策略造成的不同对象的质量差异。引力聚类的思想可以用于其它多种聚类算法的改进中，王治和等在文献[18]中将引力聚类思想运用在AP算法中，通过对偏向参数的依赖性的降低，极大地提高了稀疏数据集的聚类最终效果。肖辉辉等在文献[19]中将引力聚类思想运用在FPA算法中，较大提升了FPA算法的收敛速度、收敛精度、鲁棒性。Zhiqiang Wang等在文献[20]中根据引力模型推导出中心点度量，并区分了内部点和边界点，提出了局部引力LGC聚类算法，由于该算法需要确定多个参数且对参数取值敏感，因此该作者将社团聚类引入其中，提出了CLA算法，该算法将LGC算法的参数减少到了1个，但是聚类效果相对下降。

1 基于密度万有引力的K-means改进算法

任意两个空间中的粒子之间都存在相互吸引的万有引力，牛顿的万有引力定律认为这个力的大小与它们本身的质量以及它们之间的距离有关。万有引力的大小与质量成正比例关系，与距离成反比例关系，这个力的计算公式如式(1)所示

(1)

式中：mi和mj分别代表粒子i与粒子j的质量，G表示引力常量，其值约为6.67×10-11N·m2/kg2，dij为粒子i与粒子j之间的距离。

针对传统的K-means方法通过距离和中心点进行聚类时没有考虑簇与簇之间关系的问题，本文根据万有引力公式进行了改进，并引入了K-means聚类中。从文献[12]中提出公式中的“质量”可以通过其周围的点到此簇中心的局部合力来近似替代，本文通过引入“密度”的概念来近似替代此处的局部合力，因此，本文在万有引力公式中做了如下改动：由于G是常量，在引力大小比对中可以忽略不计；万有引力中粒子的质量，在本文中采用密度来进行改进计算，如式(2)所示

(2)

定义1 簇的密度ρi： 万有引力的大小与粒子的质量成正比，而在数据集中粒子的质量不可度量，而粒子在空间中的局部密度是可以度量的，因此本文万有引力公式中的质量，结合文献[12]所提出的办法进行改进，簇的密度ρi可用近似替代万有引力公式中的质量，其大小与簇中粒子和簇中粒子之间的距离有关，簇的密度ρi计算公式如式(3)所示

(3)

式中：K为簇内点的数目，Ri为簇内点到簇中心的距离。

定义2 圆簇：以簇中心为圆心，这个簇中距离簇中心最远的点到簇中心的距离为半径作圆，若此簇中所有点都在这个圆内，则称这个簇为圆簇；反之，为非圆簇。

定义3 空簇：若一个簇中不包含任何数据点，则称此簇为空簇。

由于空间中的单个点被视为质量大小都相同的点，因此，每个点的密度也都相同，即ρj都相同；在计算过程中，常量G与ρj一样，都不会影响不同点之间的密度万有引力的相对大小，因此，ρj的处理办法与G一样可以忽略不计。结合式(2)和式(3)，最终粒子之间的密度万有引力θ定义如式(4)所示

(4)

式(4)定义了数据集中点与点之间、点与簇的密度万有引力公式，使用密度万有引力作为K-means聚类中的欧氏距离，如算法1所示，本算法的优势在于将引力因素加入到了聚类算法中，可以发现非圆簇；另外如果在过程中出现了空簇，则直接删除。

算法1：基于密度万有引力的K-means改进算法

算法的输入：含有S个点数据集S，聚类个数K。

算法的输出：得到的结果是k个簇。

步骤1 选取K个点作为初始聚类簇中心。

步骤2 重复步骤3、步骤4、步骤5。

步骤3 根据式(4)分别计算每个样本点到K个簇中心的密度万有引力，将其分配给引力最大的簇。

步骤4 更新簇的中心和簇的质量，重新计算簇平均值。

步骤5 删除不包含任何点的簇，并令k=k-1。

步骤6 直到所有簇中心不再变化，循环结束。

普通K-means算法在聚类时使用的是欧氏距离来对簇进行划分，这种办法只考虑了两点之间的距离，算法1使用改进的万有引力密度公式替代了普通K-means算法的欧式距离公式，使得在聚类过程中不仅考虑了两点之间的距离，还考虑了当前簇的大小对点的影响。当前簇密度越大，与点距离越近，则该簇对点存在的吸引作用就越大，最终将此点聚类。

2 基于质心自适应选取的密度万有引力聚类方法

2.1 基于质心自适应选择的聚类簇中心选取算法

对于K-means算法中，每次需要给定簇的数量k，由于k值选择的不同，聚类的最终结果会不同；另外在初始给定的k值相同的情况下，由于初始簇中心随机选择不同，也会造成最终聚类的结果不同，因此本文提出了一种基于质心自适应选择的聚类簇中心选取算法，该算法通过设置一种初始簇中心的选取策略，来控制选择更好的初始簇中心和自适应选择k值，从而达到减少迭代次数和更好的聚类效果。

该算法设有以下定义：

定义4 状态标记：簇中每一个点都拥有自己的一个状态标记，若该点的标记为0，则该点需要进行遍历改变状态；若该点的状态t=-1， 则该点可能是离群点；若该点的状态为t(t=0,1,2,…)， 则该点被t个簇中心所包含。

定义5 初始圆：以数据集中心点X和一个标记t=0的点N组成的线段XN的长度为直径，线段XN的中点为圆心作出的圆称为初始圆。

定义6 簇圆：以初始圆包含的点的质心M为圆心，线段MX的长度为半径作出的圆称为簇圆。

欧式距离[19]是聚类分析中最常用的公式，其本质是对两个对象之间最直观的直线距离进行计算，欧式距离的计算公式如式(5)所示

(5)

式中：dij为欧氏距离，xij代表数据对象1，yij代表数据对象2，n代表数据对象的个数。

本文中基于质心自适应选择的聚类簇中心选取算法以数据集的中心点作为参照物，然后从离中心点最远的点开始不断作初始圆和簇圆，并同时改变本数据集中所有的点的标记值，然后根据数据集本身的密集程度来划分出簇中心和离群点，算法具体过程如算法2所示，本算法的优势在于可以在一定程度上找到离群点，并且可以为后续聚类减少迭代次数，也不需要一开始给定k值。

算法2：基于质心自适应选择的聚类簇中心选取算法

算法的输入：含有S个点数据集S。

算法的输出：得到的结果是k个簇中心和状态标记不同的点。

步骤1 首先计算整个数据集的质心，以此质心作为整个数据集的中心，记作X。

步骤2 计算数据集中每个点到数据集中心X的距离，并将这个距离按照由大到小排序，每个点按此顺序分别记作xi， 距离记作di，i从1到S，并将每个点的初始状态记为t=0。

步骤3 按照步骤2中的排好顺序的点，从x1开始到xS， 依次遍历状态标记为0的点。

步骤4 重复步骤5、步骤6、步骤7。

步骤5 根据此点xi和整个数据集的质心X，做出初始圆，并将此点xi状态标记为t=-1。

步骤6 以此初始圆内的所有点作为一个整体，计算为此圆的质心Y，做出簇圆，并将簇圆中所有点的状态数值t=t+1， 如果这个点是离群点(即状态标记t=-1的点)，则这个状态数值t=t+2。

步骤7 直到所有点的状态都不为0，循环结束。

常规的K-means聚类算法对于初始点的选择是随机的，其改进算法也存在较多的选择，会导致初始选举不一致导致聚类结果不一致。本文算法2可以以数据集质心作为出发点，并向周边扩展寻找簇中心，得到唯一的初始选举结果，且该初始结果在数据集全面覆盖分布均匀。该算法与已有算法相比较，算法实现简单，并且可以较好地确保一开始选择的初始簇中心和分配的点位于各个簇的中心位置，所得到的k值为本次聚类中最大的簇数目，并覆盖数据集中所有的点。

2.2 基于质心自适应选取的密度万有引力聚类算法

基于质心自适应选取的密度万有引力聚类(CASG-means)算法首先根据算法2对簇中心进行选择，然后通过算法1的改进算法思路进行结合，最终得到了算法3的聚类算法，CASG-means算法改进的具体步骤如图1所示。

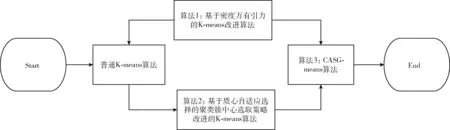
图1 CASG-means算法改进的步骤

算法3：基于质心自适应选取的密度万有引力聚类算法

算法的输入：含有S个点数据集S。

算法的输出：得到的结果是k个簇，以及标记为t=-1的离群点。

步骤1 执行算法2，得到k个簇和状态标记不同的点。

步骤2 对每个标记状态t=1的点，直接分配给步骤1最终所在的簇中，并更新每个簇的簇中心。

步骤3 重复步骤4、步骤5、步骤6、步骤7。

步骤4 对标记t>0的所有点(第一次循环不再分配状态标记t=1的点)，根据式(4)分别计算每个样本点到K个簇中心的密度万有引力，将其分配给引力最大的簇。

步骤5 更新簇的中心和簇的质量，重新计算簇平均值。

步骤6 删除不包含任何点的簇，并令k=k-1。

步骤7 直到所有簇中心不再变化，循环结束。

算法3结合了算法2的基于质心自适应选择的聚类簇中心选取策略，并应用了算法1的密度万有引力公式替换欧氏距离，不仅增强了点与点之间、点与簇之间的吸引关系，还解决了算法2中可能存在由于数据分布不均匀导致的多个初始簇中心分布距离较近的问题，对距离较近的簇进行了吸引合并，最终可以自适应生成合适的簇数目，并且可以识别出离群点。与现有的改进算法相比较，具有实现简单、可以根据数据点的实际分簇情况对簇进行合并的优势。

3 实验与分析

本章将对本文所提出的算法3：基于质心自适应选取的密度万有引力聚类算法(CASG-means算法)进行实验，所涉及到的实验分别为聚类效果对比实验、迭代次数、离群点数目和簇减少数目。

3.1 实验环境

实验环境配置如下：Intel(R) Core(TM) i7-9750H CPU @2.60 Hz，16 GBytes，Windows 10家庭中文版，所用代码依赖于Python3.6(base)。实验在30个不同的数据集上做了对比效果，数据集为python随机数生成的人工合成数据集，其中簇中心用实心圆点标记，离群点用“x”标记，k值的选择为基于质心自适应选择的聚类簇中心选取策略的簇数目。

3.2 数据聚类效果对比

普通K-means算法较为成熟的改进算法有K-means++算法[22]和ISODATA算法[23]，因此本次实验将本文提出的3个新算法与K-means++算法和ISODATA算法进行对比实验。因此本节将对以下5个算法的聚类结果进行对比：①基于密度万有引力的K-means改进算法；②基于质心自适应选择的聚类簇中心选取策略改进的K-means算法；③基于质心自适应选取的密度万有引力聚类(CASG-means)算法；④K-means++算法；⑤ISODATA算法。

本节数据集选自第一节30个不同数据集中的其中5个经典的例子进行对比说明，在本节的所有实验图中(如图2～图6所示)，每一次实验结果分为6个图片，图(a)是质心自适应选择的聚类簇中心，图(b)是上述算法①结果，图(c)是上述算法②结果，图(d)是上述算法③结果，图(e)是上述算法结果，图(f)是上述算法⑤结果。在本次实验中，所有的k值取值为图(a)所划分出来的簇数目，算法⑤中的最大迭代次数取值为算法③在相同数据集所用的迭代次数。

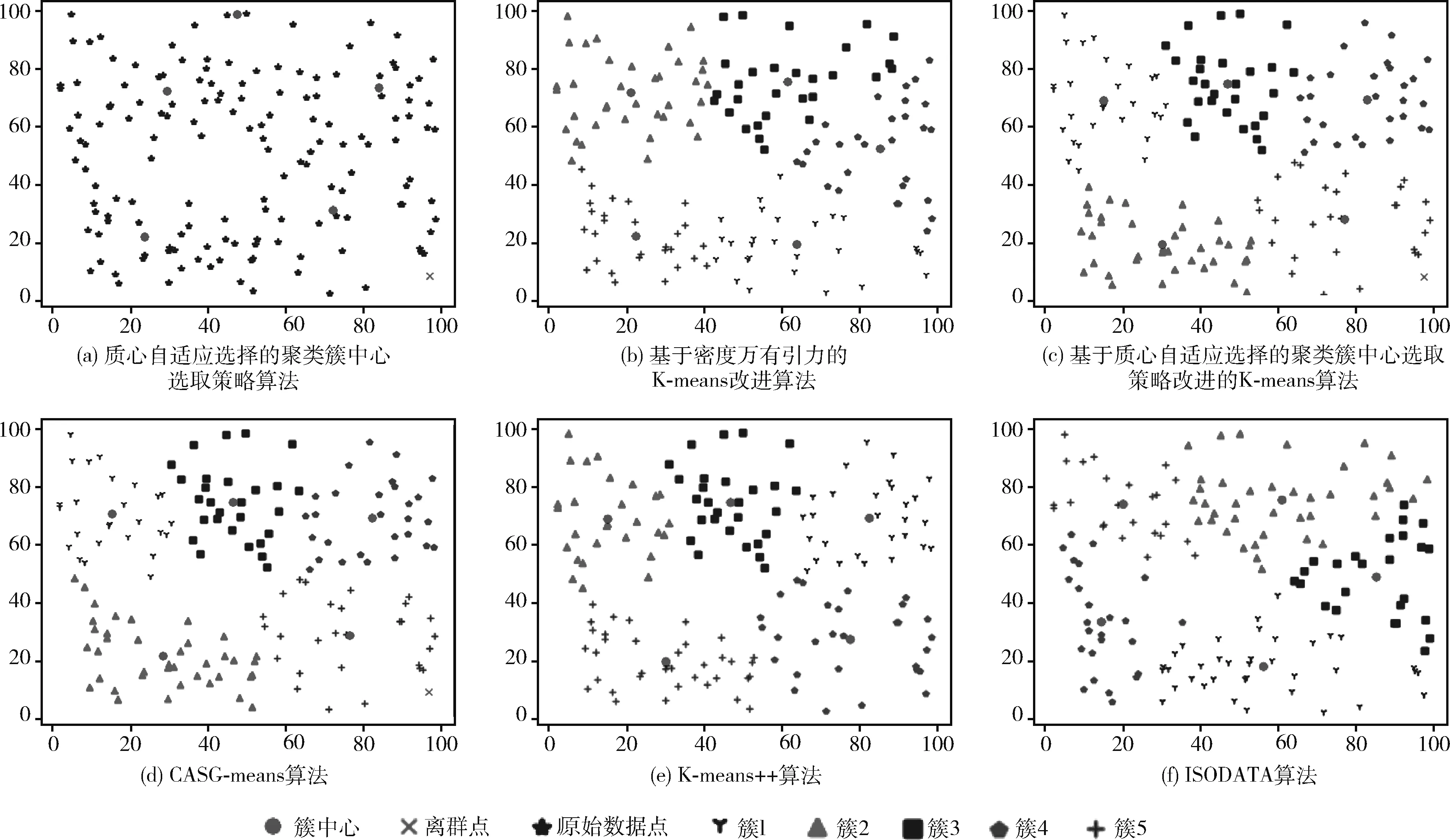
图2 5种算法在数据集1上的对比实验

图3 5种算法在数据集2上的对比实验

图4 5种算法在数据集3上的对比实验

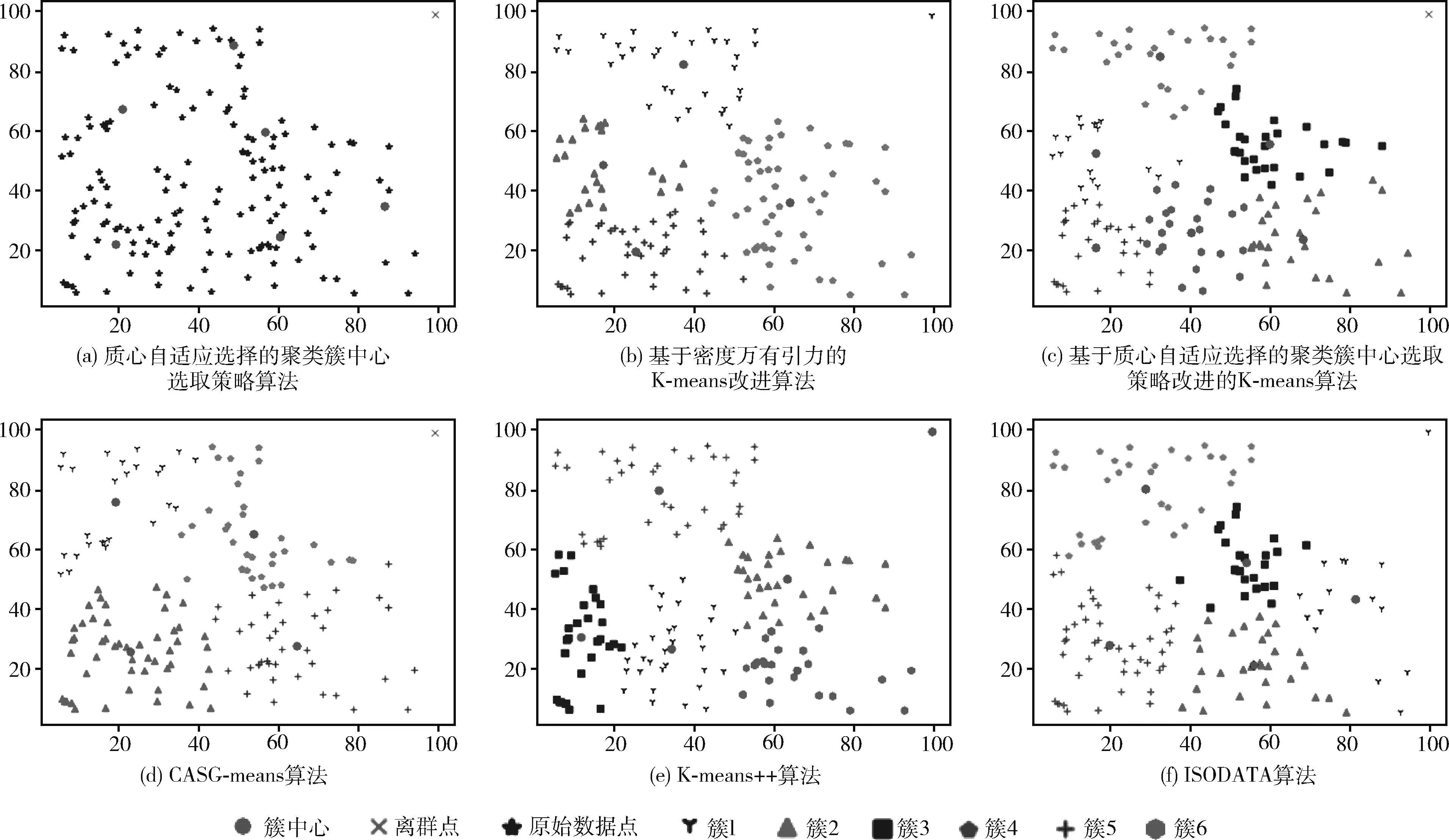
图5 5种算法在数据集4上的对比实验

图6 5种算法在数据集5上的对比实验

数据集1的数据分布的特点是随机均匀分布，对此数据集运行上述5种算法，其实验结果如图2所示。如图2(a)所示，本次选择出来了5个簇中心和1个离群点，本次实验中k=5。 图2(b)的算法①结果图中簇的数目没有减少，迭代次数为16次。图2(c)的算法②结果图中出现了1个离群点，迭代次数为5次。图2(d)的算法③结果图中出现了1个离群点，簇的数目没有减少，迭代次数为5次，算法平均耗时约0.25 μs。图2(e)的算法④结果与图2(d)的算法③结果一致，迭代次数为16次，算法平均耗时约为0.28 μs，算法③比算法④的平均耗时减少了约0.03 μs，迭代次数减少了11次；图2(f)的算法⑤分出了5个簇，与算法③相同，但是由于中迭代次数很小，导致算法运行不充分，部分簇中的点并没有完全划分到理想的簇中，导致存在一些簇的边缘点距离自身簇较远，但是距离其它簇更近。

数据集2的数据分布特点是一半密集一半稀疏，但密集程度相差较小，对此数据集运行上述5种算法其实验结果如图3所示。如图3(a)所示，本次选择出来了6个簇中心，没有离群点，本次实验中k=6。 图3(b)的算法①结果图中簇的数目减少了1个，迭代次数为12次。图3(c)的算法②结果图中没有出现离群点，迭代次数为16次。图3(d)的算法③结果图中簇的数目减少了1个，没有出现离群点，迭代次数为6次，算法平均耗时约为0.275 μs。图3(e)的算法④迭代次数为25次，算法平均耗时约为0.4 μs，算法③的最终簇数目比算法④少1个，算法平均耗时减少了约0.125 μs，迭代次数减少了19次；图3(f)的算法⑤分出了5个簇，相比于一开始给定的k值簇数量减少了1个，与算法③相同，但是随着迭代次数的增加，由于算法⑤的特性，不断进行簇的分裂与合并，簇的数目也在不断发生变化，与算法③相比，算法⑤的结果并不稳定。

数据集3的数据分布特点是中央稀疏边缘密集，但密集程度相差较小，对此数据集运行上述5种算法，其实验结果如图4所示。如图4(a)所示，本次选择出来了5个簇中心和1个离群点，本次实验中k=5。 图4(b)的算法①结果图中簇的数目减少了1个，迭代次数为8次。图4(c)的算法②结果图中出现了1个离群点，迭代次数为10次。图4(d)的算法③结果图中出现了1个离群点，簇数目减少了1个，迭代次数为8次，算法平均耗时约为0.265 μs。图4(e)的算法④迭代次数为10次，算法平均耗时约为0.28 μs，算法③的最终簇数目比算法④少2个，算法平均耗时减少了约0.015 μs，迭代次数减少了2次；图4(f)的算法⑤分出了4个簇，相比于一开始给定的k值簇数量减少了1个，与算法③相同，但是除了簇数目不稳定以外，随着迭代次数增加，簇中心点仍在发生明显移动，说明由于迭代次数较少，算法⑤结果仍然在不断优化中。

数据集4的数据分布特点是均匀分布在其中3个象限中，最后一个象限存在单独一个点，对此数据集运行上述5种算法，其实验结果如图5所示。如图5(a)所示，本次选择出来了6个簇中心和1个离群点，本次实验中k=6。 图5(b)的算法①结果图中簇的数目减少了2个，迭代次数为21次。图5(c)的算法②结果图中出现了1个离群点，迭代次数为29次。图5(d)的算法③结果图中出现了1个离群点，簇的数目减少了2个，迭代次数为14次，算法平均耗时约为0.335 μs。图5(e)的算法④迭代次数为17次，算法平均耗时约为0.405 μs，由于离群点的影响，导致这个离群点成为了一个单独的簇，算法③的最终簇数目比算法④少2个，平均耗时减少了约0.07 μs，迭代次数减少了3次；图5(f)的算法⑤分出了5个簇，相比于一开始给定的k值簇数量减少了1个，比算法③的簇多1个，由于离群点的影响，这个离群点被错误归为了其中的某个簇，并且在算法⑤反复分裂和合并簇的过程中，这个离群点也被反复归为不同的簇，说明离群点对算法⑤的影响大，而算法③一开始将这个点标记为离群点，使得后续迭代过程中不会受到此点的影响。

数据集5的数据分布特点是中央密集边缘稀疏，并且密集程度相查较大，对此数据集运行上述5种算法，其实验结果如图6所示。如图6(a)所示，本次选择出来了7个簇中心和5个离群点，本次实验中k=7。 图6(b)的算法①结果图中簇的数目减少了2个，迭代次数为14次。图6(c)的算法②结果图中出现了5个离群点，迭代次数为24次。图6(d)的算法③结果图中出现了5个离群点，簇数目减少了2个，迭代次数为5次，算法平均耗时约为0.28 μs。图6(e)的算法④迭代次数为23次，算法平均耗时约为0.55 μs，由于离群点的影响，导致这个离群点将其它簇中的点取出，并单独构成了一个簇，算法③的最终簇数目比算法④少2个，平均耗时减少了约0.27 μs，迭代次数减少了18次；图6(f)的算法⑤分出了6个簇，相比于一开始给定的k值簇数量减少了1个，比算法③的簇多1个，由于数据集中心簇的影响，这个簇与其它簇的边缘点在算法⑤反复分裂和合并簇的过程中，反复的发生改变，使得要想得到理想的结果，需要更大的迭代次数，而算法③在引力的吸引下，将中间的簇吸引成为空簇，使得这个簇对聚类的影响效果较小。

通过上述实验对比可以发现，基于密度万有引力的K-means改进算法在可以对部分簇中的点进行吸引，可能形成空簇，从而减少簇的数量，与K-menas算法一样，由于初始点选择不一样，聚类的效果也是不一样的。基于质心自适应选择的聚类簇中心选取策略改进的K-means算法则是在K-means算法的基础上自动根据数据点的分布情况生成簇中心，无需预先给定k值，并且可以识别出离群点。CASG-means算法结合了本文中K-means算法的两种改进思路，同时改进了K-means算法因为k值和初始簇中心选择的不确定性，自动生成了初始簇中心和离群点，并且还结合了引力聚类算法，在过程中自适应调整了簇的数目。而对比现有的较为成熟的改进算法K-means++算法，迭代次数和耗时均有减少，并且可以减少离群点的影响；而对比ISODATA算法，CASG-means算法能在迭代次数较小的情况下获得良好的结果。

3.3 算法迭代次数和离群点、簇数目、耗时减少对比

本次实验在前文所述的30个随机数据集上对普通K-means算法、K-means++算法、ISODATA算法和CASG-means算法做对比实验，在计算普通K-means算法和K-means++算法的迭代次数时，由于这两个算法每次聚类的迭代次数都不同，因此每个数据集上取20次普通K-means算法的平均迭代次数作为本数据集普通K-means算法的迭代次数。

普通K-means算法和CASG-means算法对比实验的结果见表1。通过实验可以得出结论，CASG-means算法相比于普通K-means算法的平均迭代次数减少了5.19次，减少概率为96.67%，簇数目平均减少了1.33个，簇数目减少的概率为63.33%，离群点的平均个数为1.9%，识别出离群点的概率为73.33%。

表1 普通K-means算法和CASG-means算法对比

K-means++算法和CASG-means算法对比实验的结果见表2。通过实验可以得出结论，CASG-means算法相比于K-means++算法的平均迭代次数减少了5.29次，平均耗时减少了0.044 μs。

表2 K-means++算法和CASG-means算法对比

ISODATA算法和CASG-means算法对比实验的结果见表3。通过实验可以得出结论，CASG-means算法相比于ISODATA算法的平均簇数目减少多了0.2个。

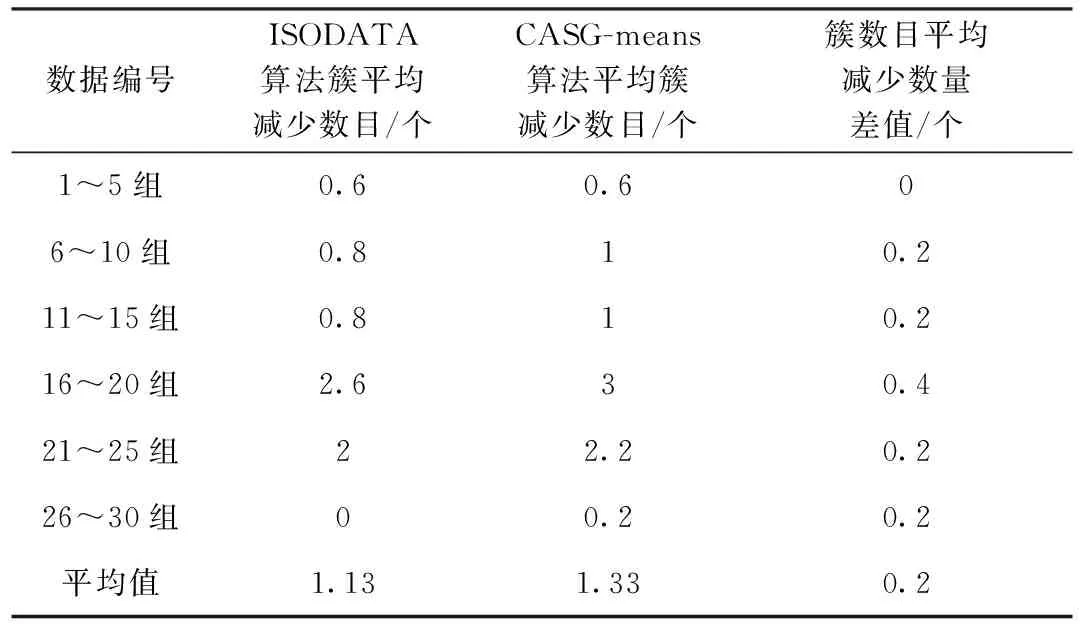
表3 ISODATA算法和CASG-means算法对比

4 结束语

本文提出了一种基于质心自适应选取的密度万有引力聚类(CASG-means)算法，该算法基于以下2点进行改进：①通过质心自适应选择的方法自适应寻找k值和初始簇心点，并判断出离群点；②使用密度万有引力改进公式，代替欧式距离公式，使得各个点之间通过引力相互聚类，并且随着部分簇中的数据点被其它簇全部吸引，最终形成空簇，簇的数量减少，减少了迭代次数。实验结果表明，CASG-means算法相比于普通K-means算法迭代次数平均减少了5.19次，减少概率为96.67%，簇数目平均减少了1.33个，簇数目减少的概率为63.33%，离群点的平均个数为1.9%，识别出离群点的概率为73.33%；CASG-means算法相比于K-means++算法平均迭代次数减少了5.29次，算法平均耗时减少了0.044 μs；CASG-means算法相比于ISODATA算法簇数目平均减少0.2个，因此CASG-means的聚类的效果相比于其它成熟的K-means改进算法更加理想。在未来的研究中，将从算法耗时、离群点识别准确度、密度万有引力公式优化等角度出发对CASG-means算法进行优化。