Thermodynamic assessment of Mg−Ni−Y system focusing on long-period stacking ordered phases in the Mg-rich corner
2022-12-30ChengLiuQunLuoQinFenGuQinLiKuoChihChou
Cheng Liu,Qun Luo,∗,Qin-Fen Gu,Qin Li,∗,Kuo-Chih Chou
a State Key Laboratory of Advanced Special Steels &Shanghai Key Laboratory of Advanced Ferrometallurgy,School of Materials Science and Engineering,Shanghai University,Shanghai 200444,China
b Australian Synchrotron,Clayton 3168,Australia
Abstract The long-period stacking ordered phases (LPSOs) in Mg−Ni−Y system have been attracting great interest as effective strengthening components because of their unique structural characteristics and deformation mechanism.However,the phase relationships in LPSOs are complicated and unclear,which restricts the design of advanced magnesium-based alloys.The aim of the present work is to experimentally determine the phase equilibria relationships focusing on LPSOs and establish the thermodynamic description for Mg−Ni−Y system.Four types of LPSOs,that is,14H,12R,18R and 10H,are confirme through equilibrated alloys and high-resolution transmission electron microscopy (HR-TEM).The formation enthalpies of LPSOs (14H,12R,18R and 10H) are calculated based on density functional theories(DFT) calculations.A new ternary compound,termed as τ phase,is observed for the firs time which is likely to be the distorted structure of 12R as determined from the TEM image which shows a 12-layer closed packing plane distance of 3.252nm and a shear angle of 83.2°between (0002) and (100) planes.Based on the determined phase equilibria relationship,the Mg−Ni−Y system is assessed and a selfconsistent description is obtained where the LPSOs are modeled as the stoichiometric compounds.The comparison between the calculation result and experimental data suggests the accuracy of the present thermodynamic database in the Mg-rich corner.
Keywords: LPSO phases;Crystal structures;Phase equilibria;Thermodynamics.
1.Introduction
Mg-based alloys have been considered as important structural and functional materials in the past decades [1–9].However,the characteristics of poor formability,low absolute strength and slow dehydrogenation kinetics have restricted their practical applications.The long-period stacking ordered phases (LPSOs) are considered as effective phases to solve the above problems.For example,Mg97Zn1RE2alloys containing LPSOs (RE=Y,Gd,Dy,Ho,Er,Tb) exhibit much higher strength than those alloys (RE=La,Ce,Pr,Sm,Nd)without LPSOs [10].The strengthening mechanism was ascribed to the characteristic kink deformation of LPSOs.In addition,the microstructure was refine due to the formation of the kink boundary [11].During the hydrogen absorption/desorption process,the YH2and YH3nano-particles formed owing to the decomposition of LPSOs and enhanced the hydrogen storage kinetics as catalysts[12].Therefore,LPSOs play a critical role in enhancing the structural and functional performance of Mg-based alloys.
Up to date,LPSOs have been reported in the ternary Mg–RE–TM (RE=Y,Gd,Dy,Ho,Er,Tm or Tb;TM=Zn,Cu,Ni or Co) systems [10,13–19].The LPSOs consist of the TM/RE concentrated ABCA-type atom layers,where the TM and RE atoms form TM6RE8clusters.For example,the stacking sequence of 18R can be described as ABACBCBCBACACACBAB.According to the sandwiched Mg atom layers numbers (3,2,1 and 0) by ABCA-type atom layers,the LPSOs can be divided into 14H [20],18R [20],10H [21] and 12R [22,23].Among these alloy systems,many efforts were mainly focused on the Mg−Zn−Y system.As been observed,the density of stacking faults decreases while the density of the precipitates increases when Ni was added into the Mg−3.0wt.%Y−0.5wt.%Zn alloy [24],which is beneficia for the improvement of yield strength of Mg alloys.The substitution of Zn with Ni can also improve the strength of alloys[25] resulting from the increase of the LPSOs’ fraction [26].In addition,the yield strength of 14H is higher than 18R [27].Therefore,it is important to determine the phase equilibria relationship of LPSOs for controlling the types and volume fraction of LPSOs.
Phase diagram is a useful tool for alloy design,but the phase relations in Mg−Ni−Y system are still unclear,especially for the Mg-rich corner containing various LPSOs.Table 1 summarizes the description of different compounds[28–33].Among these ternary phases,the crystal structures of MgNi4Y,Mg2Ni9Y,MgNi2Y2and four types of LPSOs were confirmed while the structures of the rest of the ternary phases remain unknown.The existence of MgNi4Y and Mg2Ni9Y was firstl reported by Kadir et al.[34] and Aona et al.[35].Subsequently,Yao et al.[28] confirme that the MgNi4Y (space groupF3m,a=7.1853nm) and Mg2Ni9Y (space groupRm,a=4.8666nm,c=2.37733nm)were stable phases at 400°C.The MgNi2Y2phase has a tetragonal structure (space groupP4/mbm,a=0.741nm,c=0.373nm) as reported by Hoffmann et al.[36].For LPSOs,the 18R,14H,10H and 12R have been identifie to exist in the Mg-rich region in the Mg−Ni−Y system.Owing to the structural complexity of LPSOs,Kishida et al.[37] determined that the space groups of the most stable structure for 18R,14H and 10H areC2/c,P6322 andCmcebased on the experimental observation and the first-principle calculation.Furthermore,the structure model for the new 12R has been established recently [22,23].The 12R [22] has an original trigonal lattice with parameters ofa=b=1.112nm,c=3.126nm,α=β=90°,γ=120°.Yamashita et al.[23] built the 12R models withR32,C2 andP3121 space group symmetries based on the possible Ni6Y8clusters arrangement and provided the detailed atom positions withR32 symmetry.The development of 12R enriches the family of LPSOs and is useful to understand the structure and formation behaviors of LPSOs.The remaining seven ternary phases,denoted asτ4(Mg5NiY or Mg6NiY)[29,30],τ5(Mg57Ni18Y25)[30],τ6(MgNiY)[29,30],τ8(Mg29Ni20Y42) [29,30],τ9(Mg29.4–30Ni28.1–28.8Y41.6–41.9)[31],τ12(Mg52.4Ni24.2Y23.4) [30] andτ13(Mg8Ni5Y5) [30],were determined to be stable at 400°C [31],but their crystal structures are still unknown.

Table 1 Summary of the ternary phases in the Mg−Ni−Y system.

Table 2 The calculated lattice parameters and formation enthalpies (ΔHf) of LPSOs in the Mg−Ni−Y system.
Because the kinetics of solid-phase transformation is slow[38–40],it is difficul to confir the stable LPSOs at low temperatures.Therefore,the phase relationships for different LPSOs remain controversial.Jiang et al.[32] experimentally determined that two three-phase equilibria of Mg+14H+Mg24Y5and Mg+Mg2Ni+14H existed in the Mgrich region of Mg−Ni−Y system.However,the three-phase equilibrium of 18R+ Mg24Y5+Mg at 400°C was determined in our previous work [33] and Xu et al.’s work [31].Therefore,it is essential to determine where the three-phase region(18R+Mg24Y5+Mg or 14H+Mg24Y5+Mg) exists at 400°C.In addition,there is a dispute concerning the phase equilibria of 10H+MgNi4Y+Mg2Ni or 18R+MgNi4Y+Mg2Ni in the Mg-rich corner [33],because it is impossible for two three-phase regions to coexist in the same isothermal section.Finally,the equilibrium of 10H+Mg24Y5+τ4was reported in Ref.[31] where the composition ofτ4was Mg68.9–74.7Ni10.9–13.1Y12.9–18.1as detected by electron probe microanalysis (EPMA).The composition of this intermetallic compound is close to that of 12R whose crystal structure has been determined asP1 in our previous work [22].Whether an unknown intermetallic compound exists near this composition range needs further experimental investigation.
Limited information can be found in the literature regarding the phase transformation of LPSOs [28,29].Jiang et al.[32] reported that 14H was thermodynamically stable up to 550°C when the alloy composition was located at the Mg+14H phase region and 18R was thermodynamically metastable in the temperature range of 300−500°C[32].The invariant eutectic reaction Liquid→Mg+14H+Mg2Ni occurred at 492°C,which was consistent with the temperature (495.5°C) reported by our previous work [33].However,the experiment results [33] showed that the 18R was stable at 400°C and 500°C.Therefore,the alloy composition located at the Mg+Mg2Ni+14H phase region is chosen to determine whether the 18R is a stable phase or not.
The main purpose of the present work is to determine the phase equilibria relationship for LPSOs including the new type 12R and establish the thermodynamic description of Mg−Ni−Y system through the CALPHAD method [41].
2.Experimental procedures and calculation details
2.1.Experimental procedures
Six ternary alloys were prepared using the original materials: high purity Mg (99.99wt.%),Ni (99.99wt.%) and Y(99.99wt.%) blocks.The Ni−Y alloys were firstl melted at about 1500°C in a medium frequency induction furnace under the protection of ultrahigh purity argon and then cooled down to room temperature in a water-cooled copper crucible.The Ni−Y master alloys and Mg blocks were used to prepare the fina Mg−Ni−Y alloys.The alloys were remelted for fi e times to ensure homogeneity.The fina alloys were weighted to be about 40g.The actual compositions of these alloys were determined by Inductively Coupled Plasma (ICP) as 1#-Mg87.9Ni10.5Y1.6,2#-Mg79.6Ni14.1Y6.3,3#-Mg80.0Ni4.6Y15.4,4#-Mg86.9Ni1.6Y11.5,5#-Mg88.2Ni5.0Y6.8and 6#-Mg90.3Ni4.1Y5.6,respectively.The compositions of alloys were located in the phase regions containing LPSOs.The strips of 3mm×3mm×5mm were cut by wire electrodischarge machine from six ternary alloys ingots.The oxide layers of strips were mechanically removed and then wrapped by the tantalum foil.To prevent oxidation,the strips were sealed in vacuum quartz tubes and then annealed at 375°C for 40 days and at 425°C for 30 days respectively.Finally,they were quenched by an ice–water mixture.The annealing temperatures were selected based on our previous calculation which suggested that a phase transformation would occur at 392°C.After annealing at 425°C for 30 days,the alloys 1#and 6#were annealed for additional 20 days at 425°C to clarify the controversy of the phase relations Mg+Mg2Ni+18R and Mg+Mg2Ni+14H.
The phase constitution was analyzed using X-ray diffraction (XRD) in D8 Advance diffractometer with Cu-Kαradiation.The scanning range was 3° ≤2θ≤80° with a scan rate of 2°/min.The alloys were mechanically ground using SiC papers and then polished using diamond powder (3μm and 1μm).The microstructures of the alloys were characterized on scanning electron microscopy(SEM)JEOL-6700 equipped with an energy dispersive spectrometer (EDS) at an operating voltage 15kV.The samples for TEM observation with a thickness of about 100nm were cut by the FEI-600i focus ion beam (FIB) at an operating voltage 2kV.The selected area electron diffraction (SAED) patterns and TEM images of the samples were obtained from the JEM-2100F TEM at an operating voltage 200kV.
2.2.Thermodynamic models
The Gibbs energies for pure elements Mg,Ni and Y are taken from Scientifi Group Thermodata Europe (SGTE)compilation by Dinsdale [42].The Gibbs free energy of Liquid,Hcp-Mg,Fcc-Ni,Hcp-Y and Bcc-Y are modeled as substitutional-solution phases which Gibbs free energy is written as
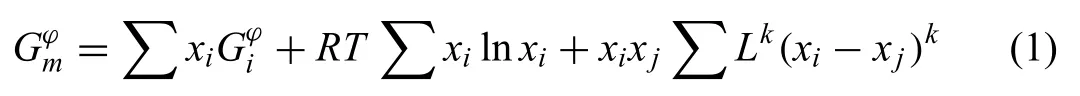
wherexiis the mole fraction of componenti,Gϕ irepresents the Gibbs energy of componentiwith anϕstructure,Ris the gas constant,Tis the absolute temperature,Lkis thekth order interaction coefficient
The Gibbs free energy of the intermetallic compound with little solid solution is modeled as the stoichiometric compound.

where

the ΔGfrepresents the formation energy of the stoichiometric compound.
The Gibbs energy of the intermetallic compound with solid solution of a third element that cannot be neglectable,is modeled by compound energy formalism.

where

i,j,…,krepresents component or vacancy,l,mandqare sublattices,yl irepresents the species concentrations of the componentiin the sublatticel,G(i:j:…:k)is the Gibbs energy of the stoichiometric compound,flrepresents the fraction of sublattice oflin the total lattice sites,Li,j:kvisvth interaction parameters betweeniandjwith themsublattice occupied byk,which is optimized using the experimental phase equilibrium data and thermodynamic property data.
2.3.First-principles calculation details
Owing to the lack of formation enthalpies of LPSOs,the first-principle calculation was used to evaluate the formation enthalpies at 0K.The density functional theories (DFT) calculations for different LPSOs were performed using the Cambridge serial total energy package (CASTEP) [43].The crystal model of 12R with the composition of Mg70.8Ni12.5Y16.7came from our previous TEM results [22].The cell parameters of original structure are:a=b=1.112nm,c=3.126nm,α=β=90°,andγ=120°.Meanwhile,the 12R model withR32 symmetry was also used to calculate the formation enthalpy for accuracy [23].The results [20] show that almost equivalent relaxation takes place for LPSO structures with different RE atoms.Besides,the atomic number of Ni and Zn is close,therefore the LPSO structure in Mg−Ni−Y system is similar to that in Mg−Zn−Y system.The 18R and 14H structure models were from Ref.[20].The simulations of the electron diffraction pattern produced by 18R and 14H models were consistent with the experimental results.The highly ordered 10H model was selected from Ref.[21],in which Zn and Y atoms form short-range ordered Zn6Y8clusters.The generalized gradient approximation (GGA) with the Perdew–Becke–Erzenhof (PBE) parametrization was used for the exchange correlation functional.The cut-off energy was fi ed at 400eV and Monkhorst-Pack k-point mesh of 1×1×1 was used.The structure optimization was going on until the difference of total energy was less than 1×10−4eV/atom,the maximum force on per atom was less than 0.03eV/°A,the maximum stress was less than 0.05GPa,and the maximum displacement between cycles was less than 0.001 °A.
3.Results and discussion
3.1.Thermodynamic stability of LPSOs based on fi st-principles calculations
The crystal lattice parameters of various LPSOs were optimized by DFT calculations and listed in Table 2.Fig.1 shows the comparison of ideal and experimental compositions of different LPSOs and their structures.In LPSOs,Ni and Y atoms are segregated in the local face-centered cubic (ABCA-type close-packed layers),which form the L12–Ni6Y8atom clusters as shown in Fig.1f.Therefore,the atom ratio of Ni/Y of the ideal LPSOs is 3:4.However,the local Ni6Y8clusters are not always fully ordered,in which the Ni and Y atoms can be replaced by the Mg atoms and the center interstitial site can be occupied by Mg atoms [37].The actual compositions of LPSOs are almost along the compositional line with the Ni/Y ratio of 3:4 as shown in Fig.1a.In addition,the numbers of Mg layers sandwiched by the ABCA-type close-packed layers differ according to LPSOs types.The sandwiched Mg atom layers are 3,2,1 and 0 for the 14H,18R,10H and 12R,respectively,as shown in Fig.1b–e.
The total energies of 10H,18R and 14H are calculated to be −11.64×102,−10.00×102and −9.48×102eV/atom shown in Table 2.The total energies of 12R based on different models [22,23] are −9.77×102and −10.91×102eV/atom,respectively.The formation enthalpies ΔHf(LPSO) is expressed by the following equation:
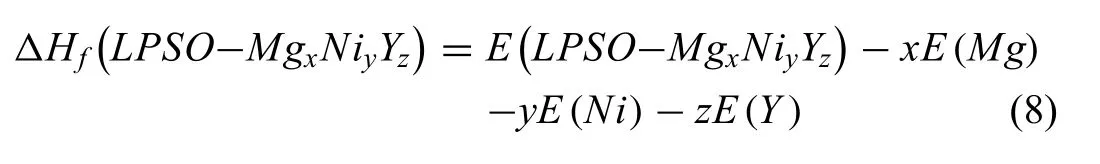
whereE(LPSO-MgxNiyYz),E(Mg),E(Ni),E(Y) represent the energies of LPSO-MgxNiyYz,pure Mg,Ni and Y at 0K,respectively.The calculated formation enthalpies of LPSOs decline with the following sequence: 14H,18R and 10H(−9.14,−9.65 and −11.22kJ/mol atom),which is consistent with that reported from the literature [44–46].The deviation of formation enthalpies is about 1kJ/mol·atom (−9.43 and−10.53kJ/mol atom) based on different 12R models.The effect of deviation on subsequent thermodynamic calculation can be negligible.These calculated data are also used as initial values to optimize the thermodynamic parameters of the Mg−Ni−Y system.
Formation energies are widely used as criteria to evaluate the thermodynamic stability of phases.However,it only considers the competition between pure elements and doesn’t compare the nearby phases.Guo et al.[47] calculated the formation energy and transformation energy of LPSOs in Mg−Zn−Y and Mg−Ni−Y systems,where the stability of LPSOs with convex hulls phases was systematically investigated.Their results showed that 18R is unstable at 0K in both systems and 14H is the most stable phase in both Mg−Zn−Y and Mg−Ni−Y systems.The calculation by Guo et al.[46] considered the interstitial atom Mg in the L12–Ni6Y8clusters,which caused the formation energy difference of the two results.However,the comparison of transformation energy of 14H,18R and 10H in the present work shows that the transformation energy of 14H and 10H are−1.1 and −1.6kJ/mol·atom,while only the transformation energy of 18R is positive (0.3kJ/mol·atom).It suggests that 18R is unstable compared with other LPSOs at 0K,and 14H as well as 10H are stable in this region.
3.2.Phase equilibria of LPSOs
The phase constitutions and microstructures of all alloys were examined by XRD and SEM/EDS.Table 3 summarizes the phase constitutions and chemical compositions of alloys annealed at 375°C and 425°C.

Table 3 Phase constitution and chemical composition of Mg−Ni−Y alloys annealed at 375°C and 425°C.
Fig.2 shows the XRD patterns of the six alloys (1#−6#)annealed at 375°C and 425°C.Based on the crystallographic parameters of LPSOs from Mg−Zn−Y system,the simulated characteristic diffraction peaks of 18R,14H and 10H in Mg−Ni−Y system appear at 5.6°,4.6° and 6.6°,which corresponds to their (0003),(0002) and (0002) close-packed planes,respectively[37].The phase constitutions of alloys 1#,4# and 6# do not change between two temperatures,indicating that no phase transformation for 18R and 14H occurs up to 425°C.
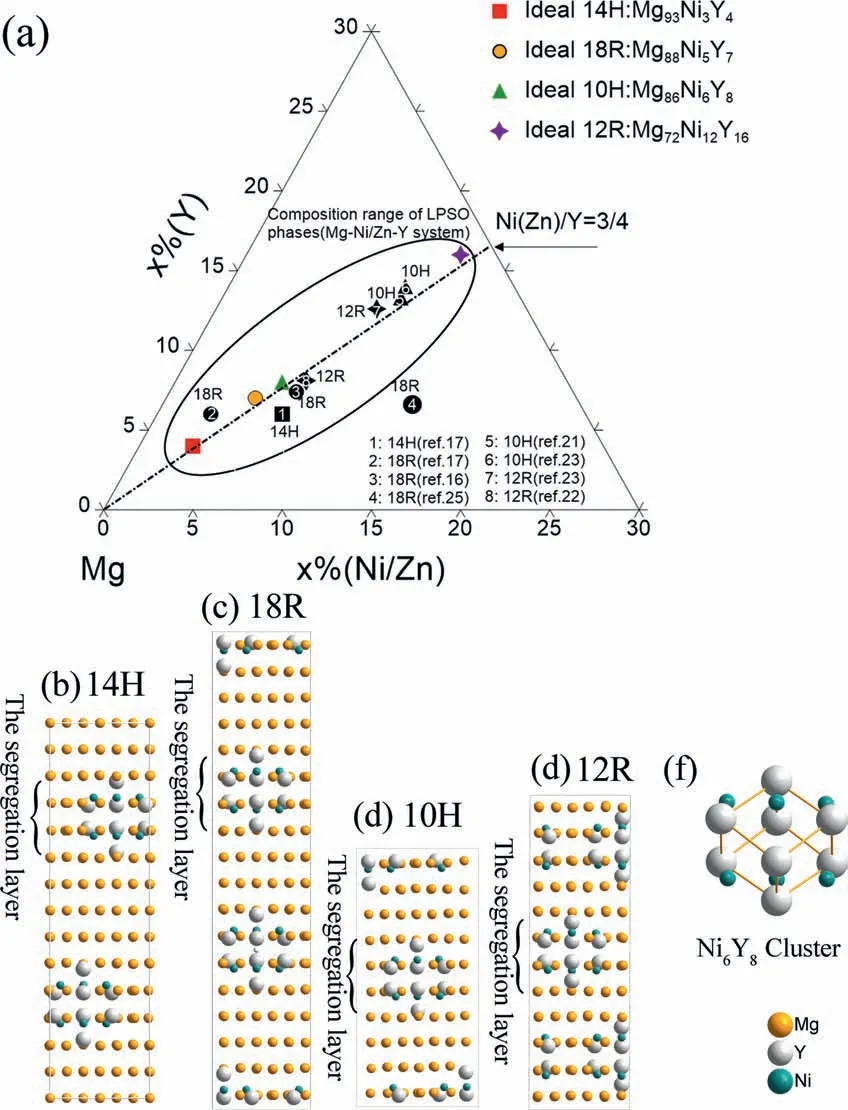
Fig.1.The ideal and actual compositions of LPSOs,experimental data are shown in black points (a),and the relaxed structure of different LPSOs: (b)14H;(c)18R;(d)10H;(e)12R;(f)The local Ni6Y8 atom clusters.
The back-scattered electron images of alloy 1# are shown in Figs.3a and 4a.The microstructure of alloy 1# consists of three different contrast phases: the black dendrite Mg phase,dispersed white strip Mg2Ni phase and gray 14H,which indicates the three-phase equilibrium of Mg+Mg2Ni+14H.However,the equilibrium microstructure of alloy 6# is Mg+Mg2Ni+18R as shown in Figs.3f and 4f: gray 18R,white strip Mg2Ni and black Mg.According to the phase rule,these two-phase equilibria can not exist simultaneously.Only one of the phase equilibria (Mg+Mg2Ni+14H or Mg+Mg2Ni+18R) could exist in the ternary system.The phase equilibrium of Mg+18R+Mg24Y5has been experimentally proved (alloy 4#) and the Mg content of 14H is higher than that of 18R.If the phase equilibrium of Mg+Mg2Ni+18R exists,the 14H will be a metastable phase.If the phase equilibrium of Mg+Mg2Ni+14H is the actual equilibrium,the 18R with low Mg content cannot equilibrate with Mg.
To determine which phase equilibria is stable in this system,the alloys 1# and 6# were annealed at 425°C for additional 20 days (total 50 days).The XRD patterns of alloy 1# and 6# are shown in Fig.5.Fig.6 shows the backscattered electron images of alloys 1# and 6#.The phase equilibria in alloys 1# and 6# are still Mg+Mg2Ni+14H and Mg+Mg2Ni+18R,respectively.It’s difficul to distinguish whether 18R or 14H is stable.Even though the alloys were annealed for a longer time,the actual phase equilibria can’t still be determined.For example,the alloy Mg91Ni4.5Y4.5consists of four phases of Mg,14H,18R and Mg2Ni,which exist even the alloy was annealed at 400°C for 62 days and subsequently at 300°C for further 125 days [32].
The possible reason for the complex situation lies in the small transformation energy of 18R+Mg→14H with only−1.01 meV/atom [47].Besides,in the actual system the composition of 18R and 14H deviates from the ideal composition because of different Ni and Y atoms’occupations in L12clusters.Therefore,it is difficul to determine which phase is stable in the system.Two possible thermodynamic descriptions were provided in Section 3.3.
The XRD pattern of alloy 2#in Fig.2 shows that the alloys are composed of four phases (18R+10H+Mg2Ni+MgNi4Y)at 375°C and three phases (18R+Mg2Ni+MgNi4Y) at 425°C,respectively.The contrast of LPSOs is slightly different as shown in the back-scattered electron (BSE) images(Fig.3b).Combined with EDS results,the center light contrast phase is 10H and the outer dark contrast phase is 18R.However,the 18R+Mg2Ni+MgNi4Y three-phase equilibrium reached at 425°C because of the higher annealing temperature.Therefore,10H is a metastable phase at 375°C.The microstructure of alloy 5# annealed at 375°C consists of white isolated Mg2Ni,gray 18R and light gray 10H in Fig.3f.Because the 10H is a metastable phase at 375°C,the alloy does not reach an equilibrium state.With the increase of annealing temperature,the two-phase equilibrium of Mg2Ni+18R reaches at 425°C as shown in Fig.4f.It indicates that the transformation of 10H to 18R at 375°C is relatively slow.
The slices of 18R and 10H for TEM observation were cut from alloy 5# at 425°C.Five extra diffraction spots are located at 1/6(0002),1/3(0002),1/2(0002),2/3(0002) and 5/6 (0002) positions of Mg taken along [110] direction in Fig.7a.In addition,the diffraction spots on both sides of the central diffraction spots row are asymmetric.The stacking sequence of the closed-packed plane is ABABCACACABCBCBCAB as shown in Fig.7b.The distance of the 18-fold close-packed plane is 4.591nm.The bright atomic columns are enriched in Y and Ni atoms,which form the ABCA-type building blocks.Two layers of Mg atoms are sandwiched by the building blocks.These results indicate the characteristics of the 18R structure.The distance between the central spot and (0002) spots is divided into 10 by the nine extra spots as shown in Fig.7c.The distance of adjacent bright atomic columns containing two-atom layers is 1.473nm,which is fi e times of 0.272nm as shown in Fig.7d.These are the characteristics of 10H,which agrees with the XRD result.

Fig.2.XRD patterns of alloys 1#−6# (a) annealed at 375°C for 40 days and (b) at 425°C for 30days.
Figs.3c and 4c show the microstructures of alloy 3#.The gray phase is 12R,which was reported in the previous work [22].The black phase is Mg24Y5and the white isolated phase is named asτ.Theτis observed for the firs time in this work.Interestingly,the average compositions of 12R andτannealed at 375°C show a slight difference,which are around Mg77.1Ni7.8Y15.1and Mg69.6Ni10.9Y19.5,respectively.The composition of 12R is close to theτ4−Mg68.9–74.7Ni10.9–13.1Y12.9–18.1as reported by Xu et al.[31].Therefore,theτ4phase may be referred as 12R discovered in our work [22].When alloy 3#was annealed at 425°C,the composition of 12R becomes Mg74.4Ni8.4Y17.2,whose Ni and Y contents are higher than that annealed at 375°C and the composition ofτis determined to be Mg70.2Ni9.3Y20.5.When alloy 3# was annealed at 500°C,theτdisappeared and 12R remained [22].This indicated thatτcan transform to 12R with the increase of temperature.

Fig.3.Backscattering SEM images of alloys 1#−6# (labeled as a,b,c,d,e and f) annealed at 375°C for 40 days.

Fig.4.Backscattering SEM images of alloys 1#−6# (labeled as a,b,c,d,e and f) annealed at 425°C for 30 days.
TEM observation were cut from alloy 3# annealed at 375°C.The distinction between the two structures can be easily fig ured out by the means of SAED patterns along [110] direction,as shown in Fig.8.Fig.8b shows the SAED pattern ofτ.Three extra diffraction spots are located at the positions of 1/4(0002)Mg,1/2(0002)Mg,and 3/4(0002)Mg,indicating the 12-fold periodical stacking of the close-packed plane.Compared with the SAED pattern of 12R as shown in Fig.8a,the difference lies in shear angles of (100) and (0002) planes,which are 80.1° and 83.2°,respectively.The calculated shear angle between (100) and (0002) plane is 80.1° with assumed perfect 12R structure (a12R=aMg,c12R=6aMg),which is consistent with the experimental value of the 12R.Theτphase experiences a small lattice distortion compared with 12R.The phenomenon was also observed for 18R in Mg–Co–Y systems[14].The shear angle of 4.8°between(100)and(101)for LPSO-4 is different from that (6.8°) between (100) and(10) for 18R.Even if the deviation is 2°,the LPSO-4 is still recognized as a distorted 18R structure according to the SAED pattern and sequence of the close-packing plane [14].
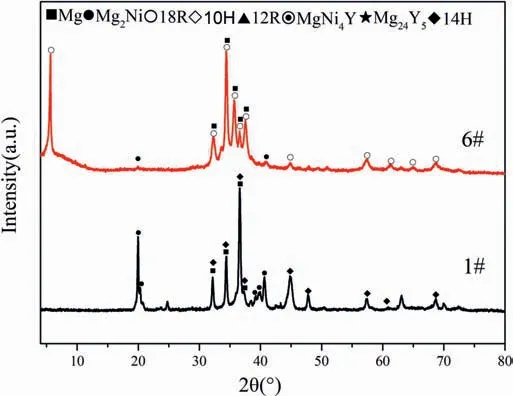
Fig.5.XRD patterns of alloy 1# and 6# annealed at 425°C for 50 days.
Besides,the sequence of close-packing plane of 12R andτphase is the same: ABCACABCBCAB.The distance of 12-fold close-packed planes of theτphase is 3.252nm as shown in Fig.8d,which is close to the distance (3.182nm)of 12R shown in Fig.8c.The lattice parametercof pure magnesium is 0.521nm.When 4wt.% Gd atoms are introduced in the magnesium matrix,thecincreases to 0.527nm.The increased spacing of the (0002) plane is 0.003nm [48].The increased spacing of theτphase and 12R (0002)plane is 0.005nm.Owing to the additional Ni atom solution in theτphase,the increased spacing ofτphase is reasonable compared with 12R.The composition of the 12R andτphase is about Mg73.9–77.1Ni7.8–8.7Y15.1–17.4and Mg68.6–71.2Ni9.3–10.9Y19.5–20.5according to EDS measurement.The composition deviation is only about 2.1 at.% for Y and 0.6 at.% for Ni,which less than the measurement error of EDS (1−5%).The Ni/Y atom ratios are close,that is,0.45−0.58 for 12R and 0.45−0.56 forτphase,respectively.Based on the above analysis,it is inferred thatτphase is the distorted structure of 12R,where the enrichment of Ni and Y elements leads to the distortion and the lattice expansion.Therefore,theτphase is not considered in the following phase diagram assessment.
3.3.Thermodynamic optimization

Fig.6.Backscattering SEM images of alloy 1# and 6# annealed at 425°C for 50 days.
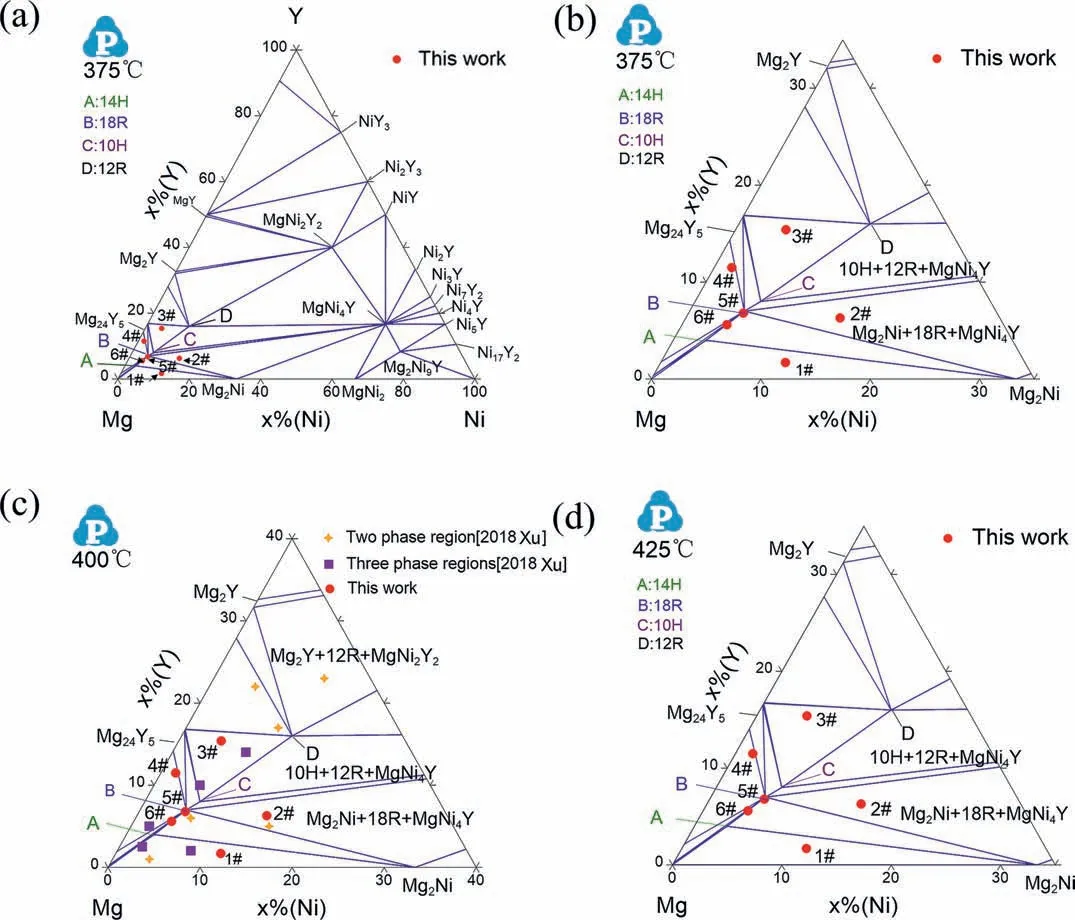
For the thermodynamic description of binary systems,there are two intermetallic compounds,that is,Mg2Ni and MgNi2in Mg−Ni system.The thermodynamic description was firstl obtained by Nayeb-Hashemi and Clark[49].However,the homogeneity range of the MgNi2was not considered.Therefore,Jacobs and Spencer [50] developed a more reliable thermodynamic description of the Mg−Ni system considering a homogeneity range of 0.662 Fig.7.SAED patterns with electron beam parallel to [110] direction from the alloy 5# annealed at 375°C for (a)18R and (c)10H,corresponding HRTEM images for (b)18R and (d) 10H.The HRTEM image for the 18R phase through the autocorrelation by the software Digital Micrograph. The substitutional-solution model is chosen to describe the Liquid,Hcp-Mg,Fcc-Ni,Hcp-Y and Bcc-Y phases.The compound Mg2Ni and nine stable compounds NiAYBare modeled as stoichiometric compounds that exhibit limited solubility of the third element.The MgNi2,MgY,Mg24Y5and Mg2Y phases are modeled by compound energy formalism with two sublattice models.For ternary compounds,the stoichiometric model is chosen to describe the LPSOs,MgNi4Y,Mg2Ni9Y and MgNi2Y2.For the LPSOs of 14H,18R,10H and 12R,the compositions are Mg91Ni4Y5,Mg87Ni5Y8,Mg85Ni6Y9and Mg77Ni8Y15according to their crystal structure and the average value of EDS measurements.The optimization of model parameters and the calculation of phase diagrams were carried out with the Pandat software[57]. Fig.8.SAED patterns with electron beam parallel to [110] direction from the alloy 3# annealed at 375°C for (a) 12R and (b) τ phase,the HRTEM images for the (c) 12R and (d) τphase.The HRTEM image for τphase through the autocorrelation by the software Digital Micrograph. Due to the fact that the phase equilibrium of Mg+Mg2Ni+14H or Mg+Mg2Ni+18R can not be confirme from present experimental results,two sets of thermodynamic descriptions are provided to discuss the phase relations around LPSOs.Assuming that the phase equilibrium of Mg+Mg2Ni+14H is the actual equilibrium,the firs set of thermodynamic parameters are listed in Table 4.The calculated isothermal section of Mg−Ni−Y system at 375°C is shown in Fig.9a.The partial calculated isothermal sections in the Mg-rich region at 375,400 and 425°C are shown in Fig.9b−d.The calculated results are consistent with our experimental results except the uncertain region of Mg+Mg2Ni+14H.Six three-phase equilibria exist around the LPSOs: Mg+Mg2Ni+14H,18R+Mg24Y5+Mg,18R+10H+Mg24Y5,Mg2Ni+18R+MgNi4Y,18R+14H+Mg2Ni,10H+12R+Mg24Y5.It can be confirme that the three-phase region of 18R+Mg24Y5+Mg exists,but not the Mg+14H+Mg24Y5phase region.Finally,owing to the discovery of 12R,the new three-phase region was determined:10H+Mg24Y5+12R,which was also proved from the phase relationship data in alloy Mg78Ni8Y14at 400°C by Xu et al.[31]. Table 4 Optimized thermodynamic parameters in the Mg−Ni−Y system. Table 4(continued) To verify the reliability of the thermodynamic description,the experimental results by Xu et al.[29] are used to compare with the calculated results shown in Fig.9c.The experimental alloys consisting of three phases are located at the calculated three-phase region as shown in purple squares.However,the two-phase alloys are still located at the calculated three-phase region as shown in yellow star plots.This phenomenon results from the small amount of a third phase which makes it difficul to detect the narrow three-phase regions and the composition deviation of alloys. Fig.9.The calculated isothermal sections at (a) 375°C,the calculated isothermal sections of Mg-rich corner at: (b) 375°C,(c) 400°C and (d) 425°C based on the second set of thermodynamic parameters. If 14H is a metastable phase,the 18R can equilibrate with Mg and the phase equilibrium of Mg+18R+Mg2Ni exists.The partial calculated isothermal sections in the Mg-rich region based on the second set of thermodynamic parameters are also consistent with our experimental results at 375°C and 425°C as shown in Fig.10.Compared with calculations of the firs set of parameters,the Mg+Mg2Ni+14H and 18R+14H+Mg2Ni phase regions disappear.The 14H cannot form a stable equilibrium in the Mg-rich corner.However,14H was always observed in Mg−Ni−Y system as reported in different literature [31–33].Therefore,the firs set of thermodynamic description is recommended for further calculation. Fig.10.The calculated isothermal sections of Mg-rich corner at: (a) 375°C and (b) 400°C based on the second set of thermodynamic parameters. Fig.11.The liquidus projection in the Mg-rich corner of the Mg−Ni−Y system based on the firs set of thermodynamic parameters. To explain the formation process of the LPSOs,the liquidus projection in the Mg-rich corner is shown in Fig.11 which is calculated based on the firs set of thermodynamic descriptions.There are nine invariant reactions as shown in Table 5.The calculated results show that four kinds of LPSOs can form directly from the liquid.The 18R transforms into 14H through Liquid+18R→14H+Mg2Ni and into 10H through Liquid+18R→10H+Mg24Y5and Liquid+18R→10H+MgNi4Y.No direct phase transformation occurred between 12R and 10H.The calculated temperature of reaction Liquid→Mg24Y5+Mg+18R is consistent with the experimental result [32].There is a 5°C temperature deviation for the reaction of Liquid→14H+Mg2Ni+Mg from the determined data[33].The 18R,Mg and MgNi4Y phases show large field of primary crystallization on the liquidus surface.However,the 14H has a small fiel of primary crystallization on the liquidus surface,which explains the phenomenon that 18R appeared in most as-cast Mg−Ni−Y alloys in the Mg-rich corner [19,58–60].According to the liquidus projection,the phase composition of as-cast alloys can be predicted through the calculation of solidification The actual primary phases of the alloys in our work and literature are consistent with the predicted results,except for alloy 1#.The composition of alloy 1# is located at the boundary of 18R and MgNi4Y primary phase regions which is very close to the Mg primary phase region. Table 5 The invariant reactions in the Mg-rich corner about the different types of LPSOs.The U,P and E represent quasi-peritectic,peritectic and eutectic reactions. The phase equilibria around LPSOs were investigated systematically and the thermodynamic description of Mg−Ni−Y system was re-optimized based on experimental data.The conclusion can be summarized as follows: (1) The formation enthalpies of 12R,10H,18R and 14H LPSOs were calculated by DFT method.The transformation energy results indicate that 14H and 10H are stable at 0K,but 18R is unstable among those LPSOs. (2) The controversy about the phase equilibria around LPSOs was clarifie by experiments.The phase regions of 18R+MgNi4Y+Mg2Ni and Mg+Mg24Y5+18R are determined.For the new LPSO 12R,a new three-phase region of Mg24Y5+10H+12R is determined. (3) The ternary phaseτwith a composition of 9.3 to 10.9 at.% Ni and 19.5 to 20.5 at.% Y was observed in this work.Based on the comparison of the SEAD pattern with that of 12R,it is inferred thatτphase is the distorted structure of 12R due to the enrichment of Ni and Y atoms. (4) Based on the formation enthalpies and obtained experimental phase equilibria,the Mg−Ni−Y system was assessed using the CALPHAD method.The calculated isothermal sections at 375°C,400°C and 425°C are consistent with the experimental results. Acknowledgments This work was financiall supported by the National Natural Foundation China (51671118 and 51871143),the Science and Technology Committee of Shanghai Municipality(19010500400),the “Chenguang” Program from the Shanghai Municipal Education Commission (17CG42).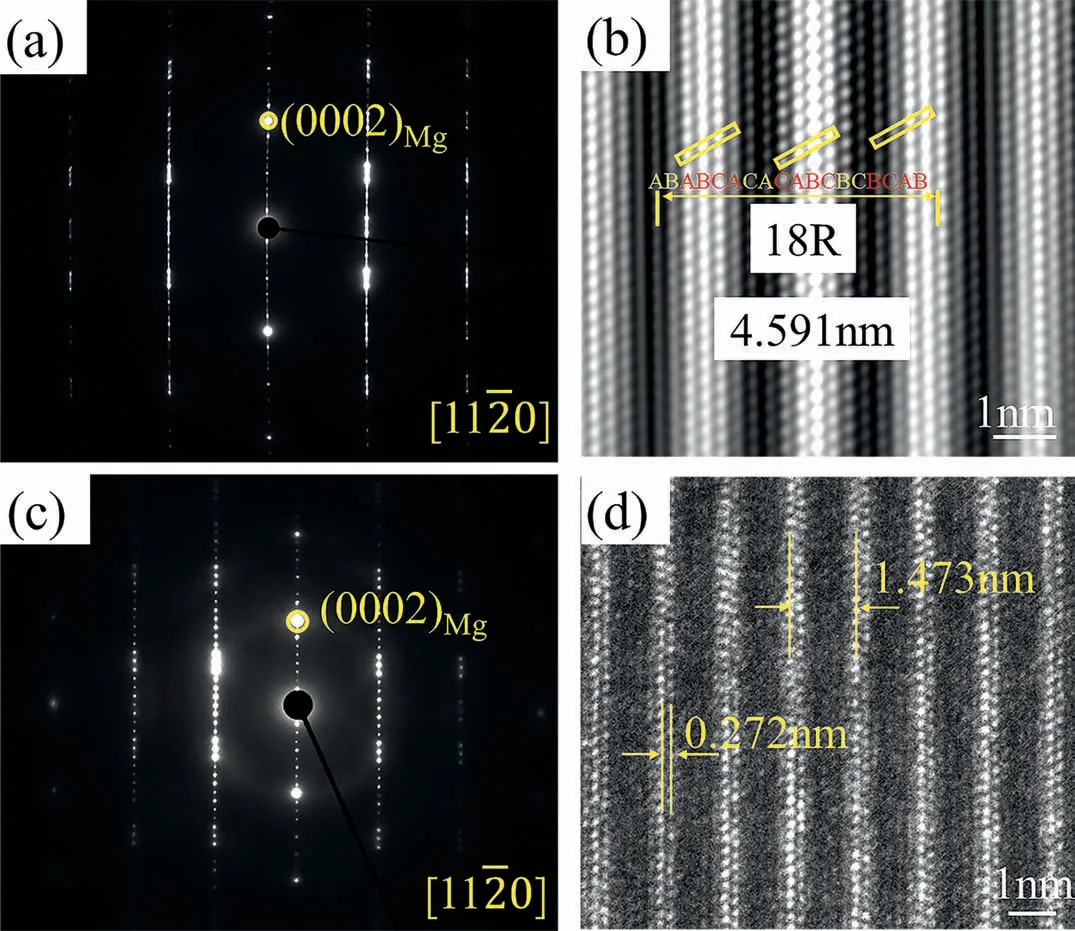





4.Conclusions
杂志排行
Journal of Magnesium and Alloys的其它文章
- Grain refinemen of Mg-alloys by native MgO particles: An overview
- Tailoring MgH2 for hydrogen storage through nanoengineering and catalysis
- In silico studies of magnesium-based implants: A review of the current stage and challenges
- Investigating local corrosion processes of magnesium alloys with scanning probe electrochemical techniques: A review
- A tightly bonded reduced graphene oxide coating on magnesium alloy with photothermal effect for tumor therapy
- Nucleation of recrystallization in magnesium alloy grains of varied orientation and the impacts on texture evolution
