In silico studies of magnesium-based implants: A review of the current stage and challenges

Tamadur Albaraghtheh,Regine Willumeit-Römer,Berit Zeller-Plumhoff

Helmholtz-Zentrum hereon GmbH,Institute of Metallic Biomaterials,Max-Planck-Str.1,Geesthacht 21502,Germany

Abstract In silico methods to study biodegradable implants have recently received increasing attention due to their potential in reducing experimental time and cost.An important application case for in silico methods are magnesium (Mg)-based biodegradable implants,as they represent a powerful alternative to traditional materials used for temporary orthopaedic applications.Controlling Mg alloy degradation is critical to designing an implant that supports the bone healing process.To simulate different aspects of this biodegradation process,several mathematical models have been proposed with the ultimate aim of replacing laboratory experiments with computational modeling.In this review,we provide a comprehensive and critical discussion of the published models and their performance with respect to capturing the complexity of the biodegradation process.This complexity is presented initially.Additionally,the present review discusses the different approaches of optimizing and quantifying the different sources of errors and uncertainties within the proposed models.

Keywords: Biodegradable implants;Degradation; In silico;Phenomenological approach;Physical approach;Validation;Verification Uncertainty quantification Mg.

1.Introduction

Biomedical implants can be traced back to ancient Egypt and South-Central American cultures[1].These implants have been used in different medical applications,from replacing a missing tooth to building up a knee or a hip [1,2].Different biomedical implant materials appear in the literature,i.e.polymers,calcium phosphate,bulk metallic glasses and metals (e.g.titanium,iron and magnesium) [3–5].In the last two decades,innovations in the biomedical fiel played a leading role in increasing the quality,stability and biocompatibility of implants [6].These continuous improvements in the fiel led to a new class of implants made of biodegradable metals,which broke the established paradigm that "metallic biomaterials must be corrosion resistant" [4,7,8].Biodegradable metal implants can be categorized into three classes;magnesium (Mg)-based,iron (Fe)-based and zinc (Zn)-based materials[5,9–11].Biodegradable Mg-based implants are the main focus of this review.

As an element,Mg is one of the lightest engineering metals(density ∼1.7 g) and one of the abundant elements in both earth’s crust and human body [10].Due to these unique properties of Mg,it has been subjected to different applications in different fields for example in transport,energy for medical implants [2,4,12–19].The increased importance of Mgbased implants in orthopaedic applications has been driven by its anti-inflammator ,antibacterial,and osteoinduction properties [20–23].These properties promote Mg-based alloys to be used as short-term implants that will provide the required support during the bone healing process and ultimately dissolve completely in the complex physiological environment of the human body [2,10,17,24].Different types and shapes of Mg-based biomedical implants have been developed to support different types of fractures.The schematic diagram in Fig.1 illustrates some of these biomedical applications for Mg-based implants.

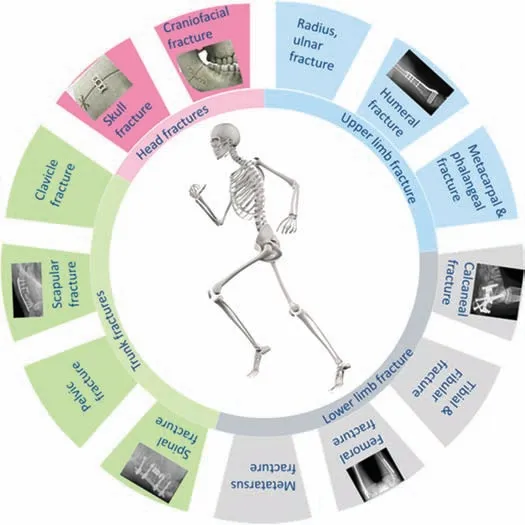
Fig.1.Schematic illustration of different fracture sites in human body requiring various Mg-based biodegradable implants;For head fractious [36],upper limb fractions [37],lower limb fractions [38,39] and trunk fractions[40,41].Fracture classificatio adapted from [25].Skeleton image adapted(under free license from Freepik.com).

The matching degradation kinetics between biodegradable implants and the healing period of biological tissues is one of the key factors for a successful outcome and the degradation must take place with non-harmful residues [4,10,17,25–32].In the development process of biodegradable implants based on Mg,controlling degradation is a challenge.In order to develop a clinically tested implant,severalin vivotests must be conducted.These tests are expensive and time consuming but most importantly they can cause harm and discomfort for the testing subjects.Thus,it is vital to pre-screen the implants throughin vitrotests [27,32,33].In vitrotesting is an effi cient approach to optimize the parameters needed to conductin vivostudies.Furthermore,in vitrodegradation mimics and evaluates specifi subprocesses ofin vivodegradation by series of methods and procedures [10,34].Nevertheless,a gap between the predictions of these studies remains [35].Computational modeling,which is also calledin silicotesting,can be used to fil in this gap,enhance thein vitroandin vivopredictions and speed up the development process.A recent review by Yang et al.[2] highlighted the important role of the mathematical approach in studying the dynamic degradation of Mg-based implants.Computational modeling captures and explains the dynamic physico-chemical interactions that occur in the system and their effects on the morphological and mechanical properties of the implants[2].A key goal of computational modeling is to ultimately create a digital twin that can simulate bothin vivoandin vitrodegradation processes,thus accelerating the material optimization process.However,modeling the degradation process of Mg-based implants is challenging,as it represents a complex multi-scale problem.Consequently,modeling the degradation process of Mg-based implants requires a thorough understanding of the degradation and the factors affecting it.The lack of accurate data to calibrate and optimize a model is another challenge in developing a reliable mathematical framework of degradation.In this regard,it is necessary to validate and verify all developed models through different test scenarios.This review provides a comprehensive overview of the different modeling approaches adopted to model thein vitroandin vivodegradation of magnesium-based biodegradable implants.The models will be reviewed critically in the context of the state-of-theart knowledge on the biodegradation processes.In order to gain a deeper understanding of the system,we will begin by discussing the general concepts of Mg biodegradation and the key factors that affect it.Moreover,we demonstrate the challenges of modeling this complex process and the possible integration of validation and optimization techniques to enhance the development process of models.Finally,we comment on uncertainty quantificatio (UQ) methods and techniques,which are pivotal to yield reliable predictive models in the future.

2.Degradation of biodegradable Mg-based implants

High degradation rates of Mg and its alloys are of major concern when assessing their applicability as implant materials [10,17,25,27–33,42–45].Uncontrolled degradation of Mgbased implants may lead not only to implant failure but also may be a reason for producing a toxic environment within the body [5,10,20,33,46,47].In principle,uncontrolled degradation could raise the pH value of the implant environment significantl ,which can be toxic for living cells in any biological system [33,48].Moreover,the uncontrolled degradation will produce higher amounts of hydrogen gas than the circulation system of the body can handle,leading an accumulation at the implantation site [5,10,20,27,32,33,49–51].

Various factors were reported to control the complex degradation process of biodegradable Mg-based alloys.In the next section,we will discuss the general concept of the degradation process of Mg-based alloys and the key factors affecting it in physiological media.

2.1.Basic concepts of degradation process

The degradation of Mg in water is an electrochemical reaction,where the overall reaction products are magnesium hydroxide and hydrogen gas,as seen by Eq.(1).This reaction involves anodic (for Mg) and cathodic (for H2O) reactions,as seen in the following reactions:

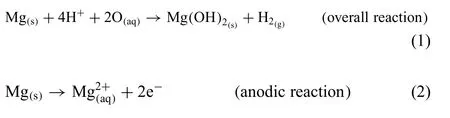
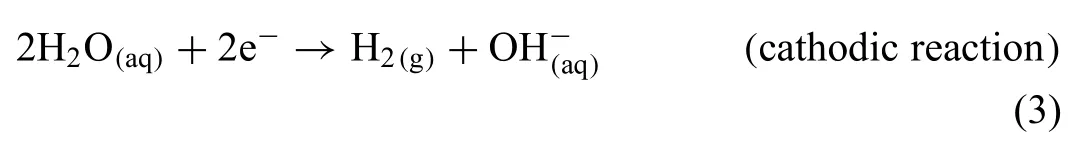
The cathodic reaction in Eq.(3) states that each one mole of Mg degraded is corresponding to the production of one mole of H2[34].Where the overall reaction reflect that the degradation process of Mg is a function of the pH of the system,which means that the dissolution of Mg is depending on the dissolution media.As the pH increases a passive layer of Mg(OH)2will start to form.This protective layer will increase the corrosion resistance of the metal [30,33,52–55].But this layer is only stable under highly alkaline conditions(pH>11),and loses its integrity under acidic conditions or in presence of aggressive ions(i.e.chloride,bromide,and sulphate ions),which induce pitting corrosion [33,50,56].A tendency for galvanic corrosion is reported for Mg-based alloys due to the low standard electrode potential of Mg (−2.72 V)compared to other metals [52].

2.2.Key factors affecting the in vitro degradation process

In general,the key factors controlling the degradation behavior of Mg-based implants in physiological media can be summarized as: medium composition,pH,temperature,CO2and O2concentrations,and medium fl w rate,as well as alloying elements and materials processing routes [27,33].The effect of these factors on the degradation process is not straight forward due to the interactions between them.Understanding these interactions is as important as recognizing the role of each individual factor within the degradation process.Fig.2 presents schematic diagrams of thein vitrotest and the key factors affecting its outcome.Fig.2a presents the immersion test of Mg-based implants.In order to control the degradation test,the samples are placed into an incubator under physiological conditions (37 °C,5% CO2,pH of 7.4)(Fig.2b).

2.2.1.The effect of the degradation medium

The degradation medium composition controls the nature of the degradation process and products,and therefore must be selected carefully to obtain comparable results toin vivodegradation tests [27,32].Fig.2d presents a schematic diagram of the effect of media composition over the degradation mechanism of Mg alloy.Different degradation media have been reported for studying the degradation of Mg and its alloys.These can be simple solutions,such as 0.9 wt.% NaCl,or a complex solution,such as Hanks’ balanced salt solution(HBSS),simulated body flui (SBF),phosphate buffered solutions,modifie eagle medium,and Dulbecco’s modifie Eagle medium (DMEM) [11,27,32,10,11,27,35,57,58].Recently,Mei et al.[59],reviewed the most common degradation media used in literature to test biomedical implants and the degradation mechanisms of Mg-based implants therein.A schematic illustration of degradation mechanisms from basic to highly complex is shown in Fig.3.The complexity of degradation media leads to more complex degradation mechanisms.Up to date,no universal medium has been declared to mimicin vivoconditions completely [11,27,35,57,58].

The effect of the medium’s ionic composition.Due to the presence of additional ions in most of the degradation media usedin vitrostudies,the degradation layer or protective fil that forms on the implant surface during degradation can contain several products in addition to Mg(OH)2.Eqs.(4)–(10)list the main products predicted to form [30].The presence of Ca2+ions in particular has been shown to be highly important,as Lamaka et al.[60] reported a decrease of about 60% in the degradation rate when Ca2+ions are added to HBSS,due to the formation of Ca-containing salts Eqs.(8)–((10) [32],as illustrated by Fig.3 (Ringer‘s solution).In this case,the addition of Ca2+ions was associated with a decrease in the near-surface pH during degradation and a corresponding decrease in the degradation rate [48,60].If both s Ca2+and HCO3−ions are present in the degradation medium,calcite formation Eq.(5)) is observed,as shown in Fig.3 (SBF and cell culture).In addition,the presence of anions HCO3−and CO32−have been shown to promote the formation of the precipitation layers of magnesite (Eq.(6)) and nesquehonite (Eq.(7)) [32].Furthermore,the degradation of Mg in SBF medium is inhibited when a concentration of 27 mM or higher of HCO3−is reported within the medium [48,61].In early stages of degradation CO32−ions are found to increase the degradation rate of Mg [48,62,63],while later they lead to the formation of a protective carbonate layer,due to the fact that most carbonate salts are insoluble under aqueous and physiological conditions (solubility constant of 10 × 10−8).Another protective layer is induced by the phosphate ions(Eqs.(8) and ((9)),which is must stable within a pH range of 4–7 [32,48] (Fig.3,PBS and SBF).

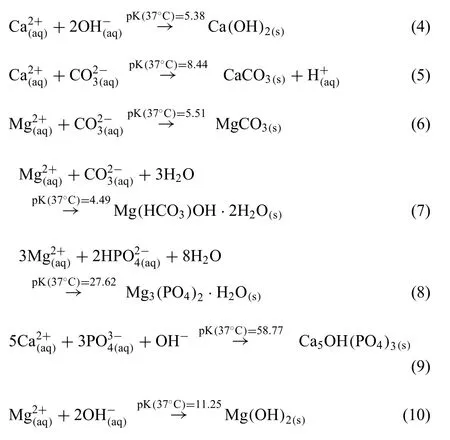
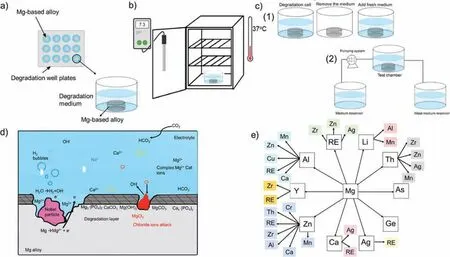
Fig.2.Schematic diagram of the key factors affecting the degradation of Mg-based alloys in physiological media.(a) Schematic diagram in vitro experiment set up.(b) Schematic diagram of controlling the pH and Temperature during the in vitro test within the incubator.(c) Schematic diagram of the hydrodynamic conditions,(1) static and (2) dynamic set in vitro test.(d) Schematic diagram of media composition of the degradation of Mg-based alloys (inspired by [10]).(e) Most reported alloying elements for developing Mg alloys.

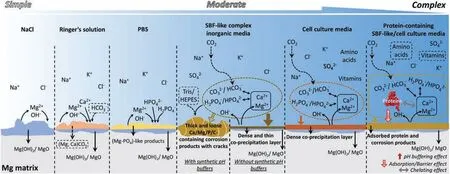
Fig.3.Schematic illustration of the degradation mechanism of Mg in the commonly used media.(adapted with permission from Elsevier [59]).

Another important precipitate that should be considered is the magnesium hydroxide (brucite,Mg(OH)2,Eq.(10)).However,as this layer is stable only in alkaline environment(pH>10),it may not be the main protection during Mgbased implant biodegradation [10,32,60].It was previously shown that the interaction between the different ions present in the degradation medium is very complex and cannot be predicted easily using standard regression analysis or machine leaning approaches [48].

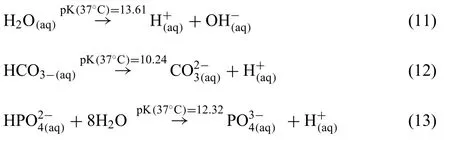
Additionally,the following dissociation reactions of water(Eq.(11)),hydrogen carbonate (Eq.(12)) and hydrogen phosphate (Eq.(13)) need to be considered within physiological solutions.These reactions may change the pH of the medium,thus affecting the chemical equilibrium and the degradation rates [5,32].Eq.(12) in particular depends on the presence of CO2in the atmosphere,which will dissolve to form carbonic acid in water and can then dissociate further.

The effect of organic components.In addition to the ionic composition of the medium,the presence of organic components plays an important role on the degradation process.A comprehensive review by Cai et al.[64],analyzed the effect of bioorganic compounds on the degradation and protection of Mg-based implants to gain a better understanding of how they influenc the degradation process.In this review,the bioorganic molecules (glucose,amino acids,and protein) were shown to play a crucial role in the degradation behavior,mechanism,biomineralization,and surface modificatio of Mg-based implants.Nevertheless,not all experimental work yields a uniform picture.For example,different degradation behavior of high purity (HP)-Mg in the presence of proteins in different degradation medium was reported[65,66]and proteins were found to increase or decrease the degradation rate depending partly on the immersion time and on the alloy [64,65,67].At the same time,other studies reported that proteins have a retardant effect on magnesium degradation and they alter the ion composition of the solutions [65–68].During the degradation process,proteins are adsorbed onto the Mg surface resulting in insoluble layer acting as a barrier against degradation [34,64–66].On the other hand,proteins,in particular bovine serum albumin,amino acids and organic chelating compounds may accelerate or slow the degradation of the implant by forming a complex with the metal cations [60,62,64,67,69,70].Several studies reported that adding albumin to the degradation medium of Mg significantl changes its degradation environment and degradation behavior [71–75].For example,in the early stage of degradation,the degradation rate of HP-Mg in HBSS solution containing fetal bovine serum (FBS) was found to increase.As with proteins,glucose can accelerate or retard the degradation of HP-Mg [62].In saline solutions the transformation of glucose into gluconic acid,which rapidly interacts with the Mg oxides,decreases the pH of the solution,and promotes the absorption of chloride ions on the Mg surface.Due to this,the degradation rate of HP-Mg increases as the glucose content increases in saline solutions [62,76].The opposite to this behavior is reported in Hank’s solution,where the increased glucose content improves the formation of Ca-P compounds on the HP-Mg surface and hence enhances the degradation resistance [34,77].

The effect of pH and pH buffering.To control the environmental conditions pH and temperature,the well plates containing Mg specimen are placed into an incubator,schematic diagram in Fig.2b.Changes in pH shift the precipitation equilibrium during the degradation processes,which directly affects the degradation rate of Mg.The change in the pH of the media may move Mg from being immune to degradation to the degradation phase.Furthermore,the changes in pH directly affect the precipitation of salts within the degradation medium [48,60,78–80].

Based on our previous discussion,it is clear that controlling the pH is a major factor that controls the degradation process of Mg and the production rate of H2gas in the system [32,47,81,82].The degradation process itself of Mg could increase the local pH because of the hydroxide ions produced during the cathodic reaction (Eq.(3)).Due to this the pH of media used in studying the degradation of Mg is controlled using buffer solutions and the CO2buffering system in incubators [10,81].The effect of buffer systems used to regulate test media were highlighted in many studies [27,57,58,61,83].A representative degradation medium should possess the similar buffering capacity to that of blood plasma [27].Low concentrations of phosphate and plasma protein buffers (HPr/Pr) are important to regulate the pH values within the body.Additionally,both HCO3−and CO2are present in the body through the respiration process [27].Gonzalez et al.[27] studied the effect of adjusting the SBF using most common buffers;4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid(HEPES),Tris-HCl,CO2/NaHCO3and phosphate.A different degradation behavior thanin vivostudies was reported under high concentrations of phosphate buffer.HP-Mg degraded four times faster in the presence of HEPES compared to CO2and NaHCO3,because HEPES inhibits the formation of the protective layer by lowering the pH and increases the diffusion of aggressive ions present within the media to the surface of the implant [27,33].A similar effect over pH values was also reported when Tris-HCl was used,due to the fact that Tris-HCl consumes the hydroxide ions formed during the early stages of the degradation process (Eq.(3)) which leads to an increase in the degradation rates[27,61,84].Based on the previous observations,researchers concluded that buffer systems should be carefully selected and only natural buffers should be used in order to reduce their effect on the degradation system.[27,60,69].To clearly understand the interactions of the buffer ions and other ions during the degradation process,the variation of pH between bulk solution and the solution in the vicinity of the Mg surface must be interpreted carefully [48,60].The concentration of CO2in the incubator was found to affect the pH and degradation rate.Note that the pH buffering within physiological medium is obtained by the presence of p(CO2) = 5%.The increased amount of CO2within the degradation media is found to elevate the pH of the system due to the formation of insoluble carbonates and hence suppress the degradation of Mg [48,64,76].

The effect of temperature.In addition to composition and pH of immersion media,the temperature of these fluid affects the degradation process of biodegradable Mg-based implants,Fig.2b.The normal human body temperature is within the range of 36.1–37.2 °C.In comparison to room temperature a temperature of 37 °C will slightly accelerate the degradation process [10,43] as temperature is one of the important factors that affect the solubility of different compounds.It is found for example to affect the precipitation of different calcium phosphates [85].However,studying the effect of temperature over the degradation of Mg-based alloys is not possible without clarifying the connections and interactions between the temperature and other environmental factors,which includes pH and ion concentrations [27].Duringin vitrotests the increased concentration of ions would lead to a slightly elevated temperature,which may affect the degradation rate by increasing the reaction constants [76].

The effect of hydrodynamic conditions.Because the degradation layer of Mg alloys is formed by dissolution-precipitation processes [10],any change in the surface chemistry of the implant will affect the degradation rate and the degradation process in general.Due to this,conducting thein vitrostudies under dynamic or static conditions plays an important role in mimickingin vivostudies.The blood fl w,for example,is one of the complex hydrodynamic conditions that can affect the degradation processin vivostudies.However,this case is not directly expressed within mostin vitrostudies [10,27,86].The presence of hydrodynamic conditions affects the kinetics of the degradation reactions by changing the chemistry of the implant surface.Specificall ,the mass transfer between the implant surface and the surrounding medium will be enhanced,which changes the concentrations of the degradation products,hydroxide ions,local chloride ion and cations by moving them away from the implant site[10,27,86–90].These changes may result in changing the local pH of the implant surface by increasing the fl w-induced shear stress (FISS)[27,42,89].Due to the increased FISS,the deposition of the degradation products may be reduced,thus leading to an acceleration of the degradation of Mg alloys [34,65].In addition,combining FISS and tensile stress was shown to slow the deterioration of strength and even reduce the variation in degradation rate.It is important to note that in this case,tensile stress has a much greater effect than FISS.As the tensile stress increases,degradation rates of Magnesium alloys are accelerated.Additionally,loss of mechanical properties and localized degradation morphology increased with the increase in tensile loading in different degradation media [91].

Mostin vitrostudies are still conducted under static or semi-static conditions [10,27],which means that the mass transfer process between the surface and the bulk medium is controlled by migration and diffusion.In this case,convection may only be present due to the H2evolution from the surface during the cathodic reactions(Eq.(3))[10,27,88].Under dynamic conditions,most reported studies were conducted under laminar fl w with a moderate value of Reynold number(below 1000) [27].Jia et al.[86],conducted dynamic immersion tests under cell culture conditions to investigate surface and internal degradation morphologies,porosity changes and degradation rates of three-dimensional porous Mg scaffolds.In terms of volume loss measurements under dynamic immersion tests,scaffold degradation rates were significantl lower than under semi-static immersion tests for the same system [86,92].Furthermore,the dynamic and statistic conditions were found to affect the adsorption of proteins within the degradation system,which affect the degradation of Mgbased implants.This was recently investigated by Hou et al.[70],where they studied the effect of BSA and FBS in HBSS under static and dynamic conditions.Both BSA and FBS resulted in a slight reduction of degradation rates due to protein adsorption and the formation of Ca/P salts on the top layer of the degradation layer under static conditions,while the reduction in the adsorption of proteins under dynamic conditions lead to a slight acceleration in the degradation rates.

The effect of the volume to area ratio(VA).It is also essential to discuss the volume to area ratio(VA),the implant’s surface area to the immersion medium volume.Researchers reported that this ratio has a significan influenc on degradation rates when it is lower than fi e [48,76,93,94].Low VA ratios can result in a depletion of ions,resulting in the saturation of the medium with certain precipitates [48],with this case being mainly reported under static [27,93,94].Further,controlling the VA ratio is of critical importance in the case of biodegradation of Mg-based implants to avoid changing the bulk pH and hence thein vitrodegradation rates [27].Conversely,the dynamic conditions would accelerate mass transfer between the surface and the bulk solution,resulting in forced participation and a reduction of the limiting diffusion layer.This explains why at the same VA ratio an increase in the FISS will increase the degradation rate under dynamic conditions compared to static conditions [27,91].

2.3.The effect of implant materials

Commercially available pure Mg cannot be used in loadbearing orthopaedic applications,due to its brittle properties,and insufficien corrosion resistance [9,20,49,95].Accordingly,alloying systems are used to tailor these properties [96–99].However,different grain sizes and intermetallic phases present in a Mg alloy,as well as metallic impurities,increase the challenge to understand the behavior of Mg-based implants.Localized degradation is observed within single-phase materials,which leads to pit formation on the surface of the metal [49,52].However,the degradation reactions in aqueous environments are mostly dominated by microgalvanic coupling between magnesium and impurities or secondary phases,which are mostly present at the grain boundaries [49,50,52].

2.3.1.The effect of alloying elements and impurities

In biodegradable implants different alloying metals are introduced [10,100].Fig.2e presents a schematic diagram of the popular alloying elements used in magnesium alloys.The reactions of Mg alloys mainly depend on the alloy chemistry,due to this each Mg-based alloy should be tailored to meet the properties required by the target application position[10,43,101].It was reported that as Mg is alloyed with aluminium(Al)or zirconium(Zr)this will enhance the corrosion resistance.Note that for Al the concentration should be less than 6% in order to enhance both ductility and strength of the alloy [10,43].However,studies showed that Al could cause nerve toxicity and may be related to Alzheimer due to the elevated concentrations of Al3+in the brain [9,20,49,90],thus its use for implant materials should be avoided.When Mg is alloyed with Lithium (Li) it enhances the ductility of the alloy but may reduce the density and the strength of the alloy,which is solved by the ternary alloys with Al,or Mn (manganese) to form Mg-Li-x alloys [10].Higher biocompatibility and enhancement in the bone healing process are clearly noticeable when Mg is alloyed with essential elements of the human body,such as calcium (Ca) and zinc (Zn),Bri.tech Gmbh implants exhibit this characteristic [102,103].Another example for Mg-based alloys is the alloys that contain rare earth elements (REE).The REE-Mg alloys are found to have high biocompatibility and better mechanical properties [20].WE43-based implants (MAGNEZIX) from Syntellix (Hannover,Germany) are available in clinics [104,105].Several published studies try to summarize the different alloying elements and their interactions,for example,summaries can be found in the reviews by Esmaily et al.[10],Chen et al.[9],and Song et al.[55].Besides alloying,the coating of Mg-based implants has been investigated to enhance the mechanical properties and control the degradation process,where various coating techniques and surface modification for the Mg-based implants [10,20,33,49,95,106].

The presence of impurities or intermetallic phases within the system of Mg alloys has been shown to lead to (micro)-galvanic corrosion,which can be accelerated through metallic re-deposition.The galvanic corrosion takes place because of the low electrochemical potential of Mg.The alloying process leads to the presence of two or more metallic phases within the Mg-alloy,which will lead to a difference in the electrochemical potential and hence the Mg will be subjected to anodizing reactions[52,107].Similarly,the presence of impurities such as Fe,Ni or Cu will form micro-galvanic cells,due to the low solubility in Mg.These impurities not only increase the degradation rate of the Mg alloy but also severely effect its mechanical properties [10].The standard theory of anodic dissolution of metals is not able to explain the strong hydrogen evolution reactions (HER) that take place in this case.

In the fiel of biodegradable Mg-based alloys,Höeche et al.[108] conducted a study highlighting this phenomenon within the fiel of the biodegradable Mg-based alloys.They correlated the HER with the electrochemical re-deposition of a thin iron fil on the Mg surface.The re-deposition of Fe is found to accelerate the HER,due to the fact that the HER kinetics itself is strongly dependent on which impurities or the alloying element are present within the system [10,108,109].As the reaction proceeds the re-deposition process becomes the determining process of the degradation system [108].Höeche et al.[108] suggested that the HER kinetics is following the Heyrovsky mechanism,which is the preferred mechanism in an alkaline environment,based on different experimental studies of Mg-Fe systems.Hence the re-deposition mechanism combined with electrochemical desorption according to the Heyrovsky pathway will enhance the hydrogen generation during the degradation process of Mg in the presence of Fe,Ni,and Cu impurities.Based on this,within any system of Mg-based alloys containing Fe,Ni,or Cu,the metallic re-deposition must be restricted in order to control the degradation process[108].However,recent studies by Kokubo and Takadama [58] and Zhang et al.[110] have demonstrated the presence of proteins and organic components as in DMEM+10%FBS increases the threshold at which Fe-impurities become detrimental to the degradation process.As noted in [67],the presumed micro-galvanic corrosion in simulated body flui from impurities in the Mg led to a different degradation morphology,with sub-micrometer sized holes left within the degradation layer.

As a result of these finding and previous discussion,we can see that the degradation process of Mg-based implants is a highly complex multiscale process at thein vitrolevel.The process complexity increases at thein vivolevel due to the presence of additional factors,e.g.the presence of cells,and their complex interactions with the degradation process,as well as varying hydrodynamic and flui properties[25,92,111].Furthermore,differentin vivomodels need to be taken into account when studying degradation processes,such as rats,mice,and sheep [25,111].Detailed experimental results regarding thein vivoandin vitrodegradation behavior and rates of different Mg-based implants were summarized by Bairagi and Mandal [25],where Sekar et al.[111] focused on reviewing the latest development in studying the host response and degradation behavior of Mg-based implants in different animal models and clinical trials.

Understanding these factors and their correlations is crucial to build a reliable mathematical framework.In order to simplify the degradation process,several mathematical approaches appeared in literature,which resulted in having multiple models that are able to describe one or more but not all aspects of the degradation process.In the next section,we are presenting a comprehensive discussion of these approaches and the models derived under their assumptions and hypotheses.

3.Mathematical modeling and simulation studies of Mg-based biodegradable implants degradation

Mathematical models appear in the fiel of metal corrosion as early as the 1950s,mainly by a series of publications by Waber et al.[112–118] in which they provided mathematical representations and analyses of the galvanic corrosion of metals and the key factors affecting the process.Extended computational modeling has been applied to study different corrosion types of metals[119–123]and to predict their behavior under different conditions [124–128].These early models helped in presenting the mathematical approach as a research tool aimed at improving the level of understanding of corrosion processes of metallic systems [119,120,123].However,for biomedical implants,mathematical and computational modeling are relatively new concepts.The complexity of the system,i.e.unclear mechanisms underlying the degradation behavior,precipitate formation,interactions of ions and organic components,is large.Several computational models at both micro- and macroscopic levels have been applied to study the degradation of Mg-based alloys [121,129–135].In the past few years,several researchers have reviewed the computational modeling of the degradation of Mg-based alloys[107,136,137].A review by Boland et al.[136] presented a discussion of the degradation models of Mg-based stents and classifie these models based on the degradation type as uniform,stress,pitting models.In a recent review by Abdallah et al.[107] the models were classifie into phenomenological and physical models based on the basic principle of their derivation,a similar classificatio also proposed in a short review of bioabsorbable Mg-based stents by Zhang and Hao[137].In this work,we are presenting an in-depth critical review of different degradation models developed to simulate thein vitroandin vivodegradation of Mg-based alloys.We elaborate the traditional classificatio of models into physical,phenomenological,analytical and machine learning-based models.Moreover,each of these models is classifie into further subclasses.These subclasses clarify the different aspects covered by each model.Finally,the advantages and limitations of these models are thoroughly discussed.

3.1.Physical approach in modeling Mg degradation

The physical approach in modeling Mg degradation describes the models derived based on the Nernst–Planck equations (NPE).These models are able to capture several interactions within the system,i.e.the migration of ions,the formation of the degradation products and the dissolution reactions.The total flu (Ni,mol·s/m2)of ions in the immersion medium (electrolyte) is described by the NPE [131,138–143]

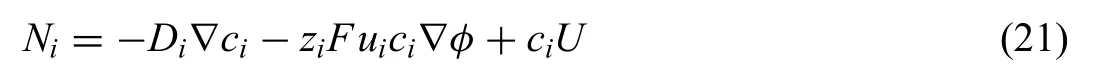
where Diis the diffusion coefficient cidenotes the concentration,ziis the charge,F is Faraday’s constant,U is the electrolyte velocity,andφis the potential.The mobility,ui,is estimated by the Nernst–Einstein equation

here R is the universal gas constant and T is the absolute temperature.Under the assumption of a conserved flu of ionic speciesi,the mass balance of species flu including diffusion and migration at the beginning [131,141] is given by

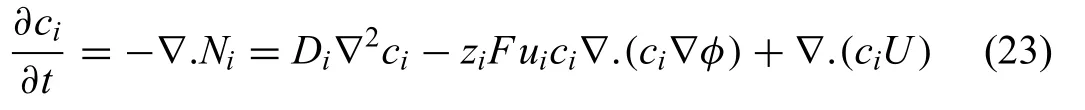
In order to solve the PDE system given in Eq.(23),further assumptions are required for each system.The degradation models derived from the physical approach can be classifie into several subclasses according to assumptions proposed to simplify the PDE in Eq.(23).Several assumption were reported in literature,for example,to simplify the electrochemical reactions only Mg is assumed to be degraded[131,142].Additional assumptions include the neglection of localized degradation,initially assuming a homogeneous surface,assuming that hydrogen bubbles do not react,and that re-dissolution of precipitates does not occur [131,141,144].

3.1.1.Activation controlled models

The activation control models are based on modeling the degradation of Mg-based implant as a function of the potential difference between the anodic Mg and the degradation media.This potential difference leads to accelerating the migration of Mg2+ions from the degradation surface.And at this stage the migration will be faster than the formation of precipitate as presented by the overall degradation reaction (Eq.(1)) [131].

Deshpande [131] applied this approach to study Mg-Al alloy (AM30) system.A well-mixed (no concentration gradients) electroneutral,incompressible immersion medium was assumed.Further,only the degradation of Mg-phase was considered by assuming that the degradation reaction only occurred at the anode surface (Mg-surface,α).Whereas the hydrogen evolution reaction took place at the cathode surface(Al-surface,β).These assumptions reduced Eq.(23) to

Insulation boundary conditions were applied to the electrolyte domain boundaries,presented in Fig.4,to solve the potential Eq.(24).In this case,the degradation rate (DR) was measured as a function of the anode current (ianod) based on Faraday’s law:

where M is the atomic mass of the degraded metal anode,ρis the density,and F is Faraday’s constant (96,485 C/mol).

Bharadwaj and Varadarajan [133] proposed an iterative method to solve the potential equation for a continuously changing computational domain with manually calculated coordinates based on the degradation rate/interface velocity.Deshpande [131] had coupled the model with adaptive meshing to investigate the effect of different metallic phases present.The application of the Arbitrary-Lagrangian-Eulerian (ALE) method enables the model to capture the moving interface during the degradation with high resolution [131,142,145].Thus,Deshpande was able capture the effect of the evolution of cross-sectional microstructure over the micro-galvanic degradation [131].To validate the model,SVET experiments were conducted,where the current density was calculated based on Ohm’s law [131,132].Fig.5 shows that the model was able to predict the spatial current density calculated from the SVET experiments.Both numerical model and SVET experiments indicated that the degradation rate increased as well as the anodic current density.This could be explained by the enhanced degradation activity with the increasedβ-phase fraction.Note that the anodic current density was increased by an order of magnitude as theβ-phase (cathode) increased from 10 to 90%.Also,the model was able to capture the increase in the degradation rate as theβ-phase fraction increased,which was expected due to the increased cathode surface area.The deviation between the model prediction and SVET experiments could be explained by the fact that the model assumed no concentration gradient due to the unrealistic assumption of a well-mixed electrolyte.Also,the solution was assumed to be electroneutral,which is not the case in reality.Adding to that,theβ-phase was not supported in this model,due to that it dissolved in the electrolyte solution as degradation progresses.Further validation of this approach was presented by Deshpande [132] for AE44–mild steel bimetallic couple system,where the degradation rates obtained by the model were within ±7% of the SVET experimental measurements.

Fig.4.The schematic of a computational domain along with the governing equation and the boundary conditions of Deshpande’s model.The Mg-alloy was immersed in the electrolyte with an active exposure length of l.All other boundaries of the electrolyte were assumed to be insulated ∇n∅= 0 (adapted with permission from Elsevier [131]).

Fig.5.The spatial current density variation predicted using the model and estimated from the SVET experiments for different phase fractions: (a) 10% (b)50% and (c) 90%.( adapted with permission from Elsevier [131]).

Under the same assumption and using Eq.(24),Jia et al.[121] investigated the influenc of geometrical factors on the degradation of magnesium AZ91D alloy in contact with mild steel.In this study,the Boundary Element Method (BEM)model predicted a similar distribution of the current density to the experimental measurements.However,the experimentally measured degradation rates were significantl higher.In order to achieve better agreement with experiments,Lacroix et al.[129] studied the galvanic coupling effect of Mg and Al,and calculated both the normal component and the radial component of the current distribution.Furthermore,a concentric geometry of two cylinders was used,which reduced the computational costs of the model.Montoya et al.[146],used this approach in modeling the effect of the electrolyte volume on the corrosion rate of an AZ31 implantin vivo.Based on the spatially explicit model derived here,a proportional relationship emerged between the electrolyte volume and the degradation rate,with a higher degradation rate reported when the implants were covered with a thick layer of electrolyte.The study concluded that the thickness of the electrolyte was one of the key variables in understanding implant degradationin vivo.However,the model did not consider other important factors,such as grain size of the alloy,heat treatment,or the chemical environment and the evolution of hydrogen in the electrolyte,which resulted in the model being restricted to the conditions of the study.Additionally,a quantitative comparison with experimental data was not conducted.

The activation-controlled models were only able to estimate the galvanic current fl w within an order of magnitude compared to the experimental values.Furthermore,these models could not predict the long-term current distribution,nor provide information regarding pitting corrosion[121,129,131,133].These limitations of this subclass of physical models are due to the neglection of the effect of alloy composition,released Mg2+ions,formation and nature of the degradation products,and the composition of the degradation medium.Furthermore,the assumption of stationary anode and cathode surfaces is unrealistic [131,142].

3.1.2.Diffusion-limited models

The second subclass of physical models of Mg alloy degradation are the diffusion-limited models,which are also known as the transport models.Diffusion-limited models assume the diffusion of Mg2+and other ions as the rate-limiting in the transport process.This assumption neglects the influenc of both flui velocity and the migration of ions within the system.As a result,the PDE in Eq.(23) reduces to Fick’s law

The diffusion-limited models also assume that the rates of chemical reactions associated with the degradation process are governed by the transport and solubility of metallic ions in the solution.So,the diffusion of Mg2+ions can be described as:

Grogan et al.[142],applied this approach to study the diffusion process of a pure Mg stent.This model used the moving boundary method to capture the movement of the degradation surface and investigated the degradation of the full stent geometries.However,there were no validation of this model with experimental data,which raised questions over its correctness.Furthermore,the Mg in this system was assumed to have no impurities,which limited the model validity to pure Mgwith limited applicability to real experimental systems.Most applications use Mg-based alloys,which may be subject to micro-galvanic degradation.Also,this assumption created a challenge to track the evolution of the specimen geometry in case of high localized mass loss.

The same model was used by Shen et al.[147] to study the pitting degradation of Mg-1Ca and Mg-3Ge alloys.The parameters of the model were calibrated against the evolved hydrogen from the immersion experiments of a simplifie pin geometry.Only the diffusion of Mg2+ions in SBF was considered and the degradation layer was assumed to compose only of a dense layer of Mg(OH)2.The degradation process was controlled by two main parameters: the diffusivity and the concentrations of Mg2+ions.

To describe the moving interface,both Grogan and Shen used the a formula of the moving boundary velocity derived by Shen et al.and Scheiner and Hellmich[147,148]for pitting corrosion of stainless steel

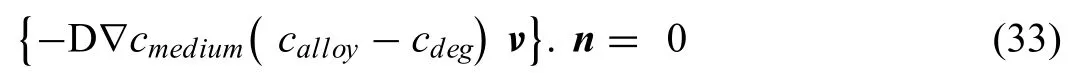
whereνis the velocity of the moving boundaries and the interface normal vector pointing to the degradation layer,is denoted byn.The concentrations of Mg2+ions were measured in the alloy(calloy),within the degradation media(cmedium)and the degradation layer (cdeg,denoted as the saturation concentration by Grogan et al.).

Grogan et al.[142] assumed the presence of a stable layer already covering the stent,note that there was no information about the composition of this layer,it was only used to sustain the assumption of diffusion-controlled degradation.Furthermore,there was no information about the degradation process before the formation of this layer.This limitation was solved later by a further development of the model proposed by Sun et al.[124],which simulated the time-dependent deposition of degradation products on the metal surface by counting the changes in both electrical potential and mass transfer.Sun et al.[124] added the following assumption to this approach: (1) the deposits were porous with constant porosity,(2) there was no re-dissolution of the deposits after precipitation,(3) corrosion deposits are insulating.Based on these assumptions,in addition to being governed by Eq.(23) for mass transfer,the model accounted for electric potential variations according to

whereσis the conductivity of the electrolyte in S/m andυis the relative permittivity.Sun’s model thus included the electric potential of the deposits and the electrolyte in the electrical potential equation.Fig.6 presents the initial current density distributions predicted by this model validated against validation data of SVET experiments [132].

Furthermore,Sun et al.[124] considered the porous nature of the degradation layer,which modifie the diffusion coefficien in the mobility Eq.(22) as

where Dieis the effective diffusion coefficient NMis the Mac-Mullin numberNM=,whereεis the porosity andτis the tortuosity factor of the degradation layer,respectively [149].The outputs of Sun‘s model were in better agreement with experiments than the models presented by Deshpande [131] and Grogan et al.[142].Further development was presented by Bajger et al.[139].Bajger‘s model simulated the formation of the degradation layer in SBF media under physiological conditions.The level set method was implemented to capture the changing geometry of the implants during the degradation process [107,139].HP-Mg with no initial protective layer was assumed.This assumption was justifie in the case of in the case of HP-Mg as a result of the lack of impurities a minimal ion transfer was ensured and the electrochemical degradation was negligible [142].Bajger et al.assumed zero concentration of Mg2+ions and only the presence of Cl−ions in the electrolyte at the beginning of the reaction,based on this assumption the mass transfer in the electrolyte for both ions was measured as

Fig.6.Initial current density distributions predicted by Sun’s model and obtained from the SVET experiments for AE44–mild steel bimetallic(adapted with permission from Springer [124]).

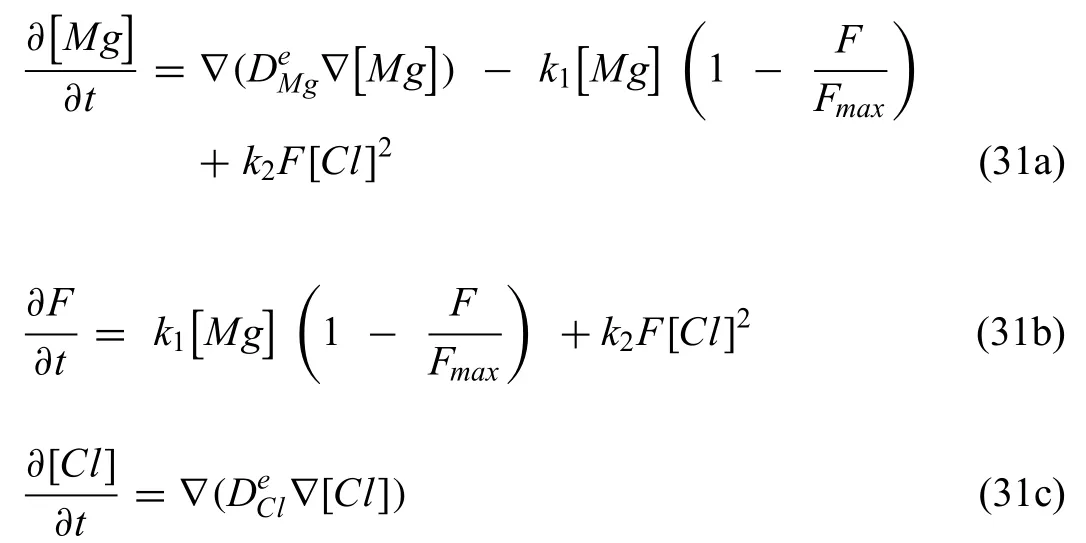
where k1,k2are the reaction rates pertaining to the formation and dissolution of the degradation layer.The model parameters were calibrated against HP-Mg experimental data,where the formation of hydrogen was used to measure the degradation rates.The calibration stage of the model enhanced the ability of the model to predict the degradation layer at different time points during the immersion test as presented in Fig.7.No initial degradation layer at the initial time-step,Fig.7a,where Fig.7b shows that after 7 days a thin degradation layer was formed.However,the degradation layer was assumed uniform and no validation for its thickness was provided.Due to the lack of reported values in literature,the reaction rates were fitte using trial and error to the experimental data,which would increase the uncertainty in the model outcomes.

Recently,Barzegari et al.[150],developed Bajger‘s model for commercially-pure (CP) Mg biomaterials in simulated solutions;NaCl and SBF.The model considered the formation of a protective layer,the effects of the ions in the solution,and the changes in the pH due to the degradation phenomenon.Four scalar functions of space and time were developed to trace the changes in the ion concentrations of Mg2+,chloride Cl−ions and hydroxide OH−ions,as well as the concentration of the protective film which is mainly considered as Mg(OH)2.Added to that,the level set method was implemented to trace the complex interface of the geometry.In order to simulate the pH changes in NaCl and SBF solutions,model parameters were calibrated using a Bayesian optimization algorithm.The model was able to simulate the pH change in NaCl and SBF solutions with an error of 5%.However,a drawback as with previous models arises from the fact that the model calibration was performedviatuning the diffusion rate in Eq.(31a),which does not account for physical phenomena.

Using this approach,Gartzke et al.[101],developed a FE model to investigate the formation of the degradation layer and the change in mechanical properties of the implant duringin vivodegradation.In this model a 3D open-pored structure made of the magnesium alloy LAE442 was adopted to study the change in mechanical properties of the implant during the degradation process.Model calibration data was taken fromin vivoexperiments,where implants were inserted into rabbit femura and analyzed at 6,12,24 and 36 weeks postimplantation.The model was formulated to simulate a homogeneous material with a Mg concentration-dependent Young’s modulus.To track the movement of the interface,the level set method was implemented.The model results regarding the dependence of Young’s modulus on Mg concentration showed good agreement with an empirical solution for cubic opencell foams.The model,however,failed to capture the inhomogeneous degradation behavior observed in the experiment(see Fig.8),as the degradation was based on the diffusion of Mg2+ions only.Further,a number of key factors were not considered,for example,the evolution of hydrogen and the formation of the degradation layer based on the precipitation of different salts based on the chemical environment.

3.1.3.Complex physical models

A more complex physical model was derived by Höche[141].This model investigated the micro-galvanic degradation in a system of Mg coupled to Al.Several chemical reactions were included in this model;i.e.water disassociation(Eq.(11)),which were neglected in the previously presented models.The model further was able to simulate and quantitatively predicted the effect of degradation products on a time-dependent basis.Höche et al.,modifie Eq.(23) to

where Riis the reaction rate of chemical speciesi.Furthermore,the impact of deposit porosity and pH development on the degradation rates were included in the simulations.However,this model assumed that the hydrogen gas bubbles were not interacting in the system,which was a challenge for the overall assumption of a non-degraded cathode.This would mean that the deposits were not affected by the gas bubbles.Also,the effects of gas dissolution in the electrolyte solution were neglected.Static conditions were assumed,which is not the case forin vitrotesting of biomedical implants.The model also assumed that there were no localized corrosion effects,but it included some electrolyte species which would be responsible for the pitting degradation in the system.The model predictions were found in a good agreement with the validation experimental data.

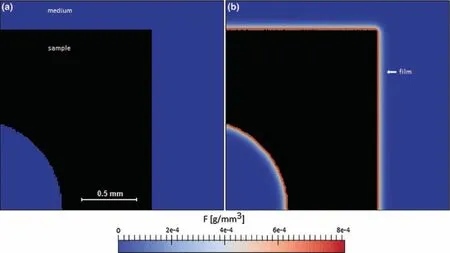
Fig.7.The formation of a thin degradation layer predicted by the Bajger‘s model.(a) t = 0 days of immersion no degradation layer,(b) thin degradation layer after t = 7 days of immersion.(adapted from [139] under a CC-BY-4.0 license).

Fig.8.FE model(left)and experimental results(right)of in vivo degradation on the implant structure at 8 weeks (simulation) and 6 weeks (μCT image)(adapted from [101] under a CC-BY-4.0 license).

Another complex model was introduced by Sanz-Herrera et al.[151] to simulate the effect of multiple chemical species on thein vitrodegradation of Mg-based implant the model included a set of seven species;Mg (metal),H2,H2O,Cl−,MgO2H2and MgCl2.Fick’s law (Eq.(26)) was used to predict the concentration gradient of each of these species.The current model was able to capture the trend of Mg degradation in calibration experiments but required different calibrations for every set of experimental data used.This model was calibrated to slow (0.05 mm/year) and fast degrading samples from the literature (0.3 mm/year),but no error metric was presented to compare model results to the literature.While the model included more ionic species than other models,it failed to incorporate the multitude of ionic species present in body fluids Furthermore,this model was tested forin vivoapplication,where it was used to simulate the degradation of Mg-Zn-Zr screws implanted in Japanese white rabbits.The degradation process was determined by fittin the model key parameters,diffusion rate constant (D) and kinetic constant(kd),to different scenarios ofin vivodata,with the conclusion that the kinetic ratios influence degradation rather than species diffusion.Note that the different fittin scenarios of the parameters reflecte a ratio of four times faster degradationin vivo,however,the results for thein vivocase were fitte based only on a rough visual agreement of the degraded implant.Importantly,this model considered the pH evolution and hydrogen production,which are important factors not only for the degradation but also for the activity of the surrounding tissues.However,no comparison to experimental data was shown for these quantities and only a small number of relevant ions was included in the model.Therefore,while the presented model made an important step towards including some of the physico-chemical interactions in the system,it still contained a number of shortcomings when considering the biodegradation of Mg implants.

Recently,Zeller-Plumhoff and Albaraghtheh et al.[152],developed a model that included all species pertaining to the reactions in Eqs.(4)–(10),as well as dissociation equations.This model simulated the degradation of pure Mg (99.92–99.95%) in SBF over four weeks and under semi-static immersion test.Data from weight loss and volume loss measurements was used to calibrate the degradation model.However,while the NPE was used to describe ion transport,the degradation rate itself was modeled using a data-derived equation.An error of 7% was reported for the simulation results of the anodic dissolution related degradation process of pure Mg in SBF.For the firs time,the model presented a comparison to the literature of simulated precipitate formation,which was calibrated using data from energy-dispersive X-ray spectroscopy (EDX),as shown in Fig.9.

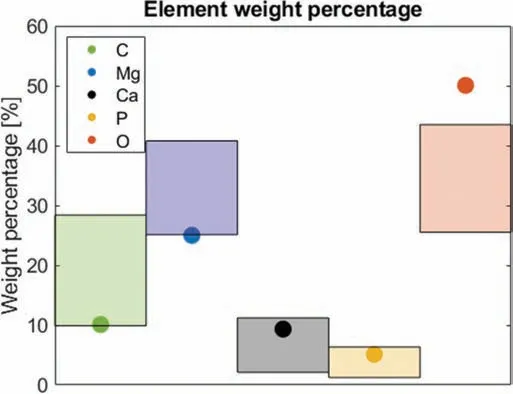
Fig.9.The mean element weight percentages (wt.%) of elements in the degradation layer calculated based on the simulation and measurements using EDX.The scatter points are the predicted weight percentage from the simulation,while the shaded areas indicate the minimum and maximum mean values from the experiment(replotted from[152]under a CC-BY-4.0 license).

Marvi-Mashhadi et al.[153],presented a simulation strategy to simulate the pitting degradation and the mechanical properties of WE43 scaffolds manufactured by laser power bed fusion after immersion in SBF.The strategy presented a phenomenological,diffusion-based model.The diffusion was modeled using FEM,where the values of the diffusion flu were randomly assigned based on the Weibull distribution.The Weibull distribution depends on two parameters:βdetermines the average degradation rate whileγcontrols the degree of localization of degradation,i.e.the lower values ofγwould reflec higher pit formation.The values ofβandγshould be calibrated for each alloy and immersion environment,to defin all the electrochemical and microstructural factors (pH,alloy composition,precipitates,etc.).The diffusion model was validated with X-ray computed tomography results of WE43 alloys immersed in SBF at different times.The geometric elements with a Mg concentration of less than 40% were considered forming precipitates (Mg(OH)2) and were excluded from further mechanical simulations.The phenomenological part of the model was able to predict the reduction in the WE34 scaffold strength due to the progressive change in the deformation mechanisms with the immersion time.Overall,the simulation strategy was able to assess the effect of corrosion on the mechanical behavior of biodegradable scaffolds,which is critical for the design of biodegradable scaffolds for biomedical applications.

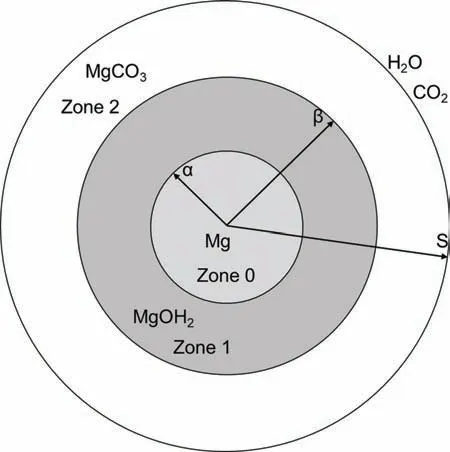
Fig.10.Schematic diagram of triphasic model presented by Ahmed et al.[140], α, β and S are the interface distances of the different phases (redrawn from [140]).

3.1.4.Simplifie physical models

The physical approach is a well-established framework,but the need to update the domain of the system and the requirement for boundary tracking methods increases the complexity and computational costs of this approach.To reduce the complexity of the physical approach researchers have proposed simplifie models.These models were simplifie from computational and mathematical points of view but kept the physical principles of the physical approach.For example;Ahmed et al.[140]developed an advection-diffusion model of Mg-based alloy degradation in an aqueous environment with multiple moving boundaries to investigate the initial degradation process of pure Mg pellets.The simplifie model was built by integrating triphasic models,which enabled the dimensionless presentation of different model parameters,which reduced the mathematical complexity of the model.Moreover,dimensionless studies were known to highlight the true effect of each parameter within the model.Despite the simplificatio of the model,the model was able to demonstrate the effect of different chemical species over thein vitrodegradation of Mg.Furthermore,the integration of the fl w of liquid phases in porous media enhanced the model’s ability to predict the dynamic change in the amount of Mg and the degradation products over time.The schematic diagram in Fig.10 shows the map of Ahmed et al.model.By using the r as spatial coordinate,Ahmed et al.[140] modeled the initial degradation process as a function of the formulation of Mg(OH)2in zone 1 (the regionαβ) and neglected the presence of other species within the system.Furthermore,the porosity of the layers was neglected to ensure a smooth surface which is not the case observed in experiments.

Since solving the physical model can be computationally expensive,analytical functions can be fitte to the physical model predictions to reduce computation time.Adaptation of this approach was made by Shen et al.[147],where the physical model was solved only for the firs 250 h of degradation.Then,a power function was used to fi the data and the degradation rate was calculated using the formula

where A and B are empirical parameters depending on the type of the alloy and the degradation media.In the case of Mg-1Ca alloy pin immersed in SBF solution,A had a value of 0.00198,whereBequaled 0.52207.Where for Mg-3Ge alloy pin immersed in Hanks solution a value was 0.00011 and B was 0.98172.The integration of empirical fittin parameters enhanced the agreement with the experimental data for Shen et al.[147].A similar approach was taken by Grogan et al.[142],who fitte the mass loss usingwith t the degradation time,D the diffusivity,csatthe saturation concentration of Mg2+ions in the medium andα,βfittin parameters.

Dahms et al.[154] immediately derived an analytical model based on the mass conservation law,which was considered a simple two-phase analytical model.The aim of this model was to predict the long-time degradation of Mg-0.3Ca implant material in define physiological electrolyte environments.The model described the mean degradation depthviathe analytical formula

here,h is the mean degradation depth obtainedviafittin from mass loss experiments,h0is the initial degradation depth resulting from the rapid reactions and h∞is the long-time degradation depth.The time-dependent degradation rate DR was measured by differentiating the above equation with respect to time

While empirical models yield good results for fittin the experimental data,their lack of consideration with respect to the electrochemical processes occurring during Mg implant biodegradation limits their application to systems where enough experimental data is already available to calibrate the model empirical parameters.Therefore,predictive modeling cannot be achieved for differing alloy systems or environments.Furthermore,the accuracy of the model would depend directly on the accuracy of the calibration data,due to the use of the best fi method in the calibrations of model parameters.

3.2.Phenomenological approach in modeling of Mg degradation

The phenomenological approach is the second main approach in the modeling of Mg degradation.The models under the phenomenological approach are derived and developed based on the continuum damage theory (CD),which was introduced to calculate the effective stress in geometries with internal discontinuities [155–157].The mathematical description of the degradation process under this approach includes the use of empirical models for surface erosion and their associated mass-loss rates,which integrate the description of the mechanical characteristics under multiple mechanical loads [12].The transition between simplifie physical models and phenomenological models is therefore fluid CD theory models the degradation based on the damage evolution formula presented by Amerinatanzi et al.and Wenman et al.[138,158].In general,Amerinatanzi et al.and Wenman et al.define a scalar damage parameterD,which has a value between 0 and 1,which 0 represents a nondamaged,initial geometry,and 1 an element is fully damaged,fully degraded [156,157].According to the literature,two main issues were reported to associated with the phenomenological approach;it is highly sensitive to mesh resolution as well as the calibration ofDrequired experimental data for each test system [144,157,159,160].Nevertheless,phenomenological models provide information on the interactions of implants with the surrounding environment and can be utilized to predict the mechanical functionality of implants under different conditions of physiological loading [2,107,156].Due to this,models derived under the phenomenological approach are used in the optimization of manufacturing processes,material design and fabrication techniques of Mg-based alloys[12,142].

3.2.1.Uniform,pitting and stress cracks models

The damage evolution formula to reflec the status of the internal geometry over time for uniform degradation is

A CD model of Mg-based stent degradation was proposed by Gastaldi et al.[157],where the stent was assumed to experience two degradation mechanisms: the linear superposition of stress corrosion and uniform micro-galvanic corrosion.Gastaldi et al.therefore decomposed the damage parameter into two parts

where DUis the uniform degradation damage and Dscthe stress corrosion damage.In the current model,the rate of evolution of damage factor was modeled as

whereδUand Leare the characteristic dimension and kUis the kinetics of the uniform corrosion process.While the Dscwas assumed to follow the damage evolution law assumed for the stress degradation process in stainless-steel models

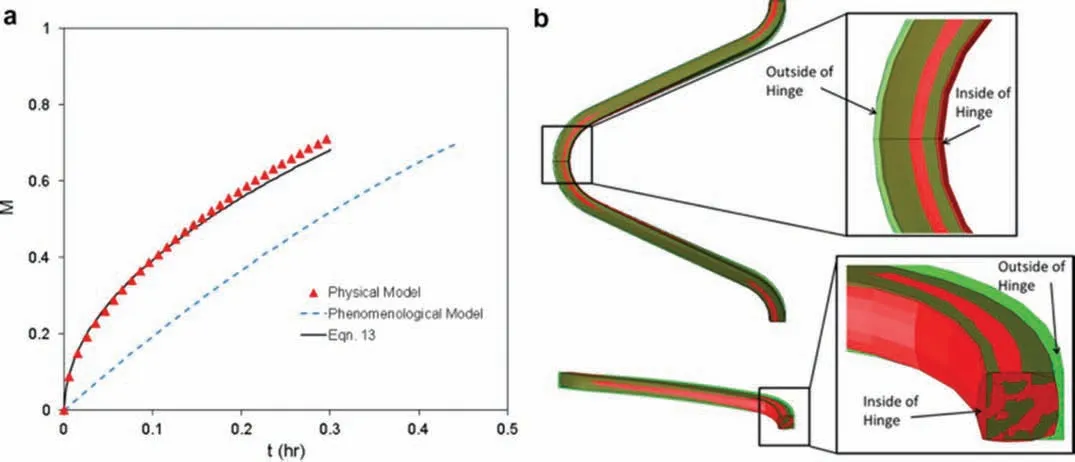
Fig.11.(a) Comparison of percentage of mass loss over time predicted by the degradation models derived by Grogan,the physical model [142],phenomenological model [156] and analytical formula.(b) Comparison of the stent geometry at 70% mass loss for both models.The physical degradation model is shown in red and the phenomenological model is overlaid in transparent green (adapted with permission from Elsevier [142]).

whereσ∗eqis the equivalent stress affecting the entire stress degradation process,σthis the lowest stress value at which the stress degradation occurs.δsis the characteristic length of the stress degradation process,where S and R are parameters related to the degradation media,which are assumed constant over time.In Gastaldi’s modelσthwas assumed to equal half of the yield stress of ZM21 alloy.

The calibration of the model with experiments showed that the developed model reproduced the behavior of different magnesium alloys subjected to static degradation conditions.Gastaldi’s model parameters,S and R were calibrated to simulate the experimental response of uniform and stress degradation experiments and replicated the curve of global damage over degradation time.The model was implemented into an finit element (FE) framework where the damage increment was calculated and hence the degradation of Mg-based stent was measured [157].

Grogan et al.[156]derived a model under the CD approach to study the effect of degradation on the mechanical integrity of stents made of Mg-based alloy (AZ31).The model was able to predict the performance of the stent in an idealized arterial geometry during the degradation process.The use of CD allowed studying the induced micro-scale geometric discontinuities by degradation on overall specimen mechanical integrity without the need for their progression to be explicitly modeled.This was done by introducing the pitting parameterλUto the uniform degradation damage formula as in the following equation

The pitting parameter was randomly assigned to each element of the degradation surface through the use of the Weibull distribution-based random number generator [136,156].All the model parameters were calibrated and quantitatively validated by experiments.However,due to the random location of the pit nucleation,the model could not accurately detect pit location.[136,142,162].

Fig.11 presents a comparison of the two models derived by Grogan et al.,the physical[142]and the phenomenological[156].Both models were tested for the same geometry and under the same conditions.As shown in Fig.11a,differences between the physical model (and the derived analytical formulation) and the phenomenological model can be observed Fig.11b shows that the physical model predicted greater mass loss on the outside of the hinge and less mass loss on the inside of the hinge than the phenomenological model with comparison to the analytical formula derived based on the fittin of the experimental data [142].The observation of non-local mass transfer,due to the pit formation,affected the degradation process and explained the difference in the predicting degradation rates between the physical [142] and the phenomenological [156] models.

Boland et al.[144] implemented Grogan‘s phenomenological model to simulate the localised pitting of a WE43 stent in a joint model of artery remodeling around the stent.The degradation parameters were recalibrated to fi the degradation of a Biotronik Magmaris stent.The aim of this model was to determine the material corrosion rate kU,Weibull function parameterγ,and the growth rate parameter,β.These parameters were validated against independentin vitrodegradation experiments.This simplifie degradation model was considered sufficien to demonstrate the functionality of the biodegradable stent,although it didnot consider the influenc of the biological system on the degradation of the stent,in particular the remodeling of the artery around the stent struts.Moreover,no experimental validation of the model was provided.

3.2.2.Gurson-Tvergaard-Needleman (GTN) model

Vijayaraghavan et al.[123],presented a modifie constitutive material damage model to study the stress corrosion cracking SCC of AZ31 alloy.The Gurson-Tvergaard-Needleman (GTN) model is a modificatio of the CD approach assuming that the damage occurring in the alloy is a result of the formation of the mild cracks and voids on the surface of the alloy under external stresses [123,137].This model can predict the mechanical properties of AZ31 alloy under different temperatures and strain rate.Vijayaraghavan‘s approach provided better predictions of the failure and crack evolution of AZ31 alloys in different degradation media than Grogan‘s CD model.The governing equation of this model was based on the GTN equation [123,137]

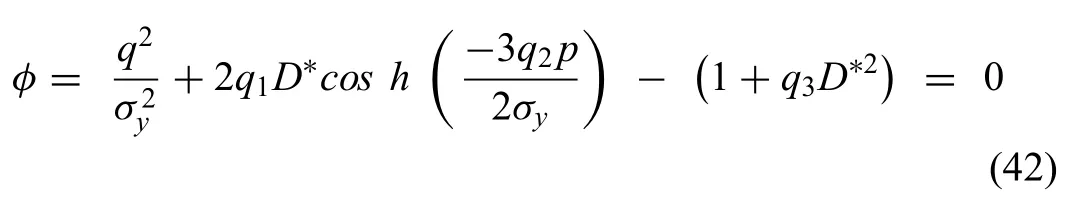
whereσy,p,q are the equivalent,hydrostatic and effective stresses respectively,where q1,q2,and q3are fittin parameters to improve prediction of void interaction effects.The damage parameterD∗was expressed as a function of void volume fractionf,where the normal yield condition equals the GTN yield forD∗= 0 and the alloy fails whenD∗= 1[123].

To overcome the challenges associated with studying both pitting and stress crack degradation,researchers proposed other approaches,like peridynamic (PD),cellular automata(CA) and phase-fiel (PF) models.These approaches have been reviewed by Jafarzadeh et al.[163] for the material science field Prior research suggests that these approaches may be implemented to study the degradation of Mg-based biodegradable implants and may be regarded as a development of the CD approach.

3.3.The cellular automata (CA) approach

The cellular automata (CA) approach has been used in different field like public transport systems,forest fir spreading,biology,ecology and agriculture [163,164].CA models simulate the evolution of multi-phase systems by simulating the behavior and interactions of the individual cell [163,164].In degradation studies,the basic principle of this approach is to reduce the complexity of the system by simplifying the chemical reactions within the system based on the local simplifie heuristics rules of the domain cells.The simplifi cation of the reaction system captures the behavior of the large-scale reaction system based on the local interactions of the cells [164].This reduction in complexity is related to the probabilistic nature of the CA technique,which represents the random properties of the electrochemical degradation reactions.Furthermore,the probabilistic nature of the CA approach eliminates the need for PDE-based mathematical formulation,thus reducing the computational cost [163].CA models contain qualitative presentations of some basic physical and chemical processes [163,164].However,CA models depend on the studied material systems,the rules enforced for the transition process,the determination methods of the CA model parameters and the model dimensions [164–167].

A recent paper by Shahmohmmadi et al.[168],implemented a three-dimensional CA model to study the degradation behavior of Poly-Lactic acid (PLA) and Mg alloy stents.The target of this model was to optimize the volume ratio of Mg within the stent.The optimal design of the stent was obtained by modeling different volume fractions of Mg and the CA model parameters were calibrated against experimental results of 10% of Mg volume fractions.The proposed CA model was able to calculate the degradation rate of Mg in Hank’s buffer solution and to estimate the mechanical properties of the stent.The calibration of the model showed the optimal stent to have 5% of Mg volume fraction.According to the optimized CA model,2.735% of magnesium was degraded after 30 days,whereas 2.716% were degraded in an experiment under the same conditions.

In metal degradation,CA models were found capable of including alloy microstructure in pitting corrosion [169].Furthermore,the rules for the reaction-based restriction were found to obtain realistic looking and stochastic pit morphologies [165].The main advantage of CA models is the simple computational framework that demonstrates the complex degradation system.A number of questions regarding the parametric nature of these models and the absence of quantitative comparisons to experiments remain to be addressed[163–165,167,170].Further,solutions and methodologies are needed to overcome the limitation of the CA model dimensions [163,171,172].This drawback is because the time magnitude and the spatial sizes are not derived based on any physical quantities,thus both require experimental data for calibration for all transition rules [163].

3.4.The peridynamic (PD) approach

The peridynamic(PD)approach is based on a recent theory that provides the possibility to handle material failure in solid structures [163].In solid mechanics,PD models are based on the integrodifferential equations,the solution of these equations includes solving the discontinuities in a solid structure,which is known as fracture and damage [173,174].The PD approach is a further development of the CD approach,where the PD models make use of a characteristic length scale"horizon",which determines the region of the nonlocal interactions.These nonlocal interactions occur between each point in the test domain and its neighborhoods [175].Furthermore,these interactions are controlled with a response function,which includes all the constitutive information of the material [173,174].This means the PD models predictions do not depend on the mesh as is the case in the FE-based models,which reduces the accuracy of the model [176].Due to that,PD models are considered stable and they accurately predict the fracture and crack propagation in solid materials [173,174].The application of this approach in studying the degradation of Mg-based implants may provide a solution to the deviation observed in the predictions between the phenomenological and physical approaches.This assumption could be explained by the fact that the PD approach captures the non-local mass transport,that occurs when the degradation is described by Fick’s law (Eq.(27)) [131,139,142].PD models view the degradation as a type of damage induced in the metal by dissolution,which is coupled with the diffusion problem in the electrolyte [163].This non-local mass transfer was found to affect the degradation process as explained before when explaining the difference between the physical and the phenomenological models presented by Grogan et al.[142,156].

Chen and Bobaru [175] applied the PD approach to study the pitting corrosion damage in Mg-alloys,where only the anodic reaction was modeled as peridynamic diffusion process.Chen and Bobaru [175] coupled the phase-change mechanism to the system to allow the evaluation of the moving interface.This coupling eliminated the need for the flu continuity condition at the interface and allowed autonomous evolution of the moving interface.Furthermore,the complex chemical interactions were contained within the effective diffusion properties.A similar implementation to study the degradationinduced damage in Mg-Zn-Zr (ZK60A) alloy was done by Li et al.[177,178].A diffusion degradation layer was introduced to describe the partial degradation domain and it was differentiated from the degradation product layer.The elemental analysis showed that the composition of the diffusion layer was mainly partially oxidized magnesium and diffused chloride ions.The governing PD equation is given by [175,177]

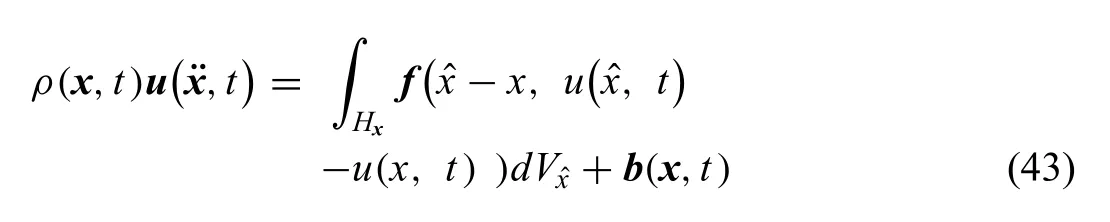
whereρis the mass density,uis the displacement vector field the horizon isHx,fis the pair-wise force function in the peridynamic bond connecting material pointsandxandbis the body density.In the case of ZK60A,the problem was considered as a static problem,which reduced the PD equation into

The energy minimization method was used to solve the PD static problem.The principle of energy minimization method was used to adapt the conjugate gradient method with secant line search,which minimized the energy in the system [177].The above PD models showed that the degradation layer was not easily separable from the bulk,which would increase the initiation of the cracks and the possibility of them propagating into the bulk under external stresses [178].These finding were supported by the experimental studies [177].

Fig.12.Experimental and simulation volume loss for Mg-5Gd and Mg-10Gd,respectively (adapted from [179] under a CC-BY-4.0 license).

In a recent publication,Hermann et al.[179] proposed a computational framework to study thein vitrodegradation of Mg-based biodegradable implants.This framework included two main models;3D PD model to model the degradation of Mg-based alloys and FE model of the residual strength of the implant.The two models were connectedviaa damage variable.The PD degradation model was calibrated to volume loss experiments of Mg-5Gd and Mg-10Gd implants studiedin vitroover the course of 8 weeks,as shown in Fig.12.In this model,an adaptive multi-fine-gri discretization in space and an implicit time-stepping algorithm were implemented to enable the computationally efficien simulation of the complex screw geometry over the entire degradation time.The simulation domain was truncated in close proximity to the implant of interest by introducing non-local Dirichlet absorbing boundary conditions in order to maintain the accuracy of the method.An evolutionary algorithm was used to select non-local kernel functions and calibrate parameters based on volume loss over time experimental data.The model output regarding the residual strength of the implant agreed with experimental observations.

In PD models the propagation of the degradation front does not depend on the discretization as it does for the CA approach.Because the PD theory itself does not require any assumption on the differentiability of the displacement field no special treatments are needed for the displacement fiel due to the presence of crack [176].Furthermore,the presence of the damage-dependent micro-diffusivity coefficien enables the PD models to incorporate different degradation types.Adding to that,PD can be extended to include the chemomechanical models,which enabled the analysis of stressdependent corrosion and stress corrosion cracking [163,180].In PD models,both mechanical and diffusion properties were found to change gradually within the degradation layer,which simulated the actual degradation process.The nonlocality of PD models increased the computational cost of the models because the volume integrals were required to be evaluated at each point in the domain.Parallel computing or the implementation using graphics processing unit-based computing could help in reducing the computational time,but this would increase the complexity of the implementation.Another drawback of the PD models was known as“the PD surface effect”,where the behavior of the model near the boundaries were different than the bulk,which required to apply boundary conditions [163,180].

3.5.The phase-fiel (PF) approach

Phase-fiel (PF) models were implemented to study the degradation of Mg-based implants.These models were applied to evaluate the interfaces between different phases[123].The mathematical formulation of the PF model constructed by applying the Allen–Cahn and Cahn–Hillard equations [181].These equations were coupled to evaluate the phase-fielϕ(X,t),and the concentration field which is also known as the molar concentration of dissolved metal ions c,under the assumption of minimized free energy functionalF(ϕ,c).The form ofF(ϕ,c)depends on the type of degradation system[182].Note that the value ofϕis 1 in one domain and 0 in the other,where over the interface region it will have a value between 0 and 1.The PF models included a length scale due to the presence of the thickness of the interference (l).The material phase of transition described by the Allen-Cahn equation [120,163,181]

whereLis the interference kinetics parameter andδF/δϕis the variational differentiation of the energy functional with respect to the PF variable [182].Cahn-Hilliard equation describes the evolution of the molar concentration of the metal atoms [120,163,181]

whereδF/δcis the variational differentiation of the energy functional with respect to concentration [182].Dis the scalar diffusion mobility and it is a function of the diffusivity of the electrolyte,the free energy functional and the type of degradation.

Ma et al.[181] implemented the PF approach to simulate the impact of the stress assisted degradation of biodegradable Mg alloys with porous microstructures.In this investigation,Mg-based plates with and without pores were simulated.The phase-fiel variableϕwas set to 0 for the electrolyte and 1 for the Mg.The total free energy of the system was given by

whereFelrepresented the elastic strain energy stored in the system.FbulkandFintpresented the electrochemical energy of the bulk phases and the interface energy required for material dissolutions,respectively [181].As shown in Fig.13,the PF model was able to simulate the evolution of the degradation surface during the stress assisted corrosion process of Mgbased alloys.

The mathematical nature of the PF models increases the computational cost of these models.The coupled PDEs introduces a dense mathematical framework to the system.Furthermore,PF models are strongly dependent on the selected free energy function,which would affect the ability of PF models to predict the damage evolution.A transition region was observed within the PF models at the degradation front similar to PD models.But in PF models this layer was found to depend on the selected free-energy function,where as in PD models this layer was found to depend on the nearby conditions around a test point.Due to this,PF models failed to predict the oscillatory behavior in thermally driven cracks but PD models were able to predict this behavior in high detail[183–186].

To summarize the models presented in this review,Table 1 presents a brief overview of the models applied to simulate thein vivoand thein vitrodegradation of Mg-based implants.

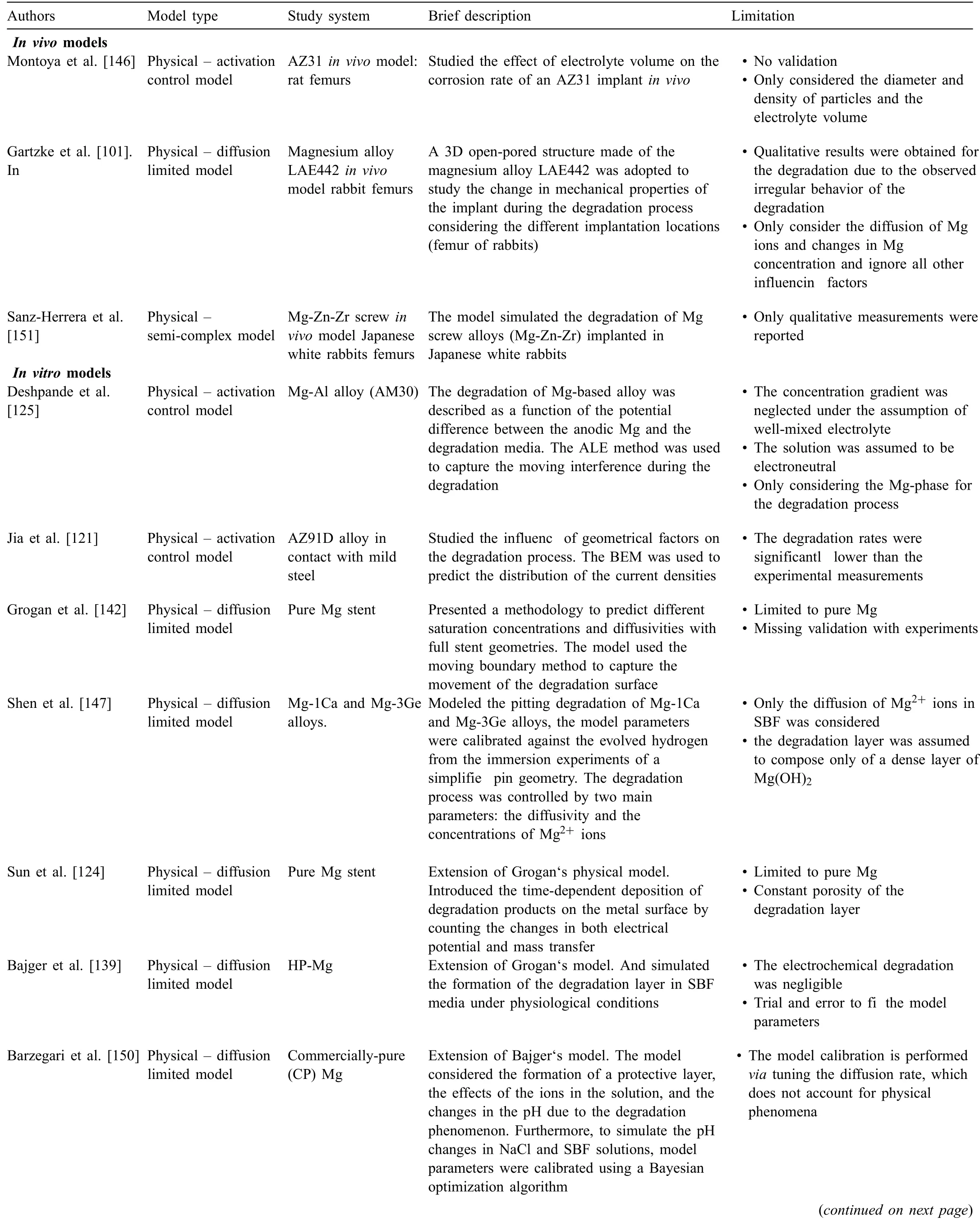
Table 1 Summary of the degradation models of biodegradable Mg-based implants investigated in this review,which were published between 2011 and 2022.

Table 1 (continued)

Despite the important role thatin silicotesting of Mg implants can play in clarifying the overall process and propagation of the degradation process,there is no comprehensive computational framework that can predict the degradation behavior of Mg-based implants in bothin vivoandin vitroenvironments.Each of the discussed approaches was built over several hypotheses and assumptions: simplifie chemistry,considering a limited number of species within the system,simplifie kinetic mechanisms,the electrochemical reactions are simplifie to the basic anodic and cathodic reactions and few complex geometries are used.These simplifie assumptions affect the reliability of the models and in many cases limit the model applicability to a certain system or conditions.Moreover,the lack of understanding and knowledge of the underlying processes of Mg biodegradation need to be improved to arrive at a point where a comprehensive and predictive computational framework for Mg degradation can be derived.Some of these remaining knowledge gaps are related to the degradation process itself,such as the complex mechanisms of the degradation,unclear understanding of the degradation kinetics,the accumulation of H2in the system and the control of the pH [2,10].Additionally,many values for the key parameters of the degradation process,such as reaction rate constants,diffusion coefficient and porosity remain unknown or are difficul to assess experimentally [48,113,136,138,139,141].Furthermore,the degradation process of Mg is a multiscale problem,which increases the complexity of the mathematical representation and will require a multiscale computational framework to enable predictive modeling of the degradation of Mg-based implant[113,135,136,141,144,187].Finally,the model calibration and the selection of the experimental data required for the validation of these models affect their reliability.Thus,these models require further optimization,calibration,and validation.

Fig.13.Evolution of the morphology of the degradation surface at different times for the plates with and without pores (adapted with permission from John Wiley and Sons [181]).

4.Reliability of the in silico approach

Highly informative models of the degradation of Mg-based alloys can only be achieved when the model is representing a digital twin of thein vitroexperiments,which means that the model outputs fi the experimental results qualitatively and quantitatively.Regardless of how comprehensive or accurate the degradation models of Mg-based alloys are,these models are a partial representation of the real system,due to several sources of uncertainties.These uncertainties accumulated within the system from the assumptions and hypothesis,which affect the development process of the model,the model parameters,the discretization techniques,and the experimental data that is used to calibrate and validate the model.To establish reliable models,it is therefore pivotal to identify and quantify the sources of uncertainties and errors in the model.At this stage,calibration,validation and verificatio play a large role.

4.1.Analysis techniques of in vitro studies of the degradation of Mg-based implants

The assess the validity of any degradation model,a comparison with experimental data is required.To this end,different parameters can be assessed,such as mass or volume loss,the potential of the electrolyte or the composition of the degradation layer.The degradation properties in electrochemical tests are evaluated by testing the open circuit potential(OCP),polarization curves and electrochemical impedance spectroscopy (EIS) via a three-electrode system [34,188].In the immersion test,the study samples are immersed in a chemical solution in isolated wells and then either the mass loss or volume loss can be assessed or the degradation products are analyzed by a series of methods [33,34,52].The immersion method is the common testing method for biodegradable materials,where the related testing protocols are published as: ISO 10993-15 (Biological evaluation of medical devices-Part 15: Identificatio and quantificatio of degradation products from metals and alloys) [189] and ASTM G31-72(Standard practice for laboratory immersion corrosion testing of metals) [190].

Different evaluation methods are used in the measurement and analysis of the degradation products,these methods are differing in their nature as physical or chemical tests,destructive or non-destructive for the test samples.Also,they can be categorized into unpolarized and polarized methods.Esmaily et al.[10] presented a comprehensive review over the different analysis techniques and methods that are used to study the degradation of Mg-alloys under different conditions.In this review we shortly summarize the most common methods used to evaluate the degradation rate of Mg alloys that can be used for calibration and validation of computational models.

4.1.1.Hydrogen evolution measurement

The degradation rate of Mg can be measured by measuring the volume of H2evolved,which is generally assumed to be equivalent to the mass loss of Mg (Eq.(1)) [34].The volume of the gas is calculatedviathe gas law

where P is the atmospheric pressure (Pa),V is the volume of H2(m3),n is the substance amount of the gas (mol) and T is the temperature (K).This method is a real-time measurement of degradation with acceptable accuracy of calculating the alkalization in simple NaCl solutions.The measured degradation rate is not affected by the presence of degradation products but also gives no indication for them [34].Consequently,this method gives limited information of the degradation mechanism and it is difficul to run concurrent to polarisation experiments [33].The results of this experiment can be affected by changes in the atmospheric pressure and hydrogen leakage from the set-up [34].Moreover,they are only valid if the oxygen reduction reaction is truly negligible during Mg biodegradation,despite recent evidence to the contrary [59].

4.1.2.pH monitoring

During the degradation of Mg,hydroxide ions are produced by the cathodic reaction (Eq.(3)),where the change in the concentration of OH−will increase the pH of the media[52,83].Measuring pH changes of the system can yield indirect information on the degradation rate of Mg alloys in simple immersion media and the influenc of changing the media or alloying elements on the process[7,102,107,191].pH monitoring is a low cost,easy to perform and continuous method.However,it is not an alternative to other methods,since the pH change will be influence by buffer systems,difference between surface and bulk [59] and there is no quantitative measurement of the degradation rate [7,192].

4.1.3.Potentiodynamic polarization (PDP)

In potentiodynamic polarization,the degradation is studied through measuring the current by applying a single fi ed potential,where the degradation rate is calculated by the formula[10,33].

where K value is 3.273 × 10−3mmg/ (μA cm a),Icorris the current density,and meis the equivalent mass.This method is widely used to study the degradation [10,34,66],due to the relatively easy setup,easy preparation of samples and obtaining a dynamic profil of the degradation process [10].The main disadvantages associated with this method are the requirement of specialized equipment,the need for assumptions of generalized corrosion and the high sensitivity to variations and errors [33].Moreover,polarization measurements may be influence by the dynamic process of the degradation layer formation and organic components may have a negative impact on the electrode behavior due to adsorption on its surface.

4.1.4.Electrochemical impedance spectroscopy

Electrochemical impedance spectroscopy (EIS) is a nondestructive method with a relatively easy setup and simple sample preparation.EIS provides continuous real time measurement and is able to quantify the formation of surface layers and the effect of these layers on the corrosion protection.In case of coating,EIS helps in determining the timedependent breakdown,through calculating the current density of the degradation by Stern-Geary equation [33,107].However,this method lacks the information over anodic/cathodic contribution and it is susceptible to corrosion that occurs over a period of time [10,33].

4.1.5.Mass loss

The mass loss method is based on measuring the change in the mass of the sample before and after the immersion test.To this end,the degradation layer that may form on the sample surface must be removed using chromic acid treatment [5,34].Mass loss is an unpolarised method,where the degradation rate is calculated using the following formula [34]

where DR is the degradation rate,ΔWis the change in the weight,A is the original surface area and t is the exposure time.This method is low cost,simple to set up and perform.It is also easy to control the test environment.Furthermore,the output of these methods are accurate and clearly define and concurrent polarization experiments are possible [33,34].The main disadvantages of this method are the lack of information about the degradation mechanism,the absence of time-dependent degradation behavior thus requiring a large number of samples for a dynamic analysis of the degradation process [33,34].

4.1.6.X-ray microtomography (μCT)

Microfocus X-ray computed tomography (μCT) is a nondestructive 3D imaging method that can be used for analyzing the degradation of Mg alloy implants bothin situand in a static manner [98,193,194].In a similar manner as for mass loss measurements,the degradation rate is calculatedviathe observed volume lossΔV obtained from the images.As well as limitations associated with the used instrument,this method also has limitations that are related to the algorithm used to process the images and the values considered for the image parameters.

In addition to studying the degradation rate of Mg alloys,understanding the formation of precipitates on the implant surface is required to accurately model the protective nature of the degradation layer.To analyze the precipitates,a number of methods can be used,most prominently,scanning electron microscopy and energy-dispersive spectroscopy,X-ray diffraction and Fourier-transform infrared spectroscopy.

4.2.Calibration,validation,and verificatio of in silico studies

To test the reliability of the model three main stages are well established within the computational fields these stages are the calibration,validation,and verificatio [195].In studying thein vitrodegradation of Mg-based implants,model calibration plays a major role in determining the values of key parameters of the model based on the available experimental data of the same system or a similar system [124,132,192].For example;Bajger et al.[139] reported that the values of the diffusion coefficient differ with one order of magnitude in literature.Also,the estimation of the key parameters of the system was done by trial and error fittin and due to that these parameters were limited for certain systems or study conditions [123,139,156,157].The validation stage ofin vitrodegradation of the Mg-based alloys model involves validating the concepts of the electrochemical reactions,surface reactions,diffusion,forming and precipitation processes with an actualin vitroexperiment.At this stage,the degradationrate values,the percentage of mass loss and hydrogen release are validated against experiments.The third stage of checking the reliability of a model is the verification where the computational model and its implementation are correct[145,196,197].In the degradation models of Mg-based implants the verificatio of the mesh is one of the important steps to accurately predict the implant shape and the movement of the degradation surface as presented by Wu et al.[198] and Deshpande [132].

Regardless of the ability of the current computational systems (hardware and algorithms) to simulate complex processes,the reliability of these models is sometimes questionable.Experimental data,model concepts,limitations of simulators and even the implementation of these models are sources of uncertainty and uncertainty propagation within the system.It is necessary to control and quantify the uncertainties associated with these sources and different parameters affecting the system.Calibration,validation and verificatio only target certain aspects of the system uncertainty but the total uncertainty in the system is still unquantifie nor estimated [195] and a new approach is therefore needed to overcome this challenge.

Uncertainty Quantificatio (UQ) deals with the known unknowns of models.This fiel has grown in the last few decades due to the necessity to eliminate and quantify the uncertainties associated with different mathematical approaches.UQ quantitatively characterizes the proximity between both predictions and observations [199–201],through connecting the physical systems with the computational models simulating them,through tools and methodologies produced by combining different concepts from statistics,computational science,engineering and applied mathematics [195,202–204].

Recently,UQ has been integrated as an essential part of most computational studies due to the fact it makes the best use of the computational model by eliminating the uncertainties associated with them,pointing to the error sources and possible enhancements [200,205].The available models simulating the degradation process of Mg-based implants are subject to various types of uncertainties.The epistemic uncertainty,appears due to the model assumption,the understanding of the system and the different observation and measurements [195,203,204].The other type of uncertainty is the aleatory uncertainty,which is the non-reducible uncertainty of the system.These uncertainties are due to the natural variability in the model parameters,which can be quantifie by definin different distribution within the probabilistic framework [200,202,203].This building up of different uncertainties within each part of the degradation model results in the propagation of the uncertainty through the model and affects its predictions.The accumulated uncertainty within the system therefore plays an important role in the decisions made based on the model.The schematic diagram in Fig.14 summaries the uncertainty sources within the degradation system of Mgbased alloys.Consequently,quantifying the various uncertainties associated with the different aspects of the degradation process is highly important to produce a reliable mathematical framework that can accurately simulate the degradation process of Mg-based implants.

Fig.14.Schematic diagram of uncertainty sources within the degradation process of Mg-based implants,the red arrows represents the building of uncertainty within the system.(Inspired by [206]).

The degradation system of Mg-based implants is considered a large biochemical system,which is computationally expensive to evaluate.Furthermore,this system required the estimation of several missing key parameters.To estimate these parameters UQ provides several approaches and techniques[197,203,207].Kriging algorithms,also known as Gaussian process modeling,is one of the techniques applied to optimize and estimate the missing model parameters.Kriging estimates the optimal parameter of the degradation model without requiring extensive runs for the original expensive model and hence play a major role in reducing the computational cost and size of study data sets [208].

In a recent study by Zeller-Plumhoff and Albaraghtheh et al.[152],the key parameters of the degradation model of pure Mg in SBF were calibrated using a Kriging metamodel.These parameters were mainly reaction rate constants for the degradation and precipitation reactions.Using Kriging during the parameter estimation phase reduced the computational load from 5–23 min to 6–12 s and enhanced the model’s reliability.Additionally,the Kriging metamodels-based sensitivity analysis identifie a strong correlation between key parameters of the model,in particular precipitate formation on the surface of the implant.

Tak et al.[209] implemented Kriging algorithm to predict the corrosion rates of the metallic crude unit in a refiner process.The main challenge in this process was the inability of the available corrosion models to simulate the corrosion under the severe conditions.The Kriging model was developed to optimize the key parameters (pH,fl w rates and concentration of Cl−,Fe2+,H2S and NH3) of the corrosion process.The Kriging model was compared to a multiple linear regression and an artificia neural network and provided the best results.The reduction of computational cost and the good agreement of Kriging models are also reported by Kleijnen[210],where a qualitative and quantitative study of Kriging models of several systems was presented.In addition to parameter calibration,sensitivity analysis which identifie the parameters which affect the model the most is crucial in computational modeling,as it enhances the design of experiments of the studied system and serves to explain the behavior of this system.Sensitivity analysis provides a measure of confidenc in the quantifie model variables.Also,it identifie which parameters are contributing to the model behavior.This will help in generating accurate hypotheses about the system behavior [207,211,212].The sensitivity analysis may present a solution to the dimensionality problem of the degradation system of the Mg-based implant.A recent study by Wang et al.[205] presented a multiphysics modeling of tribocorrosion in aluminium alloys under uncertainty quantifi cation.Kriging was implemented to approximate and analyze the parameters and confidenc intervals of the model.Each output of the FE model could be augmented by the confi dence intervals corresponding to the UQ analysis.Furthermore,the Kriging model was tested against neural network(NN) model and the output of the Kriging model was in better agreement with the validation data than the NN model.The development of new methods for meta-modeling is ongoing,and in the future,more advanced meta-models,such as polynomial chaos Kriging and physics-informed neural networks should be evaluated for the use in implant degradation modeling.

Despite its obvious power and importance,UQ has not been fully recognisedin silicostudies of the degradation of biodegradable implants and remains far less understood in comparison with calibration,validation,and verificatio techniques.However,the UQ fiel is one of the richest and largest areas of computational research [213,214].UQ methods and techniques are able to overcome the main challenges in material science such as the multiscale simulations,time scales and the lack of key parameters.Furthermore,UQ methods and techniques are able to handle the propagation of different types and sources of uncertainties and errors within the material science field Therefore,we believe that UQ will in the future be used increasingly to support computational modeling of Mg degradation.

5.Summary and conclusions

In vitrostudies of the degradation of Mg-based implants are highly important in understanding the underlying mechanisms,revealing the connections of different parameters affecting the degradation and presenting a picture of the implant behavior under different physiological conditions.In this review,we presented the different interactions between the key factors affecting the degradation process of Mg-based implantsin vitro.Thein silicoapproach will help in reducing the time and the cost of several experimental studies by presenting a theoretical understanding of the process and the interactions taking place within it.A large number of existing studies in the broader literature have examined several computational approaches to model different aspects of the degradation process of Mg based alloys.

The literature review shows that the phenomenological approach provided the external visualization of the degradation process of the Mg-based implants,like the pits,cracks,and uniform degradation but these models were unable to capture the different interactions of Mg2+ions,precipitates,and dissolution within the system,which can be predicted by the physical models.Physical models,however,were able to capture the complex movement of the degradation surface.PF,PD and CA provided additional possibilities to study more aspects of the degradation process without requiring complex PDE implementation and solution.

Despite the important role of these models in enhancing the understanding and studying of the implant systems,the majority of these models are still limited to certain systems or under certain conditions.Up to date,modeling of different degradation mechanisms accounting for all the electrochemical and mechanical phenomena represents a hard challenge.The developed models need to be calibrated and verifie experimentally and theoretically.In the future,we recommend the integration of the uncertainty quantificatio (UQ) approach in studying the degradation process.This recommendation is driven by the various methods,techniques and algorithms provided by UQ,which not only enhance the model but also help,in a less complex form,in exploring the key factors affecting the system and its behavior.The application of UQ will increasing the reliability ofin silicoapproach and may help in fillin the gap between the different studies of the degradation process of Mg-based implants and accelerate the development process.

Declaration of Competing Interest

The authors declare that they have no known competing financia interests or personal relationships that could have appeared to influenc the work reported in this paper.

CRediT authorship contribution statement

Tamadur Albaraghtheh: Conceptualization,Writing –original draft.Regine Willumeit-Römer: Writing – review&editing.Berit Zeller-Plumhoff:Conceptualization,Writing – original draft.

Acknowledgments

The authors would like to thank Dr.Stefan Bruns for the fruitful discussions.The authors acknowledge funding from the Helmholtz-Incubator project Uncertainty Quantification