一种用于控制工业机器人运动轨迹误差的观测控制策略研究

马骉,郭鹏远,杨小强

(1.重庆城市职业学院工业机器人运维重庆市高校工程中心，重庆 402160；2.重庆文理学院智能制造工程学院，重庆 402160；3.重庆科创职业学院智能制造学院，重庆 402160)

0 前言

工业机器人的出现为人们的生产劳动提供了极大的帮助。工业机器人具有适用性广、可控性能好以及抗干扰能力强等特点，已被用于机械加工、航空航天以及医疗诊断等多种技术领域[1-4]。工业机器人运动轨迹的准确性与生产过程的安全性以及生产效率有着密切的关系，工业机器人运动轨迹的准确度越高，就越有助于提高生产过程的安全性与生产效率。

近年来，专家学者们研究出了较多的机器人运动轨迹控制方法，例如：YIN、PAN[5]基于机器人末端执行器的空间动力学特性，建立了鲁棒自适应控制律，在存在未知外部干扰和参数不确定性的情况下，通过结合鲁棒项和自适应项设计控制律，以足够的鲁棒性和精度跟踪末端执行器的期望轨迹，基于Lyapunov函数和Barbalat引理，最终保证了该控制的轨迹跟踪性能。GARRIZ、DOMINGO[6]提出了一种利用卡尔曼滤波器来实现机器人运动轨迹的控制方法，该方法定义了机器人手臂的运动学模型，然后将其集成到基于卡尔曼滤波器的算法中，以实现对工业机器人的轨迹控制。文献[7]提出了一种集成的直接/间接自适应鲁棒控制(DIARC)算法，该算法包括基于广义动量的间接自适应律，用于快速直接项补偿自适应瞬态，以及用于衰减不确定非线性的鲁棒反馈，简化了激励轨迹优化，并使用较少的参数捕捉主要动力学，进而控制机器人的运动轨迹。虽然这些方法都可以实现对机器人运动轨迹的控制，但是控制准确度还有待提高。

对此，本文作者对工业机器人的组成结构进行分析，并在机器人的坐标系下，利用机器人连杆间坐标系的变换矩阵，求取了机器人末端执行器的运动学模型；采用机器人的测量运动误差，构造了运动误差观测器，用于获取机器人的估计运动误差；接着通过神经网络控制器获取控制量，以实现对机器人运动轨迹的准确控制。实验中利用此方法对平面和空间标定轨迹进行了追踪测试，以验证此方法对工业机器人运动轨迹控制的优良性。

1 工业机器人的组成

工业机器人大致由底座、运动关节以及连接臂三部分组成。图1为工业机器人的机械结构模型图[8-10]。

图1 工业机器人的机械结构模型

图1所示工业机器人为六自由度工业机器人，由6个旋转关节组成，机器人末端执行器的运动就靠控制这6个旋转关节的动作来完成。从图1可见，在机器人的运动关节之间，都有一个连接臂，这种机械结构即为连杆结构。工业机器人的连接臂可被视为刚体杆件。

2 工业机器人的运动学模型

在分析工业机器人的运动学模型前，需要建立工业机器人的坐标系。工业机器人每一个关节处都需要建立一个坐标系。图2为工业机器人的坐标系[11-12]。

图2 工业机器人的坐标系

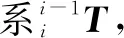
R(z,θi)T(0,0,di)

(1)

式中：R(xi-1,ai-1)、T(li-1,0,0)和R(z,θi)、T(0,0,di)的表述如下：

(2)

(3)

(4)

(5)

通过式(1)—式(5)，可得出机器人连杆间坐标系的变换矩阵T[14]为

T=

(6)

(7)

式中：n=[nx,ny,nz]为末端执行器的法线向量；u=[ux,uy,uz]为末端执行器的方向向量；h=[hx,hy,hz]为末端执行器的运动向量；p=[px,py,pz]为末端执行器的位置向量，其描述了末端执行器相对于底座坐标系的位置关系。末端执行器上n、u、h、p的关系如图3所示。

图3 机器人末端执行器各向量关系

通过n、u、h可求出末端执行器相对于底座坐标系的旋转矩阵R：

(8)

旋转矩阵R描述了末端执行器相对于底座坐标系的方向关系。

3 运动误差观测控制策略的设计

工业机器人的柔顺性易使得其运动轨迹与标定轨迹出现偏移，因此需要对工业机器人进行运动轨迹的控制，以提高其工作效率。由于机器人的准静态运动学误差会使得传感器在获取机器人实际运动轨迹时产生误差，从而使得计算出的标定运动轨迹与实际运动轨迹出现偏差，导致控制准确度下降。本文作者利用机器人的测量运动误差，建立了运动误差观测器，用于获取机器人的估计运动误差，并将估计运动误差联合神经网络控制器，以实现对机器人运动轨迹的准确控制。

测量末端执行器实际轨迹的传感器架，与末端执行器标称位置(文中称为标称架)之间的相对转换，描述了物理机器人和机器人运动学结构之间的转换误差。此转换过程中的动态误差转换过程为

(9)

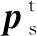
(10)

在一个n个连杆的机器人中，令其测量关节位置向量为q：

(11)

则依据式(7)，可得n个连杆组成的工业机器人的标称正向运动学模型为

(12)

机器人的传感器架与底座之间的变换模型为

(13)

机器人的标称架与底座之间的变换模型为

(14)

联合式(13)和式(14)可得：

(15)

合并式(9)(12)(13)(14)可得：

(16)

由此可得：

(17)

测量系统的一般形式可表述为

y=x+n

(18)

式中：x为状态向量；n为传感器噪声；y为测量运动误差：

y=em

吕英理事长代表理事会向大会做了题为“服务、发展、创新，提高煤炭加工利用水平”的工作报告；张绍强副理事长在会上做了关于“宣贯‘十二五’煤炭工业环境保护、资源综合利用及洗选加工规划”的报告；鞍山重型矿山机器股份有限公司董事长杨永柱代表会员单位在会上发言。大会还邀请煤炭科学研究总院北京煤化工研究分院副院长陈亚飞、中国石油规划总院副总工程师张福琴先后做了题为“我国低阶煤资源特征及其合理加工利用”及“C3/C4资源加工利用分析”的专题报告。

(19)

通过式(18)可得出观测器动力学函数为

(20)

(21)

联合式(19)—式(21)构造出运动误差观测器为

(22)

通过式(22)求取出运动误差后，再将其作为神经网络控制器的输入信号，求取控制信号，完成机器人运动轨迹的控制。

神经网络控制器为多输入单输出控制器，其结构示意如图4[5，15]所示。

图4 神经网络结构示意

在图4中，e=[e1,e2,…，en]和M=[M1,M2,…，Mn]以及W=[W1,W2,…，Wn]分别为输入矢量、基矢量和权重矢量。对于图4所示神经网络的输出值u为

(23)

4 实验结果

为了验证文中所提方法的有效性，在图5所示工业机器人本体的基础上，利用MATLAB软件建立实验环境，对所提运动误差观测控制策略(Motion Error Observation Control Strategy,MEOCS)进行实验。实验中将滑模控制策略(Sliding Mode Control Strategy,SMCS)作为对比。

图5 工业机器人本体

4.1 平面轨迹追踪实验

从图6可见：MEOCS和SMCS方法对平面标定运动轨迹进行追踪时都产生了一些追踪偏差，MEOCS的追踪运动轨迹比SMCS的更贴合标定运动轨迹，而且MEOCS的追踪运动轨迹比SMCS的波动更少，在偏离平面标定运动轨迹时，MEOCS方法比SMCS方法能更快地控制追踪运动轨迹重回标定运动轨迹。

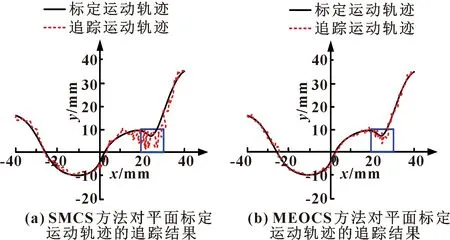
图6 MEOCS和SMCS方法对平面标定运动轨迹的追踪结果

为进一步观察MEOCS和SMCS方法对平面标定运动轨迹的追踪效果，取图6方框处两种方法对平面标定运动轨迹追踪结果，在y轴上产生的误差进行对比，如图7所示。

对比图7可知：MEOCS方法比SMCS方法在y轴上出现误差的次数更少，且MEOCS方法和SMCS方法追踪平面标定运动轨迹在y轴上产生的最大误差分别为4.8、7.3 mm。由此可见，MEOCS方法对机器人平面标定运动轨迹的追踪误差较小，追踪效果较好。

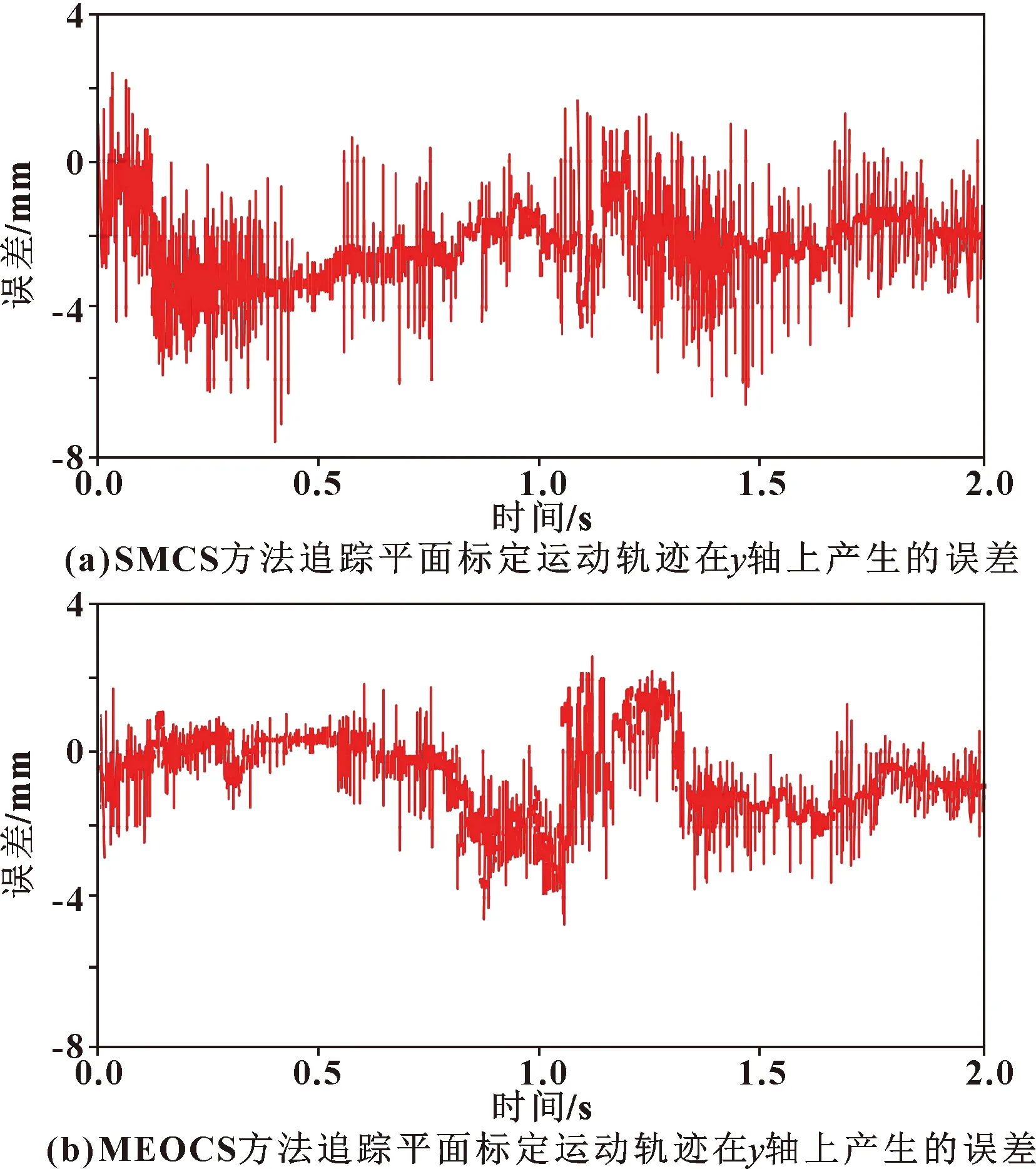
图7 MEOCS和SMCS方法追踪平面标定运动轨迹在y轴上产生的误差

4.2 空间轨迹追踪实验

在三维空间设定一个标定运动轨迹，采用MEOCS和SMCS方法对该空间标定运动轨迹进行追踪实验。MEOCS和SMCS方法对空间标定运动轨迹的追踪结果如图8所示。

通过观察图8可知：在追踪空间标定运动轨迹时，MEOCS方法比SMCS方法的追踪运动轨迹更趋于空间标定运动轨迹，出现偏离空间标定运动轨迹的次数更少，而且偏离的幅度也更小。由此可见，MEOCS方法对空间标定运动轨迹的追踪准确度较高，能对工业机器人运动轨迹进行精准的控制。

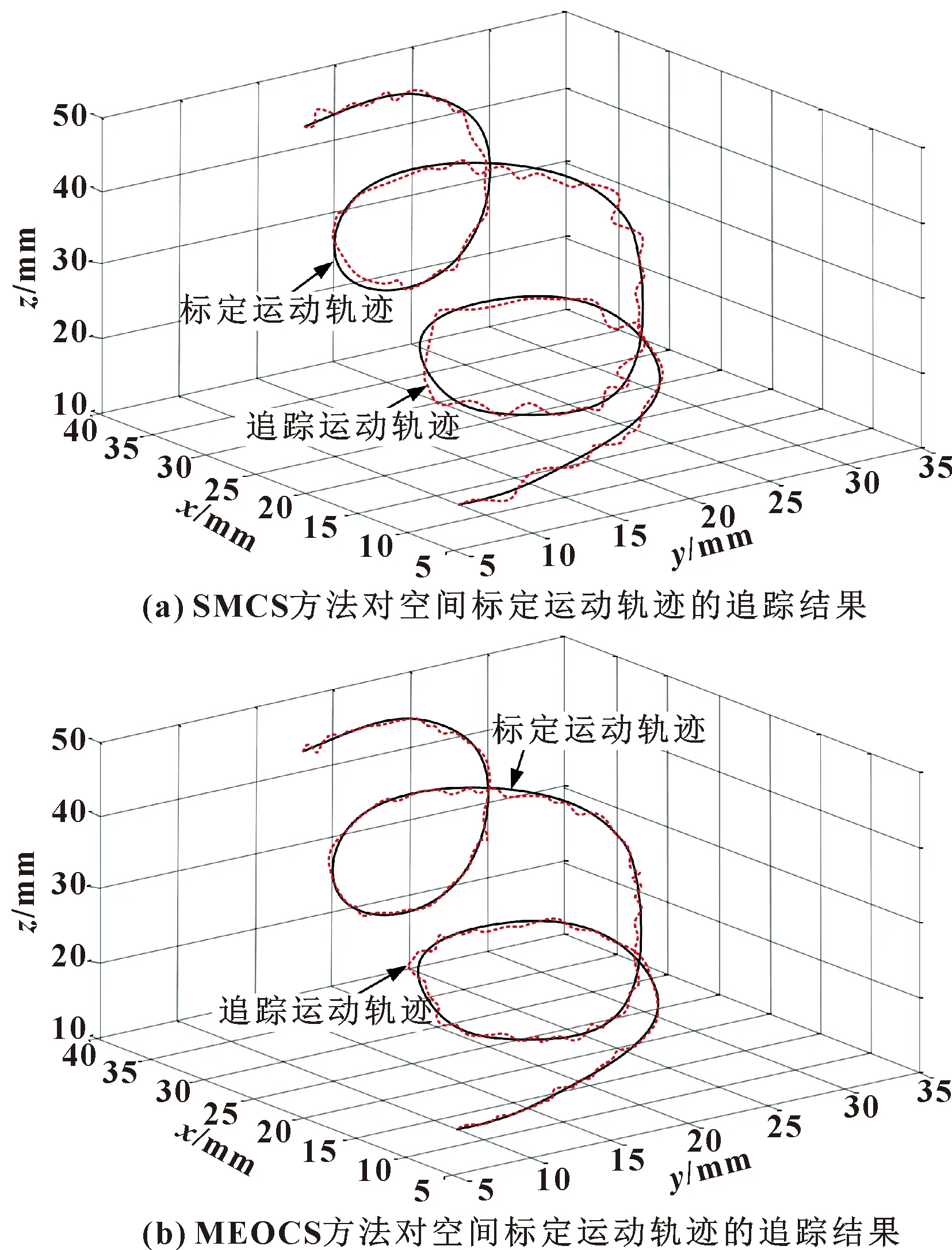
图8 MEOCS和SMCS方法对空间标定运动轨迹的追踪结果

5 结语

从工业机器人的机械结构出发，分析其组成结构。在工业机器人的坐标系上，通过求取机器人不同坐标系间的变换值，得到了机器人末端执行器的运动学模型。通过测量运动误差，建立了传感器架和标称架的动态误差转换矩阵；在机器人正向运动学模型的基础上，通过传感器架以及标称架与底座之间的变换模型，计算了传感器架相对于标称架之间的位置向量及动态误差变换的旋转矩阵，得到了测量运动误差值；进而利用测量运动误差值，构造了运动误差观测器，以获取机器人的运动误差。将机器人的运动误差作为输入量，通过神经网络控制器，计算出了控制量，从而实现对机器人运动轨迹的控制。实验结果表明：文中方法对机器人平面和空间标定运动轨迹的追踪效果都较为理想，能准确控制机器人按照标定运动轨迹工作。