融合动态窗与改进RRT的全位置机器人路径规划算法研究

张海波，严小珊，毕齐林，唐惠玲

(1.广州航海学院土木与工程管理学院，广东广州510725；2.广东工业大学物理与光电工程学院，广东广州 510006)

0 前言

传统的轮式、腿式、履带式等移动机器人难以在狭小空间移动，全位置式移动机器人(简称MW-WH-OIR)有助于改善这种情况，因此具有较广泛的应用前景及重要的研究意义。

在“十三五”、“工业4.0计划”等政策的推动下，我国巡检业加快了向规模化、自动化、智能化方向转型的步伐，工业移动机器人也迎来了快速发展的战略机遇期[1-2]。目前，国内的巡检业(如变电站巡检，轨道交通巡检，城市应急安防巡检业)还存在大量人工巡检、多固定点监控的方法。此类工作量大、枯燥，有时候还存在一定危险，很多时候靠人眼并不能及时发现缺陷，效率低、周期长，存在极大的盲区，易造成潜在的安全隐患。此外，多固定点监视范围有限、成本高、实用性差，不能满足现代需求。

MW-WH-OIR能够在任意方向移动，灵活性好，搭载摄像头便可以大大扩展检测范围，可以广泛应用于智能巡检领域。国内智能巡检市场对工业移动机器人的需求正在不断增加，然而在移动机器人的相关技术研究中，导航技术是最核心的技术，路径规划则是导航技术的一项重要内容。

工业移动机器人成为当代工业重要利器的同时，常常要考虑其运动规划问题，高效的路径规划有利于提高工作效率。如何在复杂的动态障碍物环境下，规划一条实时的从起始点到目标点无碰撞的可行路径是MW-WH-OIR技术研发的关键。

MW-WH-OIR的路径规划是指在具有障碍物的复杂环境下，按照规划路径的某个测度(如时间最短、路径最优、能量消耗最低等)，在任务区域内寻找一条从起始点到目标点与障碍物无碰撞的可行路径[3]。20世纪70年代至今，国内外学者对此进行了大量的研究，同时还提出了许多适用于不同应用场景下的路径规划算法并不断进行改进、优化。2007年赵晓等人[4]利用A*算法实现了移动机器人的无碰撞路径规划。王淼弛[5]针对A*算法存在的次优路径问题，改进了A*算法的启发搜索策略，优化了路径长度，同时提高了路径平滑度；王奇志[6]针对传统人工势场法出现的零势能域现象，采用限定范围的方法改进了人工势场法，实现了多障碍物情况下机器人快速、实时、避障的路径规划。2010年SHI等[7]为解决传统人工势场法用于移动机器人运动规划时，出现目标点距离障碍物太近而无法到达目标点以及存在局部极小点的陷阱问题，提出了缩小障碍物影响范围、障碍物影响范围分层的改进方法，使得算法适用于移动机器人在各种复杂环境下的路径规划。李宝霞[8]针对模糊系统的隶属度函数确定过程繁琐问题，将遗传算法结合到模糊系统中，对模糊算法进行改进，生成了模糊遗传算法。

以上常用的路径规划算法在简单的环境下能快速地找到最优路径，但其没有考虑非完整性约束问题，也不适合解决高维空间多自由度机器人复杂约束下的运动规划问题，可能导致实际路径不可行，不能满足移动机器人运动规划的实时性。

为此，基于随机采样的运动规划算法，YANG等提出了一种基于采样的快速随机扩展树方法(Rapidly-exploring Random Trees，RRT)算法[9]。由于RRT算法的快速搜索随机性，增量式搜索方式能够把非完整性约束或非完整性动力学约束考虑到运动规划中，因此非常适合解决高维空间多自由度机器人在复杂环境和变化场景中的运动规划问题。樊晓平和李双艳[10]针对复杂的动态环境，将RRT算法与滚动规划结合，同时在RRT算法中引入选择性参数BIAS，实现了向目标点快速收敛的实时在线路径规划。乔慧芬等[11]为实现动态不确定环境下实时路径规划，结合人工势场法下规划的初始路径和RRT算法指导下的局部路径，有效实现了移动机器人的无碰撞实时路径规划。

本文作者基于MW-WH-OIR的工作环境，提出一种改进的快速扩展随机树算法，使MW-WH-OIR能够在一个复杂的动态环境下进行在线实时路径规划。

实际情况下，MW-WH-OIR更多时候需要对动态环境变化实时做出动作，并不断寻找最优可行路径。ZHUANG等[12]基于极坐标空间，实现了以机器人期望运动方向角为指标的动态不确定环境下移动机器人的在线实时路径规划。曾碧和杨宜民[13]利用模糊描述对环境进行建模,将改进的蚁群算法与机器人滚动在线路径规化方法相结合，实现了动态环境下在线实时规划问题。以上算法都未考虑移动机构的非完整约束条件。快速搜索随机树可在环境中的从起始点开始快速随机扩展搜索树，直到寻找到目标点，其结构简单、搜索能力强且考虑了执行机构的非完整约束条件，还易于与其他算法结合生成一个新的可行算法。在国内，RRT算法应用于已知的环境下的研究已经很成熟，但应用于动态环境下的实时路径规划的研究还较少。

在实际工作中，MW-WH-OIR多处于一个复杂的动态环境，传统的RRT算法及大多数改进后的RRT算法生成的路径往往不能被采用。因此，如何使MW-WH-OIR在一个复杂的动态环境下进行高效的在线实时避障及路径规划是文中需要解决的问题。

1 传统RRT算法

1.1 传统RRT算法基本流程

传统RRT算法相较其他路径规划算法更加具备快速搜索的能力，能够很好地适应动态变化的环境，也因其快速扩展的随机性，使得该算法具有很强的避障功能。图1所示为传统RRT算法的流程。

图1 传统RRT算法基本流程

1.2 传统RRT算法的基本原理

传统RRT算法不断地将树枝从起始节点Xinit(根节点)随机扩展到目标节点Xgoal，其过程中合理避开障碍物，遍历生成随机树T，最后选取一条最优的可行路径[16]。传统的RRT算法：

Algorithm1：传统RRT

1：TU←Xinit；

2：while(n←1 to Nmax)do

3：Xrand← Sample_node(Xfree)；

4：Xnear←Nearclose(Xrand，TU)；

6：Xnew←Steer(Xnear，Xrand)；

7：if Check_path(Xnearest，Xnew)= = true then；

8：Add_node(Xnew)；

9：end if

10：end while

11：return TU；

传统RRT算法的基本步骤如下：

步骤1：初始化随机树T后将给定起始点Xinit添加到随机树T作为根节点；

步骤2：在Wfree空间中随机获取一个生长树节点Xrand；

步骤3：用Nearclose()函数计算树T中与Xrand距离最近的扩展节点Xnear；

步骤4：用Steer()函数在Xrand与Xnear方向上生长新节点Xnew；

步骤5：判断Xnew生长区域是否存在障碍物，若是，则跳转进行步骤3；若否，则在随机树T上添加一个新节点Xnewi(i∈N，N为自然数)

步骤6：判断是否满足Xrandi=Xgoal或者Xnewi∈Xgoal的条件，若不满足条件，则跳转进行步骤4；若满足条件，则从目标节点Xgoal开始依次找到父亲节点直到起始点Xinit为止，之后返回一条可行的规划路径，结束程序。

2 基于改进RRT算法的MW-WH-OIR实时路径规划方法理论分析

2.1 定义滚动窗口

MW-WH-OIR在进行管道、轨道、安防巡检作业时，常处于一个复杂动态障碍物环境下，为此首要考虑路径规划的实时性。全局路径规划方法运算时间太长，不适合动态复杂环境下的路径规划，为此文中采用局部路径规划方法。为满足路径规划的实时性，将传感器检测范围视为一个可进行自适应调节大小的窗口(文中视检测范围是一个半圆)，如图2所示，当H2大于检测范围时，对整个路径进行多阶段的规划。

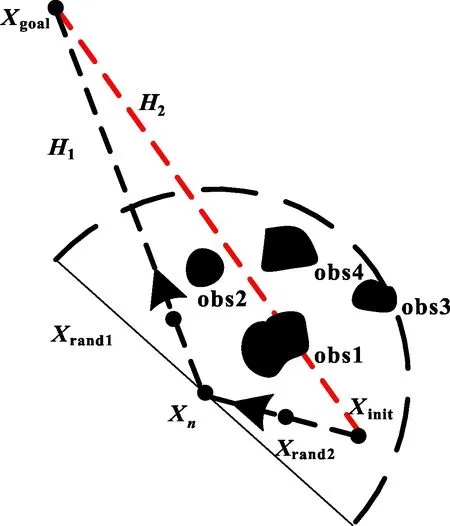
图2 滚动窗口示意

2.2 无障碍物时的MW-WH-OIR实时路径规划

通过GPS导航系统确定起始点Xinit与目标点Xgoal位置，若起始节点与目标节点之间，不存在障碍物时，起始节点Xinit与目标节点Xgoal之间的连线距离就是MW-WH-OIR所要行走的最短可行路径，如图3所示。

图3 无障碍物处理模型

2.3 有障碍物时的MW-WH-OIR实时路径规划

动态障碍物的位置会随着时间发生变化，故建模是以时间为轴建立方程。障碍物任意时刻的位置状态用(x，y，t)表示。

2.3.1 面向MW-WH-OIR的匀速障碍物预测模型

如图4所示，假设障碍物以速度v(t)=b匀速移动，在t时刻于点A位置处(xi，yi，t)被滑动窗口检测到，而下一时刻t+Δt时，处于点B(Δt取值极小)，当Δt取极小值时，AB之间的连线可视为一条直线，直线AB与X轴之间的夹角为θ，则对于障碍物从t→t+Δt过程中，它的位置坐标变化情况如下：

图4 匀速障碍物预测模型

(1)

通过公式(1)可以快速计算出任意时刻障碍物的移动位置。

2.3.2 面向MW-WH-OIR的变速障碍物预测模型

MW-WH-OIR在二维平面工作，由于传感器可以实时获取局部动态障碍物的位置信息，文中通过传感器在前期获取的动态障碍物位置信息，结合自回归模型预测下一时刻动态障碍物的运动位置，进行局部规划，避开障碍物。

如图5所示，假设传感器的滑动窗口检测到的动态障碍物为obsq(q∈N)，并记录了该障碍物上一时刻和当前时刻的位置信息，记为sq(t-1)、sq(t)(t∈N)，由此建立预测下一时刻位置sq(t+1)的自回归模型：

图5 存在变速的障碍物预测模型

sq(t)=λ1sq(t-1)+e(t)

(2)

相应的推导n阶自回归模型：

(3)

其中：e(t)为位置预测误差；λ为位置的回归系数。

同理对动态障碍物的加速度aq进行n阶自回归建模：

(4)

其中：p(t)为加速度预测误差；β为加速度的回归系数。

速度与位置的关系式：

vq(t)=sq(t)-sq(t-1)

(5)

加速度与速度关系式：

aq(t)=vq(t)-vq(t-1)

(6)

结合上式，易得加速度与位置的关系式：

aq(t)=sq(t)-2sq(t-1)+sq(t-2)

(7)

加速度回归系数β通过最小二乘法拟合，由公式(4)可引入加速度的残差平方和函数：

(8)

(9)

通过对E(β)进行微分求最值，可以得到：

(10)

当加速度的回归系数βq与时间相关时，在残差平方和函数取值最小的函数中引入一个指数权重因子μ(0<μ<1),μ越趋近于1，表明加速度变化得越快。

(11)

求上式的解：

(12)

当能拟合估算回归系数βq，便可以计算下一时刻动态障碍物的预测位置，即：

(13)

3 面向MW-WH-OIR的改进RRT算法

3.1 MW-WH-OIR运动学模型

Mecanum Wheel能实现全方位移动，1973年由瑞士人LION发明[14]。它有3个自由度，即绕辊子轴转动、绕轮子轴转动、绕辊子与地面的接触点转动。MW-WH-OIR的移动机构主要采用4个Mecanum Wheel，可以实现任意方向的自由移动，其转弯半径近似为零，非常适合代替作业人员在工作空间狭小或对机器人的机动性要求较高的场合，如大型管道内侧巡检、变电站巡检、城市应急安防巡检等，因而在工业上应用越来越广泛[15]。本文作者针对MW-WH-OIR的路径规划分析时，可以不考虑其转弯半径限制的问题。以下对MW-WH-OIR运动学模型进行分析。

如图6所示，以O为原点建立坐标系，Y轴为MW-WH-OIR的正前方，X轴为MW-WH-OIR正右方。vn(n=1，2，3，4)为4个Mecanum Wheel上对应与地面接触的转动辊子绕轴的自身线速度；r为Mecanum Wheel的半径，则：vn=r×ωn(n=1，2，3，4)；ωn(n=1，2，3，4)为对应4个Mecanum Wheel的自身角速度；vx、vy分别为MW-WH-OIR在X、Y方向的移动速度；ω为绕中心点O垂直轴转动的角速度；α为Mecanum Wheel轮毂轴线和辊子轴线的夹角；2L2、2L1为机器人车身的长和宽。

图6 MW-WH-OIR运动学分析示意

若vx、vy已知，求4个轮子的线速度vn，则根据MW-WH-OIR运动学分析得计算公式如下：

v1=vy-vxtanα-(L2tanα+L1)ω

(14)

v2=vy+vxtanα+(L2tanα+L1)ω

(15)

v3=vy+vxtanα-(L2tanα+L1)ω

(16)

v4=vy-vxtanα+(L2tanα+L1)ω

(17)

反之，若4个轮子的线速度vn已知，即可求解MW-WH-OIR在X、Y方向上的移动速度(vx，vy)及相应的角速度ω，公式如下：

(18)

vy=0.25(v1+v2+v3+v4)

(19)

(20)

结合公式(14)—(17)，可分析MW-WH-OIR在各个方向上的移动情况，4种典型MW-WH-OIR的移动情况和4个Mecanum Wheel转向关系如图7所示。

图7 4种典型MW-WH-OIR移动情况

3.2 改进RRT算法

改进的RRT算法针对上述讨论的传统RRT算法存在的不足之处进行改进和创新，同时将其应用于更加复杂的动态环境下，扩展了算法的应用范围，其中考虑了MW-WH-OIR车身约束，从而更加符合MW-WH-OIR的实际工作情况。以下为改进RRT算法的伪代码：

Algorithm2：改进RRT

1：构建：仿真环境地图；

2：定义环境信息：机器人运动状态点Xinit、目标点Xgoal、子目标点Zgoal、步长Stepsize、安全阈值范围Q；

3：检测：判断起始点、目标点是否在仿真地图的障碍物上，若是，则退出，否则继续；

4：TU←Xinit；

5：while N>Nmaxdo；

6：Update(Zgoal)

7：obsn←Sample_obs;(n=1,2)；

8： Filter(Xnearest，Xnew)

9：Index_node = Index_tree(Xrand)；

10：while Index_node> 1 do

11：Update_node(Xrand)；

12：Select(Xnew，Xnear)

13：end while；

14：end while；

15：return T；

Function：Update(Zgoal，Xgoal)

1：while Xgoal==Zgoaldo

2：if Checkpath1(Zgoal)

3：Zgoal← Get(Zgoal)；

4：else if (a1Q))

5：Zgoal← Get(A1)；

6：else

7：Zgoal←Get(A2)

8：end if

9：if Xgoal⊆S

10：Xgoal=Zgoal

11：end if

12：end while

Function：Filter(Xnearest，Xnew)

1：Xrand← Sample_node；

2：Xnearest← Nearclose(Xrand，TU)；

3：Index_node = Index_tree(Xrand)；

4：for Xnearest∈Xneardo

5：if Xnear≠ Ø；

6： Total C = Cost(Xnearest)+Cost(Xnew，)；

7：end if；

8：if Total C1==min(total C)；

9：Xrand←Xnearest；

10：end if；

11：end for；

Function：Select(Xnew，Xnear)

1：if Checkpath2(Xnear，Xnew)&distance(Xnew>Q)；

2：Xnew← New_node(Xnewest，Xrand)；

3：else;

4：delete(Xnew)；

5：end if;

为弥补传统RRT算法的不足，本文作者提出的Algorithm2在Algorithm1的基础上添加了3个函数，下面对Algorithm2中的3个重要函数进行简单的介绍。

3.2.1 建立最小安全距离Q模型

由于传统RRT算法中并没有考虑移动机器人车身尺寸D的约束，故在规划路径过程中存在生长节点靠近障碍物的现象。当生长节点已经与障碍物粘在一起，MW-WH-OIR沿着该路径行走时必定会跟障碍物发生碰撞，损坏车身。为避免MW-WH-OIR与障碍物发生碰撞，设置最小安全距离Q(Algorithm2：第22～26行，其中Q>D)，如图8所示，障碍物边缘扩展的黄色区域即是安全阈值范围Q，令生长节点禁止扩展到安全阈值范围内，这样便使得MW-WH-OIR在移动过程中与障碍物始终保持一定的安全距离。以下为安全阈值Q算法：

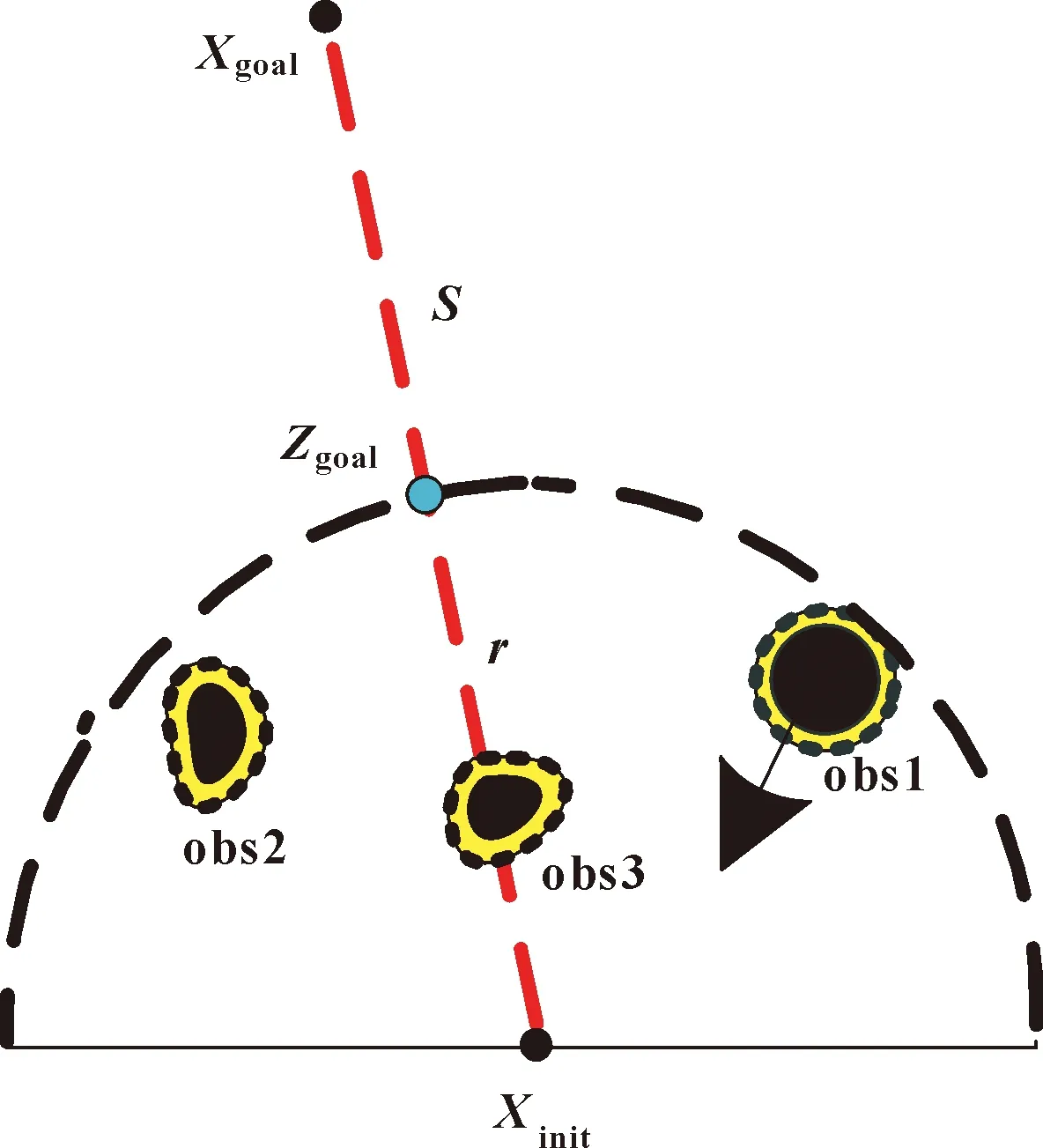
图8 设置安全阈值

Algorithm3：Select(Xnew，Xnear)

1：if Checkpath(Xnear，Xnew)&distance(Xnew>Q)；

2：Xnew← New_node(Xnewest，Xrand)；

3：else;

4：delete(Xnew)；

5：end if;

在检测生长节点Xnew是否与障碍物碰撞的同时判断与障碍物的距离是否大于Q值，若是，则添加新的生长节点，否则删除Xnew，重新寻找符合条件的Xnew。

3.2.2 子目标点的选取及更新算法

图9 子目标节点的选取及更新

Algorithm4：Update(Zgoal，Xgoal)

1：while Xgoal==Zgoaldo

2：if Checkpath1(Zgoal)

3：Zgoal← Get(Zgoal)；

4：elseif (a1Q))

5：Zgoal← Get(A1)；

6：else

7：Zgoal←Get(A2)

8：end if

9：if Xgoal⊆S

10：Xgoal=Zgoal

11：end if

11：end while

3.2.3 过滤无用节点

在基本RRT树枝生长过程中，会生成许多不必要的树枝，需要大量的迭代次数才能找到目标点，而且生成的路径曲折冗长、不平滑，耗费大量的搜索时间，搜索效率极低[17]。

为解决以上问题，本文作者在传统RRT算法的基础上添加了一个过滤不必要节点的过程(Algorithm5：第5～9行)，仅保留一个最优生长结点，如图10所示。品红色的生长节点明显偏离Zgoal，不是最优生长节点故将它过滤。这样就降低了迭代次数，大大提高搜索效率，减少冗余节点，路径的平滑度也有所提升。

图10 过滤无用节点

Algorithm5：Filter(Xnearest，Xnew)：

1：Xrand← Sample_node；

2：Xnearest← Nearclose(Xrand，TU)；

3：Index_node = Index_tree(Xrand)；

4：for Xnearest∈Xneardo

5：if Xnear≠ Ø；

6： Total C = Cost(Xnearest)+Cost(Xnew，)；

7：end if；

8：if Total C1==min(total C)；

9：Xrand←Xnearest；

10：end if；

11：end for；

当Xnear不为空集时，寻找Xnear集合中与Xnew形成最小长度代价的Xnearest，最后赋值给Xrand进行路径规划。

4 仿真实验

通过建立上述模型和RRT实时路径规划算法，在MATLAB2018a下进行了仿真实验。实验用计算机配置如下：处理器为Intel-Core-i5-7200，Xeon(R)，主频为3.10 GHz，内存为16 GB，操作系统为64位Windows10。实验设置地图大小为500×500(无量纲)，如图11所示。此次仿真实验中设置传统RRT算法在静态障碍物环境下的生长步长为25，随机生长节点概率阈值为20；起始点Xinit=(5,499)，子目标点Zgoal=(150,300)，目标点Xgoal=(499,5)。

图11 传统RRT算法路径规划仿真实验

利用改进的RRT算法将MW-WH-OIR的工作环境建模定位于500×500的地图区域，如图12中左上角为机器人第一次局部检测范围内路径规划的全过程，圆形的障碍物为可视范围内的随机动态障碍物，其余为静态障碍物，其中动态障碍物的起始点是任意设定的。

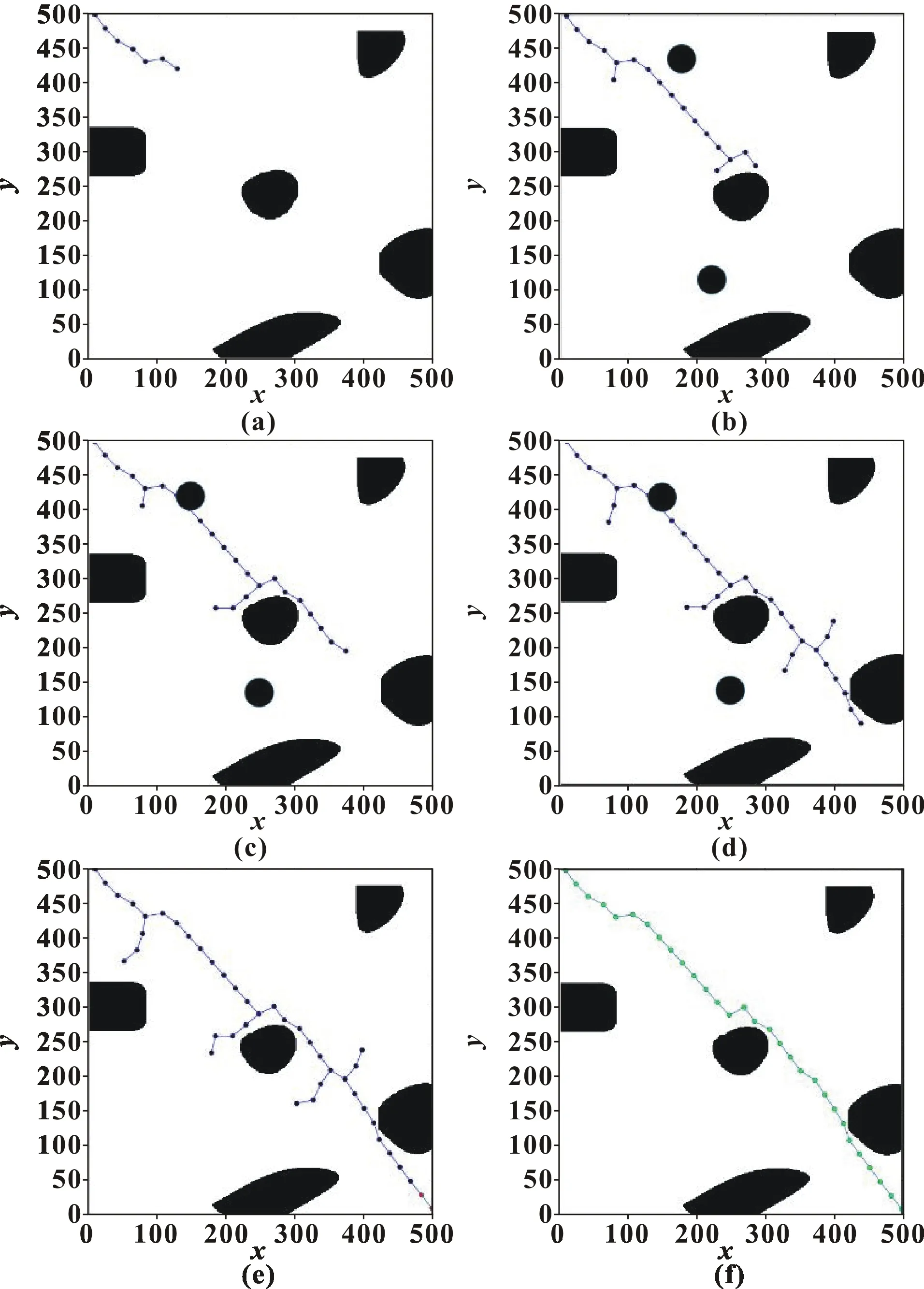
图12 基于改进RRT算法的实时路径规划仿真实验

4.1 传统RRT算法MW-WH-OIR路径规划仿真

传统RRT算法在500×500的复杂环境下(环境中的障碍物都为静态)的规划路径如图11所示，节点表示MW-WH-OIR经过的路径。由图11可以明显看出：随机树的生长区域几乎覆盖了整个工作环境，整个过程需要经过大量的迭代才能找到目标点Xgoal，极大地降低了搜索效率。图11(d)中的最终规划路径存在大量的冗余点，路径较为曲折，甚至在一些空旷区域内也存在许多弯曲的路径，偏离最优解。此外，还存在生长节点贴近障碍物的现象，如图11(d)红色标注)，在实际驾驶过程很容易与障碍物发生碰撞。

4.2 改进RRT算法MW-WH-OIR实时路径规划仿真

对比图11、图12的仿真结果可知:相较于传统RRT算法，改进的RRT算法规划路径并没有出现大量的冗余点、曲折点，树枝生长过程中能够顺利地避开障碍物，始终与障碍物保持一定的安全距离，最终朝向子目标点生长。此外，由图12可知，本文作者提出的算法解决了路径曲折、树枝生长无方向性、搜索效率低的问题，进而大幅度提高了规划路径平滑度，同时避免了MW-WH-OIR与障碍物发生碰撞的现象，满足移动机器人的实际移动需求。

4.3 实验结果对比分析

为了更好地验证算法性能，分别对3种算法在文中设定的障碍物环境下进行500次仿真实验，得到每种算法规划所需的最小、最大以及平均时间的实验数据，如表1所示。

表1 复杂障碍物环境下算法路径规划性能数据

从表1可看出：不管是在简单静态障碍物威胁还是复杂动态障碍物威胁环境下，文中算法的规划时间均是最少的，与传统RRT算法相比较，它将搜索效率提高了43%。

5 结论

针对传统RRT算法应用于MW-WH-OIR生成的路径存在路径曲折、搜索效率低、树枝生长缺乏目标引导性甚至路径不可行的问题，首先，添加了删除无用节点策略，减少冗余点，提高探索效率；其次，提出了子目标点的选取原则，在能够保证顺利避障的前提下，使得生长树优先朝向目标点生长；最后，设置合适的安全阈值范围，使移动机器人与障碍物能够保持一定的安全距离。最终提高了树枝生长效率，生成的路径较为平滑，能够更好地应用于MW-WH-OIR的实际工作中。