从直接度量走向间接度量
——《长方形和正方形的面积》教学设计
2022-12-28成艳斌
文 成艳斌 刘 敬
【教学内容】
苏教版三年级下册第66~68页。
【教学过程】
一、项目实践,发现关系
1.回顾旧知,唤醒经验。
师:下面两幅图的面积各是多少?说明理由。
生:图1 包含8 个1cm2,它的面积是8cm2;图2 是长方形,每行摆了5 个1dm2,能摆3 行,面积是15dm2。
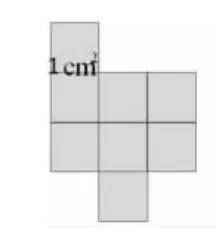
图1
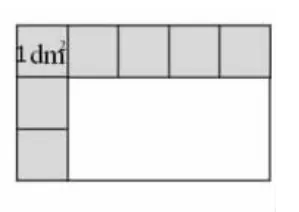
图2
师:测量图形的面积时,可以用面积单位满铺,也可以铺一部分,总之,一个图形的面积有多大,要看它包含有多少个面积单位。
2.提出问题,激发需求。
生活中比篮球场地更大的长方形还有很多,有什么简便方法能得到它们的面积呢?
3.目标引领,成果分享。
师:大家课前进行了分组实践,也带来了丰硕的成果,和大家分享一下吧。
生1:我们组是用1 个1m2的正方形摆的。先沿着篮球场的长边摆,摆一次,做个记号,再摆一次,再做个记号……最后发现长边能摆28 个;用同样的方法沿篮球场的宽边摆,一共能摆15 个。因为每行摆28 个,能摆15 行,所以28×15=420(个),篮球场的面积包含420 个1m2,就是420m2。
生2:我们组和他们一样,一开始也是这么摆的,但我们觉得比较麻烦,反正要做标记,索性就找体育老师借来了卷尺,先测出篮球场的长是28m,也就是28 个1m,每个1m 可以放一个1m2的正方形,说明能摆28 个1m2。再测量篮球场的宽是15m,就是15 个1m,说明能摆15 行。一共28×15=420(个),篮球场的面积也是420m2。
4.优化方法,引发猜想。
师:观察这两种方法,有什么相同,有什么不同?
生:计算方法相同,都找到了每行摆28 个,能摆15 行,都用每行的个数乘行数计算了面积单位的总个数。不同在操作过程,一个是摆的,一个是量的。
师:如果再测量一个更大的长方形面积,你选择哪种方法?为什么?
生:我选“量”。因为测量出长,就能推想出一行的单位个数;测量出宽,就能推想出行数。面积单位的总个数不一定非得靠“摆”,也可以“推想”。
师:通过测量长方形的长和宽,间接推想长方形包含有多少个面积单位,这种方法固然简单,但在测量别的长方形面积时是不是也适用,我们还要继续探究。
二、小心求证,总结规律
1.自主探索,间接度量。
(1)独立思考。
教师出示《学习单》,提出操作要求:
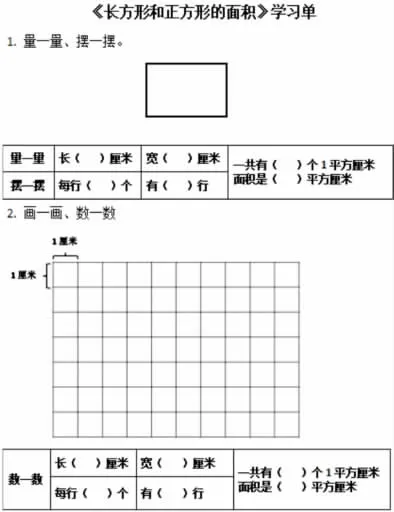
第一,量一量、摆一摆。先测量给定长方形的长和宽,再摆一摆、填一填。
第二,画一画、数一数。在方格纸上任意画一个长方形,再次求证。
(学生独立操作,自主思考,完成《学习单》)
(2)交流分享。
生1:我先测量了长方形的长是3cm,宽是2cm,然后用1cm2的单位去铺,每行摆了3 个,摆了2行。我发现长方形的长与每行摆的个数相等,宽与行数相等。一共有6 个1cm2,总面积是6cm2。
生2:不需要全摆满,只摆一行一列,也能知道每行摆3 个,摆2 行。
生3:我画了一个长6cm、宽4cm 的长方形,数了数格子,每行有6 个1cm2,有4 行,面积是24cm2。
生4:我也是用长乘宽计算的,我画的长方形长8cm、宽4cm,每行8 个,有4 行,面积是32cm2,也符合规律。
师:看来大家已经开始发现规律了。
(3)解决冲突。
生:我画的就不符合规律(如图)。长方形的长是4cm,每行有3个单位;宽是3cm,却有4 行。
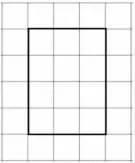
(教师组织学生讨论,解决问题)
生:不矛盾,把你画的长方形横过来,就对应了。
生:也可以这么想,宽是3cm,对应每行有3 个单位;长是4cm,对应有4 行,总数量也没变,也符合规律。
师:通过测量长方形的长和宽,间接推想长方形包含有多少个面积单位,这种方法是不是具有普遍性,你心里有答案了吗?
生:这种方法适用于所有的长方形。即使是刚才的特殊情况,这种规律也成立。
师:今天,我们在实际的面积测量中,主动沟通了长度单位和面积单位之间的联系,每量出一个1m,就对应了1 个1m2,看似测量了两个长度,实则是在推想面积单位的个数!这就是新旧知识之间的衔接,也是大家的活学活用。
2.抽象概括,得出结论。
师:既然我们已经发现了普遍规律,那你们能试着说说长方形的面积怎样计算吗?
(学生小组讨论,有理有据地推理)
生:长方形的面积就是看长方形包含多少个面积单位。测量出长,就能推想出每行摆几个面积单位;测量出宽,就能推想出摆这样的几行;用每行个数乘行数就能知道它的面积。长方形竖起来的情况也符合这个规律,所以,不管长方形怎么摆,长方形的面积都可以用长×宽来计算。
师:如果用S 表示长方形的面积,用a 和b 分别表示长方形的长和宽,公式怎么简写呢?
生:S=a×b。
3. 联系衔接,整体建构。
师:还记得上节课我们学面积单位,用1dm2测量数学书封面的面积时,并不能正好铺满,结果取了一个近似值。可是把这个问题放在今天这节课,你是否产生了新的疑问,用长乘宽计算长方形的面积,这种方法真的正确吗?
(学生先小组讨论,再集体反馈)
生:用1dm2不能铺满,就换1cm2来铺。我们沿着宽摆了18 个1cm2,沿着长摆了24 个1cm2,最后还是可以用长乘宽计算。
生:我用尺子测出数学书的封面长24cm、宽18cm,就可以推想出和刚才那个组一样的摆法,还是可以用24×18 来计算面积。
师:看来,大一些的面积单位不能铺满,不代表其他面积单位也不能铺满,换个小一点的面积单位就可以了,如果还不行,那就换个再小一点的面积单位……这样我们总能找到长对应的每行个数、宽对应的行数。
三、分层练习,巩固迁移
1.基础练习。
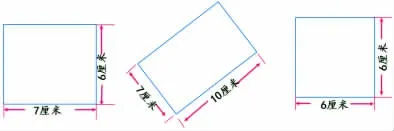
(学生先自己独立解决,再全班反馈。反馈时,重点放在正方形的面积计算)
师:第三个图形是一个正方形,怎么计算它的面积?
生:还是长乘宽,只不过它稍微特殊一些,长和宽都等于6。
生:边长×边长,一个边长可以推想出每行的个数,另一个边长推想出行数。
师:大家能利用长方形的面
积计算公式,推理出正方形的面积计算公式,真好!看起来一样的
两个乘数6,其实表示的意义是不一样的。如果用S 表示正方形的面积,用a 表示正方形的边长,公式又可以怎样简写呢?
生:S=a×a。
2.解决问题。
师:生活中有很多长方形的面积,并不是画好了图形等我们来算的。比如,你能从以下这个题组中找到长方形,并计算它的面积吗?
(1)一辆洒水车,洒水的宽度是8 米,每分钟行驶60 米。洒水车每分钟洒水的面积是多少?
(2)压路机前轮轮宽2 米,这种压路机前轮滚动一周大约可前进4 米。压路机前轮滚动一周压过路面的面积是多少?
(学生独立思考,小组交流,集体反馈。教师在适当的时机辅以动画演示,帮助学生理解“图形运动”背景下的长方形面积计算)
