基于稀疏贝叶斯学习的超材料孔径计算微波成像系统离网格成像方法

傅昊升 洪 灵 戴奉周*

①(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

②(陕西师范大学计算机学院 西安 710062)

1 引言

最近，基于超材料孔径(Metamaterial Aperture,MA)的计算微波成像(Computational Microwave Imaging, CMI)系统以其使用便携的硬件设备进行信息检索而受到广泛关注[1–8]。现有的微波成像体制主要包括合成孔径微波成像和实孔径微波成像。合成孔径微波成像利用目标场景与测量系统的相对运动形成一个电大尺寸虚孔径以获得高方位向分辨率，例如合成孔径雷达[9]。实孔径成像系统是利用多个收发通道构成的真实物理孔径获得方位向分辨率，例如MIMO (Multiple Input Multiple Output)[10]。不同于传统的实孔径微波成像方案利用阵列天线生成窄波束对场景进行扫描，MA-CMI可视为压缩感知微波成像，通过控制MA生成多种随机辐射模式构建测量矩阵对场景进行多次测量，其中测量矩阵的每一行都表示一个有效辐射模式[4]。MA-CMI的最大优势在于它仅需要一对收发通道即可，大大降低了系统的硬件成本。根据压缩感知理论，当测量矩阵各列的相关性足够小时，近似保持约束等距条件，可从压缩测量数据中准确恢复稀疏信号[11]。现有的MA主要分为两类：频率分集超材料孔径(Frequency Diversity Metamaterial Apertures, FDMAs)[2,5–8]和动态超材料孔径(Dynamic Metamaterial Apertures, DMAs)[3,4]。FDMAs可以产生高度独立的随频率变化的随机辐射模式，然而这需要FDMA支持较大的工作带宽以获得足够多的有效测量模式。DMAs通过独立控制超材料单元上加载的开关器件的通断状态，进行随机孔径编码获得大量随机辐射模式。基于DMAs的CMI系统不依赖于频率变化，因此其可以工作在单频点下，相比于FDMAs大大节省了频谱资源。

近年来，众多国内外学者对基于MA-CMI系统的成像算法展开了研究。由于MA-CMI可视为压缩感知成像，稀疏信号重构(Sparse Signal Reconstruction, SSR)算法，如正交匹配追踪(Orthogonal Matching Pursuit, OMP)[5]、两步迭代收缩/阈值(Two-step Iterative Shrinkage/Thresholding,TwIST)算法[6]或稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)[7,8]等被用于MA-CMI系统。SSR方法需要将场景区域离散化并假设目标散射中心位于离散网格点上。然而，在实际应用中这一假设通常不能被满足，场景离散化必然造成网格失配使得成像质量变差。针对这一问题，国内外已有许多基于SBL的离网格(Off-grid)误差校正方法。例如，对目标的转向矢量在其邻域网格上进行泰勒近似展开，在此基础上，利用稀疏贝叶斯推理[12,13]、块稀疏贝叶斯推理[14]或多项式求根[15]等方法校正离网格误差。最近，文献[16]提出了一种基于信号子空间匹配的Off-grid波达方向(Direction Of Arrival,DOA)估计方法，文献[17]将该方法应用于MIMO雷达微波关联成像中。然而，在上述所有离网格误差校正的SBL方法中，都要求转向矢量可以用数学公式描述。对于MA-CMI系统生成的随机辐射模式无法用数学公式描述，且MA-CMI是一个单快拍SSR问题。使得上述所有方法都不适用于MA-CMI系统。

本文针对MA-CMI系统测量过程存在离网格误差的情况提出一种基于稀疏贝叶斯学习的Sinc插值离网格成像方法(Off-Grid based on Sinc Interpolation Sparse Bayesian Learning, OGSISBL)方法。首先，第2节针对MA-CMI系统的测量矩阵无法用数学公式表示的问题，提出新的离网格观测模型，其对不在初始划分网格上的散射体的回波数据用2维(Two-Dimensional, 2D)Sinc函数插值逼近在网格上的MA的实测辐射模式。此外，由于Sinc函数的非线性性质，对其执行1阶泰勒展开得到其线性近似式，使得算法的推导易于处理；第3节基于上述观测模型开发了一种具有离网格误差校正能力的成像算法。提出的成像算法基于SBL并在期望最大化(Expectation Maximization, EM)算法框架下迭代消除离网格误差；第4节通过仿真实验对本文提出的成像方法进行验证；第5节为结论。

2 基于超材料孔径计算微波成像系统的观测模型

如第1节所述，MA-CMI系统通过生成多种随机辐射模式探测目标场景，同时接收天线收集场景内目标的回波。将目标场景在2D角域划分均匀网格，网格点坐标矩阵D可表示为

3 2D离网格稀疏贝叶斯学习

3.1 稀疏贝叶斯模型

3.2 稀疏贝叶斯学习(SBL)

根据第2节得到的观测模型。对MA-CMI系统测量结果进行离网格误差校正可描述为如式(18)的最大后验(MAximum Posteriori, MAP)推断问题

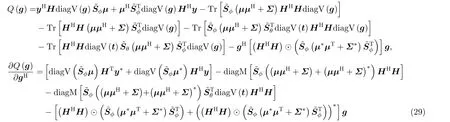
其中，diagM(·)表示取矩阵对角线元素构成列向量，(·)*为共轭算子，(·)H是共轭转置算子。/

算法迭代终止判据由式(32)定义

4 实验仿真与分析

本节通过几个数值模拟实验来验证所提方法的性能。本节的所有成像实验使用的测量矩阵H是通过对一款FDMA-CMI系统在微波暗室环境下采集的辐射方向图数据进行处理得到的。FDMA-CMI系统由FDMA作为发射天线，喇叭天线作为接收天线组成(如图2所示)，此系统的详细设计在本文之前的工作中已给出[20]。图3为34.4 GHz, 36.65 GHz和38.15 GHz频点激励下的FDMA辐射模式图。最终，本文采集得到104种有效辐射模式。文献[21]作为在网(On-grid)模型算法的代表与本文所提算法进行比较，本文中称该算法为On-grid SBL。为了揭示本文所提算法对场景稀疏目标的重构性能，采用均方根误差(Root Mean Square Error, RMSE)作为目标位置的重构性能度量，定义为

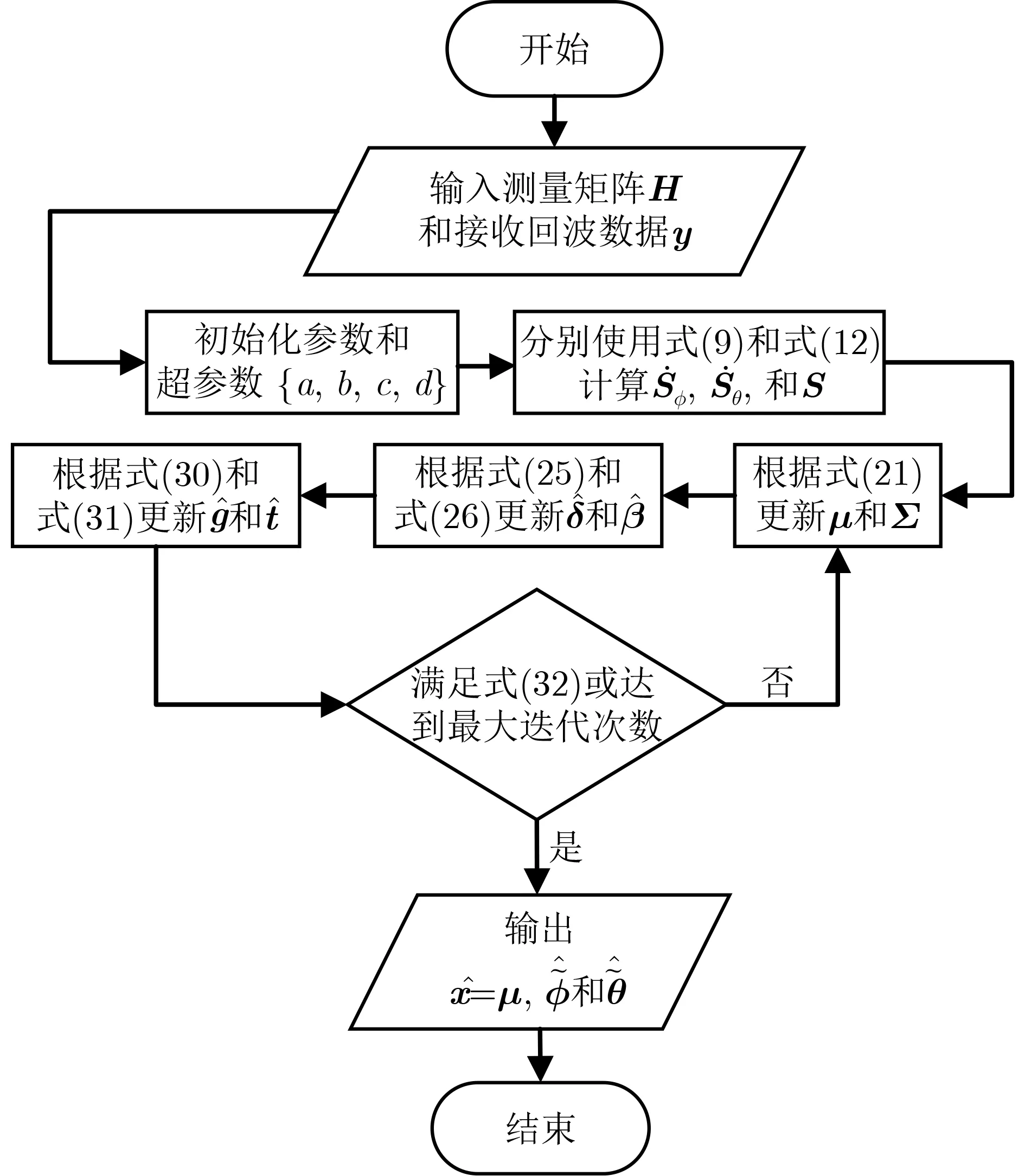
图1 本文OGSISBL算法流程图

图2 FDMA-CMI系统

图3 FDMA在不同频点的归一化辐射模式

实验1 假设一个位于空域xoy平面的目标场景，其 中x ∈[−860 mm, 860 mm],y ∈[−860 mm,860 mm]，FDMA-CMI距离场景500 mm。根据空域与角域的转换关系可知场景在角域的范围为ϕ∈[–60°, 60°]和θ∈[–60°,60°]。将目标场景在角域均匀离散化为31×31个网格点，即俯仰和方位维的网格间距r均为4°。信噪比(Signal to Noise Ratio,SNR)设置为10 dB。为充分证明所提算法对稀疏目标场景的重构能力，本文仿真了3种不同场景，分别是：五边形目标、五角星形目标和雪花形目标。图4显示了本文所提算法与On-grid SBL算法[21]对3种不同场景的重构结果。图4(a1)、图4(b1)和图4(c1)分别为加入随机离网格误差作为扰动后的3种目标场景。其中用红色十字标记散射体的真实位置，而黄色网格标记了散射体所在的初始网格；图4(a4)、图4(b4)和图4(c4)分别为3种场景的真实散射体在空域的归一化幅度。图4(a2)和图4(a5)、图4(b2)和图4(b5)、图4(c2)和图4(c5)分别为3种目标场景的On-grid SBL算法重构结果。可以看出On-grid SBL算法没有更新网格，即该算法不能处理离网格误差，且其成像结果中存在很多高幅度假峰。其中最高假峰的幅度约为0.43，几乎为重构真实目标散射体最低幅度的66%，并且随着场景中目标数量的增加，高幅度假峰的数量也在增加，这在实际应用中是不允许的。本文所提算法对3种稀疏目标场景的重构结果分别如图4(a3)和图4(a6)、图4(b3)和图4(b6)、图4(c3)和图4(c6)所示。由图4(a6)、图4(b6)和图4(c6)可以看出所提方法的重构结果中尽管仍存在假峰，但最高假峰幅度约为0.15，是重构真实目标散射体最低幅度的20%，成像质量得到了很大提高。为了定量分析本文所提算法对离网格误差的校正效果，表1给出了3种稀疏目标场景200次蒙特卡罗实验不同SNR下消除离网格误差的能力。由表1可知，本文所提算法在SNR=20 dB时，3种目标场景的平均离网格误差均可以被减小到初始误差的52.6%左右；即使在SNR=10 dB的情况下，对于场景1的平均离网格误差也可以减小约初始网格的66.0%左右，但随着场景中稀疏目标个数增加算法校正离网格误差的能力略有下降。当SNR=5 dB时，对于3种目标场景，算法均无消除离网格误差的能力，这是由于此时噪声能量可以比拟目标能量。值得注意的是对于场景3，结合图4(c2)和图4(c5)可以看出，On-grid SBL算法失效而本文提出的算法仍然保持很好的重构结果(参见图4(c3)和图4(c6))。

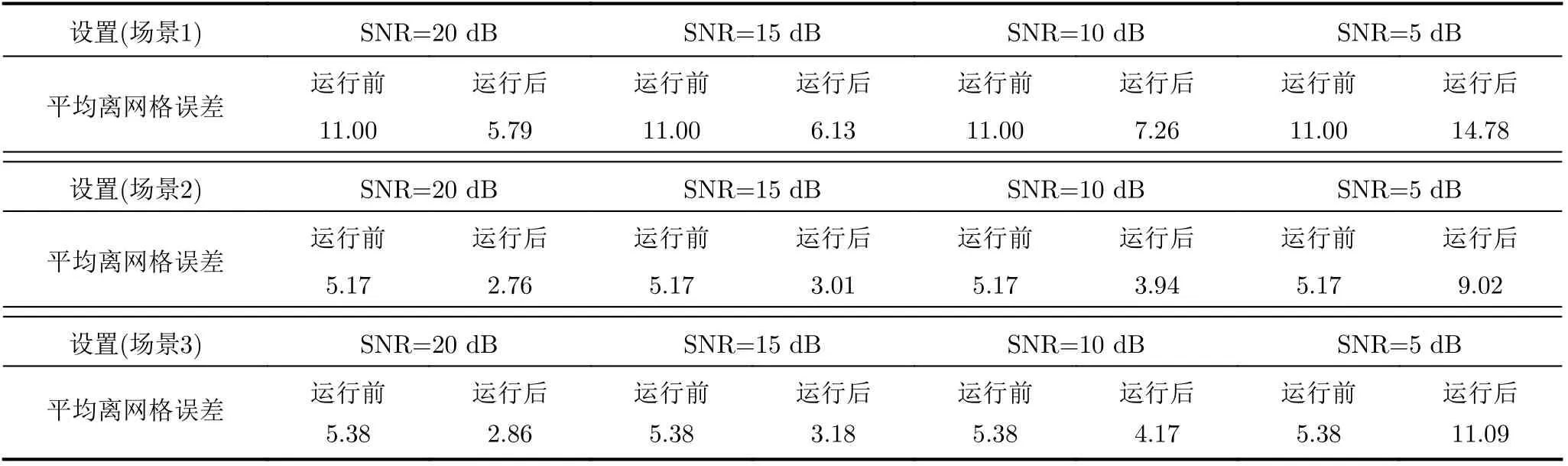
表1 比较不同信噪比下本文所提算法对散射体位置的重构效果(3种不同场景)(mm)

实验2 本实验研究了2种算法对于不同离散网格间隔r随SNR的RMSE变化曲线以及对于不同SNR随离散网格间隔r的算法平均运行时间变化曲线。本实验采用五角星形场景(如图4场景2)，图5(a)为2种算法200次蒙特卡罗实验不同离散网格间隔下RMSE随SNR的变化曲线。从中可以看出2种算法的RMSE均随SNR的增大而减小，且r越小重构性能越好；在SNR为0 dB和5 dB时，无论r取多少，2种算法重构失败；当r一定时，本文所提算法性能始终优于On-grid SBL；当选取相对较粗的网格时，On-grid SBL算法随着SNR提升重构效果并没有明显改善，相比之下，本文提出算法的重构效果大大提升，这是由于本文方法考虑了测量过程中存在离网格误差，并在算法中对其进行了校正，且SNR越高，网格间隔越小，2种算法的重构效果差异越显著。图5(b)为2种算法在不同离散网格间隔r和SNR下的平均运行时间。从中可以看出对于不同SNR，2种算法得平均运行时间均随r的增大快速下降，这是由于当目标场景范围确定时，网格间隔大小直接决定了划分的网格数量，进而决定了计算数据的维度；对于不同网格间隔，On-grid SBL的运行时间始终低于本文所提算法，这是因为On-grid SBL不考虑离网格误差使得其计算量大大降低，但也造成其重构效果很差；当r一定时，2种算法的平均运行时间均对SNR变化不敏感，这说明了网格间隔是影响算法计算效率的主要因素。由图5可知本文所提方法在重构性能与网格间隔间存在反比关系，使得本文方法在实际应用中需要对其进行折中考虑以选取合适的网格间隔。

图5 单快拍、不同信噪比和网格间隔的2种算法的重构性能

5 结束语

本文首先针对MA-CMI系统的测量矩阵是一个伪随机矩阵，无法直接进行数学操作的情况，提出了一种基于2维Sinc插值函数的离网格观测模型。在稀疏贝叶斯学习框架下，基于此观测模型对离网格误差进行校正，获得较好的成像效果，并通过数值仿真验证了本算法的有效性。针对本成像算法的快速算法有待于进一步的研究。