基于等效渗流力法的深埋隧洞围岩稳定性分析

项 勋，任旭华，张继勋

(河海大学水利水电学院，江苏 南京 210024)

0 引 言

近年来，我国西南地区修建了诸多引水隧洞[1]。在实际隧洞施工阶段，由于人类开挖等工程扰动造成洞周渗流场重分布[2]，渗流作用对隧洞围岩稳定不可忽略。因此，研究洞周围岩渗透力分布至关重要。目前，数值计算中渗流力的作用效应有2种反映形式：一是，渗流-应力直接耦合计算，渗流力蕴含于计算结果中；二是，先进行渗流分析，将计算得到的等效渗流力以外力的形式作用于节点上进行间接耦合。针对第2种方法，诸多学者进行相关研究。卢廷浩等[3]提出在土石坝蓄水后采用有效应力加渗流力组合算法进行蓄水后应变分析；何明等[4]采用FLAD3D多孔介质模型结合fish实现渗流应力的间接耦合；朱文炜[5]通过对abaqus二次开发，实现富水区深埋隧洞渗透力的施加，并对比论证渗透力施加的准确性。

在上述研究中，等效渗流力计算的难点在于获取单元节点的水力梯度。鉴于tecplot具有较强的数据分析属性，可轻松实现对总水头3个方向的求导，得到水力梯度的过程。因此，本文采用此方法，计算各单元节点等效渗流力，用算例验证该方法计算渗流-应力耦合的合理性，并依托某富水区深埋引水隧洞，采用该方法进行围岩稳定性分析。

1 等效渗流力提取

渗透水流以动水压力和拖曳力等面力形式作用于土体颗粒上。在实际应用中，通常假定渗透力为体积力[6-7]，公式如下

j=γwi

(1)

式中，i为水力坡降；j为渗透力；γw为水的容重。

对于各项同性岩体，流速、渗流力及水力坡降方向一致。本文中，岩体取各项同性介质，通过渗流分析得到模型孔隙水压力分布，并通过fish语言编程提取单元体的总水头，经接口程序将总水头分布导入到tecplot中，并在x、y、z向求导计算单元体的水力梯度，将梯度数据导出并施加于对应单元上，完成渗流力的施加。

2 算例分析

为验证上述方法的可行性，本文建立模型，分别进行流固耦合计算和等效渗流力法间接耦合计算。模型沿x、y、z向尺寸分别为100、20 m和100 m，洞深50 m。在模型特征位置布置监测路径AB、CD。算例具体尺寸及监测位置见图1。

该算例仅模拟隧洞开挖，未考虑衬砌等结构。开挖前洞周围岩为全饱水层，计算中约束模型底部位移，左右施加法向约束；模型上表面固定孔隙水压力为0，模型底部和左右为不透水边界，伴随隧洞开挖的同时，设置开挖区域为自由透水边界。计算参数见表1。

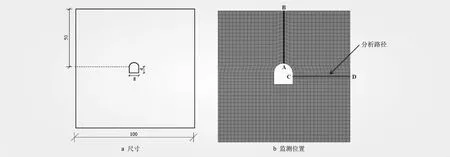
图1 算例具体尺寸及监测位置(单位：m)

表1 计算参数

2.1 变形分析

2种方法得到的毛洞开挖洞周围岩位移变形见图2。从图2可知，2种方法得到的隧洞变形呈现相同规律，均表现为顶拱沉降、底拱隆起，边墙两侧x向位移呈蝴蝶状分布。2种算法计算所得竖向最大沉降值分别为1.22、1.24 mm，最大隆起值分别为0.091、0.104 mm；最大x向位移分别为0.255、0.257 mm。2种算法得到的最大沉降和最大x向位移变形值偏差分别为1.64%和0.78%。

2.2 应力分析

利用等效渗流力进行渗流工况计算时采用土-水分算的方法，以土骨架为研究对象，考虑土体周围的渗透力。由于算例中隧洞处于饱水地层，采用等效渗流力法计算时土体采用浮容重并通过有效应力分析土体应力。流固耦合法的有效应力则通过fish语言编程遍历单元获取单元的最大、最小主应力并减去单元的孔隙水压力值获得。

2种算法计算得到的围岩有效应力见图3。从图3可知，2种算法下主应力分布规律一致，均表现为边墙位置小主应力腰果状分布，拱顶和拱底主压应力较小。洞周最大主压应力分别为2.51 MPa和2.47 MPa，洞周最大主应力均为负值，表明洞周围岩处于三向受压状态。本文限于篇幅，在后续分析中仅考虑洞室周边最小主应力分布。

2.3 分析路径对比

沿路径AB、CD分别提取2种算法下围岩应变规律，结果见图4。从图4可知，2种算法得到的AB和CD特征路径上的应力变形规律基本一致。在CD路径上，同位置节点x向位移最大偏值仅为0.03 mm，最大偏值出现于C点，偏离程度为11.7%。随着距离洞周边墙C点越远，隧洞向开挖面变形逐渐减小并趋于稳定。2种算法得到的洞周围岩整体规律和数值大小十分契合，由此可以论证，采用等效渗流力法计算渗流工况的合理性。

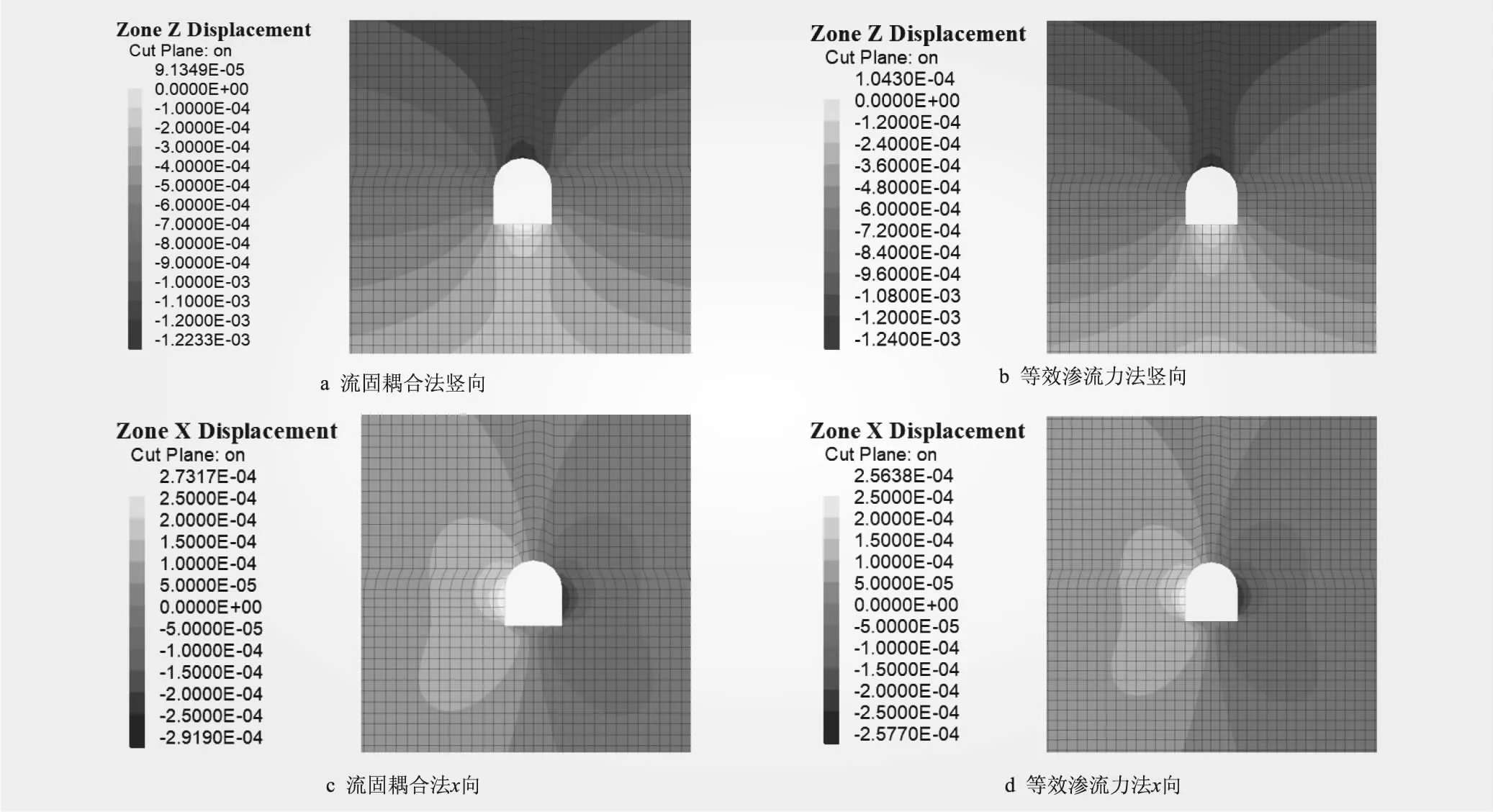
图2 2种算法下毛洞开挖洞周围岩位移变形(单位：m)

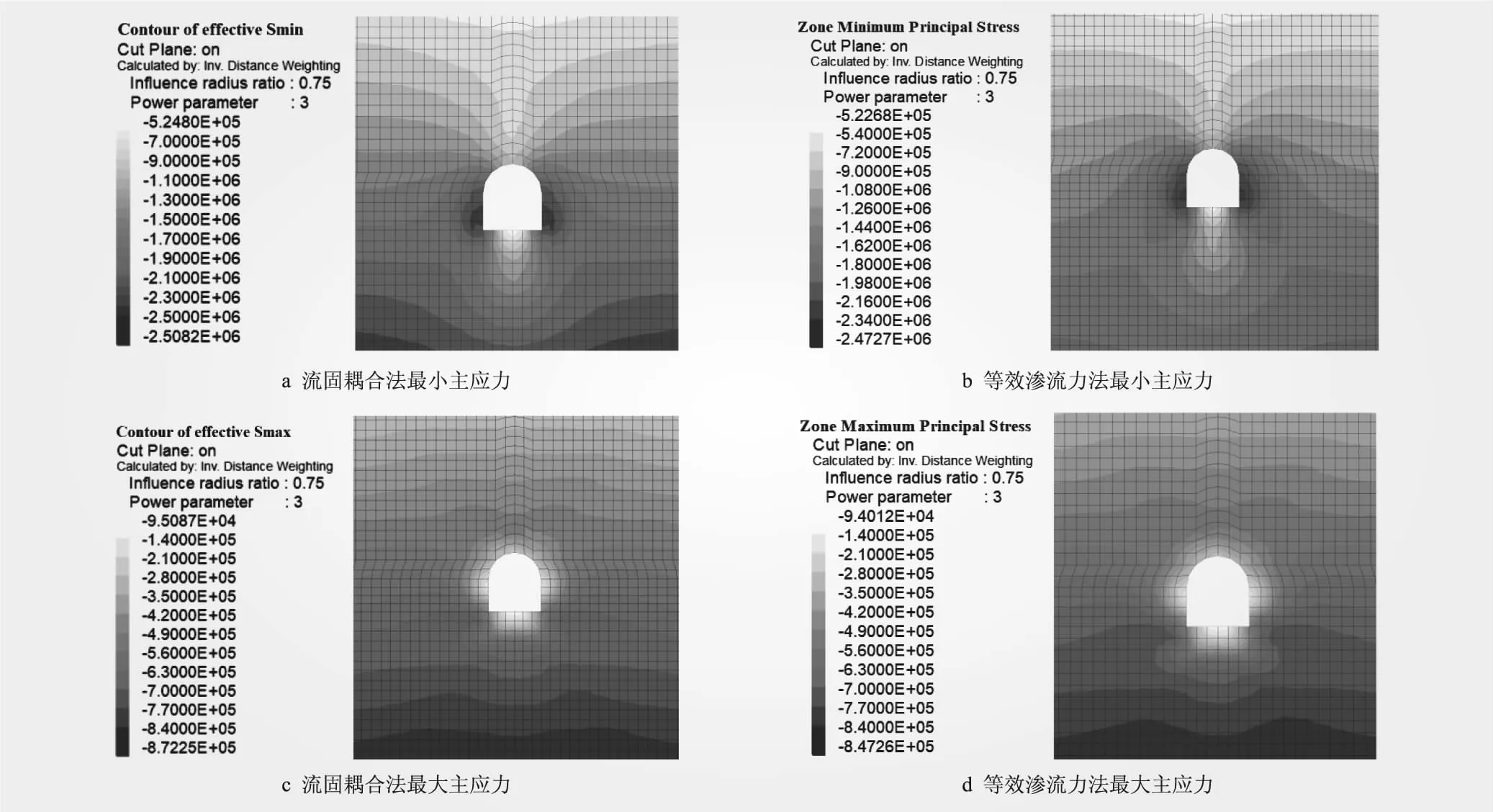
图3 2种算法下毛洞开挖洞周围岩主应力(单位：Pa)

图4 2种渗流工况下毛洞开挖围岩应力变形对比

3 工程实例

某电站引水隧洞群由4条长约16.7 km的圆形隧洞组成。1号隧洞15+200断面埋深1 300 m，所处地应力约为33 MPa。为降低衬砌高外水压，该工程采用注浆+排导的堵排结合方式，灌浆圈厚度为6 m，在洞周均匀布置12个减压孔用于排水。

3.1 计算模型及材料参数

为简化计算，本文选取典型断面15+200断面进行计算。模型沿洞中向上、向下各取150 m，左、右距隧洞边界100 m，灌浆圈厚度为6 m，在每个隧洞周边均匀布置12个减压孔，模型顶部施加33 MPa的面荷载模拟上部地应力作用。在纯渗流计算时，模型顶部施加固定100 m水头，开挖区域赋予流体空模型。模型整体及细化结构见图5。模型力学及渗流参数见表2。

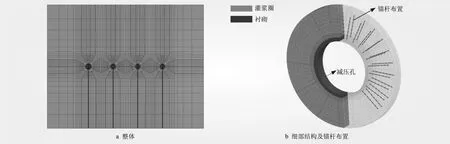
图5 计算模型

表2 数值计算材料参数

3.2 计算结果

3.2.1 渗流场分析

1号隧洞衬砌外水压力分布见图6。从图6可知，灌浆圈范围内孔隙水压力得到一定程度的降低，且减压孔的设置使得附近地下水排出，孔隙水压力消散显著，在距离减压孔较远范围水压降低效果不佳。衬砌最大外水压力为1.40 MPa，出现于未设置减压孔的底拱位置，在减压孔周围衬砌外水压力很小。经堵排结合方式处理后，作用于衬砌的高外水压力显著降低，衬砌局部应力得到有效改善。

3.2.2 应力变形分析

为考虑隧洞开挖卸荷后施加支护的过程，采用围岩应力释放60%后施加衬砌和锚杆支护模拟。等效渗流力计算1号隧道开挖支护后，围岩变形见图7。从图7可知，经喷锚支护后，洞室呈现顶拱沉降、底拱隆起、边墙向洞内变形的基本规律。洞周最大沉降位移为25.17 mm，出现于顶拱位置，最大隆起值为12.76 mm，出现于底拱位置；x向位移形如蝴蝶状分布，最大位移为5.65 mm。

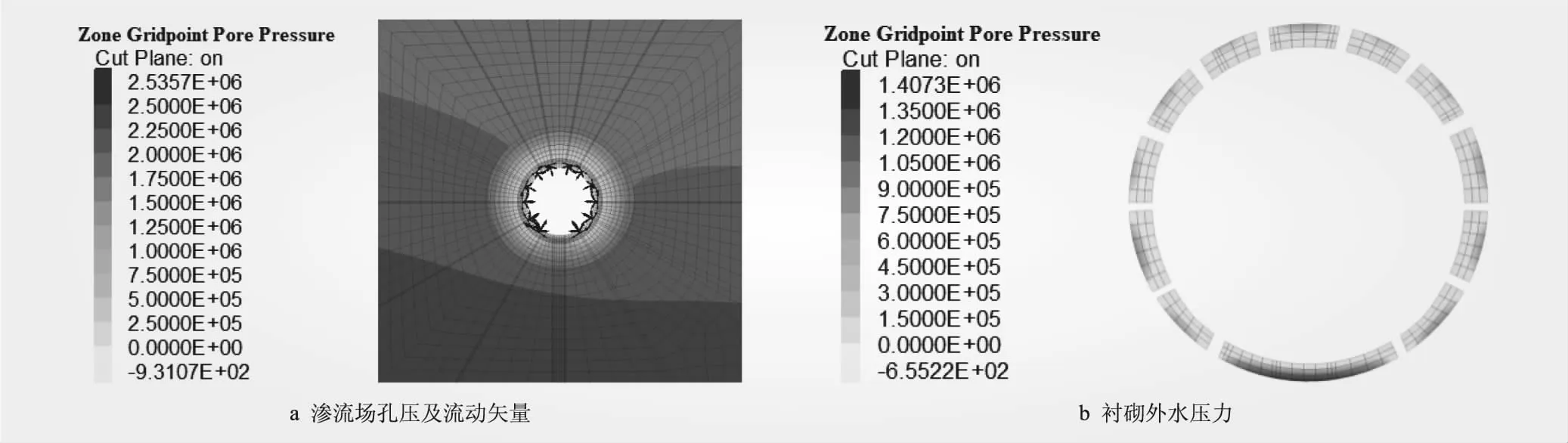
图6 1号隧洞衬砌外水压力分布(单位：Pa)

图7 等效渗流力计算1号隧道开挖支护后围岩变形(单位：m)

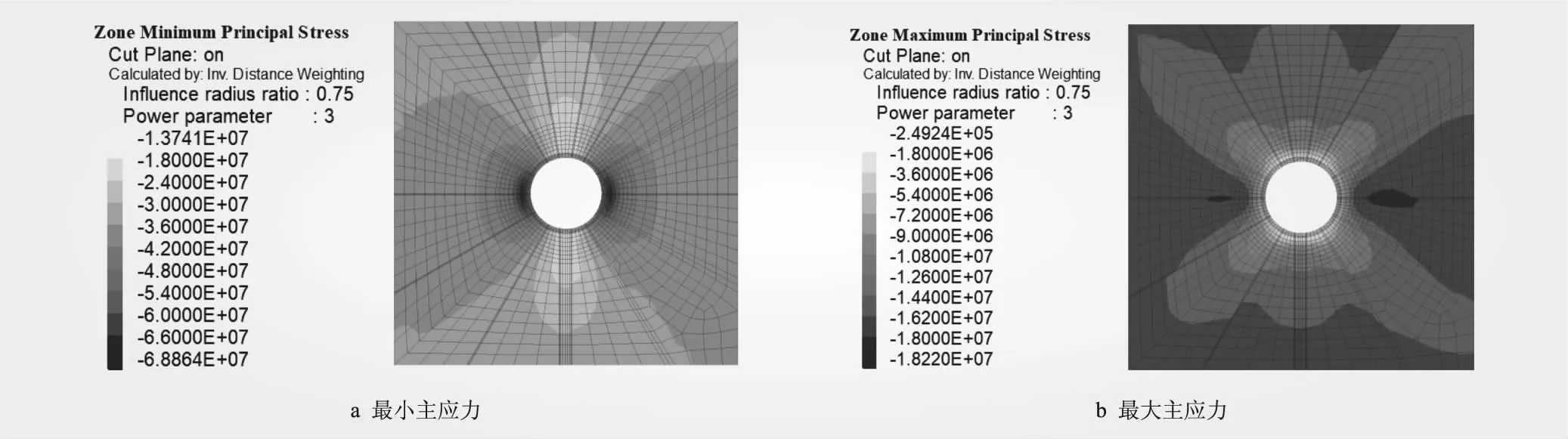
图8 等效渗流力计算1号隧洞开挖支护围岩主应力(单位：Pa)

采用围岩收敛应变率(隧洞最大变形量与1/2开挖跨度之比)作为洞室围岩稳定状态指标，该洞室经喷锚支护后最大收敛应变率为5.61‰，小于围岩变形稳定界限值2%[8]，可认为该隧洞不会因为变形过大而导致围岩失稳。

等效渗流力计算1号隧洞开挖支护围岩主应力见图8。从图8可知，随着洞室的开挖，围岩周边局部范围产生扰动导致应力重分布，洞周围岩主压应力呈纺锤体状分布，距侧墙一定深度位置出现明显的应力集中区域，最大主压应力为68.9 MPa；同时，由于洞周应力的释放，靠近临空面主压应力值较小，且相较于侧墙位置，顶拱和底拱位置应力释放更加明显，顶拱和底拱位置最大主压应力约为13～16 MPa。洞周主拉应力均为负值，表明该隧洞围岩3个方向均处于受压状态，围岩整体受力良好。

4 结 语

本文通过算例，对比等效渗流力法和流固耦合法计算渗流工况洞周围岩特征路径上的应变分布规律，验证了等效渗流力法的有效性和合理性，并采用该方法对某富水区深埋隧洞进行围岩稳定性分析，得到如下结论：

(1)通过tecplot数据分析功能，可方便有效地获取整体模型水力梯度分布；通过编制fish程序施加等效渗流力可间接耦合渗流计算，且计算结果表明该算法准确有效，概念清晰便于理解。

(2)减压孔的设置对于改善孔口周边孔隙水压力具有显著效果，但同时减压孔的存在会破坏衬砌的整体性，在隧洞建设中应综合考虑，采用合理的减压孔布置方案。

(3)对于高外水高应力深埋引水隧洞，堵排结合的方式能有效降低衬砌外水压力，可维持衬砌正常工作和改善衬砌应力水平。