在复习“旧知”中经历“新知”生长——“长方体和正方体的表面积与体积”复习课的前思后想

■ 钱 蔚

教学“长方体和正方体的表面积与体积”这一单元的复习课时，我们要经常思考这些问题：复习什么？怎么复习？为什么这么复习？复习课的打开方式绝不是“炒冷饭”，更不是“题海战”。如何让学生透过复习这扇窗看到一个全新的数学世界，真正体验复习的价值呢？伴着这样的思考，笔者谈谈教学“长方体和正方体的表面积与体积”复习课的前思后想。

一、观察与想象，学生自主建构长方体和正方体的直观表象

【课前思考】

“长方体和正方体的表面积与体积”是“空间与图形”这一领域较重要的一个单元，通过这一单元的学习，学生应进一步积累空间与图形的学习经验，进一步发展和增强空间想象力。怎样发展学生的空间想象力呢？笔者认为，首先，我们必须清楚地知道什么是空间想象力。具体地说，空间想象力是指在头脑中能正确反映出事物的空间形式，包括物体的形状、大小、位置关系等。从心理学角度看，这也是指我们能够依据感觉经验，在头脑中正确建构起物体的直观表象。为此，笔者认为，教学中的每一个环节都要充分考虑如何为发展学生的空间想象力而设计。

【教学片段1】教师出示小棒图（如图1）。

图1

师：请同学们仔细观察图1，想一想，取这些小棒可以搭一个长方体吗？如果可以,怎么搭？（在学生回答后教师依次出示图2至图4）

图2

图3

图4

【课后反思】课始，教师没有直接将长方体物体或长方体框架呈现在学生面前，而是出示凌乱的12根小棒(如图1)，让学生在头脑中搭一个长方体，此任务的提出具有一定的挑战性，从学生课堂的反映可以看出，这一环节设计达到了两个目的：1.“盘活”了学生头脑中的“库存”，促使学生主动回忆长方体的面、棱、顶点的特征；2.让学生在观察与想象的任务驱动中调动知识和经验，完成了在头脑中的物体拼搭过程。引导学生有效地经历了数学化的过程，在一定程度上培养了学生的空间想象能力。

如果教师直接提供完整的长方体物体或框架，可以开门见山揭示课题，节省课堂教学时间，但是这样的开场如“清汤寡水”，吸引不了学生，学生也不可能经历观察与想象这一过程，长方体的特征这一知识仅凭“温暖的回忆”只能起到“知识的重现”这一目的，而使之通过想象活动来完成，学生在头脑中尝试着将12根小棒排列、组合、拼搭，脱离了具体的操作，也许一些学生会有些困难，但只有在这样的想象活动中才能“盘活”知识，发展学生的空间想象能力。

二、整理与交流，学生自主梳理长方体和正方体的知识体系

【课前思考】

整理知识、交流知识是复习课的重要特征，这也是它有别于练习课和新授课之处。常见的复习课，师生通过一问一答的形式由教师将知识整理出来。笔者认为，整理知识要让学生自主进行，为了让学生有充裕的时间自己整理，寻找知识间的联系与区别，也为了提高复习课的效率，可以放至课前、课中来交流与巩固。

【教学片段2】

师：昨天，同学们回家自己进行了长方体和正方体相关知识的复习，请拿出复习单，我们一起来交流。

根据学生的回答，教师完成表格内容（如表1），为了使学生更清楚地复习长方体和正方体的表面积与体积的计算方法，教师还可以利用课件帮助学生回忆长方体和正方体的展开图和体积公式的推导过程。

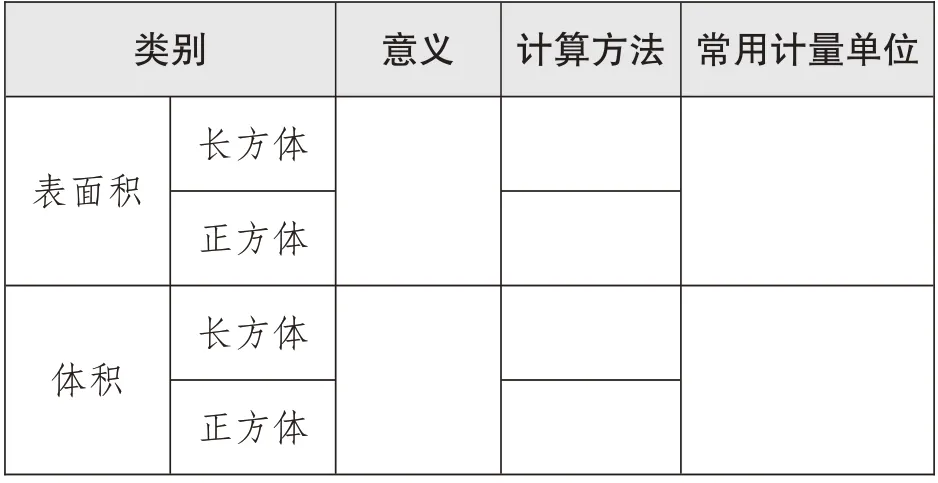
表1

师：通过复习我们发现长方体和正方体在哪些方面是有区别的？

生：长方体和正方体的表面积与体积的意义不同，计算方法不同，计量单位也不一样。

师：是的，表格能让比较一目了然，所以在运用时，我们要看清楚求什么，想明白怎么求。请看下面这些问题，它们与长方体或正方体的什么知识有关？

1.填满花坛大约需要多少立方米泥土？

2.粉刷教室四壁和顶部。

3.包装长方体纸盒需要彩纸多少张？

4.一个长方体书柜能装多少本书？

5.给长方体饼干罐的四周贴一圈商标纸。

6.包扎一个长方体纸盒需要多长的包装带？

7.鱼缸占地面积是多少？

【课后反思】

知识的整理与建构要凸显学生学习的自主性，让学生试着自己去把知识纵向成线、横向成片，在“做”中形成良好的认知结构，在“做”中学会整理知识的方法，以积累整理建构的经验。

在上述教学片段中，整理知识是学生课前的任务，课中在教师的组织下，学生积极快速地进行交流，教师只在关键处提醒、点拨。比如：长方体的体积是如何推导出来的？除了这个公式，长方体的体积还可以怎么求？长方体的表面积与体积之间的区别在哪里？此时，课堂完全交给学生，学生参与的积极性非常高，效果也很好。针对解决实际问题中学生对于表面积与体积的混淆，教师出示了一组判断题，既达到了巩固知识、查漏补缺的目的，又凸显了物体具有线、面、体三维空间的特性，帮助学生在知识的大框架下构建知识体系，找到知识间的联系与区别。

三、练习与拓展，学生自主探索解决问题的方法与策略

【课前思考】

教师在复习课中要重视练习与实际应用，既有利于知识的巩固和内化，也有利于发展学生思维，提升应用能力。但如果复习课演变成为“炒冷饭”，做题目，那么这样的复习课，有效性是要打问号的，也不能激发学生的学习兴趣。在复习课中我们要进行基础题的相关练习，更要设计一些具有挑战性的习题引领学生探究、思考、争辩、创新，尤其要在练习的过程中渗透数学思想方法。因此，备课时教师要反复思考如何设计练习，用心设计适合本班学生的习题。

【教学片段3】

1.如图5，一个长方体的长是6厘米，宽是3厘米，高是3厘米，这个长方体的侧面积是多少平方厘米？

图5

第一层次：学生计算。

第二层次：教师引导学生想象侧面展开图，拓展侧面积的另一种计算方法：底面周长×高（如图6）。

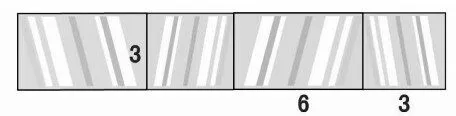
图6

第三层次：小结。

师：同学们，我们是怎样得到侧面积的计算方法的？

生：通过想象，画出图形后，得到了侧面积的另一种计算方法。

（教师板书：展开想象，画出草图）

2.如图7，一个长方体的底面是面积为100平方厘米的正方形，它的侧面展开图正好是一个正方形，这个长方体的表面积是多少平方厘米？

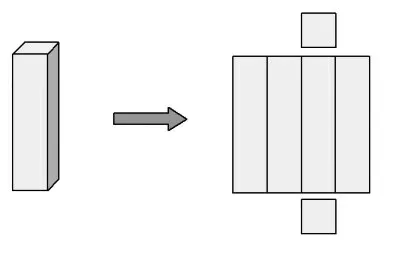
图7

第一层次：小组讨论，画图发现长方体的底面边长是10 厘米，展开图边长是40 厘米，可以求出表面积。

第二层次：改变底面积数据，100平方厘米改为300平方厘米。

第三层次：再次改变底面积数据，300平方厘米改为a平方厘米。

3.学校总务主任做了一个台阶的模型，要求大家帮忙算算，体积是多少？

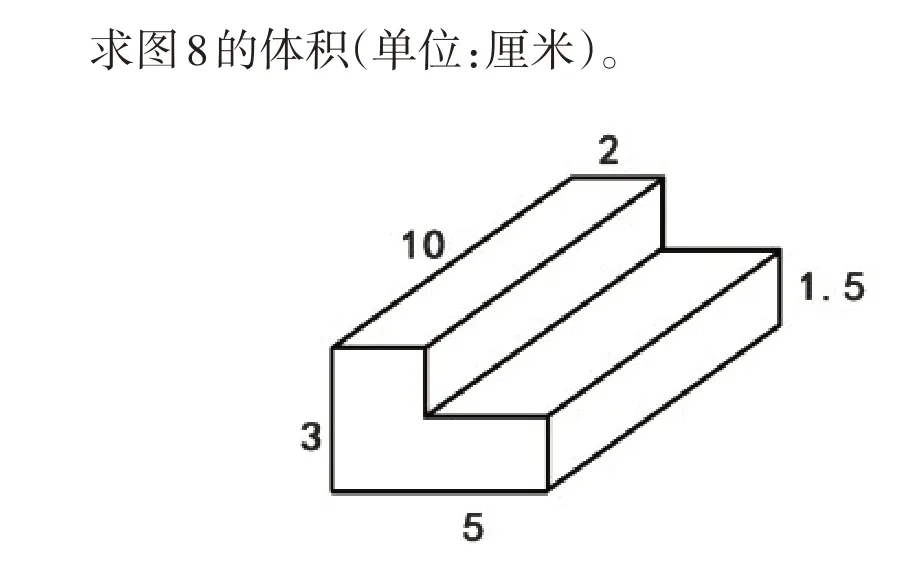
图8

生：可以把这个台阶分成两个长方体，再把它们的体积相加。

（学生上台添加辅助线，将台阶分成长、宽、高分别为10 厘米、5 厘米、1.5 厘米和10 厘米、2 厘米、1.5厘米的两个长方体）

师：还可以怎样分？

（学生跑上台又添了一条辅助线，将台阶分成长、宽、高分别为10 厘米、3 厘米、2 厘米和10 厘米、3厘米、1.5厘米的两个长方体）

生：还能先把这个台阶补成一个长方体，长是10厘米，宽是5厘米，高是3厘米。再减去一个长方体，长是10厘米，宽是5-2=3（厘米），高是1.5厘米。

生：我觉得分好后还可以拼在一起，就变成一个长方体了，这个长方体的长是10 厘米，宽是5+2=7（厘米），高没变，还是1.5厘米。

生：我想明白了，就是先分后移，这样是可以拼成一个长方体，算起来也简单了。

……

【课后反思】

这组练习题由浅入深、由易到难，充分体现了“不同的人在数学上得到不同的发展”的要求。

第1 题的第一个层次是基本题训练，是每个学生都能达到的基本要求。第二个层次，我们意图拓展侧面积的思考路径，拓展学生的思维空间，也为即将学习圆柱体的侧面积埋下伏笔，渗透立体图形知识。第三个层次，进行适时小结，帮助学生提升解题水平。

第2 题也有三个层次，第一个层次是“展开想象，画出草图”这一策略的活学活用，让学生画出图形，根据图形思考，发现一个正方形的面积是100平方厘米，正方形的边长就是10 厘米，从而找到大正方形的边长是40 厘米，顺利求出长方体的表面积。第二个层次改变数据，100平方厘米改为300平方厘米，300 平方厘米不是某个数的平方，用现有的经验求不出底面的边长，怎么办？遇到新问题，寻求新思路，逐步提升学生的思维层次，培养学生思维的灵活性和变通性。第三个层次用字母来表示底面积，由具体到抽象，逐级而上，培养了学生的抽象思维能力。

第3题是求不规则物体的体积。解决这个问题必须综合运用体积的相关知识。学生通过观察，用切分相加、先补后减的方法顺利求出了这个物体的体积。

总而言之，在复习课教学中，我们要将分散的知识点合理归并，整体呈现，突出知识间的内在联系和本质区别。在整合知识的基础上设计发展思维能力的习题，促使学生在“旧知”的复习中经历“新知”的生长。