某液压打桩锤专用组合插装阀的建模与仿真*

孙灿兴,黄 增,任 旺,王 琳,付承伟,孔祥东,楼申琦

(1.上海海岳液压机电工程有限公司,上海 200000;2.燕山大学 机械工程学院,河北 秦皇岛 066004;3.中信重工机械股份有限公司 洛阳矿山机械工程设计研究院,河南 洛阳 471003)

0 引 言

二通插装阀是一种以二通型单向元件为主体,采用先导控制和插装式连接的新型液压控制元件,具有抗污染能力强、工作可靠、结构简单、流动阻尼小、通流能力大,以及可实现方向、流量、压力等多种控制功能等优点。由于其具有特别适用于高压大流量系统、组合方式灵活的特点,在液压系统中得到了广泛应用[1-5]。

与某液压系统回路环形阀组配套使用的专用高品质组合式插装阀是设备的核心元件,要求具有大流量、快速响应、耐冲击等特性。目前,国内产品与国外相比还存在较大差距,相关技术为国外公司垄断,产品供货周期和造价、维护、备品等均受制于人,亟需突破垄断,做到自主可控。

随着流体力学、算法理论、可靠性理论等学科的发展,特别是在计算机技术飞速发展的今天,流体仿真技术也日益成熟,越来越成为液压设计人员强有力的辅助工具[6]。计算机仿真技术已经成为现代高科技产业中不可或缺的进行系统分析的一项关键性技术手段[7]。

张晋等人[8]对插装阀压力和温度变化引起的油液密度和黏度的变化规律进行了研究,在考虑了摩擦力与伺服阀阀口流量的基础上,对其先导部分与主阀部分进行了机理建模,从而提高了模型的准确性。张威[9]通过对二通比例流量阀工作原理的分析,考虑了其负载特性,利用仿真软件AMESim建立了相应的液压模型,并对其进行了动态仿真,研究了二通比例流量阀的动态特性。杨亦婷等人[10]对某电磁阀的工作原理、磁场特征、运动过程等进行了分析,采用磁路分析法建立了其动态过程的数学模型,利用Simulink进行了电磁阀动态过程仿真,针对电磁阀主要参数,对动态响应特性的影响进行了研究。YUE Da-ling等人[11]利用计算机建模,针对脉冲电压持续时间,对螺杆式插装阀启闭动态特性的影响进行了研究。WANG Wen-zhu等人[12]利用AMESim对二通比例插装阀的建模与仿真进行了研究。

为了对液压打桩锤的组合插装阀动作过程中的响应特性和流场特性进行研究,笔者在总结前人研究的基础上,通过考虑弹簧刚度、阀芯各面所受压力、稳态液动力、阀芯重力、液体阻尼力等因素对阀芯动作特性的影响,建立插装阀的动态响应数学模型,并利用AMESim和Fluent软件进行仿真研究。通过获取特定条件下插装阀的性能参数、快速响应数据和可靠性数据,为整机的可靠性分析及性能预测提供重要依据。

1 插装阀结构及工作原理

1.1 插装阀结构

该插装阀结构如图1所示。

图1 插装阀结构示意图

该插装阀主要包括盖板、弹簧座、弹簧、阀芯、阀套等部件。

1.2 插装阀的工作原理

液压打桩锤专用插装组合阀的原理如图2所示。

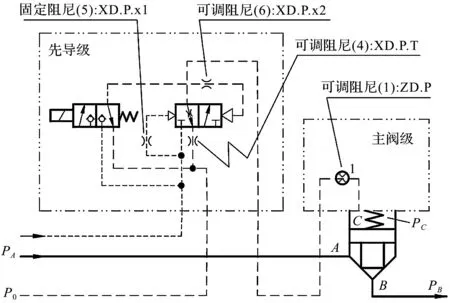
图2 插装阀工作原理图

液压打桩锤专用组合阀系统由两部分组成,包括先导级和主阀级。其中,主阀为插装阀(之所以选择插装阀,是为了能够满足海上作业打桩锤大流量的需求)。高压油从A口流入,B口流出,控制口C控制插装阀的开启与关闭。

先导阀主要由两部分组成,包括电磁阀和二位三通液控换向阀。在电磁阀未得电的情况下,阀芯处于右位,高压油pA无法通过电磁阀控制液控换向阀,此时液控换向阀右端处于低压状态,高压油pA进入液控换向阀左端,推动换向阀右移,所以换向阀处于左位,主阀的控制腔内液压油通过换向阀,回到低压油箱p0,此时控制腔pC为低压,主阀阀芯受A、B面向上压力而向上移动,主阀B口和A口连通,主阀开启;相反,当电磁阀得电的时候,阀芯移到左位,液控换向阀右侧压力升高,推动换向阀左移,换向阀处于右位,高压油pA进入主阀控制腔C,推动主阀阀芯下移,从而主阀关闭。

1.3 插装阀的技术参数

插装阀的主要技术参数如表1所示。

表1 插装阀的主要技术参数

2 插装阀数学模型的建立

在插装阀的仿真研究中,准确建立插装阀的数学模型是难点。

插装阀的工作过程涉及到液压油压力、阀芯重力、稳态液动力[13]、弹簧力、液体阻尼力、侧向力[14]等多种力的耦合作用,阀芯受力的数学模型由流量方程、流量连续性方程和阀芯的力平衡方程组成。

2.1 电磁阀建模

先导阀的电磁驱动力与驱动电压成比例关系,故可等效为一个比例环节。阀芯位移与输入电压信号之间的传递函数可以简化为:

(1)

式中:xV—先导阀阀芯位移,mm;UV—输入电压,V;Ka—阀功率放大器增益;KV—伺服阀增益;wf—伺服阀固有频率;ζm—伺服阀阻尼比。

2.2 液控换向阀建模

液控先导阀流量方程为:

q1=Kqxt-Kc(p2-p0)

(2)

式中:Kq—流量增益;Kc—流量-压力系数;q1—控制流量,L/min;p0—油箱压力,MPa;p2—换向阀阀背压,MPa。

液控先导阀运动方程为:

(3)

式中:xt—液控先导阀位移,mm;mt—液控先导阀阀芯质量,kg;pA—供油压力,MPa;AD—液控先导阀左侧面积,mm2;AE—液控先导阀右侧面积,mm2。

2.3 插装阀开启过程数学建模

2.3.1 阻尼孔通流方程

若不考虑管道中的液体压缩,开启过程阻尼孔的通流方程为:

(4)

式中:Cd1—1号阻尼孔流量系数;Cd4—4号阻尼孔流量系数;A1—1号阻尼孔通流面积,mm;A4—4号阻尼孔通流面积,mm;pC—插装阀控制腔压力,MPa;p2—液体通过1号阻尼孔后管路压力,MPa。

2.3.2 流量连续性方程

开启过程中的流量连续性方程为:

(5)

式中:x—插装阀阀芯位移,mm;AC—插装阀C面面积,mm2;VC—插装阀控制腔体积,mm3;Cip—插装阀内泄漏系数;K—液压油有效体积弹性模量。

2.3.3 稳态液动力

由于流体的运动状态通常比较复杂,很难通过精确的数学表达式来表示其速度和压力的实际分布,因此,不能够应用积分的方法来计算稳态液动力。可以应用动量定理,通过求解所选控制体的动量变化,反求阀芯所受液动力[15]。

由动量定理得:

Fsdt=ρv2Acosαdt

(6)

式中:Fs—流体轴向液动力,N;v—流体轴向流速,m/s;ρ—液压油密度,kg/m3;α—射流角度,45°。

又因流量公式:

q=Av

(7)

并将式(6)两边同时对时间积分,可得:

FS=ρqvcosα

(8)

锥形阀口过流速度为:

(9)

锥形阀口过流面积为:

(10)

插装阀阀口流量为:

(11)

将式(9,11)式代入式(8),可得稳态液动力为:

(12)

稳态液动力刚度为:

(13)

式中:CV—速度系数,一般取0.95～0.98;Cd—插装阀流量系数;d—插装阀出口直径,mm;pA—插装阀A面压力,MPa;pB—插装阀B面压力,MPa。

2.3.4 主阀芯的运动平衡方程

开启过程主阀芯的运动平衡方程为:

(14)

式中:AA—插装阀A面面积,mm2;AB—插装阀B面面积,mm2;m—插装阀阀芯质量,kg;B—主阀芯的黏性阻尼系数;k—弹簧刚度,N/mm。

2.4 插装阀关闭过程数学建模

2.4.1 阻尼孔通流方程

若不考虑管道中的液体压缩,关闭过程阻尼孔的通流方程为:

(15)

式中:pA—控制口高压/供油压力,MPa。

2.4.2 流量连续性方程

关闭过程中的流量连续性方程为:

(16)

2.4.3 主阀芯的运动平衡方程

关闭过程主阀芯的运动平衡方程为:

(17)

2.5 仿真模型参数

仿真模型参数如表2所示。

表2 仿真模型参数

3 插装阀仿真模型的建立与分析

电磁阀建模部分解释了输入电压信号与阀芯位移之间联系;液控先导阀建模部分解释了液控先导阀位移与控制流量之间的联系;插装阀部分数学建模分别列出了阻尼孔通流方程、流量连续性方程和主阀芯的运动平衡方程,从而得到了控制流量引起阀芯位移变化之间的联系。

以上数学建模将输入电压信号与阀芯位移变化关联起来,准确解释了插装阀的工作原理。

通过设置数学模型中的相关参数,再利用AMESim软件,笔者搭建先导级与主阀级的仿真模型,并进行计算。

笔者所建仿真模型如图3所示。

图3 先导级与主阀级的仿真及测试模型

通过AMESim建模仿真,可得到插装阀控制腔压力仿真曲线,如图4所示。

图4 控制腔压力仿真曲线

图4中,在0 s时,控制管路联通低压p0,控制腔C内的压力迅速下降到0 Pa。5.7 s后,控制管路联通供油压力高压pA,控制腔内的压力迅速上升至25 MPa。

控制腔内压力的变化控制插装阀的运动状态。

插装阀的主阀位移的动态响应特性仿真曲线,如图5所示。

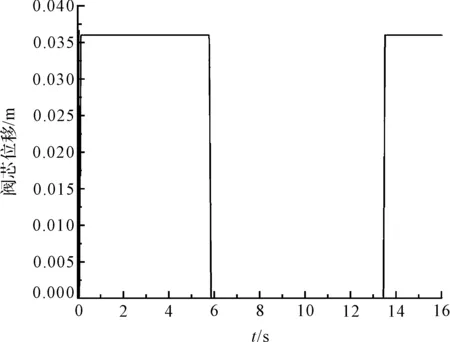
图5 阀芯位移仿真曲线

图5中,控制管路联通油箱低压时,控制腔内的压力迅速下降到0 Pa,此时插装阀C面所受压力为0,插装阀芯A、B面受液体向上的压力而向上运动,到0.036 m处停止;控制管路联通高压时,控制腔内的压力迅速上升到25 Pa,此时插装阀C面受到较大压力,推动插装阀芯向下运动,直至插装阀完全关闭。

插装阀芯的上下运动直接导致插装阀的开启与关闭,从而控制液体流动。

插装阀开启与关闭过程中,插装阀入口处的压力变化如图6所示。

图6 插装阀入口压力变化图

图6中,插装阀开启瞬间,入口与出口连通,入口压力迅速下降到15 MPa;插装阀关闭瞬间,入口与出口断开,入口压力又上升到25 MPa。

插装阀开启与关闭过程中,插装阀出口处的压力变化如图7所示。

图7 插装阀出口压力变化图

由图7可知:由于负载压力恒定,所以出口处的压力稳定在16 MPa。

插装阀开启与关闭过程通过插装阀的流量变化,如图8所示。

图8 插装阀口流量仿真曲线

由图8可知:在插装阀开启瞬间,由于插装阀入口压力为25 MPa,出口压力为15 MPa,插装阀两侧存在较大压差,阀口流量跃升至33 000 L/min,之后入口压力逐渐降低,流量稳定在5 000 L/min;当插装阀关闭时,阀口流量迅速减小为0。

4 主阀流场分析

由于插装阀结构复杂,理论计算过程中,很多问题都被简化忽略了,其计算结果比较粗略。

采用计算流体动力学方法,则能更精确地得到插装阀内部的流场特性。因此,笔者采用计算流体动力学的方法,对不同开度时插装阀腔内的流场进行稳态仿真,得到插装阀腔内流体流动区域的流量特性、速度分布和压力分布情况。

4.1 流体域模型

插装阀模型如图9所示。

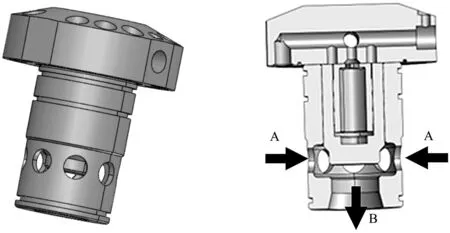
图9 插装阀模型

当阀芯向上运动时,插装阀打开,液体由A口进入插装阀,从B口流出。当阀芯向下运动时,插装阀关闭。

笔者将插装阀模型(采用Solid works建立)转换为x-t格式,之后将其导入到Fluid Flow(Fluent)软件中,根据流体在阀套内流过的区域,提取出流体域用于流场分析;

笔者将流体域模型设为进油口inlet、出油口outlet和壁面wall 3部分,采用Fluent自带的Meshing功能进行网格划分,减少了网格的生成时间,简化模型和网格生成的过程[16-18],最终得到的流体域模型网格划分。

流体域抽取与网格划分如图10所示。

图10 流体域抽取与网格划分

流体域模型网格划分中的总网格数为507 535,总节点数为97 449。笔者检查网格质达到0.830 01,符合仿真分析要求;检查网格平均扭曲度为0.238 52,符合仿真分析要求。

P阀总行程为36 mm,笔者分别取阀芯开度为20%、40%、60%、80%、100%进行流场分析,根据不同开度时的实际工况,得出三维和二维仿真云图,进而对比流速云图、压力云图的变化情况。

4.2 仿真结果分析

阀口开度为20%即7.2 mm时,出口平均流速为19.64 m/s,三维的速度和压力云图如图11所示。

图11 三维云图(20%开度)

二维的速度和压力云图如图12所示。

图12 二维云图(20%开度)

阀口开度为40%即14.4 mm时,出口平均流速为39.20 m/s,三维的速度和压力云图如图13所示。

图13 三维云图(40%开度)

二维的速度和压力云图如图14所示。

图14 二维云图(40%开度)

阀口开度为60%即21.6 mm时,出口平均流速为53.22 m/s。三维的速度和压力云图如图15所示。

图15 三维云图(60%开度)

二维的速度和压力云图如图16所示。

图16 二维云图(60%开度)

阀口开度为80%即28.8 mm时,出口平均流速为55.44 m/s。三维的速度和压力云图如图17所示。

图17 三维云图(80%开度)

二维的速度和压力云图如图18所示。

图18 二维云图(80%开度)

当阀口开度为100%即36 mm时,出口平均流速为57.28 m/s。三维的速度和压力云图如图19所示。

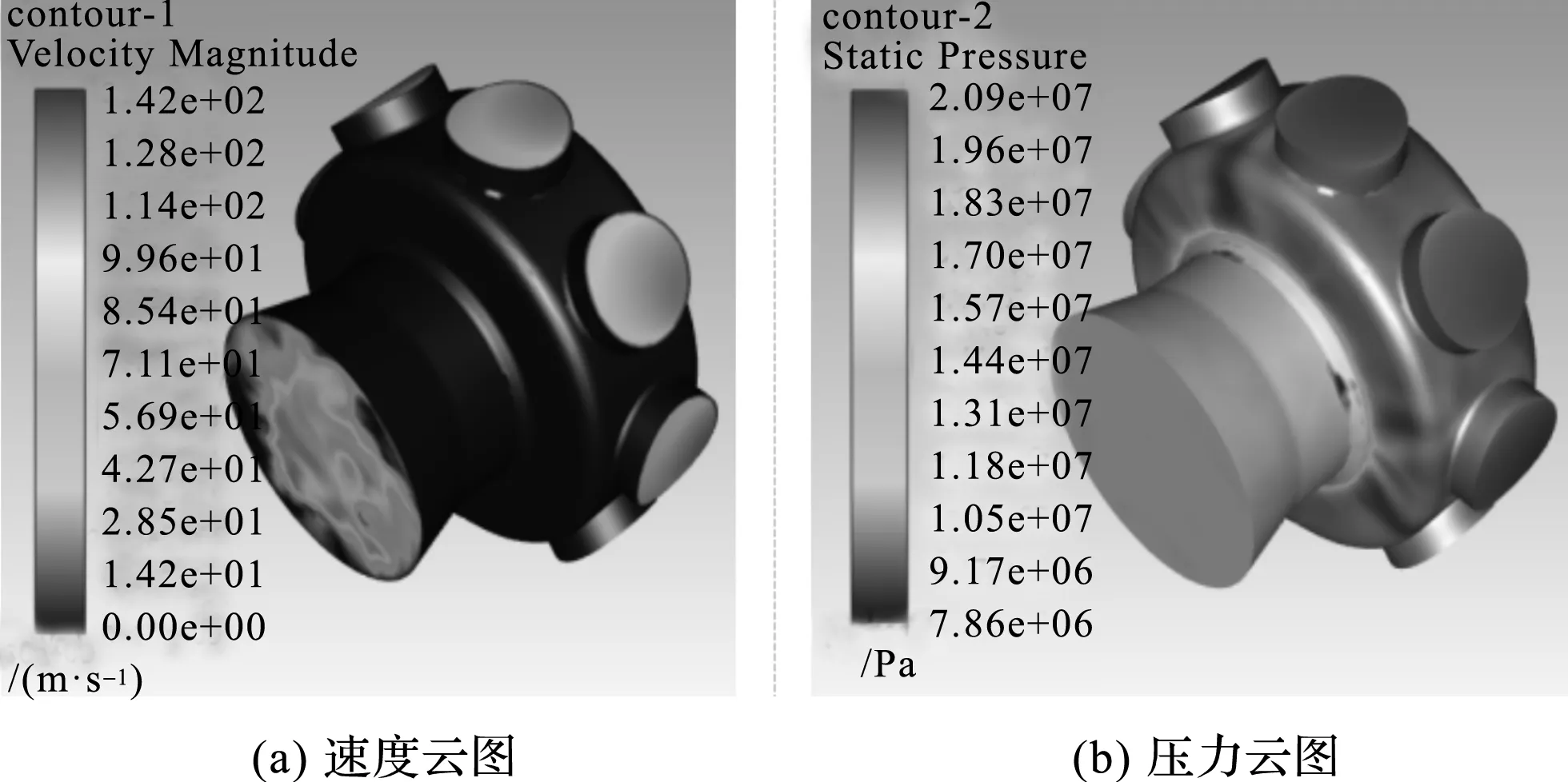
图19 三维云图(100%开度)

二维的速度和压力云图如图20所示。

图20 二维云图(100%开度)

笔者通过以上仿真分析得出了插装阀较准确的流场特性。

比较插装阀在不同开度时流场的速度云图与压力云图可知:随着阀芯开度逐渐增加,出口流量和出口压力逐渐增大,入口压力有所降低。

5 结束语

为了研究某液压打桩锤的组合插装阀动作过程中的响应特性和流场特性,笔者先介绍了某液压打桩锤专用组合插装阀的结构及工作原理,分析了插装阀阀芯运动的机理,并分别建立了插装阀开启和关闭两种状态的数学模型;然后,利用AMESim软件对插装阀控制腔压力、阀口流量、阀芯位移等进行了仿真分析;最后,利用Fluent仿真软件得到了插装阀在不同开度下的速度云图、压力云图。

主要过程及研究结论如下:

(1)利用AMESim软件仿真研究组合插装阀的响应特性,得到了组合插装阀在不同开度时的具体工况。在插装阀突然开启瞬间,插装阀入口压力为供油高压,出口压力为负载低压,插装阀两侧存在较大压差,阀口流量突然跃升,之后入口压力逐渐降低,流量稳定在一定值;

(2)利用Fluent仿真软件得到了主阀在不同阀口开度下的速度云图、压力云图等流场特性。通过压力云图可看出压力分布没有明显突变,阀芯开口设计较为合理,通过速度云图得到组合插装阀开度分别为20%、40%、60%、80%、100%时出口平均流速为19.64 m/s、39.20 m/s、53.22 m/s、55.44 m/s、57.28 m/s,可为平衡阀内部结构的设计和计算提供参考;

(3)随着开度的逐渐增大,流体最大流速依次减小,平均流量逐渐增大,入口处流体压力逐渐减小。

在今后的工作中,笔者将在考虑更多因素的情况下,对插装阀的工况进行模拟,通过提高流场计算精度,以此来获得更准确的结果。