基于改进组合Kriging模型的变速器噪声优化研究*
2022-12-26童林军林小娟蔡健文江兴洋
童林军,曾 威,林小娟,蔡健文,江兴洋
(1.佛山职业技术学院 汽车工程学院,广东 佛山 528137;2.西安石油大学 机械工程学院,陕西 西安 710065)
0 引 言
在变速箱运行过程中,会因齿轮振动产生噪声,这是其噪音的重要来源之一[1]。国内外学者对此已进行了许多研究。
欧健等人[2]运用多体动力学,建立了变速箱的动力学模型,对其进行了动力学分析,并运用声学边界元法预估了箱体辐射噪声,并通过试验对结果进行了验证,最后通过箱体结构优化达到了降噪的目的。刘春玲等人[3]建立了基于脉冲动量关系的变速箱拓扑变化模型,引入正交补码,研究了换挡拓扑变化引起的速度跳跃。ZHANG Q等人[4]根据变速箱的传动结构,建立了齿轮系统的动力学分析模型,以齿数、模数、压力角等宏观参数和齿廓角偏差、齿向角偏差、齿向鼓形量等微观参数为设计变量,建立了齿轮参数的优化设计模型,通过计算得到了优化的变速箱齿轮参数,降低了齿轮运行过程中的振动。彭显昌等人[5]基于壳体结构设计,建立了变速箱有限元模型,对壳体进行了刚度强度计算和约束模态计算,有效降低了壳体发生共振的风险。SON G等人[6]以箱体结构参数为设计变量,以噪声声压强度为优化目标,建立了变速箱箱体结构的优化设计模型,得到了变速箱箱体结构优化结果,达到了减少噪声辐射、降低变速箱降噪的目的。包英豪[7]根据齿轮啸叫产生的来源,建立了变速箱壳体的声学边界元模型,对变速箱进行了声学辐射仿真,得到了其噪声辐射云图和声压数值。蔡文奇[8]建立了两档变速箱传动系统Romax仿真模型,基于齿轮啸叫产生的原因,通过仿真的方式,得到了不同工况下齿轮的传递误差及轴承的动态响应特性。CAI W等人[9]采用控制齿轮振动优化方式,对其进行了模态分析、谐响应分析和声学响应分析,得到了不同设计参数对应的目标函数响应值,通过反复计算、寻优,得到了箱体最终的优化结构。
在寻优的过程中,变速箱齿轮系统的谐响应分析、模态分析和场点声学辐射计算等都需要耗费大量的时间,单次计算可能需要0.6 h以上[10]。而采用优化算法对优化模型进行寻优计算,可能需要反复计算上千次,这导致整个优化过程极为耗时,优化设计效率极低。
Kriging(KG)模型具有良好的非线性拟合能力,能够精确地拟合不同参数对应的齿轮动力学性能指标响应,尤其适合齿轮系统的非线性振动的动力学响应分析,可以显著降低目标函数的计算成本,达到提高变速箱优化设计效率的目的。
ZENG W等人[11]采用组合预测方法,提出了一种基于多个KG模型的并行自适应采样策略,该策略使用多个具有不同相关模型的KG模型,确定了采样过程中添加的新点,通过2个低维基准函数和1个高维基准函数,对该方法的有效性进行了验证。
在KG模型的建模方法方面,相关函数是影响该模型拟合精度的关键参数,且其中包含多种类型的标准模型。例如,高斯函数(Gassian)、指数函数(Exp)、三次函数(Cubic)、幂函数(Expg)、线性函数(Linear)、球函数(Spherical)和样条函数(Spline)等,建模前通常需要根据设计经验选择合适的相关函数,获得样本数据信息,然后建立KG模型,实现对目标函数响应的快速预测。但是,从组合预测理论角度来看,采用单一模型来获得样本数据信息,会造成最终建立的KG模型预测精度不高。因此,相关研究对其进行了改进。
曾威等人[12]采用组合预测方法,对KG模型进行了改进,建立了一种改进的组合KG模型,并将之应用到密封结构的优化设计中,取得了较好的效果。然而,该改进型模型在建模过程中,采用了全局固定的权重系数耦合方法,根据各个相关函数模型的全局精度分配一个固定权重,没有考虑各个相关函数模型的局部精度,导致最终建立的组合KG并非最优模型。
基于此,为提高变速箱的降噪优化效率,笔者引入KG模型,拟合不同设计参数下变速箱的动力学性能指标响应结果,并综合考虑各个单一相关函数模型全局精度和局部精度,对组合模型预测精度的联合影响,对组合KG模型进行改进,并建立一种基于改进组合KG模型的变速箱降噪方法,以提高变速箱噪声优化效率。
1 变速箱及噪声分析模型
笔者以一款两挡I-AMT变速箱为例。两档I-AMT变速箱结构如图1所示。

图1 两档I-AMT变速箱结构
根据影响变速箱噪声的相关分析,笔者以一档齿轮模数m1(mm),二档齿轮模数m2(mm),一档主/从动齿轮齿数分别为n1主和n1从,二档主/从动齿轮齿数分别为n2主和n2从,一档齿轮螺旋角β1(°),二档齿轮螺旋角β2(°),一档小齿轮齿形鼓形量C1-1B(μm),一档大齿轮齿形鼓形量C1-2B(μm),二档小齿轮齿形鼓形量C2-1B(μm)和二档大齿轮齿形鼓形量C2-2B(μm)作为设计变量。
其当前设计值如表1所示。

表1 变速箱设计变量及当前设计值
考虑因为制造、安装和弹性变形等造成一对相互啮合的齿轮出现传动误差。
为衡量不同设计参数下变速箱的传动误差,笔者建立变速箱传动误差计算方法(齿轮的水平、垂直方向如图1所示):
δ1=[(x1主-x1从)sinα1+(y1主-y1从)cosα1+(r1主θ1主+
r1从θ1从)]cosβ1+(z1主-z1从)·sinβ1-e1(t)
(1)
δ2=[(x2主-x2从)sinα2+(y2主-y2从)cosα2+(r2主θ2主+
r2从θ2从)]cosβ2-(z2主-z2从)·sinβ2-e2(t)
(2)
式中:δ1—第一档动态传动误差,μm;δ2—第二档的动态传动误差,μm;x1主—第一档主动齿轮水平位移,μm;x1从—第一档从动齿轮的水平位移,μm;x2主—第二档主动齿轮水平位移,μm;x2从—第二档从动齿轮的水平位移,μm;y1主—第一档主动齿轮垂直位移,μm;y1从—第一档从动齿轮的垂直位移,μm;y2主—第二档主动齿轮垂直位移,μm;y2从—第二档从动齿轮的垂直位移,μm;z1主—第一档主动齿轮轴向位移,μm;z1从—第一档从动齿轮的轴向位移,μm,z2主—第二档主动齿轮的轴向位移,μm;z2从—第二档从动齿轮的轴向位移,μm;θ1主—第一档主动齿轮转动角度,(°);θ1从—第一档从动齿轮的转动角度,(°);θ2主—第一档主动齿轮的转动角度,(°);θ2从—第一档从动齿轮的转动角度,(°);r1主—第一档主动齿轮的基圆半径,mm;r1从—第一档从动齿轮的基圆半径,mm;r2主—第一档主动齿轮的基圆半径,mm;r2从—第一档从动齿轮的基圆半径,mm;e1(t)—第一档的静态传递误差,μm;e2(t)—第二档的静态传递误差,μm。
为计算不同设计参数下变速箱的噪声等级,笔者建立的声学仿真模型如图2所示。

图2 变速箱声学边界元模型
笔者同时建立噪声辐射云图,如图3所示(分别为一档3 000 r/min,二档4 000 r/min)。
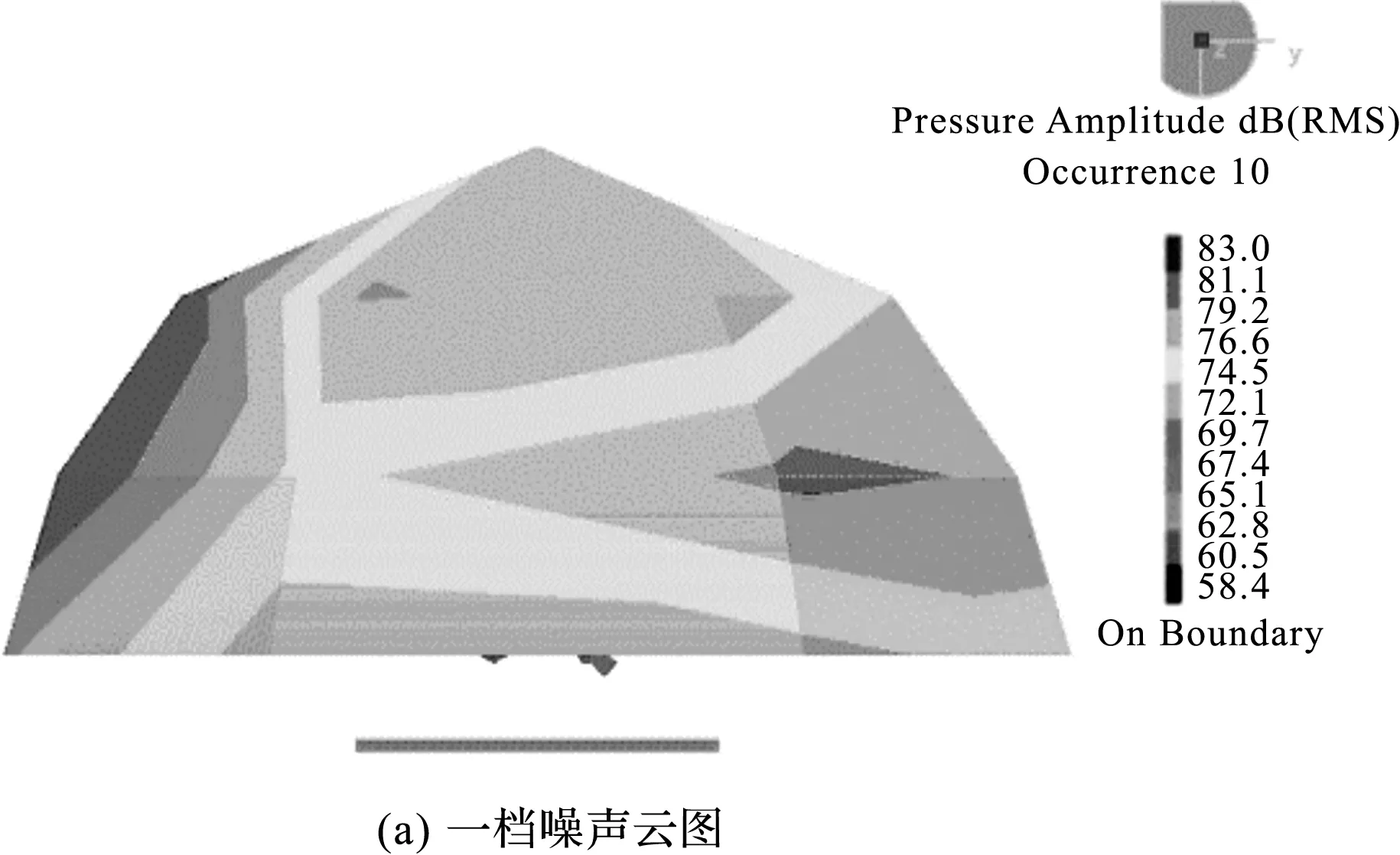

图3 变速箱原始设计噪声云图
利用该方法和模型,可以计算不同设计参数下变速箱的传动误差δi(μm)和振动噪声值d(dB)。
2 改进的组合KG模型建模方法
考虑到变速箱传动误差分析和振动噪声分析过程中,需要进行复杂的模态分析、谐响应分析或者声学响应分析,计算周期长,会导致变速箱噪声优化成本极高。
因此,笔者引入KG模型,拟合设计参数、传动误差值和振动噪声分贝值间的响应关系,以提高变速箱振动噪声优化效率。
2.1 普通KG模型
KG模型是一种估计方差最小的无偏估计模型[13],它能够精确地拟合强非线性样本数据间的相关关系,可以用来预测不同齿轮参数下变速箱的噪声等级指标。
普通KG模型包括回归部分与非参数两个部分:

(3)

其中:
(4)

Z(X)是均值为0,方差为σ2的随机过程,则任意两样本点间的相关关系可以描述为:
Cov[Z(xi),Z(xj)]=σ2R[R(xi,xj)]
(5)
式中:σ2—随机过程方差;R—n×n阶的对称正定对角矩阵;R(xi,xj)—任意两个样本点xi与xj的空间相关函数。
工程应用中,一般使用高斯相关函数对R(xi,xj)进行描述:
(6)
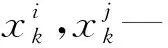

(7)
式中:r(x)T—长度为n的相关向量;f—长度为n的单位列向量。
其中:
(8)
为了获得模型的相关参数θk,使用式(6)所示的最大似然估计方法,即:
(9)
获得KG模型的相关参数θk之后,即可通过式(7)计算得到预测值,实现不同齿轮参数下变速箱的噪声指标值预测。
2.2 改进组合KG模型建模方法
根据普通KG模型的基本构成,相关函数R(xi,xj)是影响KG模型预测精度的重要参数,采用不同的相关函数,可以基于相同的样本数据,建立多种类型的KG模型,且不同类型的KG模型预测精度是不同的[14]。
为了提高KG模型预测精度,基于组合预测理论,相关研究人员将这些不同类型KG模型作为子模型,构建耦合多个子模型的组合KG模型,其基本方法如下:

(10)
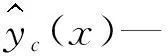
ωi的计算可以采用基于全局误差指标方法进行,即以最终构建的组合KG模型误差最小作为优化目标,以耦合系数ωi为优化设计变量,建立优化模型。
计算耦合系数值如下式所示:
(11)
式中:RMSE—组合KG模型的均方根误差,即其全局精度指标。
这种方法固然可以提高普通KG模型的拟合精度,但是当变量的取值范围较大时,在局部范围内可能存在局部精度(并非最优的情况),影响组合KG模型的预测精度,最终影响变速箱噪声指标的计算精度。
因此,笔者综合考虑全局和局部精度对KG模型预测精度的影响,建立一种既考虑全局误差,又考虑局部误差的组合KG模型。
改进组合KG模型的建模流程如图4所示。
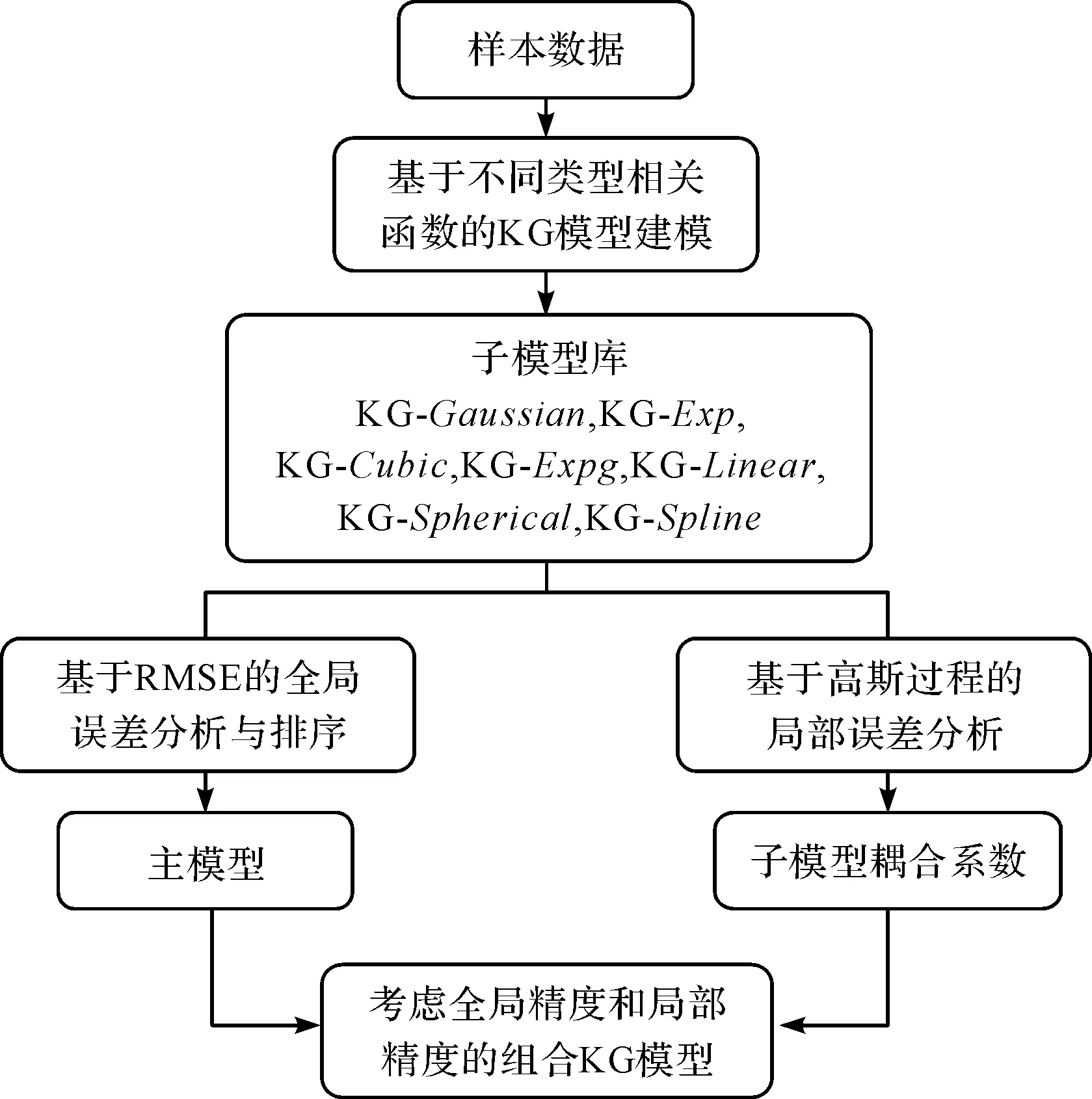
图4 改进组合KG模型建模流程
在MATLAB中,笔者采用DACE工具箱,分别基于不同相关函数(Gaussian、Exp、Cubic、Expg、Linear、Spherical和Spline)建立对应的KG模型,以作为子模型构建模型库,然后以均方根误差RMSE为误差评价指标,采用LOO交叉验证(Leave-one-out-cross-validation)方法对各个子模型进行全局误差评估,剔除低精度子模型,得到新的模型库;然后以新模型库中的最优全局模型为主模型,采用高斯随机过程方法计算模型库中子模型的局部误差。
其具体的计算方法[15]为:
f(x)~GP(m(x),c(x,x′))
(12)
通常可以将均值函数m(x)设置为0,而协方差则通过Bayes回归函数计算得到。
为了估计各子模型在变量域内任意一点的精度,笔者采用一种如式(12)所示的核函数,对子模型预测值的不确定性进行建模,用以表示子模型在设计域的精度:
(13)
式中:ym(xh)2—子模型在输入变量xh处的最佳预测值。
然后,笔者再根据式(13)所述过程计算耦合系数ωi:
(14)
笔者以之作为优化目标,采用式(8)进行计算,得到各子模型的耦合系数ωi,最终构建考虑全局误差和局部误差的组合KG模型。
3 变速箱噪声优化
3.1 设计变量与随机抽样
根据表1中变速箱的当前设计值,并考虑齿轮模数、齿数以及传动比等特殊要求,笔者确定了各设计变量的取值范围,如表2所示。

表2 变速箱各设计变量取值范围
在此基础上,笔者采用拉丁超立方抽样方法,在对应的取值范围中,分别对各个设计参数m1,m2,n1主,n1从,n2主,n2从,β1,β2,C1主B,C1从B,C2主B,C2从B进行抽样,得到k组样本点X(m1i,m2i,n1主i,n1从i,n2主i,n2从i,β1i,β2i,C1主Bi,C1从Bi,C2主Bi,C2从Bi)。
其中,i=1,2,…,k。
由于本模型中设计变量是12维,属于高维问题,其样本数为k=2p,p=h(h+1)/2,(其中:h—设计变量维度),因此,抽样样本数为156。
设计变量随机样本如表3所示。

表3 设计变量随机样本
3.2 变速箱传递误差与振动噪声组合KG模型
笔者选择变速箱传递误差δ1,δ2和振动噪声值d作为评价指标,采用建立的变速箱齿轮系统的传动误差计算模型和声学仿真模型,计算k组样本点对应的变速箱性能指标(δi,di),其中,i=1,2,…,j。
笔者以此为样本数据,根据改进的组合KG模型建模流程,对其中的子模型进行全局误差评估,得到的误差统计结果。
各子模型全局误差计算结果如表4所示。

表4 各子模型全局误差计算结果
笔者将误差阈值RMESm设置为0.2,剔除低精度KG模型,得到新的模型库。
更新后的子模型库如表5所示。

表5 更新后的子模型库
笔者以表5中筛选后得到的模型库中的最优全局模型为主模型,采用高斯随机过程方法计算模型库中子模型的局部误差,计算得到各子模型的耦合系数,如表6所示。

表6 各模型耦合系数值
笔者得到传递误差和振动噪声的改进混合KG模型S-δi和S-d,分别如下式所示:
(15)
(16)
(17)

3.3 基于改进组合KG模型的变速箱噪声优化
笔者以构建的传递误差和振动噪声的改进混合KG模型S-δi和S-di作为目标函数,以确定的各个设计参数m1,m2,n1主,n1从,n2主,n2从,β1,β2,C1主B,C1从B,C2主B,C2从B为设计变量,以齿轮根切、滑动率、干涉条件、齿顶厚和顶隙等作为多约束条件,建立变速箱的多目标优化设计模型,如下式所示:
(18)
式中:m—对应齿轮的模数。
笔者采用遗传算法,对建立的多目标优化设计模型进行寻优计算,找到各设计变量的最优设计参数Xopt=(m1iopt,m2iopt,n1主iopt,n1从iopt,n2主iopt,n2从iopt,β1iopt,β2iopt,C1主Biopt,C1从Biopt,C2主Biopt,C2从Biopt)=(1.5,1.5,18,64,29,53,20,20,3.03,7.06,5.18,2.03)。
为验证该方法的有效性,笔者将优化得到的齿轮结构参数代入建立的传动误差分析模型和声学仿真模型中,得到优化后变速箱的性能参数。
其中,噪声云图如图5所示。

图5 优化后变速箱噪声云图
并将之与优化前的性能参数进行对比,优化前后变速箱传动误差与噪声值对比如表7所示。
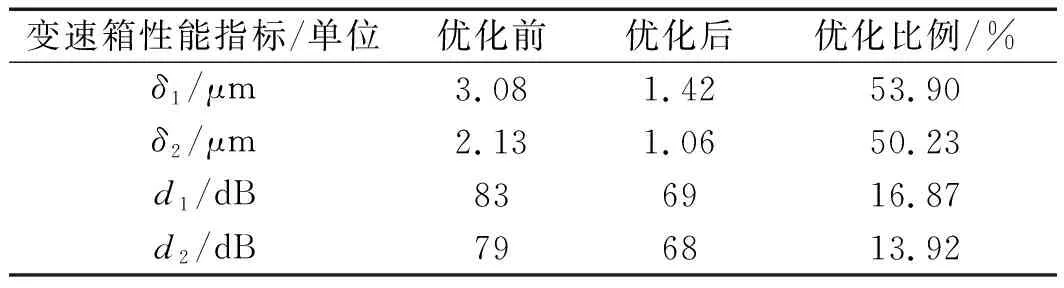
表7 优化前后变速箱传动误差与噪声值对比
从表7中分析结果可知:优化后一档传动误差和二档传动误差值分别降低53.9%和50.23%;一档和二档噪声分别降低16.87%和13.92%。
以上结果验证了笔者所提方法在保证变速箱传动精度、降低变速箱噪声方面的有效性。
进一步,为了验证该方法在降低变速箱降噪计算成本方面的有益效果,笔者还对优化计算成本进行了统计计算(两种方法均进行500次插值优化),并将其与传统的基于声学仿真方法进行了对比。
采用不同优化方法得到的优化结果与耗时对比,如表8所示。

表8 不同优化方法优化结果与耗时对比
根据表8中的优化计算结果可知:采用传统优化方法和笔者的优化方法得到的计算结果基本一致,这也验证了笔者所提出的方法的可靠性。
根据该表中的计算耗时相比,在使用笔者方法对变速箱进行降噪优化,计算耗时能够降低68.2%,优化效率得到显著提升。
4 结束语
针对齿轮振动分析极为耗时的问题,为降低因变速箱齿轮振动造成的运行噪声,笔者将KG模型引入变速箱噪声优化设计工作中,考虑相关函数对KG模型精度的影响,构建了一种组合KG模型,并在此基础上,开展了基于该组合KG模型的变速箱噪声优化研究。
主要研究结论如下:
(1)考虑齿轮设计参数对变速箱振动噪声的影响,建立了变速箱振动噪声分析边界元模型,完成了不同设计参数下变速箱振动噪声声压等级计算;
(2)考虑相关函数对KG模型精度的影响,考虑KG模型全局精度和局部精度的综合需求,基于组合预测理论,建立了一种改进的组合KG模型,并构建了基于该组合KG模型的变速箱振动噪声声压等级代理模型,实现了任意变量下,对变速箱噪声声压等级的快速计算;
(3)以传动误差和声压等级为优化目标,建立了基于组合KG模型的变速箱噪声优化模型,对变速箱齿轮参数进行了优化,并对优化结果进行了验证,结果表明,笔者所提方法不但能够降低变速箱噪声,而且能使变速箱噪声优化耗时降低68.2%。
后续的研究中,笔者将主要考虑相关函数对KG模型精度的影响,并基于上述改进的组合KG模型,实现任意变量下变速箱噪声声压等级的快速计算,同时,进一步提高其计算的精度。
