减速器齿轮轮辐设计及其噪声试验研究*
2022-12-26周迎春刘祥环袁仲谋
周迎春,胡 迪,刘祥环,袁仲谋
(株洲齿轮有限责任公司,湖南 株洲 412000)
0 引 言
随着相关行业对降低减速器噪声的要求不断提高[1-2],降低减速器噪声的难度也进一步加大,尤其是在电机转速越来越高的背景下,其难度更高。
在减速器中,从动齿轮轮辐的设计涉及噪声、强度、重量和成本,对减速器性能的影响很大。而只关注齿轮的微观修形,难以实现降低高速齿轮轴噪声的目标。因此,还需要进一步研究齿轮轮辐结构及零件的固有特性对高速齿轮噪声的影响。
HARRIS O等人[3]提出了一种通过分析不同齿轮轮辐对应的齿轮动态啮合力和传递误差,来进行噪声评价的方法,并对比分析了不同轮辐厚度的结果,以降低齿轮的噪声。GALE A等人[4]应用上述方法,设计并分析了齿轮轮辐带异形孔的结构,并以壳体声功率作为噪声评价对象进行了分析,分析发现,带异形孔结构的齿轮轮辐存在边频噪声,削弱了主频噪声的共振能量;但是这种降噪设计思路的实际降噪效果,还有待于实验来加以验证。葛海龙等人[5]采用MASTA对某变速器惰轮的轮辐进行了优化设计,并通过实验的方式得出了结论,即圆形通孔噪声低于腰形盲孔;但实验中变速器的转速不高,工况较少,将研究结果应用于减速器的齿轮轮辐设计,还有待于分析和进一步的验证。李春明等人[6]研究了轮辐的刚度与齿轮动载荷对变速器的影响,分析了不同转速和不同转矩的齿轮动力学响应,采用解析法和有限元法,证明了开孔的轮辐刚度小于实心轮辐刚度。李福援等人[7]提出了一种降低齿轮噪声的齿轮轮辐结构方案,该方案主要通过采用复杂结构或在轮辐中增加阻尼村料的方法;但这些方法容易降低产品的可靠性,并且增加额外成本。
以上几位学者所提出的轮辐结构容易在生产时产生动不平衡。关于动平衡对噪声的影响问题,以上学者也并未进行分析。同时,关于齿轮箱总成对齿轮轮辐固有模态的要求,以上学者也没有进行分析。
关于动平衡对噪声影响的研究,其主要方法是先建立其动力学分析模型,然后再对其进行分析。
LEE A S等人[8]基于有限元方法,通过施加关于动不平衡函数的外力,以此来考虑动平衡的影响,提出了一种计算齿轮耦合的转子系统的动不平衡响应方法,分析得到了某产品在第一阶扭转固有频率下,转子系统存在不平衡响应的共振情况。任朝晖等人[9]建立了偏心距影响的动力学解析模型,研究发现,偏心量增大,振动幅值相应增加,偏心量对扭转振动的影响大于对横向和轴向振动的影响。易园园等人[10]采用多体动力学软件,分析了齿轮几何偏心误差下的振动响应,得出了偏心误差产生的噪声调制特征,发现存在与偏心误差相关的边频带噪声。
但以上关于齿轮轴的动力学响应研究大多未考虑齿轮额外动不平衡量,因此,其对齿轮箱总成噪声的影响程度和范围不明确。同时,上述研究也未对齿轮啮合主阶次噪声的影响情况进行分析。
笔者设计固有模态满足系统频率要求的从动齿轮轮辐结构,并采用MASTA,对其进行噪声分析;基于不同转速下轮辐动不平衡量对减速器的影响,建立齿轮轴的动力学模型,分析动不平衡量激励的振动响应,并对其进行噪声对比测试,为减速器从动齿轮轮辐结构的设计提供相关经验。
1 轮辐结构与分析
1.1 轮辐结构设计
在减速器中,主动齿轮一般为轴结构,不存在轮幅;而二级从动齿轮与差速器联接,结构固定。故笔者主要研究对象为一级从动齿轮,以下简称“一从”。
一从装配在中间轴上,合称中间轴组件,结构如图1所示。
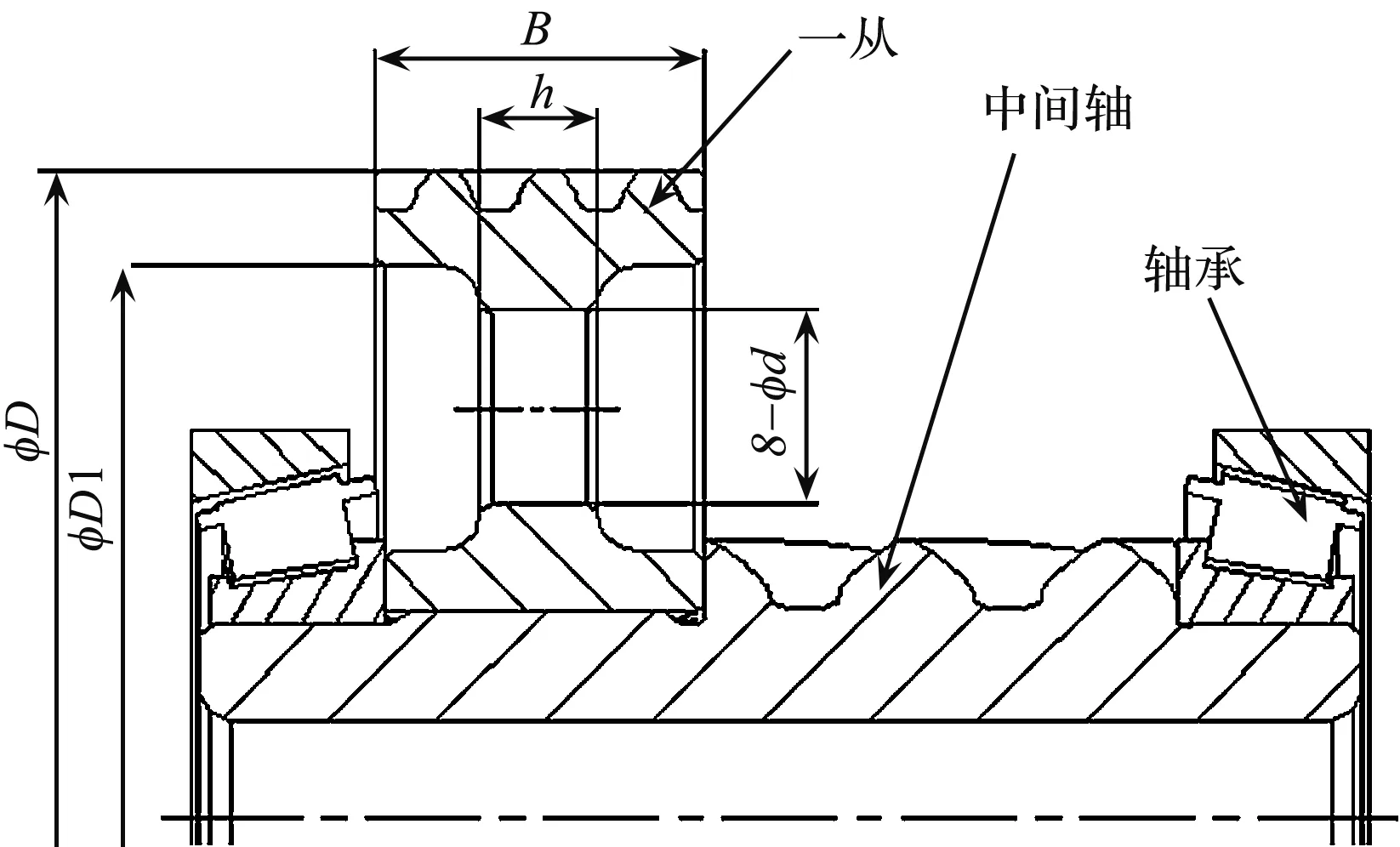
图1 中间轴组件图
图1中:一从与中间轴连接的方式一般采用花键过盈联接,或采用焊接的方式;轮辐厚度一般为齿宽的30%,大多采用打孔的方式,降低其重量。
为了验证不同轮辐结构对噪声的影响,笔者提出两种方案进行分析计算和测试。
其主要结构的参数如表1所示。

表1 主要结构参数
为了设计最优的齿轮轮辐,可以通过参数化研究,调整毛坯辐板厚的度或结构,以避免产生较大的齿轮啮合力。
经初步筛选,笔者确定采用方案二,采用异形结构和加强筋,在保证性能的同时尽可能不增加太多重量。
由于其最小边缘厚度会影响齿轮的强度,需根据全齿高满足ISO6336-3的要求,在这里不作为其优化设计的参数。
为了保证一级齿轮副啮合不激发一从本身的耦合模态,需要计算一从的使用频率范围,即:
f=nO/60
(1)
式中:f—频率,Hz;n—转速,这里取百公里时速的最高转速,r/min;O—一级齿轮阶次。
经计算可得到一从的最大使频率为5 000 Hz。因此,需要保证一从的固有模态尽可能地大于5 kHz。
笔者进行有限元分析后,得到两种方案的模态结果,如图2所示。

图2 一阶固有模态分析
由图2可知:方案一的一级模态为3.3 kHz,方案二的达到5 kHz,,满足了设计要求。
下面,笔者对两种方案在减速器总成中的噪声影响情况进行具体分析。
1.2 轮辐结构仿真分析
齿轮的轮辐越薄,则其重量越小,但会导致更高的齿轮啮合误差,尤其是在高负载的工况下。下面的分析均基于100%转矩。较薄的轮辐可能降低刚度,但也可能减少动态啮合力,因此,需要具体分析,结合传递误差结果来确定设计方案。
笔者将一从轮辐全有限元模型分别导入MASTA软件中,进行减速器总成的噪声分析[11],算得两种方案的动态啮合力如图3所示。

图3 一级齿轮动态啮合力
由图3可知:一级齿轮在啮合频率处的动态啮合力由方案一的2.5 kN/μm,降低至方案二的2.2 kN/μm。
分析得到两种方案的传递误差情况如图4所示。

图4 一级齿轮传递误差
由图4可知:一级齿轮的传递误差峰峰值由方案一的0.21 μm,降低至方案二的0.16 μm;方案二均有所降低。
由传递误差引起的振动激励壳体振动向外辐射噪声,分析而得的其壳体声功率对比情况如图5所示。
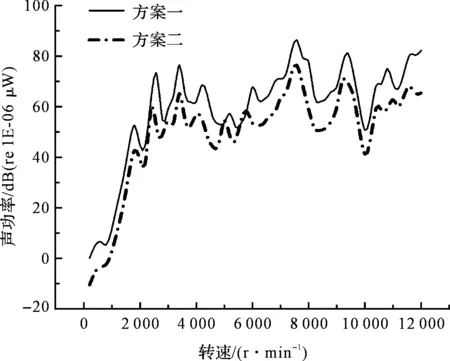
图5 壳体声功率对比
由图5可知:方案二的壳体声功率降低,噪声结果优于方案一。
2.1 两组临床效果比较 治疗2周后观察组临床效果优于对照组,且总有效率(94.64%)高于对照组(75.00%),差异有统计学意义(P<0.05)。见表2。
从以上分析结果可知:修改轮辐厚度和结构会改变传递误差激励、动态啮合力以及壳体声功率。因此,在进行设计优化时,需要对这些影响进行仔细平衡。
2 动平衡分析与影响
2.1 动平衡计算
当一从轮辐采用加强筋等非圆周的异形结构时,毛坯不能车削加工,需采用锻造的方式,以保证其几何结构。
由于制造的误差和实物的不对称等因素,会产生额外的动不平衡质量,导致轴在旋转时会产生离心惯性力,进而影响其降噪的效果。
此处,笔者以某减速器一从为例。
在半径为45 mm时,动不平衡量可分布在0.4 g~9.3 g之间。由于电机的转速最高达到18 000 r/min,一从的转速最高可达5 000 r/min,有必要分析动不衡量作为额外激励产生的减速箱响应,以确定其许用残余动平衡量。
动不平衡质量随转速大小产生的离心惯性力计算公式为:
F=mr(2πn/60)210-9
(2)
式中:F—离心惯性力,kN;n—从转速,r/min;r—半径,mm;m—动不平衡质量,g。

图6 动不平衡惯性力图
由于在离心惯性力作用下,减速箱总成各处刚度情况不同,将产生周期性的振动。
为了分析在这个周期离心惯性力的激励下系统响应,需建立齿轮轴振动系统动力学模型。
笔者将中间轴组件等效为转子轴(忽略一从齿轮搅油的阻尼,不考虑陀螺效应,不考虑重力),设e为一从的动不平衡偏心量,θ1、θ2、θd分别为主动齿轮、从动齿轮、输入轴的扭转振动角,建立坐标系O1、O2及一从质心坐标为G。
齿轮轴动力学模型如图7所示。
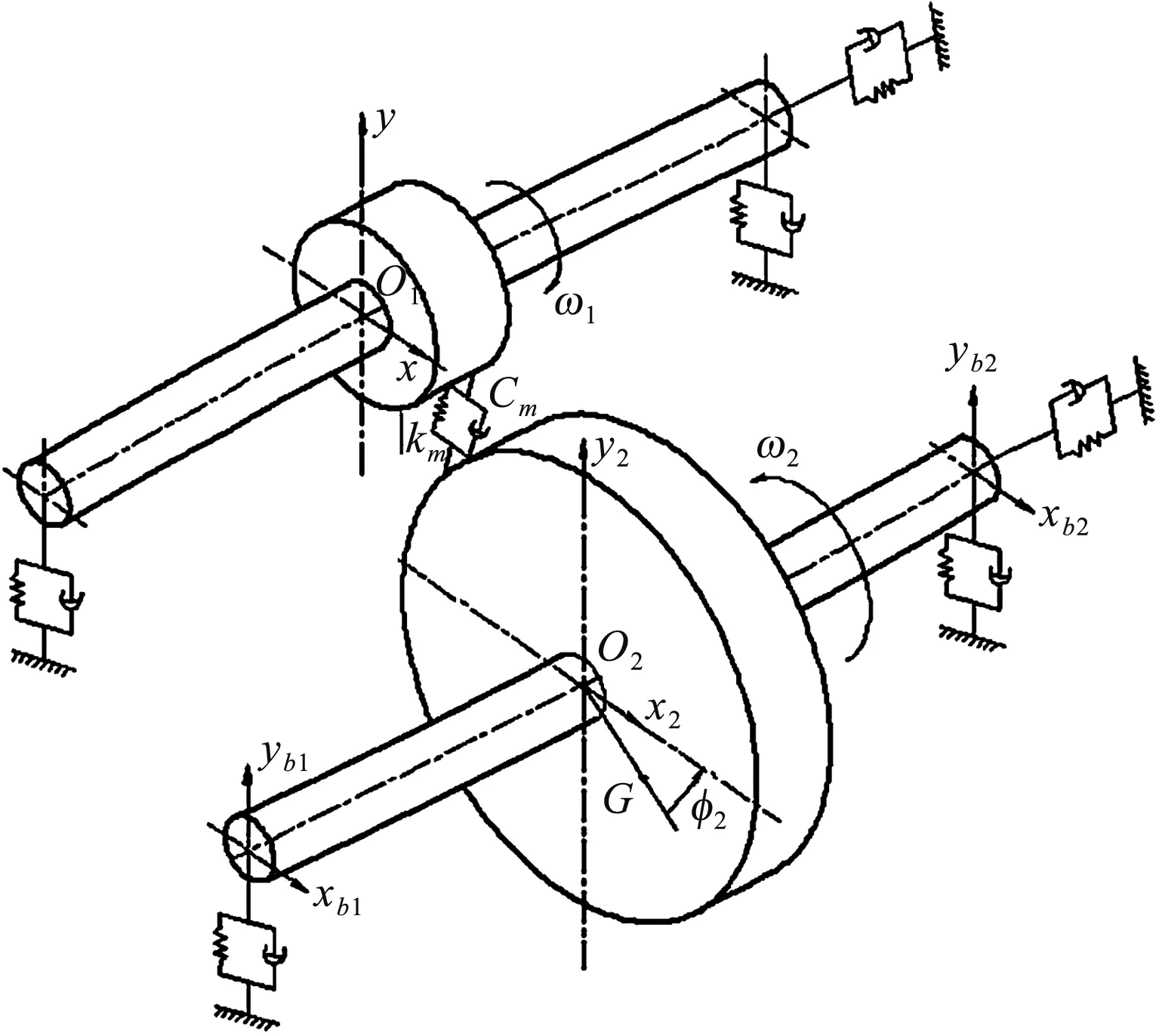
图7 齿轮轴动力学模型
根据图7模型,采用集中质量参数法可得动力学方程如下[12,13]:
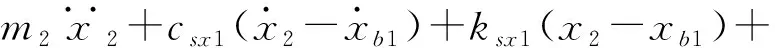
(3)

(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
式中:csx1,csy1—输入轴阻尼,N/(m·s-1);csx2,csy2—中间轴阻尼,N/(m·s-1);ksx1,ksy1—输入轴弯曲刚度,N/m;ksx2,ksy2—中间轴弯曲刚度,N/m;kt1—输入轴扭转刚度,Nm/rad;kt2—中间轴扭转刚度,Nm/rad;Fb1x,Fb1y—中间轴左轴承受力,N;Fb2x,Fb2y—中间轴右轴承受力,N;T1—输入转矩,Nm。
2.2 振动分析
笔者将输入转矩、质量及齿轮参数进行赋值计算,由MASTA软件计算得到轴承刚度及齿轮时变啮合刚度,并将其代入计算公式,进行初步的振动响应计算[14,15]。
此处以xb1的振动加速度为例进行分析。激励的对比情况如图8所示。
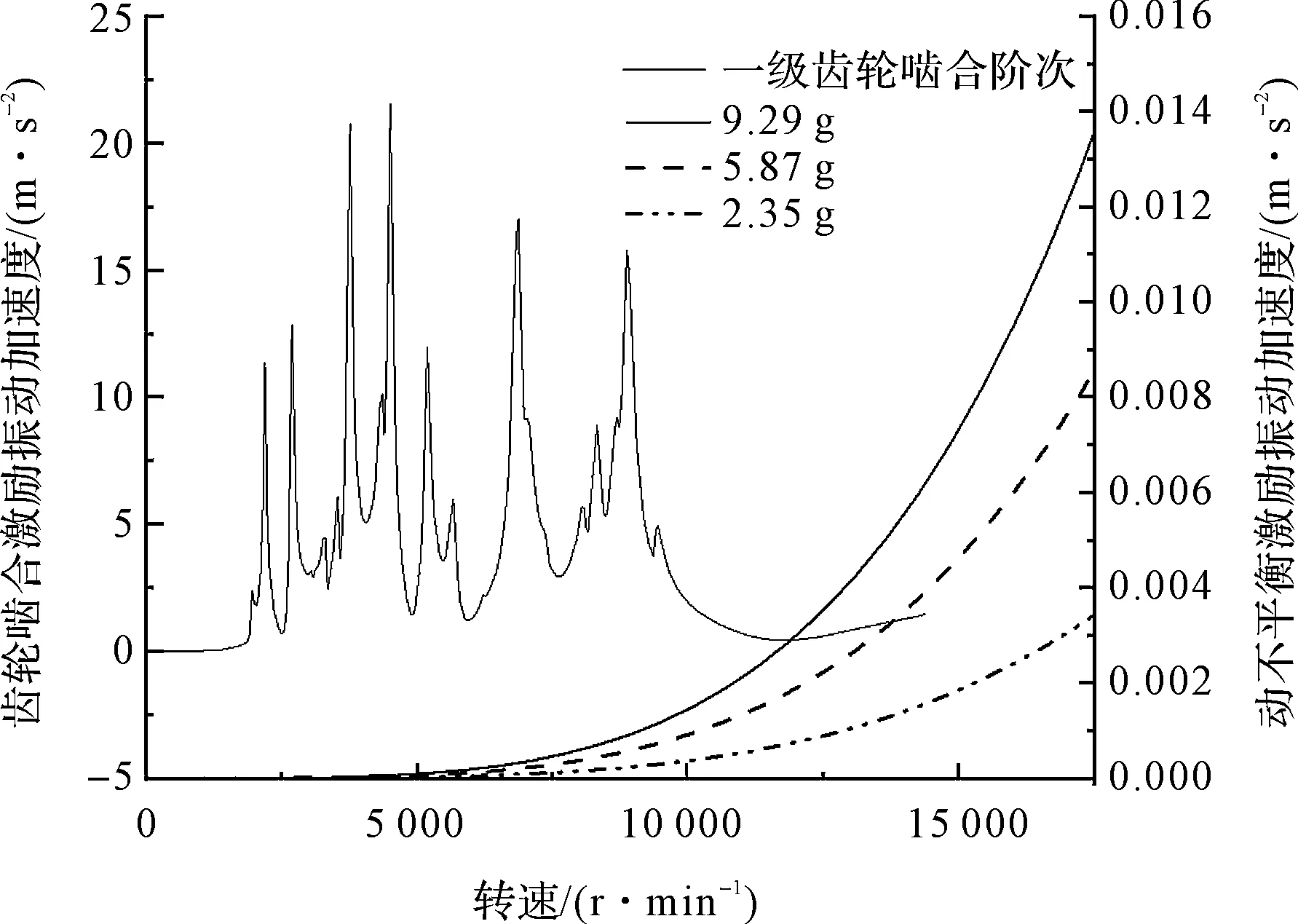
图8 激励对比
由图8可见:动不平衡量的激励随转速升高而增加,随动不平衡量增大而增加,但在工作转速范围内;相对齿轮的激励小。
为了确定一从在转速范围内的振动耦合情况,笔者计算得到系统耦合模态,其中,一从的模态第一阶为819.8 Hz,第二阶为856.5 Hz。
模态振型如图9所示。

图9 一从一阶模态
由图9可知:一从振动为Z向摆动,与动不平衡量激励力方向不同,无共振风险。
一从的旋转阶次为0.28阶,其二倍阶次为0.56阶,一级齿轮的啮合阶次为25阶,耦合情况如图10所示。

图10 坎贝尔图
由图10可知:一从的旋转阶次与中间轴组件相同,与系统的一阶耦合模态在工作转速范围内没有相交,所以一从由动不平衡激发的周期旋转惯性力没有产生共振,没有因共振导致的振动加剧的情况。
3 试验验证
为了验证轮辐方案一和方案二的差异,笔者采用同一台样本变速箱,仅更换两方案的中间轴组件,对其进行对比测试。
测试在半消声室台架进行。被测样机由驱动电机实现调速,输出由负载电机进行扭矩控制。
近场布置麦克风采集变速箱的噪声数据。
台架测试图如图11所示。

图11 台架测试
笔者采用数据分析软件,对近场噪声进行阶次分析,得到了不同方案的一从的齿轮啮合阶次噪声。
不同轮辐结构噪声测试结果对比如图12所示。

图12 不同轮辐结构噪声测试结果
由图12测试结果可知:方案二的异形结构的一从,在电机转速8 000 r/min以后,一级阶次噪声明显优于方案一(约5 dB以上),且整体噪声曲线更平滑。
由于中间轴组件装配后不便检测动平衡,针对动不平衡量对减速器噪声的影响,笔者采用多样本统计分析法来对此进行验证。根据动不平衡量的范围,笔者将其分成A、B两组,其中,A组动不平衡量均在1.5 g以内,B组在2.9 g~9.3 g之间。
通过装机进行测试,其结果如图13所示。

图13 不同动不平衡量的齿轮阶次噪声
图13中:粗线为A组(动不平衡量小),细线为B组(动不平衡量大),动不平衡量具体数值如图例。
由测试结果可知:A组和B组两组样本的噪声曲线均落在A组的2倍标准差(图中浅色带)内;在全转速段内,包括高速段,噪声值并未随动不平衡量呈线性相关性。
为了确定两组数据是否具有显著性差异,笔者采用双样本检验统计法[16],假设两组样本存在显著性差异,计算假设检验统计的概率P值(Probability value)。
各转速统计P值分析结果如图14所示。

图14 各转速统计P值分析
由图14可知:全转速范围内的P值均大于0.05,拒绝两组样本存在显著性差异的假设,说明A组、B组样本的噪声值与被测动平衡量数值大小无显著差异。
综合以上分析可知:对于笔者所研究的减速器总成,动不平衡量范围在9.29 g以内时,对减速箱噪声没有明显的影响。
4 结束语
为了满足减速器苛刻的噪声要求,笔者对其齿轮轮辐的设计进行了分析研究,运用MASTA软件对齿轮轮辐结构进行了优化设计,实现了减速器降噪的目的,并针对异形结构齿轮轮辐带来的动不平衡的影响,对其进行了相应的分析和测试验证。
研究结论如下:
(1)在噪声效果上,方案二齿轮轮辐的异形结构优于方案一的传统结构。实测电机转速在8 000 r/min以上时,噪声比传统结构低5 dB以上;
(2)方案二异形结构齿轮轮辐的动不平衡量在9.29 g以内时,动不平衡的振动激励小于齿轮激励。统计噪声测试结果,P值大于0.05,说明在9.29 g范围内的动不平衡量对研究对象减速箱噪声无明显影响。
虽然采用异形结构的轮幅可以提升降噪水平,但也增加了其自身的重量。因此,在后续的研究中,笔者将重点进行轮幅结构轻量化设计的相关分析和研究。
