先导活塞式泄压阀的运动规律
2019-11-11杨开林
杨开林
(流域水循环模拟与调控国家重点实验室 中国水利水电科学研究院,北京 100038)
1 研究背景
泄压阀或泄放阀和减压阀是一种预防水击危害的安全阀,当管道水击发生时,一旦水压超过设计临界值,则阀门迅速开启泄水减压,防止水压的进一步升高,稍后,当水压低于设计临界值时,则阀门缓慢关闭。
泄压阀可分为自立式和他立式。自立式泄压阀是一种不用油压控制和电动控制的防水击破坏的阀门,阀门的启闭完全受输水干管水压控制,特点是:阀门开度随时间的变化在水击过程中是未知量,包括阀门是否会完全开启。他立式泄压阀是需要外力操控的阀门,例如水电站和泵站采用的全油压或者电动控制的调压阀等,一旦发生水击,阀门按照事先规定的开度和时间的关系启闭,不受输水干管水压变化的影响。
先导式泄压阀属于自立式泄压阀,主要划分为两种类型:隔膜式和活塞式。先导隔膜式泄压阀受隔膜材料限制,适用水压范围是小于1.6 MPa;先导活塞式泄压阀适用水压范围基本上不受限制。
泄压阀的发展历史悠久,已经有很多相关的理论研究成果。早期的泄压阀为弹簧式,阀瓣与阀座的密封靠弹簧的作用力,当水压超过设定值时,泄压阀克服弹簧力瞬时开启放水泄压,一旦水压小于设定值时,泄压阀在弹簧作用下瞬时关闭。Singh[1]和Krivosheev[2]建立了弹簧式泄压阀的二阶运动方程,以阀进口压力作为激励,分析了泄压阀在工作过程中的稳定性。贾不假和胡松柏[3]定性分析了弹簧式泄压阀的动作特性。郭崇志和朱寿林[4]采用数值模拟的方法分析了弹簧式泄压阀开启的瞬态动力学问题,包括瞬态流场的变化,以及相关瞬态参数在典型路径上的变化与瞬态开启过程的关系。由于弹簧式泄压阀存在运行稳定性问题,且它的瞬时全关可能产生危险的闭阀水锤,目前正在被先导式泄压阀代替。张月蓉等[5]通过对大流量泄压阀建立关于压力和开度的数值试验模型,然后利用多元非线性回归的方法建立了压力和开度的经验模型。朱万春等[6]针对长输油管道广泛应用的泄压阀,应用CFD方法对其内部流场进行了分析计算,指出泄压阀的阻力系数与开度、管径有关,开启压力对泄压阀的阻力系数几乎没有影响。单如健等[7]运用Fluent动网格和UDF技术对某泄压阀管道模型进行数值模拟,结果表明:泄压阀阀芯部分会有明显的节流效应,导致阀内速度的突变;随着管道内压力的增加,管道内部速度总体呈现增大趋势,噪声和速度具有一定的相关性。
目前,在输油管道中已经普遍推广使用先导活塞式泄压阀,它由导阀和主阀组成,通过导阀的启闭来控制主阀的启闭,主阀具有快开慢关的功能,能够迅速开启防止水压的大幅升高,而缓慢关闭可防止自身关阀产生的水击危害。导阀感应水压的变化,反应灵敏,动作迅速,在设定压力的1%的范围内就能够动作,主阀响应时间小于0.1s(房旭鹏[8];张兴等[9])。梁建军等[10]应用商业软件PIPE2008计算分析了先导式泄压阀对输水工程的水击防护效果,成果在工程中得到应用。
由于先导活塞式泄压阀具有动作灵敏、安全可靠性高、投资小的特点,随着我国输水工程建设的不断发展,它必将会在输水工程的水击危害防护方面发挥越来越重要的作用,但是,目前对这种阀的理论研究尚不成熟,缺乏对其运动规律与结构参数和水力学参数关系的数学描述,使得在应用的过程中存在下述主要问题:
(1)选用时缺乏对影响主阀启闭运动相关因素的了解,包括水压、弹簧、重力、摩阻力等是如何影响主阀的运动的;
(2)厂家无法提供确切的主阀启闭规律,主阀的开启、关闭时间无法事先设定,只能通过现场调试,由于受事先泄压阀配置的影响,现场调试结果可能与设计预期存在较大差异,达不到水击控制的要求。
因此,系统深入研究先导活塞式泄压阀的主阀的运动规律具有重要的理论和实用意义。本文的主要目的是,基于结构运动力学和水力学原理,首先建立主阀的运动方程,确定各影响因素相互之间的函数关系;然后,根据主阀关闭和开启的水力学特点,重点研究关键结构参数对主阀启闭运动规律的影响,并对主阀关闭过程进行理论解析;最后,通过数值试验研究关键参数对主阀开启和关闭的影响。
2 先导活塞式泄压阀特点及工作原理
图1示出了目前的一种典型先导活塞式泄压阀,它是一种导阀控制、液压驱动的控制阀,主要由主阀、导阀、针阀和滤网等组成。主阀一般为截止阀,例如直流式、角式、柱塞式截止阀等。活塞与主阀瓣由阀杆刚性连接,在活塞上腔和下腔压力差作用下可以在活塞缸内往复运动。活塞上腔水压受导阀控制,下腔通过缓冲孔与阀体内压力相通,可使主阀的关闭得到缓冲。导阀也是一种泄压阀,它由止回阀,控制腔、弹簧等组成,其止回阀的启闭受控制腔水压和弹簧的控制。当水压小于1.6 MPa时,导阀密封可采用隔膜式,如图1所示,但是,当水压大于1.6 MPa时,导阀一般采用活塞式。针阀是一种微调阀,主要用作调节流进隔膜上腔的流量大小,以控制主阀的启闭速度。滤网的功能是过滤存在于管道介质中的颗粒物质,以防止进水管和上腔的堵塞。取样管两端分别与导阀和主阀连通,使得导阀控制腔水压几乎完全等于主阀进口水压或者输水干管水压。进水管进口与主阀进口相通,而出口分别与上腔管和泄水管相通。上腔管一端与上腔相通,另一端与进水管和泄水管交汇。
液压传动系统的作用是对泄压阀主阀的启闭实施自立式自动控制,主要部件是:
(1)控制调节装置,包括导阀(控制阀)、针阀(调节阀)和缓冲孔等,用来控制液压系统的压力、流量和流动方向,以保证执行元件完成预期的动作;
(2)执行元件,包括活塞、阀杆、上腔和下腔等,用以将输水干管液体的压力能转换为主阀瓣上下运动的机械能;
(3)辅助装置,进水管、上腔管、泄水管、缓冲孔与各种管接头、滤网、检修阀和压力计等,它们起着连接、传递压力、输送流量、过滤、测量液压和检修等辅助作用,以保证液压系统可靠.稳定、持久地工作。
活塞式泄压阀的工作原理是:当输水管道发生水击时,一旦主阀进口压头Hp超过导阀开启的临界压头Hcri,即Hp>Hcri,则导阀弹簧受导阀控制腔水压(主阀进口水压或者输水干管水压)作用压缩,导阀止回阀向上运动瞬时全开,致使上腔水压迅速降低,这时主阀瓣(主阀阀瓣)在进口水压的作用下迅速向上运动,主阀开启,迫使上腔水体通过上腔管与进水管来流汇合后一起通过导阀止回阀-泄水管迅速排出,同时,随着主阀的开启,输水干管水体通过主阀孔口被泄放到外界,以避免干管水压超过设计限制。当Hp<Hcri时,导阀弹簧伸展复位,导阀止回阀向下运动瞬时全关,然后,主阀进口液体通过进水管-上腔管流入上腔,使上腔水压迅速增加,迫使主阀瓣在活塞面水压+弹簧力+重力的作用下向下缓慢运动,直到完全关闭。
若在主阀关闭过程中Hp>Hcri,则导阀重新开启,使主阀停止关闭,重新增大主阀开度,防止干管压力持续升高。换句话说,在主阀开启泄水减压的过程中,导阀可能经历多次全开和全关的过程。
3 主阀的运动方程
为了突出主要因素的影响,假设:
(1)泄压阀上腔进水管、上腔管、取样管、泄水管很短,水流的惯性力和弹性可忽略不计;
(2)泄压阀的水道高程差与干管水压相比微小,可忽略不计;
(3)阀杆截面积与活塞或主阀瓣面积相比小得多,在计算活塞或主阀瓣上下面水压差时可忽略不计。
当以图1主阀运动部件作为控制体,并以主阀(阀瓣)开启方向为行程Y的正向,则作用在控制体上的力是活塞与主阀瓣上下表面的水压力、运动部件的重力、主阀弹簧力、活塞环和阀杆表面摩阻力,其中:水压力与作用表面垂直,重力和弹簧力方向与Y方向相反,摩阻力与运动方向相反。在此条件下,主阀运动部件的运动方程为:
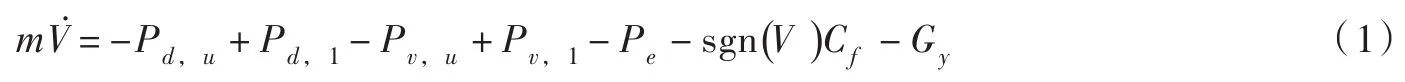
式中:m为主阀运动部件的质量,kg;V=dYdt为运动速度,m/s;;Y为主阀行程,m;Pd,u、Pd,1为活塞上、下面的水压力,N;Pv,u、Pv,1为主阀瓣上、下面的水压力,N;Pe为主阀弹簧力,N;Cf为活塞环(密封圈)和阀杆表面摩阻力,N,其中sgn(V)为符号函数。当主阀开启时,sgn(V)>0,取值为1;当主阀关闭时,sgn(V)<0,取值为-1;Gy=Gsinα为运动部件沿Y方向的重力,N;G为运动部件(活塞、主阀瓣、阀杆)的重力,N;α为阀杆(Y方向)与水平面的夹角。
根据胡克定律,弹簧力与行程的关系为
一般情况下,普通硅酸盐水泥或者是硅酸盐水泥是道路桥梁施工中常用的施工材料,但是,为了能够切实提高整体建设项目的质量,就可以考虑适用钢纤维混凝土材料。主要是钢纤维混凝土在施工过程中,其厚度摊铺量可以比较小,同时它具备抗压、抗磨抗冻等特点,因此,水泥的选择上可以采取钢纤维混凝土进行施工。

式中:k为弹簧系数,N/m。弹簧系数的选择主要考虑主阀关闭的要求。
如图1所示,阀杆和密封填料之间密封要求不高,密封填料主要为阀杆的上下移动起稳定导向作用,渗漏对主阀运动的影响不大,在一般情况下阀杆表面摩阻力可忽略不计,但是,活塞环的密封要求较高,所以活塞环的摩阻力较大,必须考虑。活塞环摩阻力的理论计算公式(陆培文)[11-12]是

式中:Z1为活塞环数;fm为摩擦系数,初步计算可取0.2;Dd活塞直径,m;h为活塞环径向厚度,m;b为活塞环的宽度,m;Δ=S-δ为活塞环自由状态与工作状态间隙之差,m;s为活塞环自由状态开口间隙,m;δ为活塞环工作状态开口间隙,m,是防止工作温度下活塞环与气缸热膨胀卡紧而预留的间隙,一般为0.25×10-3~0.5×10-3;E为活塞环弹性模量,Pa。对矩形截面铸铁活塞环:当Dd≥0.05 m时,h=(1/22~1/36)Dd,大直径活塞取下限;b=(0.4~1.4)h,较大直径活塞取较小值;活塞环自由开口间隙s=(3~4)h。
根据假设(1)和(2),当主阀关闭时,水体由进水管和上腔管流入上腔,由伯努利方程可得活塞上面的水压是:

当主阀开启时,上腔水体由上腔管流出与进水管水流在图1点A合流后通过泄水管排出:

式中:Hd,u为上腔的压头,m;Hv,1为进水管进口或者主阀瓣下面的压头,m;Qp为进水管流量,m3/s;Qu为上腔管流量,m3/s;为管道的阻抗系数;f为沿程阻力系数;L为管长,m;d为管径,m;ζ为管道局部阻力系数;A为管道过水截面积,m2;g=9.8 m/s2,重力加速度;Sp为进水管的阻抗系数,可通过针阀开度调整;Su为上腔管的阻抗系数,由于上腔管流动方向发生变化,其局部阻力系数因流动方向的不同而不同。
当主阀关闭时,活塞上面水压力是:
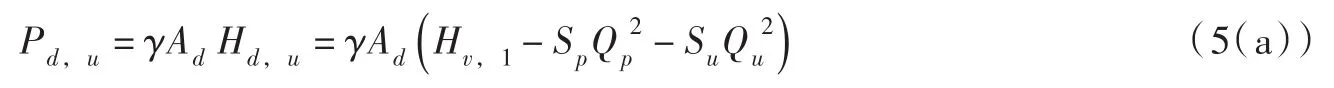
当主阀开启时:

式中:γ=gρ为水的比重,N/m3;ρ为水的密度,g/m3;Ad为活塞面积,m2。
缓冲孔也具有双向流动特性,当主阀关闭时,液体从下腔流出,活塞下腔水压与缓冲孔出口水压(主阀瓣上面的水压)的关系为:

当主阀开启时,液体流入下腔:

式中:Hd,1为下腔的压头,m;Hv,u为主阀瓣上面的压头,m;Q为缓冲孔的流量,m3/s;为缓冲孔的阻抗系数,ζori为缓冲孔局部阻力系数,nori为缓冲孔数,Aori为缓冲孔面积,m2。考虑到主阀瓣上面的压头分部的不均匀性,缓冲孔可以是多个小孔的组合,将它们轴对称布置在下腔底部。
主阀瓣下面和上面的水压力差:

式中Av为主阀瓣面积,m2。
把式(2)、(3)、(5(a))、(7)代入式(1)得主阀关闭的运动方程:

把式(2)、(3)、(5(b))、(7)代入式(1)得主阀开启的运动方程:
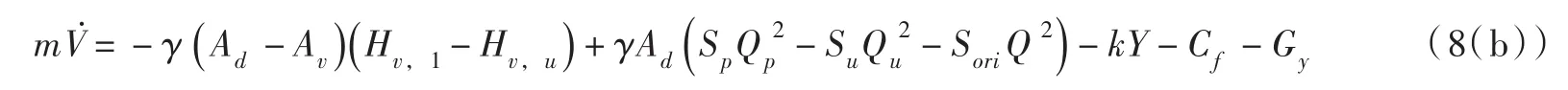
下面将根据主阀关闭和开启过程的水力学特点,建立液压传动系统流量Qp、Qu、Qs、Q与主阀运动速度V的函数关系。
3.1 主阀关闭速度与液压传动系统流量的关系当导阀瞬时关闭后,泄水管流量Qs=0,主阀进口液体通过进水管和上腔管流入上腔,主阀开始关闭,Q≤0,水从缓冲孔流出。由图1点A流动的连续性可得:

式中负号表示实际流动与图1参考方向相反。
当主阀关闭时,活塞向下运动,上腔体积增加的改变量与流入、流出流量的关系是:
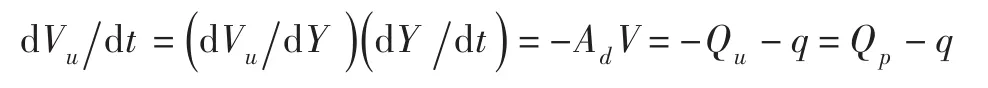
即:

式中:Vu为上腔体积,m3;q为活塞环的渗漏流量,m3/s。
活塞下腔体积减小的改变与流入、流出流量的关系是:
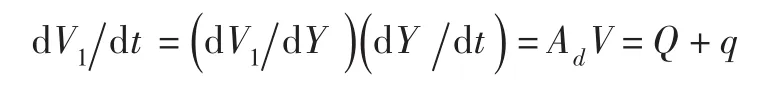
即:

式中V1为下腔体积,m3。
活塞渗漏流量与水头损失的关系可描述为:

式中:Gd为活塞渗漏流量系数;A1=πDdδ,δ为缸套与活塞环之间的间隙,m,在一般情况下,δ=3×10-5m[11-12]。
当式4(a)-式6(a)时,则:
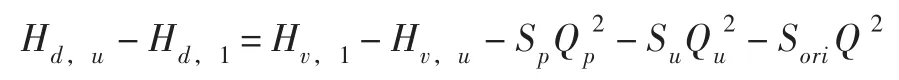
把式(9)、式(10)、式(11)代入上式得:
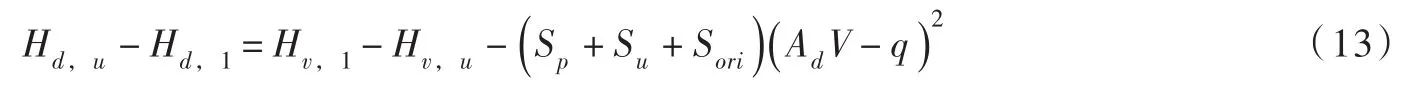
把式(13)代入式(12)得:
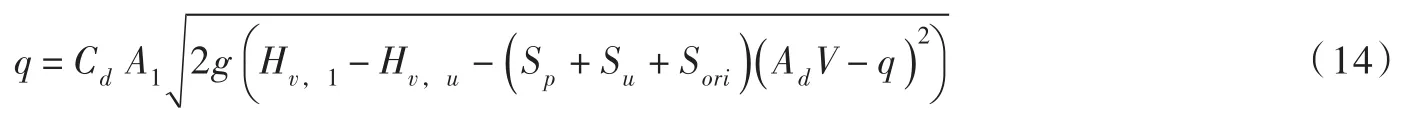
当已知(AdV-q)时,可由上式计算活塞渗漏流量。
把式(9)、式(10)、式(11)代入式(8(a))得主阀关闭的运动方程:
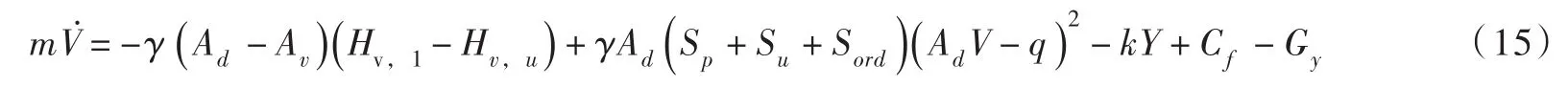
显然,主阀的关闭速度不仅与惯性力、弹簧力、摩阻力、重力有关,与活塞和主阀瓣面积有关,而且与水压、渗漏流量及进水管、上腔管和缓冲孔的阻抗系数有关。
3.2 主阀开启速度与液压传动系统流量的关系当导阀瞬时开启后,在主阀瓣水压力的作用下,主阀瓣开始向上运动开启,V>0,进水管和上腔管流量在A点汇流后通过泄水管排出,主阀瓣上液体通过缓冲孔流入下腔。图1交汇点A处连续性方程是:

根据假设(1)和(2),列出进水管进口与导阀泄水管出口之间的伯努利方程可得:

式中:Hs为泄水管出口压头,m;Ss为泄水管的阻抗系数。在一般情况下,Hs接近大气压头,Hs≈0,可忽略不计,这样,把式(16)代入式(17)消去Qs得:
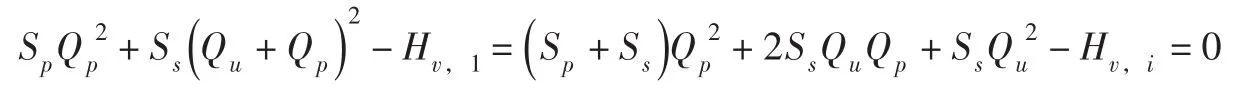
求解得:
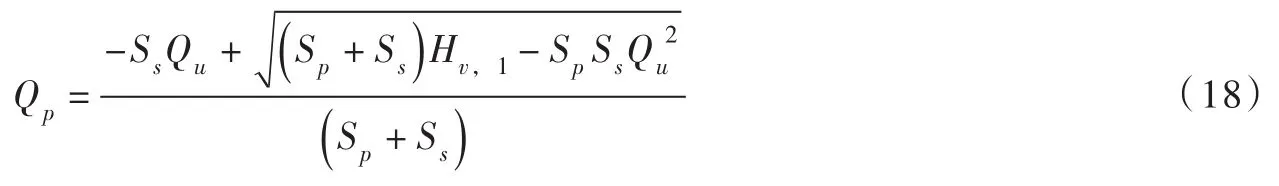
当导阀开启时,活塞上下腔水压差较小,活塞的渗漏可忽略不计,这时,

将式(18)和(19)代入式(8b)得主阀开启的运动方程:
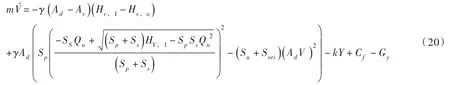
显然,主阀的开启速度不仅与惯性力、弹簧力、摩阻力、重力有关,与活塞和主阀瓣面积有关,而且与水压、进水管、上腔管、泄水管和缓冲孔的阻抗系数有关。
式(20)的数值计算差分方程是:
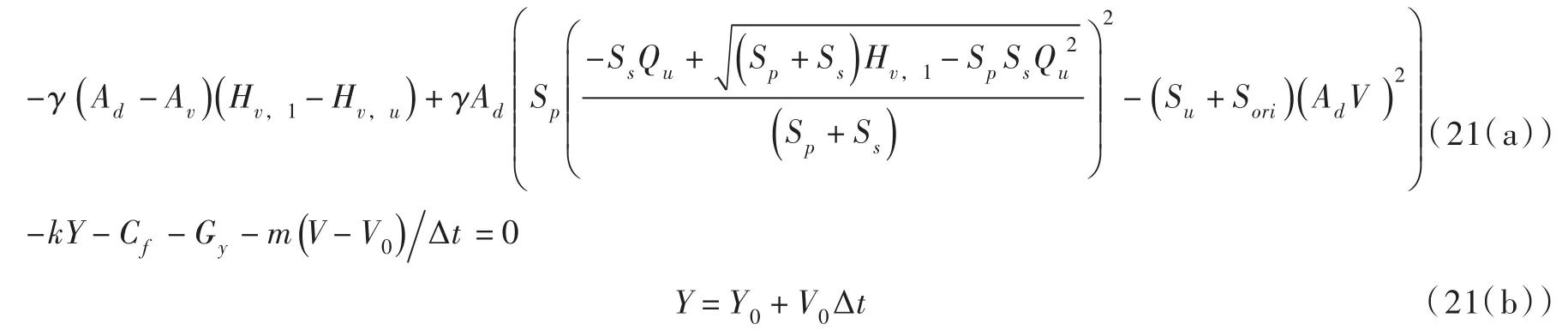
式中:Δt=t-t0为计算时间步长,s;下标“0”表示时刻t0。初始条件是:t0=0,V=V0,Y=Y0。当t0=0时刻主阀完全关闭时,V0=0,Y0=Ymin(主阀完全关闭时弹簧的压缩量)。在计算的过程中,Y和V是t的未知量,其它参数为已知量。
4 主阀关闭运动方程的解析
当把式(15)微分用一阶数值差分近视,则式(15)可改写为:
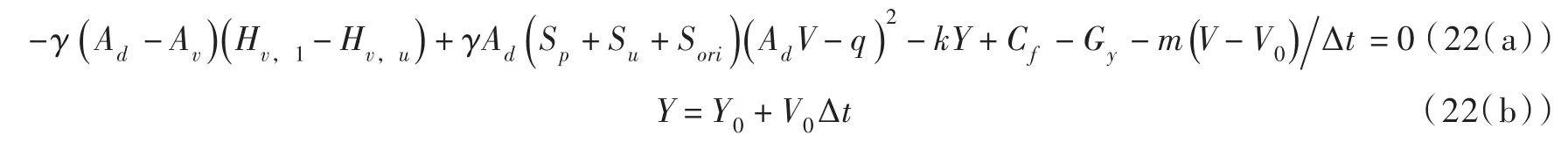
初始条件是:t0=0,V=V0,Y=Y0。当t0=0时刻主阀完全开启时,V0=0,Y0=Ymax(主阀完全开启时弹簧的压缩量)。采用数值计算方法求解式(22)可算出主阀行程、速度与时间的关系。
4.1 活塞渗漏流量为了防止泄压阀主阀关闭产生过高的水击压力及频繁的压力波动,通常采用主阀缓慢关闭的方式,运动部件的惯性力可以忽略不计,这时,式(22(a))可简化为:
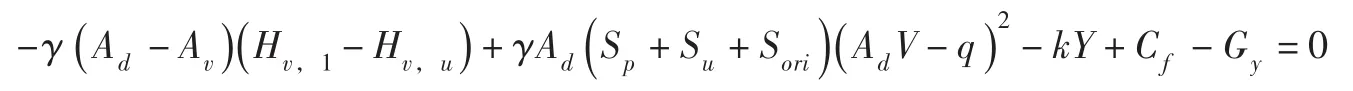
求解得:
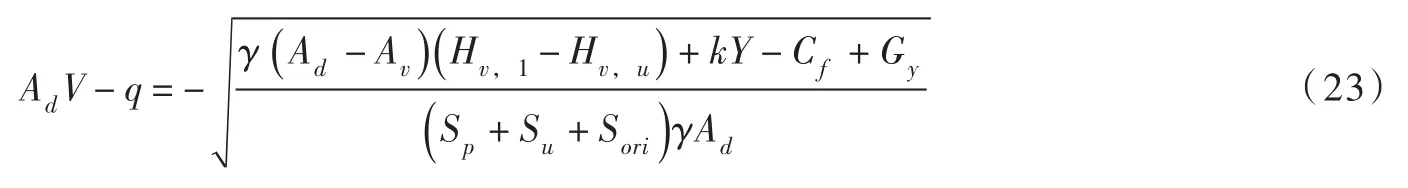
式中负号表示主阀瓣运动方向与Y方向相反。
把式(23)代入式(14)可得:
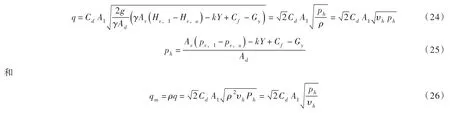
式中:Ph为作用于活塞上腔的绝对压力,Pa;pv,1=γHv,1;pv,u=γHv,u;qm为活塞渗漏质量流量,kg/s;υh=1ρ,液体在Ph下的比容,m3/kg,即密度的倒数。当压力1.6 MPa<Ph<6 MPa时,0.00 116 m3/kg<υh<0.00 131 m3/kg[12]。
《实用阀门设计手册》推荐的活塞环渗漏计算公式[12]是:

式中:

式中:qmf为活塞渗漏质量流量,kg/s;kv=0.5,渗漏流量系数。
当令渗漏流量系数:

则式(26)可改写为:
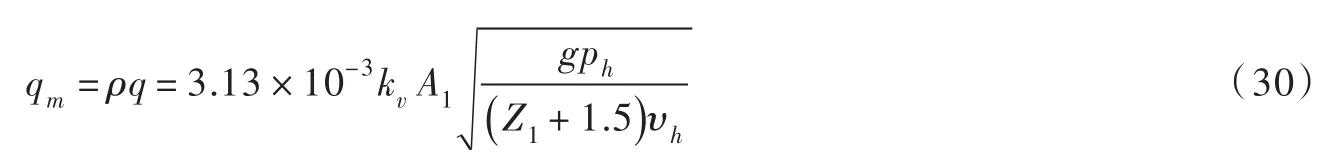
比较式(27)中和式(30)中ph,前者比后者多了一项pv,u,即主阀瓣上面(背面)压强,造成这一差异的原因可能是两种活塞式泄压阀结构形式不同或者笔误引起的。因此,对于图1先导活塞式泄压阀,建议采用式(30)计算液体的质量流量。
把式(29)代入式(24)可得渗漏流量计算公式:

4.2 减小水压变化对主阀关闭影响的方法式(23)可改写为:
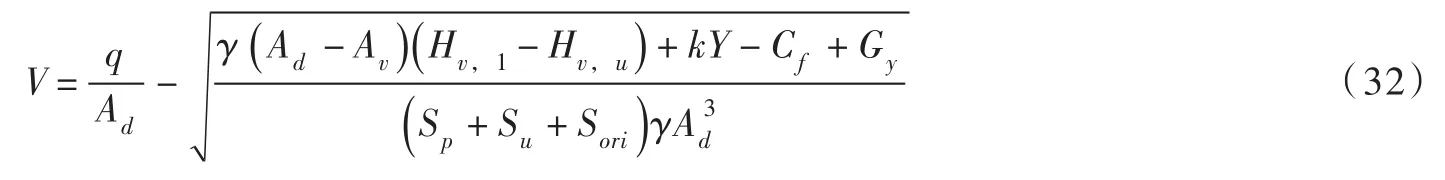
与式(22(b))和输水系统水击过程联立求解可得速度V和行程Y随时间的变化过程。
由于Hv,1>Hv,u,并且在阀门设计中Ad≥Av,所以,从式(32)可得主阀能够正常关闭(V<0)的充分必要条件:
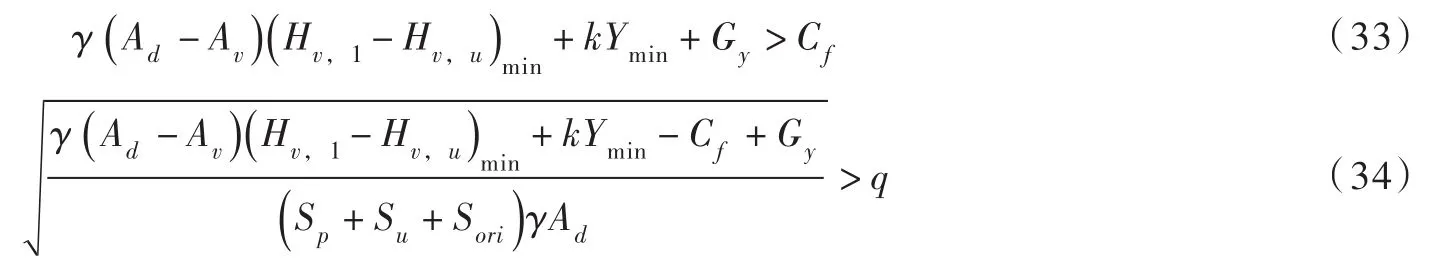
在摩阻力Cf已定的条件下,在正常渗漏的范围内,通过调整弹簧系数、活塞和主阀瓣直径,上述条件总是可以满足的。
当式(33)和式(34)同时满足时,从式(32)可得下述结论:
(1)活塞渗漏的存在会减缓主阀关闭的速度;
(2)当Ad≠Av,则主阀关闭速度受主阀瓣面上的水压差Av,1-Hv,u>0影响。当活塞直径大于主阀瓣直径,即Ad>Av,则水压差Av,1-Hv,u会加快主阀关闭的速度,可能导致产生较大的关阀水锤,优点是主阀完全关闭后密封力大,密封好;当Ad<Av,则Av,1-Hv,u会减缓主阀关闭的速度,甚至无法关闭。当Ad=Av,则主阀关闭速度不受主阀瓣面上的水压差Av,1-Hv,u变化的影响。
(3)主阀弹簧力、重力是主阀关闭的驱动力,而摩阻力虽然有减小关闭速度的作用,但是可能导致无法关闭。
(4)当针阀开度趋于零时,则Sp→∞,V→0;当缓冲孔孔径趋于零时,Sori→∞,V→0;因此,调节针阀行程和缓冲孔孔径中任一个都可调整主阀关闭速度。换句话说,缓冲孔减缓主阀关闭速度的作用可以通过减小针阀开度来代替,这时缓冲孔起着连通孔的作用。
《实用阀门设计手册》[12]对传统活塞式泄压阀(减压阀)建议取Dd=1.5DT,即Ad=2.25AT>Av,其中:DT为活塞进口过水断面直径,AT为活塞进口过水断面面积。显然,采用手册推荐设计,条件式(33)和(34)总是能够满足的,但是,由于主阀关闭速度受水压变化影响较大,关闭速度的控制(调试)非常困难。
令Ymin为主阀完全关闭时弹簧的压缩量,m,如果在设计的过程中,当下述条件满足:

则可取Ad=Av,即活塞直径Dd等于主阀瓣直径Dv,这时式(32)简化为:

在一般情况下,|V|≫qAd,所以,当Ad=Av时,作用在活塞和主阀瓣上的水压力相互抵消,泄压阀主阀的关闭速度基本不受水压变化的影响,目前,已经有些先导活塞式泄压阀在设计中采用了Dd=Dv或者Ad=Av。
当设计Ad=Av时,主阀瓣密封需要的压力可通过主阀结构设计解决,因为,主阀瓣面积Av总是大于主阀进水口面积AT,当阀门完全关闭时,通过上腔水压施加在主阀密封上的水压力为。例如,当主阀瓣直径Dv=0.16 m、主阀进水口直径DT=0.15 m、主阀进口水压Hv,1=10 m时,则,并且随主阀进口水压Hv,1的增加,密封挤压力会成正比增加。换句话说,在Ad=Av的条件下,可适当增大主阀瓣面积Av来满足主阀瓣密封压力的要求。
4.3 主阀关闭行程和速度与时间的关系在一般情况下,活塞渗漏流量,可忽略不计。当Ad=Av时,式(36)可简化为:

式中:
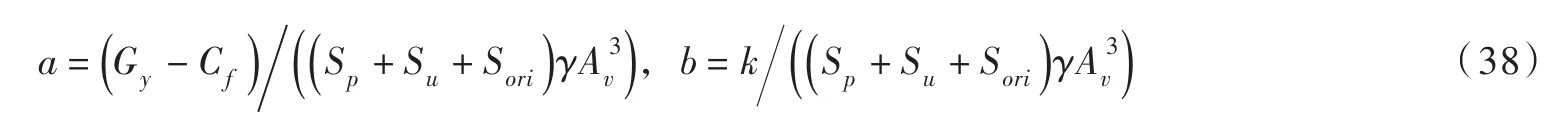
在泄压阀设计时,主阀瓣的最大开启高度(开度)(Ymax-Ymin)≥0.25D,其中:Ymax为主阀最大行程,m;Dv为主阀瓣直径,m。
求解式(37)微分方程得:

对式(39)求导得主阀关闭速度:

观察式(39)和式(40),可得下述结论:
(1)主阀关闭行程(开度)是时间的二次函数;
(2)主阀关闭速度与时间成线性关系,速度绝对值随时间的增加而减小,即先快后慢。
当令主阀行程完全关闭的时间为Tc及主阀完全关闭时刻的速度为Vc,则由式(39)和(40)得:
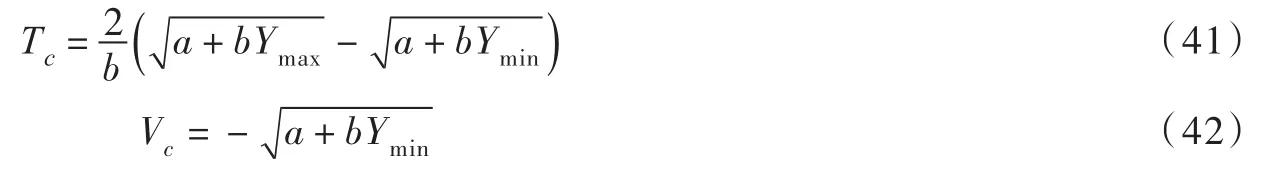
当条件式(35)满足时,则式(39)—式(42)成立。
5 活塞式泄压阀设计算例
泄压阀水力设计的要求是:
(1)主阀开启迅速,时间短,以减小管道水击压力升高;(2)主阀关闭缓慢,以防止关闭过快产生关阀水锤;(3)为了防止泄压阀开启过快导致下腔内液体汽化,缓冲孔水头损失

式中:hori为缓冲孔水头损失,m;海平面水的汽化压头约为8 m,∇为泄压阀使用地点的海拔高程,m。
5.1 泄压阀水力学参数以图1为例,液压传动系统进水管、上腔管、泄水管一般采用铜管,属于光滑管,且一般直径较小,流动处于紊流过渡区,沿程阻力系数f与雷诺数有关,即与流量有关,不过,考虑到Sp和Su中局部水头损失占比较大,可近似取f为常数,对于泄水管也采用同样方法处理。
液压传动系统管道进/出口、弯头、交汇点、滤网、针阀、球阀(检修阀)、导阀止回阀及缓冲孔产生局部水头损失。进水管进口可视为管道突缩,阻力系数ζin=0.2~0.5;主阀开启时,上腔管进口(与上腔连接处)ζin=0.2~0.5。泄水管出口和上腔管进口(与上腔连接处)可视为管道突扩,阻力系数ζout=1.0。管道90°弯头阻力系数ζw=0.137~0.291,光滑管急转弯头ζjw=1.1[11]。Y型滤网滤芯一般用不锈钢制成,滤孔总面积是入口管道截面积的3~5倍,阻力系数ζy=1.5~3。导阀止回阀阻力系数ζc与流道结构和开度有关,开度越小,ζc越大,全开时ζc=3~7;针阀作为微调阀,可以调节进水管的流量,全开时阻力系数ζn=4.8~7.2[11]。缓冲孔为孔板出流,其局部阻力系数可视为管道突扩和突缩的组合,ζori≈1.5。球阀作为检修阀,正常工作时保持全开,水头损失可忽略不计。在主阀关闭时,上腔管进口可视为急转弯头。图1交汇点A局部水头损失情况复杂,与分流比、流态、相互角度有关(华少增,杨学宁)[13],但与止回阀相比较小,可忽略不计。
在下面的计算中,进水管局部阻力系数(进口+1个90°弯头+针阀+滤网)ζp=0.5+0.291+6.0+2.0=8.791;泄水管局部阻力系数(导阀止回阀+出口)ζs=3+1=4;主阀关闭时,上腔管局部阻力系数(进口1个急转弯头+出口)ζuc=1.1+1=2.1;主阀开启时,上腔管局部阻力系数ζuo=0.5。
5.2 基础数据水击泄压阀公称直径一般小于1000 mm,本例取泄压阀进口过水直径DT=0.3 m,主阀瓣直径Dv=0.32 m,活塞直径Dd=Dv。主阀瓣质量与工作压力和材料的许用弯曲应力有关,可参考专著[11]止回阀阀瓣厚度计算,计算中取。当取活塞质量与主阀瓣相同时,主阀运动部件质量m≈2mv。Y方向和水平面的夹角取60°,Gy=gmsin60°。取活塞环数Z1=3;摩擦系数fm=0.2;活塞环径向厚度;活塞环的宽度b=0.4 h;活塞环自由开口间隙s=3 h;活塞环自由状态与工作状态间隙之差Δ=s-δ,其中活塞环工作状态开口间隙δ=0.25×10-3m;活塞环弹性模量E=1011Pa。取以消除活塞环摩阻力的影响。
5.3 泄压阀数值试验结果当Dd=Dv时,作用在活塞和主阀瓣上的水压作用相互抵消,不影响泄压阀关闭过程,但影响泄压阀的开启过程。由于水压的变化受整个输送系统影响,为便于下面的计算分析,如果不作说明,则在泄压阀数值试验的过程中,假设主阀开启过程中进口水压保持在导阀开启的临界水压Hcri,且∇=0。
表1列出了主阀瓣Dv=0.32 m时7组泄压阀数值试验的计算参数及结果一览表,包括:主阀开启的临界水压;主阀弹簧系数,最大行程和最小行程;液压传动系统的管径、管长、沿程阻力系数和局部阻力系数、阻抗系数等水力学参数;工作压力,运动部件质量和重力。计算结果是:主阀完全关闭时间Tc(数值计算和解析式计算),主阀完全开启的时间Top,主阀开启过程中缓冲孔最大水头损失hori,max,活塞环摩阻力,主阀关闭过程中液压传动系统进水管的最小流量、活塞最大渗漏流量、最大雷诺数和最小雷诺数。在数值计算主阀完全关闭时间Tc的过程中考虑了运动部件的惯性力及活塞渗漏流量的影响。
分析表1计算结果可得下述结论:
(1)采用解析公式(41)计算主阀完全关闭的时间具有很高的准确性。考虑运动部件惯性力和活塞泄漏时,数值计算的主阀完全关闭时间Tc2范围是24.6 s~49.7 s;当运动部件惯性力和活塞泄漏忽略不计时,解析公式(41)计算的Tc1范围是24.20 s~48.50 s,(Tc2-Tc1)/Tc1<3%。活塞最大渗漏流量qmin范围是0.033×10-4~0.057×10-4m3/s,对应进水管最小流量Qpmin范围1.103×10-4~2.365×10-4m3/s,。
(2)泄压阀运动部件的质量随水压的增加而增加,这是由主阀瓣和活塞的强度要求确定的。当工作压力从2 MPa增加到6 MPa,运动部件质量从49.71 kg增加到85.17 kg,见分组1—3(见表1)。
(3)活塞环摩阻力与运动部件重力在数量级上相同,分析时必须考虑,但是可以通过主阀弹簧抵消它的作用,例如取主阀完全关闭时的压缩量。
(4)当主阀完全关闭时间在24 s~50 s范围内,主阀关闭时进水管的最大和最小雷诺数Re=104~2.5×104。
(5)减小针阀开度或进水管直径,可以减小主阀关闭速度,增加关闭时间,但对开启过程的影响可忽略不计。观察分组3和4,当减小进水管针阀开度,使进水管局部阻力系数由全开的8.791增加到16,则主阀完全关闭时间Tc1从29.7 s增加到38.9 s;而主阀完全开启时间Top分别为0.57 s和0.56 s,变化微小。
(6)增加泄水管直径,可以提高主阀开启速度,减少开启时间。观察分组4和5,当泄水管直径由0.015 m增加到0.025 m,则主阀完全开启时间Top从1.48 s减小到0.56 s。
(7)增加上腔管直径,可以减少主阀关闭与主阀开启时间。观察分组5和6,当上腔管直径由0.015 m增加到0.025 m,则主阀完全关闭时间Tc1从41.2 s减小到38.9 s;而主阀完全开启时间Top从1.72 s减小到 1.48 s。
(8)减小缓冲孔孔径,可以减小主阀关闭速度,增加关闭时间,但是过小的缓冲孔孔径不仅减小主阀开启速度,增加开启时间,而且活塞下腔可能发生液体汽化现象。观察分组6和7,当缓冲孔孔径由0.03 m减小到0.01 m,则主阀完全关闭时间Tc1从41.21 s增加到48.50 s,主阀完全开启时间Top从1.72 s增加到2.81,但是主阀开启缓冲孔最大水头损失从2.2 m水头增加到65.6 m水头,显然,在主阀瓣背水面(图1主阀瓣上面)压头较低的情况下,活塞下腔会发生液体汽化现象。
(9)主阀启闭Y-t和V-t行程曲线几乎是线性的,见图2和3所示。
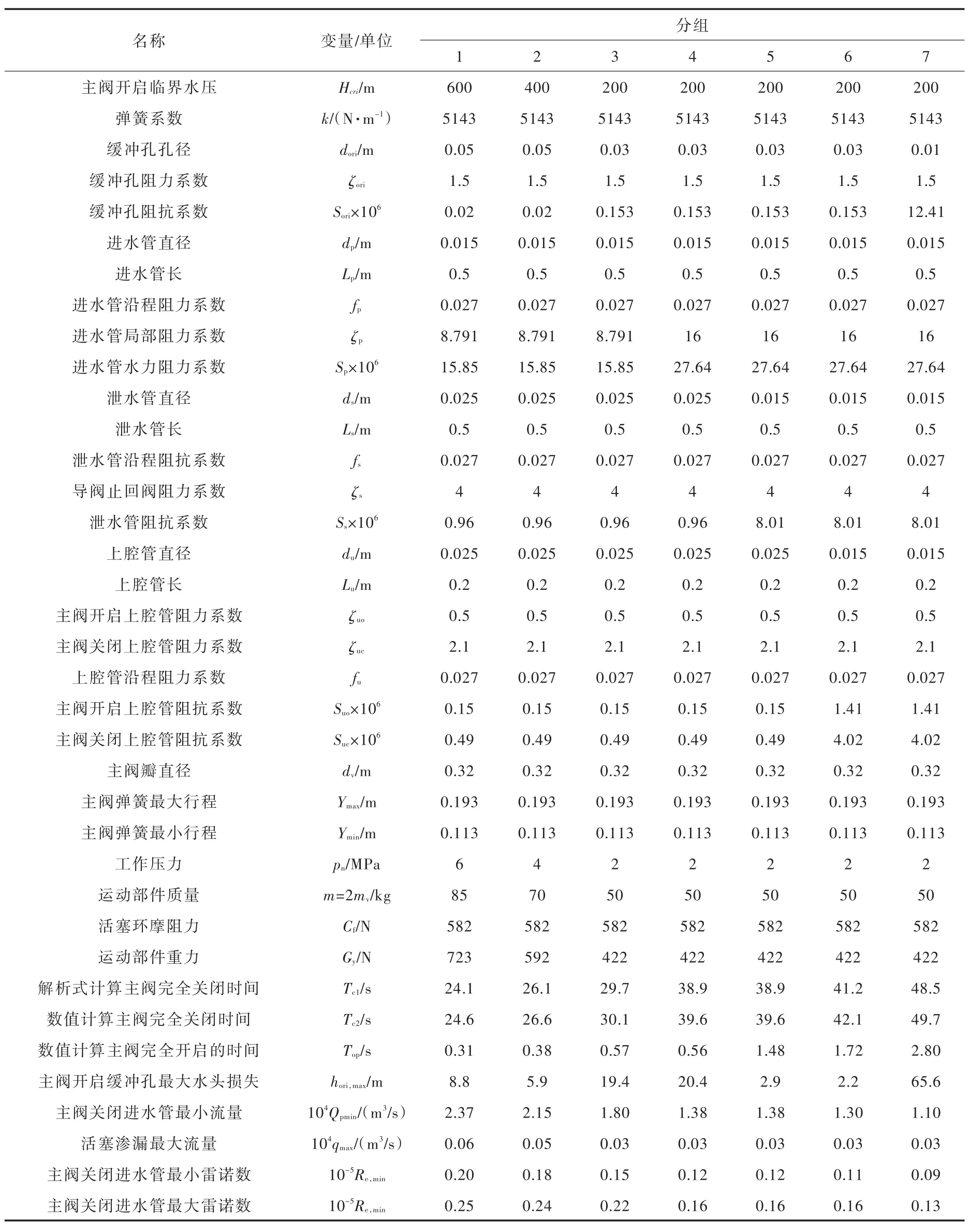
表1 活塞式泄压阀计算参数及结果
6 结论
导阀止回阀行程通常很小(小于1 cm),开启和关闭的时间过程可视为瞬间完成,因此可视导阀为0-1系统,只存在两种状态:完全关闭状态和完全开启状态。

图2 泄压阀开启Y-t和V-t过程(1—分组1参数;2—分组6参数)
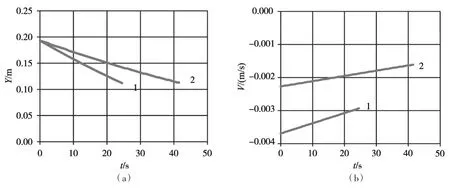
图3 泄压阀关闭Y-t和V-t过程(1—分组1参数;2—分组6参数)
本文系统地考虑了影响先导活塞式泄压阀运动的各方面因素,包括水压力、运动部件的重力、弹簧力、活塞环摩阻力和渗漏等,基于结构运动力学和水力学原理,得到了主阀启闭速度与液压传动系统流量的函数关系,建立了主阀启闭过程速度和行程与时间的数学模型,然后,通过主阀关闭运动方程的解析,修正了现有活塞渗漏流量的计算公式,提出了合理选择活塞直径与主阀瓣直径以减小水压变化对关闭过程影响的方法,然后解析得出主阀关闭速度、行程、关闭时间的计算公式。
通过研究,得到下述结论:(1)当活塞直径大于主阀瓣直径,即Ad>Av,则水压会加快主阀关闭的速度,可能导致产生较大的关阀水锤;(2)当在设计的过程中取主阀完全关闭的弹簧压缩量,则可取Ad=Av,这时作用在活塞和主阀瓣上的水压力相互抵消,主阀关闭过程几乎不受水压变化的影响,然后,通过适当增加主阀瓣直径来解决主阀瓣密封需要的水压力问题;(3)当Ad=Av,主阀关闭行程(开度)是时间的二次函数,速度与时间成线性关系,关闭过程先快后慢;(4)活塞渗漏的存在会减缓主阀关闭的速度。
通过Ad=Av的7种实例的计算分析,得到下述结论:(1)在计算分析主阀关闭规律时,运动部件惯性力和活塞泄漏可忽略不计,采用解析公式计算主阀行程和完全关闭的时间具有很高的准确性;
(2)主阀关闭时进水管的最大和最小雷诺数Re=104~2.5×104;(3)减小针阀开度或者进水管直径,可以减少主阀关闭时间,但对开启过程的影响可忽略不计;增加上腔管和泄水管的直径,可提高主阀开启速度;缓冲孔减缓主阀关闭速度的作用可由调整针阀开度代替,因此,可适当增加缓冲孔孔径,以避免主阀开启时活塞下腔发生液体汽化现象;(4)主阀启闭Y-t和V-t行程曲线近似线性。需要说明的是,本文先导活塞式泄压阀主阀运动规律也适用于压力波动预止阀,因为两者的主要差别是后者比前者多了1个低压导阀。
