一种高速无人机下行链路信道估计方法

张延洞，郭立民，禹永植，陈斌杰

(1.哈尔滨工程大学，黑龙江 哈尔滨 150001；2.北京遥感设备研究所，北京 100854)

0 引 言

在高速无人机下行数据链路中，地空无线信道是复杂和不可预测的，电波除直射外还有反射、散射以及绕射等，路径的长短不同，导致到达时间不同，进而引起多径效应，此外无人机的高速移动又会引起严重的多普勒效应。这将导致信道响应出现频率及时间选择性衰落[1]。正交频分复用技术(OFDM)是一种具有灵活带宽、抗衰落及抗码间干扰能力强等优点的通信技术[2]，因此非常适合高速无人机下行数据链路。OFDM信号在经过地空无线信道后，会出现失真的现象，一般为幅度和相位的变化，为了得到发端的数据，就必须要对信道特性进行估计并对信道产生的影响进行补偿，因此信道估计受到了广泛的关注[3]。

信道估计算法大致可分为3类：盲信道估计、半盲信道估计以及非盲信道估计[4]。其中，文献[5]对盲信道估计进行了整体介绍，该类算法无需在发端发送已知信息，不占用带宽，但缺点是运算量较大，运算时间长，不利于在实际工程中实现。而基于已知导频处进行信道估计的几种方法中，文献[6]中的最小二乘(LS)估计的主要特点是简单、复杂度低,易于设计和实现,但其缺点在于未考虑噪声的影响，低信噪比下性能较差。相比于LS算法，文献[7]中的最小均方误差(MMSE)算法引入了信道的特性和噪声的影响，提升了性能，缺点是算法复杂且实际应用中噪声的统计特性无法获得，实现起来较为困难。文献[8]线性最小均方误差(LMMSE)相较于MMSE，降低了计算的复杂度，但仍然高于LS算法。

本文首先对无人机地空信道的特点进行了介绍，并根据特点构建了地空信道模型，紧接着构建了基于OFDM的下行数据传输链路。针对信道估计技术，当前许多算法复杂度过高，不易工程实现，本文通过对LS信道估计算法和卡尔曼算法进行研究，立足实际，提出一种联合算法来提高格状导频下的信道估计性能。该方法有效结合了LS估计算法与卡尔曼估计算法的优点，通过结合卡尔曼的方法提升了LS估计算法在格状导频下的估计准确性；相较于只能在梳状导频下进行的卡尔曼估计算法，能够大幅降低导频使用数量，从而提高带宽利用率，具有一定的实际应用价值。

1 系统模型

1.1 地空信道模型

在地面站与空中的无人机进行无线通信时，信道模型主要有2个特点：一是多径效应严重；二是多普勒频移严重[9]。图1给出了无人机地空通信的示意图。

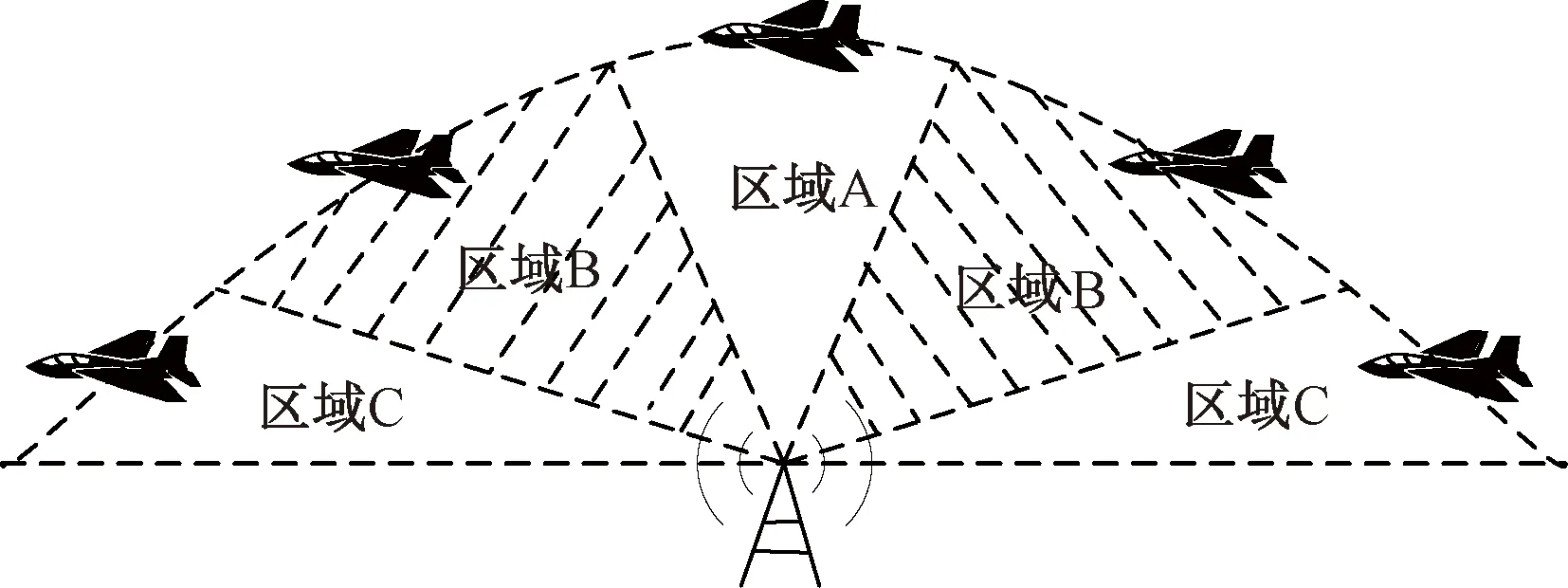
图1 地空通信示意图

从图1可以看到，无人机与地面站之间的信道特性与仰角大小、相对位置关系有着密切的关系。根据相对位置和仰角的不同，可以大致分为3种区域。

其中当空中飞行器终端位于地面站的正上方位置时，即图1中区域A，为高仰角区域，此时飞行器终端径向速度较小，多普勒频移小，且遮挡较少，可以近似视为高斯信道。随着无人机与地面站之间距离的增大，仰角逐渐变小，各种地面障碍物的影响越来越大，造成严重的多径效应，如图1区域B所示。当进入到图1区域C中时，无人机与地面站之间的直射分量几乎被各种障碍物遮挡，传输可能会导致中断。因此本文重点研究图1区域B中的地空无线信道情况。

多径效应要考虑的路径主要为无人机与地面站之间的直射路径、高山等障碍物引起的反射路径以及散射路径，如图2所示。

图2 区域B的地空信道路径图

因此，可以用三径模型来描述地空通信的实际信道，其中直射路径为主径，服从莱斯分布，反射路径与散射路径等形成的多径服从瑞利分布。

除了多径效应外，无人机飞行速度较高，因此还会带来多普勒效应，如图3所示。

图3 多普勒频移示意图

多普勒频移与无人机的运动速度以及载波波长有关：

(1)

式中:fc为系统载波中心频率；c为光速。

无人机的最大飞行速度一般不超过300 m/s，载波中心频率为2 GHz，当θ=0时，cosθ有最大值，此时多普勒频移最大：

(2)

综上所述，本文地空信道的主要参数如表1所示。

表1 地空信道参数设置

按照表1的参数设置，对地空信道进行建模，仿真结果如图4所示。

图4 地空信道仿真图

图4中实线表示主径，其功率要大于另外两径，服从莱斯衰落，虚线和点划线分别表示反射和散射子径，为瑞利衰落。

1.2 OFDM传输模型

图1为OFDM通信系统的结构框图，主要包括映射、串并转换、导频插入、反快速傅里叶变换(IFFT)运算、插入CP等模块。其中IFFT为核心模块，也是OFDM调制过程，通过IFFT把比特数据调制到不同的正交子载波上，并直接将一个周期内的叠加结果计算出来。经IFFT变换得到的时域信号x(n)可以表示为：

(3)

式中:X(k)表示OFDM的频域信号；N为子载波个数。

调制后的信号需插入循环前缀充当保护间隔，之后信号经并串转换，转回串行数据流，最后进行发射。

图5 OFDM系统框图

接收端的结构与发送端相反，首先去除循环前缀，得到的信号为：

y(n)=x(n)*h(n)+w(n),n=0,1,…,N-1

(4)

式中：*表示卷积；h(n)为信道响应；w(n)为噪声。

对y(n)做快速傅里叶变换(FFT)变换，得到：

Y(k) =X(k)H(k)+W(k)

(5)

经信道估计后，进行解映射，得到所传输的信息。

导频插入的结构有3种：块状、梳状和格状。其中，块状导频时域离散，频域连续，适合多径信道；梳状导频频域离散，时域连续，适合多普勒信道；而格状导频时频域皆为离散，导频使用数量下降，本文中多普勒和多径都较为严重，因此需要兼顾时频2个方向，采用格状导频结构。

2 信道估计

2.1 LS信道估计算法

接收端信号可以表示为：

Y=XH+W

(6)

式中：X表示已知导频序列；Y表示导频位置接收信号；H表示导频位置的信道频率响应；W为信道中的噪声。

LS的估计准则是误差的平方和最小，则代价函数J为：

YHY-YHHY-HHXHY+HHXH

(7)

对式(7)求偏导，得到：

(8)

令式(8)等于0，即代价函数最低，求得的信道估计结果为；

(9)

2.2 卡尔曼估计算法

卡尔曼( Kalman )最优估计技术是由卡尔曼与布西合作发展形成的一套最优估计理论,是一种基于时域最优估计的方法[10],它通过采用状态空间的最优估计方法对信号进行描述，并将信号过程视作白噪声下的线性系统输出，从观测量中估计出所需要的信号。

假设用以下状态空间模型来构造：

H(k)=ΦH(k-1)+W(k)

(10)

Y(k)=H(k)X(k)+V(k)

(11)

式中：k为离散时间，系统在时刻k的状态为H(k)；Y(k)为相应时刻的观测值；W(k)为引入的白噪声；V(k)为观测带来的噪声[11-12]。

式(10)为状态方程，式(11)为观测方程，Φ为状态转移矩阵。递推Kalman估计如下：

状态一步预测：

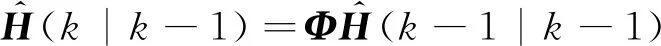
(12)

状态更新:

(13)

滤波增益矩阵：

K(k)=P(k|k-1)XH[XP(k|k-1)XH+R]-1

(14)

一次预测协方差阵：

P(k|k-1)=ΦP(k-1|k-1)ΦT+Q

(15)

协方差阵更新：

P(k|k)=[In-K(k)X]P(k|k-1)

(16)

(17)

W(k)和V(k)是均值为零、方差阵各为Q和R的不相关白噪声。初始状态X(0)不相关于W(k)和V(k)。

卡尔曼算法采用递推的形式,无需存储所有时刻历史数据,只需根据前一时刻的估计值和当前时刻的测量值,即可准确计算得出新的估计值[13]。

2.3 LS-KF联合估计算法

LS算法的缺点在于忽略了噪声的影响，噪声大时，其性能较差；而卡尔曼估计方法需要保证导频在时间域是连续的，所需导频数量较多，且估计误差会随着时间不断累积，导致性能下降。本文结合二者优势，且对劣势互相弥补，提出了LS-KF联合估计算法，首先是插入格状导频，可以兼顾对时域、频域2个方向的信道估计，并减少导频使用量；然后利用LS估计方法得到离散导频位置处的粗信道响应估计值；紧接着进行时域插值，将时域离散转变为时域连续；进而采用卡尔曼算法对其进行二次估计，进一步优化估计性能；最后利用优化后的时域方向估计值进行频域方向插值，完成整个信道估计。

该方法的具体步骤是：

(1) 对导频位置的信号进行提取，得到YP。

(5) 利用步骤(4)中优化后的时域方向的估计值进行频域方向的插值拟合。

3 仿真分析

在仿真实验中，通过Matlab对LS-KF联合算法进行的仿真，信道2.1中建立的模型，并加入不同的多普勒频移，具体参数设置如表2所示。为了验证联合算法的有效性，在仿真实验中，通过设置不同的导频插入方式和不同的多普勒频移，与LS算法、卡尔曼估计算法进行了对比。

表2 仿真参数设置

图6为在多普勒频移Δf=500 Hz情况下，4种算法在不同信噪比条件下的误码率变化趋势。从图6可以发现,LS算法因其在计算过程中忽略了噪声因素的影响，总体性能较差，尤其是在格状导频下，性能最差。梳状导频下LS估计性能有所提升，但代价是增加了导频使用数量。卡尔曼估计由于其递推算法会导致误差累积，在信噪比较低时相比LS算法有优势，但在信噪比较高时，优势不大。

从图6中可以看出，在Δf=500 Hz、系统误码率为10-4时，本文提出的LS-KF联合估计算法在格状导频下与LS算法相比，有2 dB左右的性能提升；与梳状导频下的LS算法相比，在导频使用数量下降了60%的同时，有1 dB左右的性能提升。与卡尔曼估计算法相比，性能较为接近，但导频使用数量下降60%。

图6 Δf=500 Hz时误码率性能比较

在多普勒频移增大为Δf=2 kHz后，如图7所示，4种算法的性能均有所下降。在系统误码率为10-3时，本文算法在格状导频下与LS算法相比有3 dB左右的性能提升；与梳状导频下的LS算法相比，在导频使用数量下降了60%的同时，有2 dB左右的性能提升；与卡尔曼估计算法相比，性能提升1 dB左右，但导频使用数量下降了60%。与Δf=500 Hz时的性能提升相比，本文算法在大多普勒频移的条件下，性能提升更大。

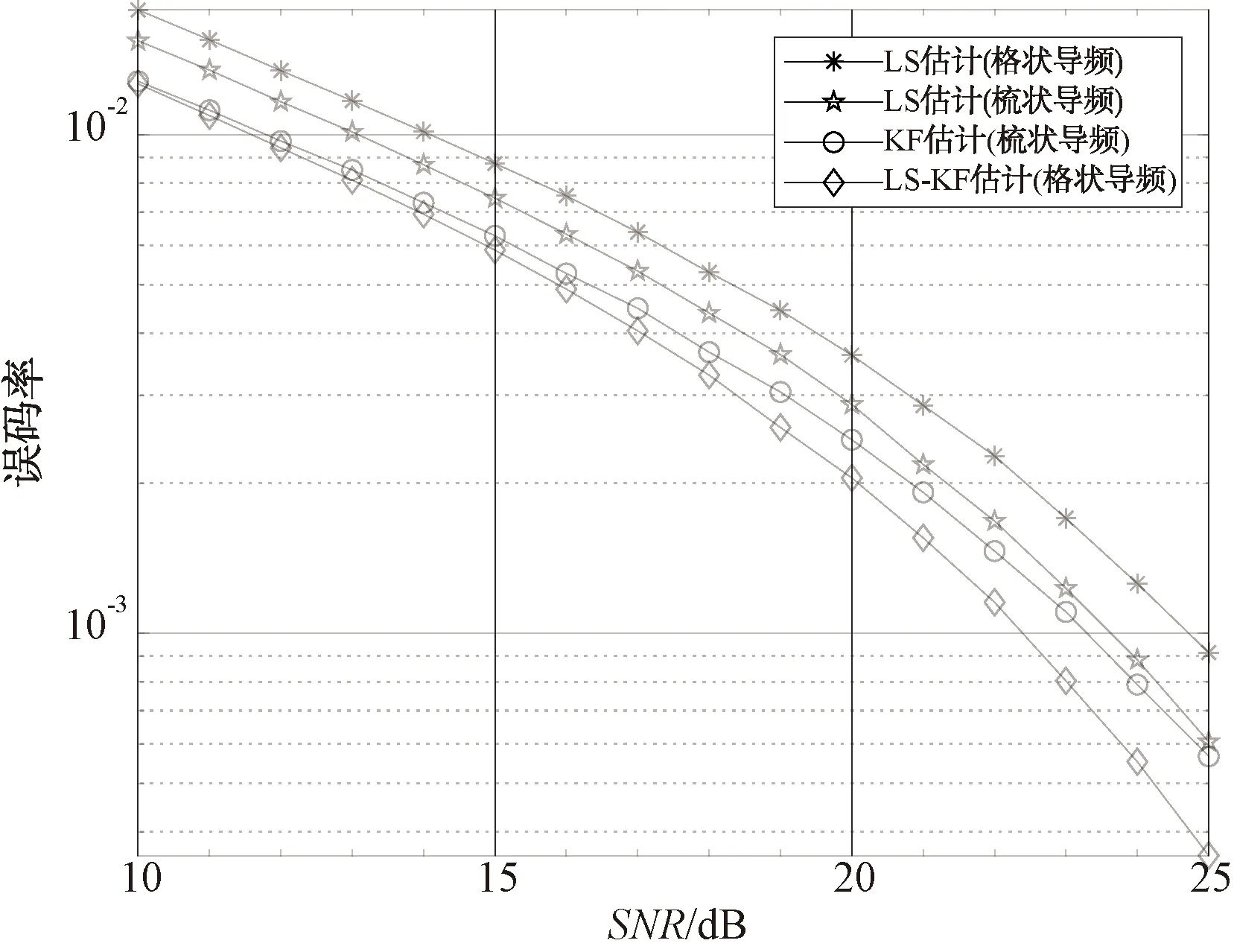
图7 Δf=2 kHz时误码率性能比较

图8为Δf=500 Hz时，4种算法在不同信噪比下估计的均方误差仿真曲线图。在相同信噪比下，梳状导频下的LS算法比格状导频下的LS算法估计精度有2倍左右的提升；本文提出的算法相比梳状导频下的LS算法估计精度又有4倍左右的提升。

图8 4种算法均方误差性能比较

4 结束语

为了解决高速无人机下行数据传输中，地空信道多径效应以及多普勒效应严重导致系统性能下降的问题，本文首先建立了高速无人机地空信道的模型，提出了一种格状导频下的LS-KF联合估计算法，并与现有的传统算法进行了仿真对比，结果表明：该方法解决了格状导频因时域离散而无法进行卡尔曼估计的问题，并相较于时域连续的梳状导频下的卡尔曼估计算法，性能提升约1 dB左右，但导频使用数量下降60%。相较于传统LS算法，导频使用数量相同，性能有2～3 dB的提升。